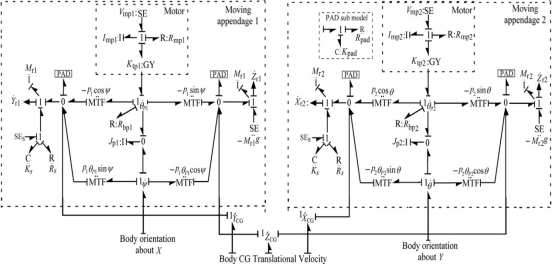
图3.移动附件装置键合图模型

小齿轮，采用小公里和当量的假设。(5)给出了姿态控制器电机电压输入的控制律：

其中KP1、KV1和Ki1分别是控制器的比例增益、导数增益和积分增益。

为了控制Y轴的身体方向θ，使用了另一个移动附件。它的机架在x方向运动，在y方向没有运动。以获得其控制电压INP的控制律对于小齿轮电机和位置，X方向和Z方向上的速度方程可以像上面讨论的那样导出。

四足机器人被认为是六自由度刚体.。它的转动动力学可以用欧拉方程给出，它的体-固定轴(xyz-轴)与原则对齐。铝轴：

其中，nx，ny和nz代表作用在物体上的矩，ixx，iyy和izz表示主要的惯性矩，ωx，ωy和ωz表示角速度，下标表示角速度。用斧头。机架的运动只改变了两个轴(x和y)的身体方向。不需要控制第三轴的旋转。

移动附件装置的键合图模型如图3所示模型的左、右两部分表示在虚线矩形内，处理机架在体固定X和Y dir中的运动。

模型左边部分的构造在这里详细说明。下齿条的体固定X运动由小齿轮1的旋转决定。小齿轮1相对于TH的旋转角度E体固定X轴为θp1，其取向为小齿轮的总角速度为θ·p1ψ·，在转动惯量i：jp1为0的交界处模拟。

连在一起。同时，0-接点还模拟了车身上的反应力矩.。直流电动机是在一个1-连接(指示共同的电流)的电源电压(SE：vmp1)上建模的。、电枢电感(I：Imp1)、阻尼(R：Rmp1)和机电耦合(GY：Ktp 1)。机电联轴器产生与电枢电流成正比的转矩作为一个感应电动势（EMF）成正比的小齿轮速度，比例常数被称为电机特性常数。齿轮减速电机的传动比为包括在电机特性常数的定义中。

分别是。请注意，没有显式显示调制信号以保持图形的清晰度。上述三种流动的结果在一个1-节点上建模。连接机架I：MR1惯性的离子。为了限制移动附属物离开顶部的运动，一个停止被建模为一个切换的刚性弹簧阻尼器系统，其中ks回购。esents弹簧常数和Rs表示停止的阻尼Coeffi。由于停止反作用力只能在附属物与停止之间的接触中出现，因此，SE是一种切换的努力。RCE是用于抵消由于机架覆盖的长度不受阻碍而产生的不正确的努力。同样地，用方程给出的运动学关系式。(4)通过在0-节点处添加三个流动变量来模拟。从1Z·cg键中直接键的离子，指示机器人身体在Z方向上的速度，以及通过调制变压器mtf：−p1 sinψ的两个键。

MTF：−p1θpcosψ分别来自1·和1。上述三种流的结果流是1 θp1 ψ

在一个1节点建模，其中机架I：MR1的惯性和自重SE：−Mr1g是连接的。模型的传感器和输出以激活或信号键表示，即b。在它们的末尾有一个完整箭头的秒。

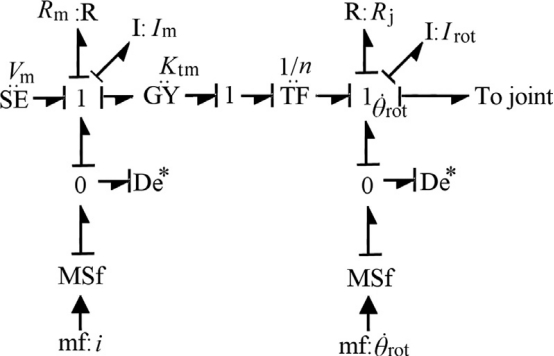
图4.腿部关节驱动器的DBG

衬垫元件&bra;14，17&ket;是刚性弹簧-阻尼系统，其在运动之间建立隐式约束，并且这里使用它来避免模型中的差异因果关系。

P值大AD刚度和阻尼参数以数值刚度为代价产生几乎理想的运动学耦合，即模拟时间。

同样，图的右边。3建立第二齿条和小齿轮布置模型。图中模型底部的五个开放端口。3表示三个线性速度和两个旋转速度。机器人本体的特性和这些被动端口将与机器人的模型进行接口。移动附属物的力和力矩信息被施加到机器人身上。通过这些港口。

3.容错控制

主动容错控制方法根据系统的故障情况采用不同的控制律。容错控制的被动方法是在pla中利用冗余硬件实现的。通过重新配置控制体系结构来实现故障部件的计算。在本文中，传感器冗余被用来估计丢失的测量。控制律(步态模式)也被改变利用ND冗余硬件(运动附件)对执行器故障进行容错控制。因此，所提出的方法是主动式和被动式容错控制的混合体。策略

为了实现容错控制，必须了解系统中各部件的健康状态。这需要对系统进行持续监视，以便在检测到时对于任何异常，都可以识别故障分量，并执行相应的容错步骤。

3.1.故障检测与隔离

安全临界系统可能在没有任何警告或症状的情况下失效。在这种情况下，必须不断监测和监督该系统。监督系统使用一套工具来操作。在有缺陷的情况下，也要保持健康。这一过程主要包括三项工作：监测系统的故障检测(警报或异常状态)，故障隔离以识别故障。组件和确定的根本原因，最后，作出的决策，以适应故障，如果可能的话。故障检测和隔离可以通过分析R以结构化的方式进行。涡流关系(ARRS)。ARR是一组已知过程变量^[11，12]之间的一组兼容性条件或约束。用实测数据评价ARR(约束有效性t)EST)被称为残差。理论上，在健康运行过程中，残差应为零。

为了导出四足机器人的ARRS，准备诊断结合图(DBG)。

在DBG中,将键合图模型中的传感器转换为对模型中，添加了一组剩余输出端口，并将模型分配为优选差分因果关系。图中DBG中已知的测量值。4电机电流i和小齿轮旋转。nθ·ROT，它通过两个调制流源施加于DBG模型上，作为已知信息。在这里，关节执行器(具有特征常数ktm的齿轮直流电动机)有一个gea。r还原比为1：n。注意，在键合图表示中，旋转器gy和变压器tf组合在一起，使旋转器和旋转器模数ktp(有进一步的下标1和2来表示mo)。Tor数)等于KtMn。努力源(SE：VM)、电阻(R：RM)和电感(I：IM)连接到一个表示公共流的1结，即电流I。论技工在另一个1-节点上，分别模拟了转子的极转动惯量(i：irot)、关节摩擦(R：rj)和机械系统其余部分的功率输出(用文本“to john”表示)。对于表示关节角速度的通用流，θ·ROT。

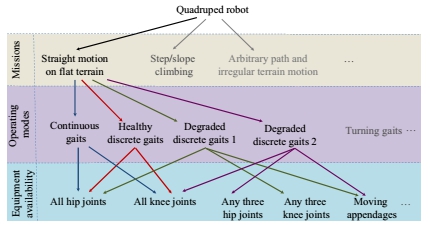
图5.操作模式和设备可用性图表扩展为直线运动任务和设备(这里只有执行器)可用性。

连接给出了模型中的两个ARRS。注意，ARRS的数量总是等于传感器的数量。从DBG衍生ARR的详细步骤可在^[6，22]中查阅。一个腿关节有两个ARRS，可以写成：

其中VM是电源电压，IM是电机电感，I是电枢电流，RM是电机电阻，ktm是电机常数，θ·ROT是角速度，RJ是关节摩擦，n齿轮传动比，转子惯量，τθ是静反作用力矩。在EQ中下标j.。(8)和(9)表示联合编号。四足动物有八个腿关节，所以总共16个AR。RS已形成。同样，用于姿态控制器执行机构的ARRS可以编写为：

(10)-(13)对应于姿态控制执行器1和2，其中Vmp1和Vmp2是电源电压，ip 1和ip2。

电枢电流是电枢电流，脉冲1和脉冲2是电机电感，Rmp1和Rmp2是电机电阻，Ktp 1和Ktp 2是电机常数，θp1和θp2是小齿轮的角速度。Rbp 1和Rbp 2是连接摩擦，n是齿轮比，jp 1和jp 2是小齿轮惯性。

ARRS的结构分析用于产生故障特征矩阵(FSM)，该故障特征矩阵是一个二进制矩阵，其示出了各个组件的参数对每个残差的贡献。

可监控的或可检测的故障必须影响至少一个残余。可隔离的故障影响唯一的残差集(称为故障特征)，它不同于受ot影响的残差集。她的缺点。在这种情况下，所有的电机故障有独特的非零故障特征和故障监控和隔离都可以。

在故障检测和隔离之后，必须根据设备的可用性来确定适合于完成所需任务的工作模式(OM)。一般来说，四足机器人需要执行许多任务，其中三项如图所示。5.。为了执行这些任务，它必须遵循一个适当的OM，可以根据现有的设备来决定。如图所示。5.直线运动可以使用四种可能的操作模式来执行，其中两种是为了机器人的健康状态，两种是针对被认为是锁定的关节故障，也称为退化模式。ES，即与系统的健康状态相比，其运动性能较差的运行模式。对于其他类型的任务，有许多其他的操作模式，它们是图中未显示。是选择OMS重要设备也是传感器，但他们都没有显示设备的可用性下保持清晰的图。

图中所示的组织。5只从健康执行器的可用性角度来解释，传感器的可用性也可以加以说明。这个机器人被认为是所有小腿关节都处于健康状态。

执行器（髋关节和膝关节）和传感器在健康状态下是可用的，它不需要移动附件健康状态（见健康连续和离散之间的连接。步态OMS和可用设备如图所示。5)。在由于一个髋关节或膝关节执行器锁定关节失效而导致的退化模式下，机器人的行走任务要求移动的附件被替换。处于健康状态。否则，在退化模式下的步行运动是不可能的，任务必须中止。此相互依赖关系存储在称为操作模式管理的数据库中。图表。操作模式按优先顺序排列，最佳选择由自动机选择[22]。

如果设备发生故障，则通过从一个OM切换到另一个OM来进行重新配置，该<, font face="Times New Roman">OM不使用故障设备，可以在降级的设备中执行所需的任务。但是令人满意的方式。

假定机器人正以连续的步态行走，该步态需要健康状态的所有腿部关节致动器，但不需要使用姿势控制器(移动)。突然其中一条腿的膝盖执行器失灵。在这种情况下，机器人将切换到退化离散/不连续门2 OM，并借助姿态控制器。执行机构以适应故障。

图6显示了切换不同操作模式的完整流程图。每个传感器和执行器的健康状态在整个任务期间被监控。取决于运动的类型和设备可用性(处于健康状态)，选择一个操作模式，并相应地向执行任务的执行器发出命令(一系列与步态cy相对应的命令)。)。然后，以测量的形式在每个采样时间步骤之后的响应用于检查运动的一致性，即残差的大小。基于剩余偏差离子，执行器和传感器的健康状况被评估[22]。如果身体方向和关节角度传感器是健康的，关节执行器也是健康的，那么步态周期就是Conti。直到机器人到达目标为止。如果在任何时间点，检测到身体方向传感器的故障，那么任务就会中止(停止)。此外，在有缺陷的情况下如果不止一个传感器有故障，那么任务就失败了。当多个关节执行器出现故障时，也会发生同样的情况。因此，对于最多一个联合传感器故障，不同的组合该方法用于估计其它传感器数据(传感器融合)中对故障传感器的读取，从而使任务能够与所估计的测量一起执行。在最多只有一个乔的情况下执行机构故障时，移动附件的健康状况决定着是否要中止任务，还是通过部署健康的移动附件以及剩余的3小时来继续运动。狂热的双腿。例如，当传感器在任何腿的1或2节点发生故障时，在该腿尖处使用冗余传感器以及来自其他可用传感器的数据(传感器融合)。估计下一节中讨论的缺失的联合位置数据。

3.2.传感器故障调节

传感器故障调节需要冗余的传感器硬件。在所研究的系统中，采用陀螺的MEMS加速度计测量物体的方位和位移。在本作品中，InvenSenseMPU-6000TM系列传感器[23]的成本低于100美元。它将一个三轴陀螺仪和一个三轴加速度计组合在同一个硅模上，并使用三轴复合处理器。传感器融合算法中的SS数据。在本研究中，利用MPU-6000TM传感器的内陀螺仪和罗盘直接测量物体的方位。此外，一个前永恒的愿景系统TEM可以跟踪身体传播，并通过无线通信(例如，通过蓝牙启用的设备)传输数据。腿尖的运动是从安装在底部的照相机上跟踪的。身体的一侧。在星载微处理器中实现了外部和内部传感器数据融合。请注意，这些传感器已经成为每个机器人设备的组成部分。甚至商业上现有的三维运动捕捉系统也可以用来测量雷的位置和腿尖的速度。例如，pti视觉眼球运动跟踪器[24]是高度精确和无校准跟踪的。系统。在这个系统中，在腿尖上附加有不同形状和大小的标记。每个标记都有唯一的ID。建立在碳复合材料结构上的跟踪器捕捉到腿尖上的标记的三维位置。然后将采集到的运动数据输出到计算机上的其他软件中。

作为传感器故障调节的一个例子，考虑了致动器的编码器中的故障。

编码器在电机单元中用作位置传感器。

它被认为是系统EV的鲁棒部分虽然这部分有失败的可能。这种传感器失效的典型原因是过热、接触松、连接器中的水分、安装不良导致的球轴承磨损。这样可以利用传感器冗余来弥补这个错误。假设腿1位置传感器的关节2完全失效，现在无法响应，y和z方向的腿尖位置，接头1的当前位置，和身体俯仰倾角可用于确定接头2的位置。第一条腿在Y和Z方向上的腿尖位置可给出如下所示：

其中l1和l2分别是连接1和2的长度，θ1和θ2分别是关节1和2的关节旋转，ψ是俯仰角，r1y是从体质量中心到的距离。第一条腿的关节1。情商。(14)和(15)可用于查找θ2，如下所示：

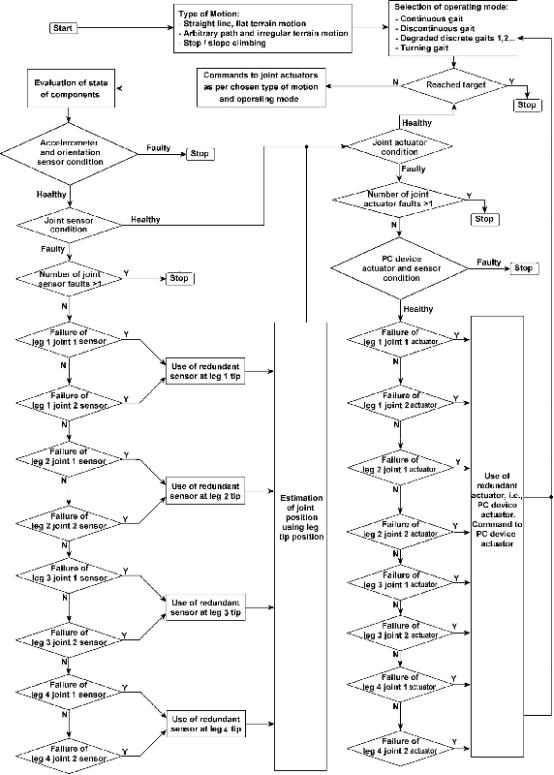
图6.任务和OMS的选择考虑最多一个联合传感器和一个关节执行器故障

图7附加运动子模型的四足动物的词键图及进一步扩展形式的腿

因此，即使传感器故障，也可以估计出近似的联合位置。对于所有其他腿的其他关节传感器故障，也得到了类似的表达式。如属腿部关节感应器诱饵，身体传播控制器（步态模式控制器）使用估计的关节位置代替实际测量。

有一个以if-the的形式实现的控制律库决策支持系统根据系统监控模块中故障诊断工具的诊断结果，执行相应的控制律。

3.3执行器故障调节

第二节中讨论的移动附件装置用于容纳执行器故障(锁定连接故障)。在这种情况下，设备只有在发生执行器故障时才被激活。如果其中一个腿的关节被锁定，那么在腿的其他工作关节的帮助下，腿仍然可以以受限的方式移动。在快步步态的第一阶段，对角线相反的腿移动穹隆。在第二阶段，相同的腿尖接触地面和身体传播发生。在接缝失效的情况下，没有保证在地面上有适当的腿尖接触。萎缩和运动受到严重影响。在所提出的控制策略中，控制两个附属物的位置，使cg身体向失败腿的髋关节移动。实际上，残疾人机器人c一瘸一拐地向前走。

注意，在腿向前运动和身体传播过程中，实际的附属物位置取决于关节被锁定的状态，并且是几何计算的。以上所讨论的控制只有在检测到某一特定腿的关节故障后，L方案才被激活。有一套银行控制法以“如果-然后-否则”块的形式来执行，以解决所有的各种联合故障。决策支持系统根据系统监控模块中的故障诊断工具的结果，执行相应的控制律。在这篇文章中，它已经被考虑到了。红色表示四足动物的健康状况最初是健康的，已知的一个锁定关节故障发生在已知的实例中，控制律被重新配置为预先选择的算法。

4.四足机器人的动力学模型

四足机器人的示意图如图所示。四足机器人的每条腿都有两个自由度，每条腿有两个旋转关节。机器人身体被认为是刚体。图7显示了描述不同子模型之间的互连的机器人的键图。移动附属装置的子模型包含S更低层次的子模型，它们以扩展的形式显示。同样，机器人的一条腿(腿1)的子模型中的较低层子模型以扩展的形式显示。这样的将复杂模型组合成几个较高层次的子模型，再将较高层次的子模型进一步分解为较低层次的子模型等，称为层次对象定向。泰德建模框架平移和角的六自由度机器人机构动力学与欧拉结结构[ 13 ]–17,25,26建模。角速度和平移速度传播与传播利用离子建立了上链键图模型。这就是键合图建模的有效性变得明显的地方。而键合图模型是用运动学方法构造的。由于键合图结(约束)结构固有的功率守恒性质，仅考虑力和力矩平衡方程就能自动满足。导出方程(通过在各种可用的商业软件中实现的算法过程)自动确保模型开发过程中的运动学、动态和能量一致性。除了保持与物理模型结构的紧密相似之外。

在所建立的模型中，每个腿的下节被认为是柔顺的。因此，它被看作是一个棱柱状的链接。棱柱连杆的详细建模在[17，25，27]中讨论。波在符号软件[14，28，29]中建立了含有棱柱连杆的四足体动力学模型和运动附属物装置的ND图模型。

图的上部。7给出了带移动附件装置的四足机器人的词键图。注意，相应的标量键图形式(它与交织键非常复杂，并且是不适合于在这里表示)被输入到软件的模块化形式(使用子模型和层次分解)的模型开发和仿真。读者可参考作者“前30–[ 32 ]对四足机器人建模的细节和计划调度的运动模式下的各种步态。

5.。实验装置

为了进行实验验证，开发了移动附件装置。两组齿条齿轮装置安装在四足机器人上，如图8所示。12 V直流减速电机（有刷直流电机100:1POLOU制造的金属变速箱)用于操作齿轮。配合架是用铝制成的。小齿轮的旋转运动在平台内产生齿条的再运动。提供的指南。两台直流电机均通过20A双直流电机驱动，由ArdiunoMegaADK控制器控制。齿条-小齿轮装置的主电源为12V-10安培.采用三轴加速度计测量人体的方位.。用Ardiuno编写的程序读取传感器数据，并相应地向两个电机发出功率信号。

研制的机器人长0.5米，宽0.42米，距地面标称高度0.48米。除了腿、身体、执行机构和控制器外，它的重量约为15公斤。机器人是为马西而设计的。妈妈15公斤有效载荷，不包括它的自重。这个有效载荷的一部分将被安装在移动的附件上，这样机器人的重心就可以被少量移动以转移BOD。任何腿的重量。马达是根据这个载荷来调整大小的。在他们的实验室里，作者们已经没有几台马克逊齿轮直流电机，可以提供比设计的连接更多的功能。t扭矩。这些马达虽然尺寸过大，但为了节省成本，已在机器人腿的髋关节和膝关节中使用。在实验设置中，有效载荷目前没有安装，因此从外部可以看到闪避器和控制器。

通过优化腿部形状和驱动系统，可以降低机器人的自重.。用螺旋螺母机构代替电动膝关节，人形腿传动[1]，电缆交流。模拟肌肉的动作，可以用来减轻体重，形成紧凑的设计。此外，由于没有有效载荷，移动附属物需要大量运动才能通过。失足腿的体重。当部分有效载荷将支持在移动附件上时，机器人车身CG可以通过移动附件的小运动而被移动。因此，BODY宽度可减小到0.2米左右。然而，身体长度不能进一步减少，因为这将减少腿的步长和运动速度。杂交(轮式腿)卡西诺六足动物II与滚轮[1]和更新卡西诺六足III与全方位车轮使用商用热塑性合金作为车身结构材料和锂-宝电池作为车载电源。这么轻的伴侣目前的机器人还可以探索RIE和动力源，以减轻重量。此外，移动平台中的齿条和小齿轮布置也是初步设计。二维(2D)移动机器人离子/XY/定位台可采用滚珠丝杠机构或更好的钢骨齿带传动系统重新设计。这种重量轻、速度快的定位台是通勤的。可以从Macron DynamicsiselAutomation(前身为Techno Inc.)、智能驱动程序、Dover Motion(Invetech部门)和其他各种来源获得。本文主要研究的是在四足机器人中作为概念的证明，因此，机器人的优化设计超出了其核心目的。

在研制的机器人中，通过上位机或处理器来选择操作方式。每个腿的联合旋转是计算所需的操作模式。代码是在open-pcs u中生成的。唱函数块。命令通过主控制器和控制器区域网络(CAN总线)发送给从控制器。执行器和传感器的健康状况被持续监测和重新配置。如果可能，将执行配给。这个控制循环一直持续到机器人到达目标。控制周期的主要活动如图6所示。

6.成果和讨论

通过在键合图模型上的仿真，验证了前面部分讨论的故障调节策略。这些参数和它们的数值列于表1。n表1。关节致动器控制器增益已被手动调整，以快速和几乎过阻尼的响应和稳态误差消除，同时确保。

图8.实验装置：带有移动附件装置的四足机器人

良好的相对稳定性。通过对所开发的模型进行模拟，并在实验中使用这些调谐值进行了启发式调谐。调优的基本值是摘自Maxon电机文档中给出的应用实例。通过仿真对运动附属物控制器的增益值进行了调整，并采用了相应的实验方法。附注t运动附件的增益值似乎很小，因为导轨是光滑的(允许线性运动且施加的力很小)，车身的俯仰和滚动很小(重量分量在X方向和Y方向小)，有效载荷小，有效电机特性常数(如果有的话)，包括齿轮比(如果有的话)很小。注意，当有效载荷的一部分安装在移动附件、移动附件电机必须调整大小，控制器增益必须相应地增加。这将在下一个版本的开发过程中处理。在这些四足动物中，有许多其他的附加功能，如有效载荷、更高的速度、更好的行走和运行稳定性、以及多重容错等。

6.1传感器故障调节

假设四足动物的健康状况最初是健康的，传感器工作得很好，突然间，一个关节传感器在第一腿的第二个关节发生故障，而四足动物以小跑的步态移动。

如图所示。9(A)传感器在30.3秒时发生故障，由故障检测和隔离模块及时检测该故障。然后，通过传感器冗余作为磁盘，得到传感器值。在3.2节中使用。无花果。9(B)显示高达30.3秒的真实传感器读数(即，与图相同)。9(A)及其后估计的传感器读数。从图中看。9(B)有一些偏差NS在估算测量中由于建模误差、测量中存在噪声以及四足类动物与地面的柔性接触。在这里，机器人以小跑的步态移动。无花果。10(A)显示联合1 r所有腿的轮转还有无花果。10(B)显示所有腿的关节2旋转，但不包括已在图1中显示的第1腿的转动。9(B)。注意，腿1和2的平均关节旋转是相似的，平均连接。腿3和4的t旋转是相似的。这是由于机器人的后向腿配置(或立场)，如图所示1.在快步步态中，四足动物在正Y方向上移动，如图1所示。11(a)，而其Z向移动示于图1中。11(b)。结果在图1中。11示出了移动性能不是HIN,通过使用估计的测量结果。

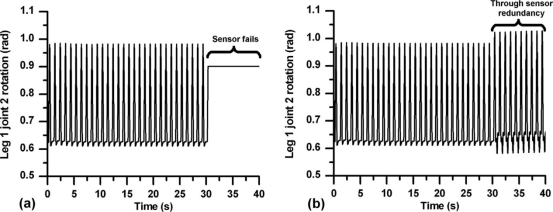图9.LEG 1连接2传感器输出(A)原始信号和(B)高达30.3 s的原始信号，并随后通过传感器冗余输出。

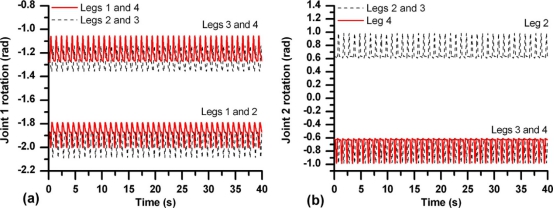
图10.关节旋转：(A)关节1和(B)关节2

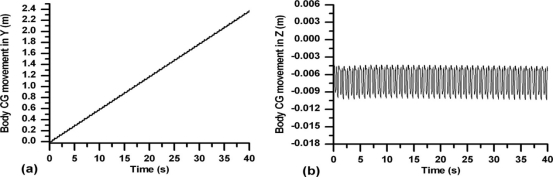
图11.体CG向(A)Y和(B)Z方向运动。

6.2.致动器故障调节

在2.4s时，模拟了第1腿关节2的突然失效。根据控制策略，在第一腿向前运动时，附属物装置保持在中心附近，而在下一阶段，则试图使其保持在中心附近。在最外面的一侧，使由此产生的体重在身体繁殖过程中作用于腿1的髋关节。无花果。12例显示体CG向Y方向运动。因为附件的重量年龄，控制器确保腿1尖端与地面的适当接触和有效的身体传播。如果四足机器人在接下来的四个步态周期中继续运动，而不需要Th的贡献。移动附属物的距离为0.362米，因为有时地面接触力在第一腿的尖端消失，而在其他时候则变得很小，从而降低了牵引力。论奥特她的手，机器人移动0.430米与控制运动的附属物。如果只考虑故障后的距离，那么它是0.262米没有移动附属物和0。330有移动的附属物，即约26%的额外距离是通过故障调节。因此，由于t的控制策略，它的运动性能得到了全面的提高。移动附件装置。图13显示了x和y方向的齿条运动。PC机设备一直处于中心位置，直到出现任何关节执行器故障。此后，x和Y方向以协调的方式执行，以将体重转移到腿1。如图所示。13.机架运动模式受步态模式控制，pc装置是POSI。仅在第一条腿向前运动时处于中心位置。对于其他三条腿的向前运动，机架要适当地远离中心位置。机架运动APPEAr为6.2.。致动器故障调节

在2.4s时，模拟了第1腿关节2的突然失效。根据控制策略，在第一腿向前运动时，附属物装置保持在中心附近，而在下一阶段，则试图使其保持在中心附近。在最外面的一侧，使由此产生的体重在身体繁殖过程中作用于腿1的髋关节。无花果。12例显示体CG向Y方向运动。因为附件的重量年龄，控制器确保腿1尖端与地面的适当接触和有效的身体传播。如果四足机器人在接下来的四个步态周期中继续运动，而不需要Th的贡献。移动附属物的距离为0.362米，因为有时地面接触力在第一腿的尖端消失，而在其他时候则变得很小，从而降低了牵引力。论奥特她的手，机器人移动0.430米与控制运动的附属物。如果只考虑故障后的距离，那么它是0.262米没有移动附属物和0。330有移动的附属物，即约26%的额外距离是通过故障调节。因此，由于t的控制策略，它的运动性能得到了全面的提高。移动附件装置。图13显示了x和y方向的齿条运动。PC机设备一直处于中心位置，直到出现任何关节执行器故障。此后，x和Y方向以协调的方式执行，以将体重转移到腿1。如图所示。13.机架运动模式受步态模式控制，pc装置是POSI。仅在第一条腿向前运动时处于中心位置。对于其他三条腿的向前运动，机架要适当地远离中心位置。

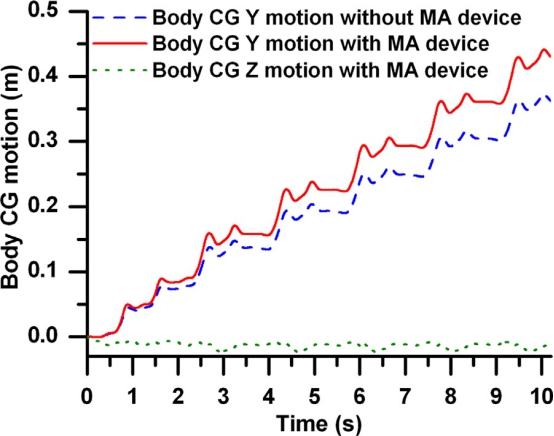
图12.身体CG运动

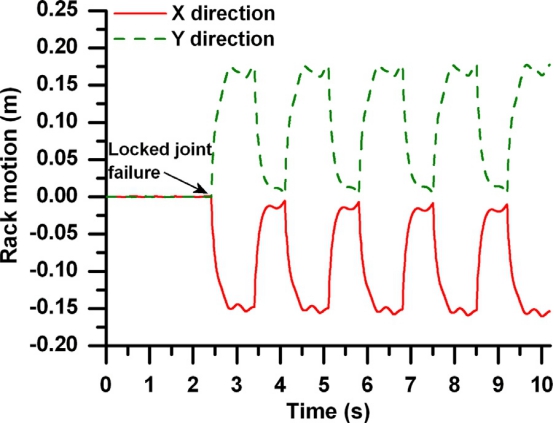
图13.机架运动

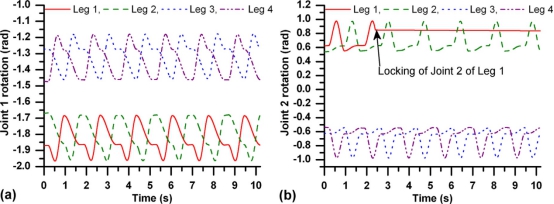
图14.腿关节旋转：(A)关节1，(B)关节2

图14(A)和(B)显示同一时期内所有腿的关节分别为1和2旋转。这些关节旋转受步态的控制，即使在上锁的joi之后也不会改变。其中一个腿关节骨折。

上述仿真结果也通过实验得到了验证。这里也考虑了腿1的连接2的失效。这是通过固定核心计数器变量进行的实验模拟。值在maxon电机控制器中的值。

图15.在实验中使用齿条齿轮装置进行闭锁连接故障的断齿(A)靠近中心的MA，(B)MA远离中心。

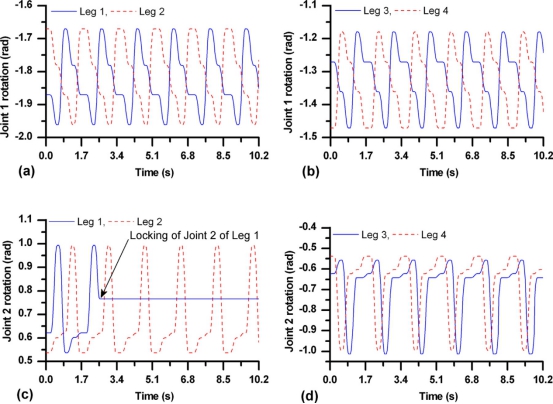
图16.小腿步态实验中的关节旋转：(A)关节1腿旋转1和2(B)关节1腿3和4转动，(C)关节2腿1和2旋转，(D)关节2轮三四条腿。

一定的时间，继续提供期望的关节扭矩，以防止其旋转。无花果。15张照片显示，在重新配置机架齿轮d的锁定接头失效的实验中，很少有截图。逃避。机器人测量数据存储在便携式计算机中。因此，从机器人到计算机的USB电缆可以在照片中看到。同样，机器人的电源也是提供的。从交流电源到直流电源包外部，并且有从电源包到每个执行器的独立的电源电缆。如果电源是从车载电池中提取的，那么baTREY本身成为一个有效载荷，为了将SUffi的重量转移到失败的腿上，它必须安装在机架上。这会阻碍机架运动的视野。当前的机器人是n正在开发中的实验原型，它将经历其他几个特性的补充。请注意，在机器人的最终开发版本中，将有车载电源和数据。一个记录器，这将消除使用外部电缆。

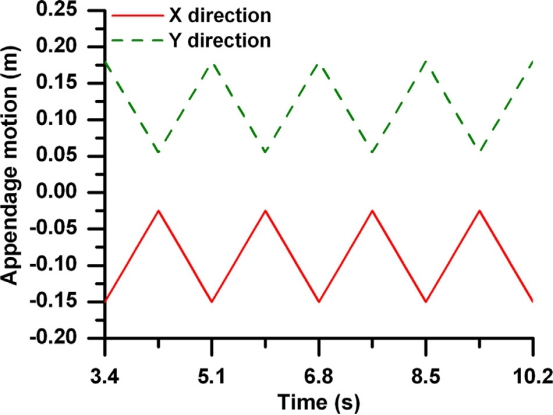
图17.在机器人故障状态下，在实验过程中进行了短时间的附属物运动。

图16(A)和(B)分别显示关节1腿1-2和3-4旋转，而图1。16(C)和(D)在实验中分别显示了腿1-2和3-4的关节2次轮转。机架运动故障期间的状态如图所示。17.。据观察，如果没有这种移动的附属物装置，腿部失灵的四足动物在5个周期内的距离为0.30米左右，而附肢为d。它的飞行距离约为0.348米。如果只考虑故障发生后的行程，那么它是0.222米没有移动附件，0.27与移动附件，即约22%的额外距离通过故障调节覆盖。在实验中与通过模拟得到的距离的差异可以归因于模型的不确定性，如Fri。在地面与腿尖之间产生接触面的可变滑移，在执行机构中产生间隙，在试验过程中拖在地面上的电缆，估计不准确。丁模型参数(主要是惯性矩)，电机性能与响应延迟不匹配，以及其它未建模的外部扰动。

7. 总结

执行器故障干扰四足机器人的运动。本文介绍了安装在四足机器人上的两套可控制的移动附件装置，包括齿条和小齿轮布置。四足机器人的执行器故障(锁合故障)调节。通过重构控制，发现它们在故障调节方面具有相当的ffi。因为被控制的m在腿部向前运动时，可适当地将体重转移到失败的腿上，确保失败的腿部与地面良好接触，提供牵引。RCE在其支持阶段。仿真研究和实验表明，由于运动附件装置的作用，该机器人比WITH机器人能更远地运动。干掉它。同样数量的闸门周期覆盖的距离改善略大于20%。因此，由于控制策略的实施，它的运动性能得到了全面的提高。带有移动附件装置的ED。另外，一个传感器故障等空间战略的提出。可以看出，在腿关节（髋关节或膝关节）传感器故障后，可以进行进一步的运动O。UT通过传感器融合算法，利用来自其他传感器的数据。传感器故障和执行器故障的调节是相互排斥的(见图)。6)因此，开发的机器人可以模拟从一个传感器和一个执行器故障中立即恢复。冗余硬件在执行机构(这里，移动附件)和传感器(这里，腿尖位置传感器)增加了重量和co。而他们提高了机器人的整体可靠性和性能。本文介绍了冗余硬件(移动AP)中的人体定位传感器和执行器及传感器的故障。)还没有考虑过。所描述的机器人还处于发展阶段，在从其他故障中恢复方面还处于发展阶段，包括冗余硬件和其他故障的恢复。传感器、多传感器和执行器故障、运动稳定性和提高速度都在考虑之中。

致谢

M. M.Gor、P.M.Pathak和A.K.Samantaray的工作由印度DST资助，由印度-韩国科学技术联合研究机构批准。INT/韩国/P-13。杨洁敏与S的工作。W.Kwak由大韩民国国家研究基金会资助，VIDE基金编号。NRF-2011-0027705。

参考文献

[1]F. Tedeschi, D. Cafolla, G. Carbone, Design and operation of cassino hexapod II, Int. J. Mech. Control 15 (1) (2014) 19–25.

[2]F. Tedeschi, G. Carbone, Design of hexapod walking robots: background and challenges, in: M.K. Habib (Ed.), Handbook of Research on Advancements in Robotics and Mechatronics, IGI Global, USA, 2015, pp. 527–586.

[3]H. Berriri, M.W. Naourar, I. Slama-Belkhodja, Easy and fast sensor fault detection and isolation algorithm for electrical drives, IEEE Trans. Power Electron. 27 (2) (2012) 490–499.

[4]I. Jlassi, S. Khojet, E. Khil, A MRAS–Luenberger observer based fault tolerant control of pmsm drive, J. Electr. Syst. 10 (1) (2014) 48–62.

[5]B. Ould Bouamama, K. Medjaher, M. Bayart, A.K. Samantray, B. Conrard, Fault detection and isolation of smart actuators using bond graphs and external models, Control Eng. Pract. 13 (2) (2005) 159–175.

[6]A.K. Samantaray, K. Medjaher, B. Ould Bouamama, M. Staroswiecki, G. Dauphin-Tauguy, Diagnostic bond graphs for online fault detection and isolation, Simul. Model. Theory 14 (3) (2006) 237–262.

[7]Y.-J. Lee, S. Hirose, Three-legged walking for fault tolerant locomotion of a quadruped robot with demining mission, in: Proc. IEEE/RSJ Intl. Conf. intelligent Robots and Syst., 2000, pp. 973–978.

[8]J.-M. Yang, Fault-tolerant gaits of quadruped robots for locked joint failures, IEEE Trans. Syst. Man Cybern.-Part C 32 (4) (2002) 507–516.

[9]J.-M. Yang, Crab walking of quadruped robots with a locked joint failure, Adv. Robot. 17 (9) (2003) 863–878.

[10]J.-M. Yang, Two-phase discontinuous gaits for quadruped walking machines with a failed leg, Robot. Autonom. Syst. 56 (9) (2008) 728–737.

[11]M. Blanke, M. Kinnaert, J. Lunze, M. Staroswiecki, Diagnosis and Fault-Tolerant Control, Springer, London, 2006.

[12]R. Isermann, Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance, Springer, London, 2005.

[13]D.C. Karnopp, D.L. Margolis, R.C. Rosenberg, System Dynamics: Modeling and Simulation of Mechatronic Systems, Fourth edition, John Wiley Sons, New Jersey, 2006.

[14]A. Mukherjee, R. Karmakar, A.K. Samantaray, Bond Graph in Modeling, Simulation and Fault Identification, CRC Press, FL, 2006.

[15]W. Borutzky, Bond Graph Methodology Development and Analysis of Multidisciplinary Dynamic System Models, Springer, 2010.

[16]G. Dauphin-Tanguy, Les Bond Graphs, Hermes Science, Paris, 2000.

[17]R. Merzouki, A.K. Samantaray, P.M. Pathak, B. Ould Bouamama, Intelligent Mechatronic Systems, Springer-Verlag, London, 2013.

[18]M. Karthikeyan, A. Bisoi, A.K. Samantaray, R. Bhattacharyya, Sommerfeld effect characterization in rotors with non-ideal drive from ideal drive response and power balance, Mech. Mach. Theory 91 (2015) 269–288.

[19]S. Junco, A. Donaire, A. Achir, C. Sueur, G. Dauphin-Tanguy, Non-linear control of a series direct current motor via flatness and decomposition in the bond graph domain, Proc. IMechE. Part I: J. Syst. Control Eng. 219 (2005) 215–230.

[20]M.M. Gor, P.M. Pathak, A.K. Samantaray, J.-M. Yang, S.W. Kwak, Reduction in body disturbance of quadruped robot using two moving appendage, in: Proc. Intl. Conf. Bond Graph Modeling and Simulation (ICBGM’2014), 46, Monterey, California, July 6-10, 2014, pp. 85–92.

[21]V.L. Krishnan, P.M. Pathak, S.C. Jain, A.K. Samantaray, Reconfiguration of four-legged walking robot for actuator faults, in: Proc. IMechE Part I: J. Systems and Control Engineering, 225, 2011, pp. 1–16.

[22]A.K. Samantaray, B. Ould Bouamama, Model-based Process Supervision, Springer-Verlag, London, 2008.

[23]C. Llamas, M.A. González, C. Hernández, J. Vegas, Open source platform for collaborative construction of wearable sensor datasets for human motion analysis and an application for gait analysis, J. Biomed. Inf. 63 (2016) 249–258.

[24]J. Huang, W. Xu, S. Mohammed, Z. Shu, Posture estimation and human support using wearable sensors and walking-aid robot, Robot. Autonom. Syst. 73 (2015) 24–43.

[25]T.K. Bera, R. Merzouki, B.O. Bouamama, A.K. Samantaray, Force control in a parallel manipulator through virtual foundations, Proc. IMechE Part I: J. Syst. Control Eng. 226 (8) (2012) 1088–1106.

[26]J.J. Craig, Introduction to Robotics Mechanics and Control, 3rd ed., Pearson Education, USA, 2005.

[27]T.K. Bera, A.K. Samantaray, R. Karmakar, Bond graph modeling of planar prismatic joints, Mech. Mach. Theory 49 (1) (2012) 2–20.

[28]A.K. Samantaray, A. Mukherjee, User Manual of Symbols Shakti, Indian Institute of Technology Kharagpur, High Tech Consultants, 2000.

[29]A. Mukherjee, A.K. Samantaray, System modelling through bond graph objects on symbols 2000, in: Simulation Series, Society for Modeling & Simu-lation International (SCS), 33, 2001, pp. 164–170.

[30]M.M. Gor, P.M. Pathak, A.K. Samantaray, J.-M. Yang, S.W. Kwak, Dynamic modeling and simulation of compliant legged quadruped robot, in: Proc. INaCoMM 2013, Roorkee, India, 2013, pp. 7–16.

[31]M.M. Gor, P.M. Pathak, A.K. Samantaray, J.-M. Yang, S.W. Kwak, Control oriented model-based simulation and experimental studies on a compliant legged quadruped robot, Robot. Autonom. Syst. 72 (2015) 217–234.

[32]M.M. Gor, P.M. Pathak, A.K. Samantaray, J.-M. Yang, S.W. Kwak, Control of compliant legged quadruped robot in workspace, Simulation 91 (2) (2015) 103–125.

柔性四足机器人通过移动附件机构的故障调节

作者：MM Gor ， PM Pathak ， AK Samantaray ， JM Yang ， SW Kwak

来源： 《Mechanism & Machine Theory》 , 2018 , 121 (1) :228–244

摘  要

与其他腿部机器人相比，四足机器人提供了更好的稳定性和速度。然而，其关节执行器或传感器故障严重影响了运动。交流导航仪和传感器的策略本文提出了柔顺腿四足动物的错误调节。提出了一种正交安装的移动附件机构，以解决锁紧关节失效问题。这些附属肢肢ES作为机架安装的惯性，在执行器失效时执行受控运动。提出了一种传感器故障调节策略。四足R的三维多体动力学模型利用键合图建模方法，提出了OBOT及其故障调节策略。通过仿真和实验验证了该控制系统的性能。

1. 介绍

移动机器人大多遵循三种设计方案。第一种机器人是由轮子支撑的，它允许在平坦的地形上高速运动，但是在不均匀的表面上操作这样的机器人是的习俗。完成攀爬等具体任务。第二种是以人形腿为基础，以速度为代价，在地形起伏、避障等方面提供更好的运动能力。T型海鸟是一种混合设计，结合车轮在腿尖，以提供一个折衷的设计。卡西诺六足机器人^[1]是一种混合移动机器人，可以在平坦的地面上滚动行走。在不规则的地形上。对于多腿机器人，需要三条合适的腿来保持静态稳定性.。因为至少有一条腿需要从地形上抬起运动时，所需的最小腿数是四条。随着腿数的增加，机器人在移动过程中的稳定性增加，机器人可以在出现故障的情况下继续工作。几条腿^[1]。此外，多余的腿也可以作为手部署，以便进行操作。这推动了六足类机器人^[2]和腿部数量更多的机器人的发展。然而，六足机器人的运动速度和灵活性都低于四足机器人。对于典型的任务，如避障、爬台阶等，腿越多意味着越复杂。它的模式。人们可以想象出一种想象中的马匹大小的六条腿动物，试图清理马术圈，以理解与太多四肢相关的问题。腿的运动不应该在彼此少，因此越来越多的腿，步长减少机器人的长度的增加（如蚂蚁、蜈蚣、千足虫）。在这方面，四条腿的机器人它在运动稳定性与运动灵活性和速度之间提供了很好的折衷。然而，与六足类动物不同的是，六足类动物最多可以承受两条腿的失效(不包括某些特殊情况)，四足动物在腿故障时不能很好地操作。本文正是针对四足动物腿部的这种故障，提出了部署冗余哈尔的建议。以移动附属物的形式来克服这个障碍。

安全性和可靠性是任何汽车系统设计中的关键问题。四足机器人是指在危险的环境中工作。传感器和执行器故障更有可能发生在在这样的环境下，机器人被投入工作.。因此，容错控制(FTC)和重构是四足机器人的一个新兴研究领域。在文献中，人们找不到传感器福尔。不能容纳四足机器人。然而，很少有研究人员致力于传感器故障检测和隔离电气系统^[3，4]和气动系统^[5，6]。位置传感器故障通过分析冗余、硬件冗余或两者同时检测和分离。硬件冗余是一种可靠的解决方案，但由于成本和空间的限制，其使用受到限制。分析基于冗余的解决方案需要一个完善的、有效的数学模型，用于生成残差，即预测的无故障测量和实际测量之间的差异。传感器读数^[5]。这些残差可以用来检测和隔离机器人系统中的各种故障。

在执行器的情况下，锁定关节失效是一种运动故障，在这种故障下，关节不能移动，并被锁定在适当的位置。然而，身体的支持能力被保留。由于这个特性，f如果适当地部署，固定的腿可能对机器人的运动有部分贡献。由于轴承摩擦、滑脱等原因，锁紧接头失效更为常见。离合器的平，齿轮的断齿堵塞电机，转子轴的不对中/弯曲。在这种情况下，可以通过实现容错步态模式来实现运动。或者将控制规则应用于冗余硬件。^[7-10]中提出了不同的容错步态，以解决锁定的关节故障。通过重新配置^[11，12]调整故障是accom由于备用备用设备(称为硬件冗余)的实时部署/激活，取代了故障执行器，并使控制律适应于修改后的系统结构。

提出了传感器和执行器故障调节策略。在故障状态下，传感器/执行器可能会有不同的反应。在这里，人们认为这些在福尔岛根本没有反应。泰州。冗余传感器用于检测传感器故障.。执行器故障被认为是锁紧型故障。为了适应这一故障，实现了两个移动附件(MA)。提出了齿条式小齿轮的布置形式。附件装置作为一个冗余硬件，只有当基本四足机器人遭遇关节锁定故障时才能激活。本文的工作表明，通过这种布置，可以有效地实现故障(锁合故障)调节。为了演示所提出的控制策略。采用键合图方法^[13-16]建立了步行机器人的MIC模型。键合图是一种从物理范式本身出发进行系统建模的effi工具，各种控制策略都可以实现。通过修改物理范式发展^[17-19]。

本文的结构如下。第二节介绍了所提出的移动附件装置。第三节介绍了传感器和执行器故障(锁定接头)的补救措施。动态仿真模型第4节和第5节分别介绍了实验中使用的物理模型。在第六节中，给出了验证所提出的策略的结果。最后，第六节对本文进行了总结。

2.移动附属物装置

图中给出了一个具有两个移动附件的柔顺腿四足机器人的原理图。1.。四足机器人的每一腿由两个环节组成。链接1与机器人体t相连。旋转关节(髋关节)，而链接2是通过旋转关节(膝关节)与链接1组装。对于四足机器人的建模，把框架{A}看作惯性系，车身固定框架{B}连接在机器人身体的重心上。在每个腿上，框架{0}固定在髋关节，{1}固定在关节1。在这里，帧{0}和{1}重合在一起河。另外，框架{2}固定在关节2或膝关节和框架{3}固定在腿的顶端。

移动附属物装置安装在车身顶部。该装置也称为姿态控制(PC)装置，因为它用于控制四足机器人的姿态[20]。然而，控制str姿态控制策略不同于故障调节策略。本文首先介绍了pc装置在平面矢状面重构中的应用。四足机器人模型。本文试图通过三维模型的重构来适应锁定节点的失效，并通过实验验证了该方法的有效性。

移动附件由齿条和小齿轮组成，其中小齿轮由电机操作。机架只能沿所提供的路径/导轨执行直线运动。机架运动重心位置的变化(CG)。因此，通过控制小齿轮的旋转运动，可以控制物体的方向。X和Y的体位，即ψaNdθ可以通过两个移动附件装置来控制。

为了概念化，在图1中示出仅控制俯仰角(ψ)的移动附件的示意图。

具有中心质量的可线性移动的齿条起到运动附件的作用。

控制方向ψ的移动附件，沿y方向有齿条运动。给出了动附属物在Rack 1上相对于惯性系{A}的CG的位置。

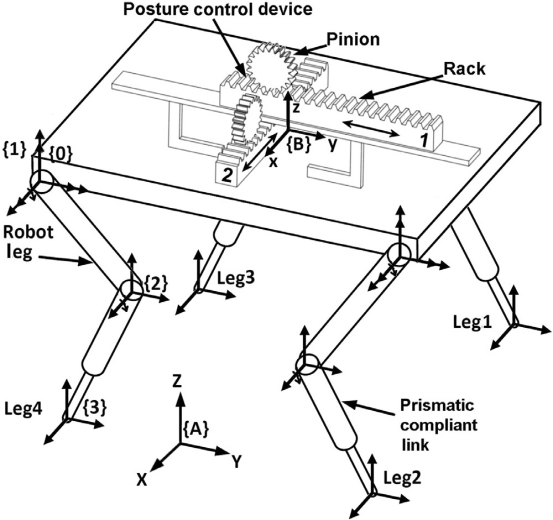
图1 四足机器人移动附属物机构原理图。

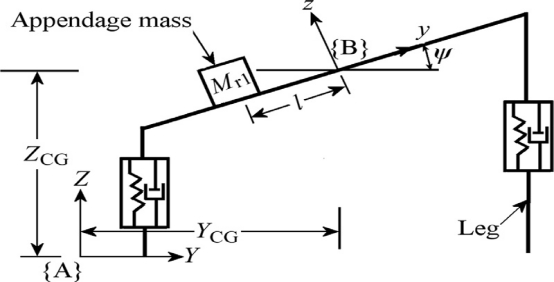
图2 控制俯仰角的移动附件的示意图。

其中l是从移动附属物质量中心到身体中心的距离，是小齿轮节圆半径(P1)和小齿轮(θp1)相对于体框架、YCG和ZCG是体CG相对于帧{A}的坐标。给出了齿条在Y方向和Z方向上的速度：

物体在物体顶部的位置决定了俯仰角。因此，对于期望的物体位移(俯仰角)，控制律可以写成：

其中MR1是机架1的质量，g是重力加速度，ψd和ψ分别是物体在X轴附

近相对于惯性Re的理想和实际的角度位移。F_1帧{A}、KP1∗、KV_1∗和Ki_1∗分别是控制器的比例增益、导数增益和积分增益。假设具有小特性常数km的快速动作电机，armature电阻RM，和电感，在低转速的电机转矩可近似等于失速转矩，即T1 =公里（V1−公里θ˙P1）/ RM≈kmv1 / RM。这种假设尤其重要。由于采用高减速齿轮时，有效电机特性常数显著降低，因此适用于齿轮传动的UE。作为一个简单的证明，利用键合图的性质，g的一个组合代表电机(模数k)的yrator和代表齿轮(模数r1)的变压器产生具有旋转模或电机特性常数k/rk的回转器或等效马达。自此齿条齿轮电机遇到的扭矩与齿条的位置成正比，即齿条的角度位置。  

  全套毕业设计论文现成成品资料请咨询微信号：biyezuopin QQ：2922748026     返回首页 如转载请注明来源于www.biyezuopin.vip