|
ground: rgb(255, 255, 255); color: rgb(34, 34, 34); font-family: 宋体; font-size: 12pt;">越来越多的专家学者开始分析正常人与患者之间生物电信号方面的差别,如肌电信号、脑电信号等方面。肌电信号包含了反映运动模式和运动意愿的丰富信息[17]。基于对肌电信号的分析,可以直接对外周神经细胞、肌纤维、神经肌肉接头等处的功能情况进行评估。Ei-Abd等人[18]在研究脑损伤患者和正常人肘关节屈伸运动时的肌电信号变化中发现,58%的脑损伤患者的上肢有主动肌和拮抗肌同时收缩;当肘关节快速运动时,正常人有3相肌电活动,而脑损伤患者中66%呈主动肌持续性电活动。季林红等人[19]采用基于自适应Chirplet 分解的时频分析方法,对15例偏瘫患者在完成快速伸肘过程中肱二头肌的肌电信号进行分析,利用最优Chirplet 时频参数对脑损伤导致的肌强直症状进行定量评估。研究结果表明基于肌电信号Chirplet时频参数的功能评价与相应的简式Fugl-Meyer功能评价存在较好的线性关系。
Fu[20]等人以7个健康人和11个脑卒中患者为研究对象,就由于脑损伤导致上肢运动功能障碍患者,能否通过想象患肢的动作使EEG的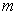 节律出现ERD特征模式进行了对比实验研究。实验结果显示在脑部运动控制功能障碍患者的EEG中仍可以侦测到 节律出现ERD特征模式进行了对比实验研究。实验结果显示在脑部运动控制功能障碍患者的EEG中仍可以侦测到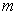 节律的ERD特征模式,不过其ERD的峰值明显比健康人的低;Berardelli 等[21],用电刺激运动皮层后,发现脑卒中患者MEP消失,中枢运动潜伏期延长。Heald等[22]研究发现,中风发作后72小时检测的中枢性运动传导时间(Central motor conduction time,CMCT)与功能预后及死亡率密切相关。国内外众多专家学者对大脑与肌肉之间的信息传递方向进行研究。Ferruccio Panzica[23]等人利用部分直接相干法分析癫痫患者脑电信号与肌电信号的关联程度,研究发现癫痫患者与健康人相比,癫痫患者的信息传递较为紊乱,既有大脑流向肌肉的信息传递,也有较强的信号是从肌电信号传向脑电信号。类似的,Tatsuya Mima[24-25]等人也做过这方面的研究。 节律的ERD特征模式,不过其ERD的峰值明显比健康人的低;Berardelli 等[21],用电刺激运动皮层后,发现脑卒中患者MEP消失,中枢运动潜伏期延长。Heald等[22]研究发现,中风发作后72小时检测的中枢性运动传导时间(Central motor conduction time,CMCT)与功能预后及死亡率密切相关。国内外众多专家学者对大脑与肌肉之间的信息传递方向进行研究。Ferruccio Panzica[23]等人利用部分直接相干法分析癫痫患者脑电信号与肌电信号的关联程度,研究发现癫痫患者与健康人相比,癫痫患者的信息传递较为紊乱,既有大脑流向肌肉的信息传递,也有较强的信号是从肌电信号传向脑电信号。类似的,Tatsuya Mima[24-25]等人也做过这方面的研究。
2 基于脑电分析运动功能障碍的特征提取方法
特征提取是脑电信号处理过程中非常重要的环节,提取类别之间区分度大的特征将会大大降低特征分类的难度。特征提取是指通过一系列的映射和变换,降低原始信号空间的维数,使得一些能反映事物特点的,但不易通过观察或者检测的特征从原始的特征域中显示出来。下面简单介绍几种特征提取的方法:
2.1 时域分析法
时域分析法主要是根据采集到的脑电信号(如电压信号)直接提取波形特征,比较直观。早期的脑电图分析主要采用时域分析方法。通过对脑电时域波形分析,以获取一些重要的脑电时域特征,如方差分析、直方图分析、相关分析、峰值检测和过零点检测等。Abduljalil Mohamed[26]等人将单位时间窗的多种时域特征(包括求和值、均值、标准差、过零点数和能量值)作为特征值组成特征向量,利用DS证据理论对K近邻算法进行改进,对是否患有癫痫疾病进行分类识别,取得了较好的实验结果。
时域分析方法由于提取的特征过于简单,且含有较多的噪声,已经很少被使用。但是由于该方法算法简单,计算量小,对于提高脑电信号的处理效率依然具有参考价值。
2.2 频域分析法
频域分析主要是利用傅立叶变换,将原始的时域信号转换到频域中,提取频域中的特征。频域分析方法主要是EEG的功率谱估计,把幅度随时间变化的脑电波变换为脑电功率随频率变化的谱图,可以直接观察EEG中的β、α、δ、θ等节律的分布与变化情况。常用方法有功率谱估计、AR模型功率谱估计、双谱分析[27]等。这类方法简单,使用较多。但是信息单一,对于非平稳性很强的自发EEG来说,识别精度比较低,但比较是适用于较为简单的BCI系统中两种思维任务的分类。Junhua Li[51]等人利用Lomb-Scargle谱分析法对运动想象的脑电信号进行特征提取,再利用支持向量机(SVM)和Denoising Autoencoder(DEA)法进行模式分类对比分析。Lomb-Scargle谱分析法相比于传统的功率谱估计法,在对分类结果没有造成显著影响的情况下,可以大大缩短EEG信号的长度。
2.3 时频域分析
时频分析方法可以得到时-频谱,我们可以得到在整个时间段内的每一个时刻的频律成份分布情况,也可以得到频率成分随时间的变化情况。这就给我们分析非线性、非平稳的信号提供了有力的工具。目前较常见的时频分析方法有:短时傅立叶变换,小波变换,Wigner-Ville分布[28]等[29]。
2.3.1短时傅立叶变换
短时傅立叶变换是将非平稳信号假设成分段平稳,通过一个固定长度的滑动窗,分段的截取信号,并对所截取的信号进行傅立叶变换。这样就可以得到信号x(t)在任意时刻的频谱。
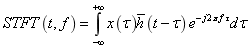 (1) (1)
其中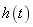 为窗函数, 为窗函数,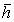 为窗函数的共轭。短时傅立叶变换的模值的平方,称为谱图Spectrogram(SPEC),它表示能量随时间和频率的分布状况。 为窗函数的共轭。短时傅立叶变换的模值的平方,称为谱图Spectrogram(SPEC),它表示能量随时间和频率的分布状况。
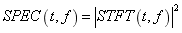 (2) (2)
短时傅立叶变换的主要缺陷是窗口长度求解前需固定,不能随着信号分析需要进行而调节。根据Heisenberg测不准原理,短时傅立叶变换时频表示的时间分辨率和频率分辨率是相互矛盾的不可能在时间和频率两个方向同时获得高的分辨率。
2.3.2小波变换
小波变换克服了短时傅立叶变换窗口长度固定,不能满足不同频率需要不同分辨率的要求的缺点,时间窗长度可随需要不同而改变。小波变换是假设信号中频率高低不同的分量具有不同的时变特性,频率较低成分频谱随时间变化的较慢,频率较高成分频谱随时间变化快。根据上述条件,对时间轴和频率轴进行调整,通过刻度的非均匀划分,达到获得较好时频分辨率的目的。
信号x(t)小波变换的定义式为:
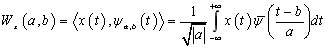 (3) (3)
式中,a为尺度因子,b为平移因子,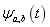 为小波基函数,是小波基 为小波基函数,是小波基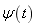 经过平移和伸缩得到的。 经过平移和伸缩得到的。
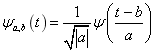 (4) (4)
小波变换的系数幅平方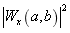 被称为小波谱,它属于仿射类时频表示。将 被称为小波谱,它属于仿射类时频表示。将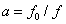 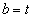 代入可得到小波变换的时频表示: 代入可得到小波变换的时频表示:
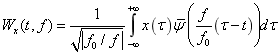 (5) (5)
与短时傅立叶变换只有唯一的基函数不同,小波变换的小波基可以根据不同的需要而构造,这点使小波变换在时频分析方面具有很大的优势,对于不同的信号构造不同的基函数,使小波变换对分析信号具有足够的适应性。但小波基一经选定,在整个变化过程中不能改变。也许选择的小波基对于整个信号来说,是最优的,但是对于局部来说可能分析效果就不好了。如何进行小波基的选择是信号分析中的一个难点。采用不同的小波基对同一个信号进行分析,其结果会因小波基的不同而大相径庭,从而不具有可比性。
2.3.3 希尔伯特变换
基于经验模态分解(EMD)的希尔波特(Hibert)变换[30]也是一种时频分析方法,这种变换方法的基函数并不需要事先设定,变换方法本身使得变换过程根据信号的局部特征自动选择基函数,这一特性使得该方法特别适合非线性、非平稳信号的分析。
2.4 互信息分析
互信息是信息论中的重要概念,它可以用来度量两个通道的脑电信号之间的相互依赖程度,从信息论的角度讲,互信息就是一种信息熵,互信息理论来源于香农信息论基本原理。互信息分析相比于时频分析中的小波变换和基于经验模态分解的希尔伯特变换法,特征向量的维数较小且相关性较弱,这有利于后期分类器的设计。Elisa Carlino[31]等人利用互信息分析方法,研究精神分裂症患者与正常人在睁眼和闭眼时大脑各区域之间脑电信号的关联程度,可以非常容易的看出精神病患者和正常人之间的差别。
2.5 因果性分析
因果性分析与互信息分析相比,不仅可以分析信号的同步性,还可以分析信号的因果性,如两个脑区之间的脑电活动之间的具体联系。因果分析能表征出信息流方向或者因果关系。常用的因果性分析方法有:格兰杰因果性[32]、有向相干性[33]、部分有向相干性[34]和非线性因果性[35]。
2.6 复杂度分析
的专家学者开始分析正常人与患者之间生物电信号方面的差别,如肌电信号、脑电信号等方面。肌电信号包含了反映运动模式和运动意愿的丰富信息[17]。基于对肌电信号的分析,可以直接对外周神经细胞、肌纤维、神经肌肉接头等处的功能情况进行评估。Ei-Abd等人[18]在研究脑损伤患者和正常人肘关节屈伸运动时的肌电信号变化中发现,58%的脑损伤患者的上肢有主动肌和拮抗肌同时收缩;当肘关节快速运动时,正常人有3相肌电活动,而脑损伤患者中66%呈主动肌持续性电活动。季林红等人[19]采用基于自适应Chirplet 分解的时频分析方法,对15例偏瘫患者在完成快速伸肘过程中肱二头肌的肌电信号进行分析,利用最优Chirplet 时频参数对脑损伤导致的肌强直症状进行定量评估。研究结果表明基于肌电信号Chirplet时频参数的功能评价与相应的简式Fugl-Meyer功能评价存在较好的线性关系。
Fu[20]等人以7个健康人和11个脑卒中患者为研究对象,就由于脑损伤导致上肢运动功能障碍患者,能否通过想象患肢的动作使EEG的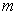 节律出现ERD特征模式进行了对比实验研究。实验结果显示在脑部运动控制功能障碍患者的EEG中仍可以侦测到 节律出现ERD特征模式进行了对比实验研究。实验结果显示在脑部运动控制功能障碍患者的EEG中仍可以侦测到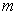 节律的ERD特征模式,不过其ERD的峰值明显比健康人的低;Berardelli 等[21],用电刺激运动皮层后,发现脑卒中患者MEP消失,中枢运动潜伏期延长。Heald等[22]研究发现,中风发作后72小时检测的中枢性运动传导时间(Central motor conduction time,CMCT)与功能预后及死亡率密切相关。国内外众多专家学者对大脑与肌肉之间的信息传递方向进行研究。Ferruccio Panzica[23]等人利用部分直接相干法分析癫痫患者脑电信号与肌电信号的关联程度,研究发现癫痫患者与健康人相比,癫痫患者的信息传递较为紊乱,既有大脑流向肌肉的信息传递,也有较强的信号是从肌电信号传向脑电信号。类似的,Tatsuya Mima[24-25]等人也做过这方面的研究。 节律的ERD特征模式,不过其ERD的峰值明显比健康人的低;Berardelli 等[21],用电刺激运动皮层后,发现脑卒中患者MEP消失,中枢运动潜伏期延长。Heald等[22]研究发现,中风发作后72小时检测的中枢性运动传导时间(Central motor conduction time,CMCT)与功能预后及死亡率密切相关。国内外众多专家学者对大脑与肌肉之间的信息传递方向进行研究。Ferruccio Panzica[23]等人利用部分直接相干法分析癫痫患者脑电信号与肌电信号的关联程度,研究发现癫痫患者与健康人相比,癫痫患者的信息传递较为紊乱,既有大脑流向肌肉的信息传递,也有较强的信号是从肌电信号传向脑电信号。类似的,Tatsuya Mima[24-25]等人也做过这方面的研究。
2 基于脑电分析运动功能障碍的特征提取方法
特征提取是脑电信号处理过程中非常重要的环节,提取类别之间区分度大的特征将会大大降低特征分类的难度。特征提取是指通过一系列的映射和变换,降低原始信号空间的维数,使得一些能反映事物特点的,但不易通过观察或者检测的特征从原始的特征域中显示出来。下面简单介绍几种特征提取的方法:
2.1 时域分析法
时域分析法主要是根据采集到的脑电信号(如电压信号)直接提取波形特征,比较直观。早期的脑电图分析主要采用时域分析方法。通过对脑电时域波形分析,以获取一些重要的脑电时域特征,如方差分析、直方图分析、相关分析、峰值检测和过零点检测等。Abduljalil Mohamed[26]等人将单位时间窗的多种时域特征(包括求和值、均值、标准差、过零点数和能量值)作为特征值组成特征向量,利用DS证据理论对K近邻算法进行改进,对是否患有癫痫疾病进行分类识别,取得了较好的实验结果。
时域分析方法由于提取的特征过于简单,且含有较多的噪声,已经很少被使用。但是由于该方法算法简单,计算量小,对于提高脑电信号的处理效率依然具有参考价值。
2.2 频域分析法
频域分析主要是利用傅立叶变换,将原始的时域信号转换到频域中,提取频域中的特征。频域分析方法主要是EEG的功率谱估计,把幅度随时间变化的脑电波变换为脑电功率随频率变化的谱图,可以直接观察EEG中的β、α、δ、θ等节律的分布与变化情况。常用方法有功率谱估计、AR模型功率谱估计、双谱分析[27]等。这类方法简单,使用较多。但是信息单一,对于非平稳性很强的自发EEG来说,识别精度比较低,但比较是适用于较为简单的BCI系统中两种思维任务的分类。Junhua Li[51]等人利用Lomb-Scargle谱分析法对运动想象的脑电信号进行特征提取,再利用支持向量机(SVM)和Denoising Autoencoder(DEA)法进行模式分类对比分析。Lomb-Scargle谱分析法相比于传统的功率谱估计法,在对分类结果没有造成显著影响的情况下,可以大大缩短EEG信号的长度。
2.3 时频域分析
时频分析方法可以得到时-频谱,我们可以得到在整个时间段内的每一个时刻的频律成份分布情况,也可以得到频率成分随时间的变化情况。这就给我们分析非线性、非平稳的信号提供了有力的工具。目前较常见的时频分析方法有:短时傅立叶变换,小波变换,Wigner-Ville分布[28]等[29]。
2.3.1短时傅立叶变换
短时傅立叶变换是将非平稳信号假设成分段平稳,通过一个固定长度的滑动窗,分段的截取信号,并对所截取的信号进行傅立叶变换。这样就可以得到信号x(t)在任意时刻的频谱。
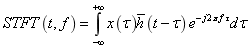 (1) (1)
其中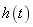 为窗函数, 为窗函数,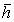 为窗函数的共轭。短时傅立叶变换的模值的平方,称为谱图Spectrogram(SPEC),它表示能量随时间和频率的分布状况。 为窗函数的共轭。短时傅立叶变换的模值的平方,称为谱图Spectrogram(SPEC),它表示能量随时间和频率的分布状况。
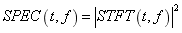 (2) (2)
短时傅立叶变换的主要缺陷是窗口长度求解前需固定,不能随着信号分析需要进行而调节。根据Heisenberg测不准原理,短时傅立叶变换时频表示的时间分辨率和频率分辨率是相互矛盾的不可能在时间和频率两个方向同时获得高的分辨率。
2.3.2小波变换
小波变换克服了短时傅立叶变换窗口长度固定,不能满足不同频率需要不同分辨率的要求的缺点,时间窗长度可随需要不同而改变。小波变换是假设信号中频率高低不同的分量具有不同的时变特性,频率较低成分频谱随时间变化的较慢,频率较高成分频谱随时间变化快。根据上述条件,对时间轴和频率轴进行调整,通过刻度的非均匀划分,达到获得较好时频分辨率的目的。
信号x(t)小波变换的定义式为:
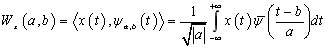 (3) (3)
式中,a为尺度因子,b为平移因子,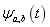 为小波基函数,是小波基 为小波基函数,是小波基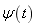 经过平移和伸缩得到的。 经过平移和伸缩得到的。
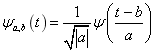 (4) (4)
小波变换的系数幅平方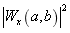 被称为小波谱,它属于仿射类时频表示。将 被称为小波谱,它属于仿射类时频表示。将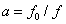 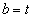 代入可得到小波变换的时频表示: 代入可得到小波变换的时频表示:
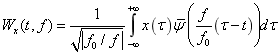 (5) (5)
与短时傅立叶变换只有唯一的基函数不同,小波变换的小波基可以根据不同的需要而构造,这点使小波变换在时频分析方面具有很大的优势,对于不同的信号构造不同的基函数,使小波变换对分析信号具有足够的适应性。但小波基一经选定,在整个变化过程中不能改变。也许选择的小波基对于整个信号来说,是最优的,但是对于局部来说可能分析效果就不好了。如何进行小波基的选择是信号分析中的一个难点。采用不同的小波基对同一个信号进行分析,其结果会因小波基的不同而大相径庭,从而不具有可比性。
2.3.3 希尔伯特变换
基于经验模态分解(EMD)的希尔波特(Hibert)变换[30]也是一种时频分析方法,这种变换方法的基函数并不需要事先设定,变换方法本身使得变换过程根据信号的局部特征自动选择基函数,这一特性使得该方法特别适合非线性、非平稳信号的分析。
2.4 互信息分析
互信息是信息论中的重要概念,它可以用来度量两个通道的脑电信号之间的相互依赖程度,从信息论的角度讲,互信息就是一种信息熵,互信息理论来源于香农信息论基本原理。互信息分析相比于时频分析中的小波变换和基于经验模态分解的希尔伯特变换法,特征向量的维数较小且相关性较弱,这有利于后期分类器的设计。Elisa Carlino[31]等人利用互信息分析方法,研究精神分裂症患者与正常人在睁眼和闭眼时大脑各区域之间脑电信号的关联程度,可以非常容易的看出精神病患者和正常人之间的差别。
2.5 因果性分析
因果性分析与互信息分析相比,不仅可以分析信号的同步性,还可以分析信号的因果性,如两个脑区之间的脑电活动之间的具体联系。因果分析能表征出信息流方向或者因果关系。常用的因果性分析方法有:格兰杰因果性[32]、有向相干性[33]、部分有向相干性[34]和非线性因果性[35]。
2.6 复杂度分析
当以色列数学家Lempel和Ziv[36]给出复杂度的具体计算方法后,复杂度这一非线性特征由于其自身特点受到广泛关注。LZC是从一维的角度反映时间序列,与EEG的分形维数分析方法相比,复杂度分析的物理意义更明确,所需数据更短,计算速度更快,是应用非线性动力学探索大脑功能和诊断疾病的又一途径。X.S.Zhang[37]等对27例血管外科手术患者进行了脑电复杂度分析的麻醉深度监测研究,发现复杂性测度性能(93%)较其他诸如近似熵(89%)、谱熵(76%)和中心频率(64%)更高,而且复杂性测度只需较短的EEG时间序列,大概是近似熵所需时间的1/50。
3 基于脑电信号的运动功能障碍评估分类方法研究
3.1 分类器设计
模式识别的目的是确定某一给定信号属于哪一类,这可通过将被识别对象的多种特征参数构成特征矢量,并将其作为某一判决方程的输入,根据输出来判断该识别对象的类型。为了得到判决方程,一方面要有判决规则,另一方面要有一定数量的样本值作为标准。在脑电分类方法上,贝叶斯分类器、聚类方法、神经网络等都有广泛应用。
3.1.1 线性分类法
在线性判别分析中,首先为每一类建立概率密度模型,假定每一类的概率密度函数都可以用一个标准的密度函数模型表示,并且这个密度函数对所有的类具有相同的协方差。在此基础上,对每个新输入的特征数据计算每一类产生的概率,根据各类概率的大小来判断所属的类别。概率值最大的点对应的类别就是输入特征数据的类别。这个翻译算法是线性的,具有较好的泛化能力和稳健性。Schloegl等人最早使用线性判别分析对特征信号分类,取得了较好的分类效果。线性分类器简单、容易实现、需要的计算量和存储量小。任亚莉[38]等人提出时变线性分类器的概念理论,非常适合非线性时变的脑电信号分类。
3.1.2 决策树
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。决策树是由一系列节点组成的,每一个节点代表一个特征和相应的决策规则。决策树的构建过程就是选取特征和确定决策规则的过程。黄玲[52]等人将决策树与支持向量机相结合,用类分布的可分离性测度来决定决策树走向,成功将运动想象左手运动与右手运动产生的脑电信号进行分类识别,识别精确度高达80.8%。决策树分类器适合多类别的识别分类。
3.1.3 聚类分类法
这是一种线性方法。其算法原理简单,运算速度极快。在用于肌电信号的识别中,对于不同类别重叠区小、差异明显的特征,我们采用这种分类发。它不仅对信号的实时分析十分有利,而且分类前只需简单计算部分样本的均值和方差,避免了许多非线性分类法冗长的训练过程。当然,聚类分类法也有很大的不足:它对肌电特征的要求较高,由于是线性分类器,处理较复杂的问题困难,容易导致分辨率降低。
3.1.4人工神经网络法
人工神经网络(Artificial neural networks, ANN)是一种比较好的机器学习方法,它的一个重要特点是能够较有效地解决很多非线性问题,而且在很多工程应用中取得了成功。人工神经网络是BCI系统应用最多的分类器, 由于其应用简单, 参数选择方便, 分类结果准确性较高, 被广泛地应用于脑电信号的分类。神经网络大致分为前向网络、反馈网络、自组织网络和随机网络4大类。用于模式识别分类的神经网络类型比较多, 主要为感知器、多层感知器、径向基函数网络、BP 网络等。神经网络在信号处理、模式识别、脑电、诱发电位等生物医学信号处理方面有较多的应用。
实际应用中,Anderson等[39]用多变量的AR模型提取EEG特征,并用前向型神经网络对4个人五种认知状态下的EEG进行分类,准确率为38%︿71%;利用前馈神经网络进行意识任务进行分类,分类正确率高达91.4%;Pfurtscheller等[40]利用神经网络分类器对手运动进行在线分类的研究,试验结果表明:对于2种不同的运动下EEG模式,其最好的分类结果是87%。
3.1.5 支持向量机
支持向量机(SVM)是在统计学习理论的基础上发展起来的新一代学习算法[49],由于其出色的学习性能,该技术己经成为机器学习界的研究热点,并在很多领域尤其是模式识别领域得到了成功的应用。SVM与基于经验风险最小化原则的传统分类器相比,不仅结构简单,而且各种性能尤其是推广能力明显提高。它基于结构风险最小化原则,具有严格的理论基础,能较好地解决小样本、非线性、高维数和局部极小点等实际问题,已经成功应用于模式识别各个领域中的分类和回归[41-42]。
3.2 信息融合决策理论
信息融合一般是指将来自不同传感器的信息进行有效合成的技术[43]。进行融合的目的是为了获得比单源信息更加全面的结果。随着信息技术的发展,更多信息融合的算法被提出,均在不同领域发挥了重要作用[50]。按照算法处理的基本方法,可将多源数据融合分成随机和人工智能两类。随机类算法有KALMAN滤波法、D-S证据理论等。人工智能类算法有模糊逻辑理论、神经网络等。虽然融合的算法多种多样,但是信息融合的三个本质特征却是不变的。它们分别是:多源信息的输入、信息的有效融合和根据融合结果的决策。
Dempster于1967年最先提出证据理论,后经过其学生Shafer进一步发展完善,才形成了相对成熟的D-S证据推理。它是一种针对不确定问题的推理方法,核心是Dempster合成法则,重点任务在于构造正确的证据模型和确定合适的判定决策。D-S证据理论的一个特点是能进行信息不确定性推理[44]:将得到的信息作为证据,在决策目标集上建立一个相应的基本可信度。这样,证据理论能在同一决策框架下,用Dempster合并规则将不同的信息合并成一个统一的信息表示。D-S证据理论允许直接将可信度赋予传感器信息的核取[45],既避免了对未知概率分布所作的简化假设,又保留了信息。
近年来,D-S证据理论在EEG信号处理中得到广泛的应用。如利用D-S证据理论对SVM的分类识别结果进行融合[46-47]。Abduljalil Mohamed[26]、Ashkan Yazdani[48]等研究团队将D-S证据理论与K近邻分类器相结合,将K个近邻的选择进行不确定性模糊化处理。两者结合之后,在使用较为简单的时域特征的情况下,可以得到较好的分类结果。
总结:
现在,人们对自己的生命健康越来越关注,也迫切的希望了解人体的生理特征。从脑电信号等生物电信号的角度出发,研究人类运动功能障碍是一个非常好的切入点。目前,虽然脑电信号的特征提取与识别方法很多,但基本都有其自身的局限性。根据分析患者产生的病理波与健康人的脑电波之间的差异提取合适的特征,并设计分类器是本文研究的重点内容。本文研究的预期目标是能够实现利用实现根据脑电信号对人体运动功能障碍进行分级评估。
参考文献
[1] 林平光, 叶宁国, 阎丽. 虚拟现实技术应用于认知康复领域的国际研究综述[J]. 医疗保健器具, 2007 (5): 13-14.
[2] 龚文青, 诸强. 虚拟现实技术应用于运动障碍康复的研究[J]. 生物医学工程学进展, 2009 (4): 238-241.
[3] 张丽霞,王彤. 中枢神经损伤性运动障碍的评估(评估量表的临床应用)[J].中国康复医学杂志, 2005,20(8):627-629.
[4] J. Sanford, J. Moreland, L. R. Swanson, et al. Reliability of the Fugl-Meyer assessment for testing motor performance in patients following stroke[J].Phys Ther,1993, 73(2):447-454.
[5] S. Lennon, A. Ashburn, D. Baxter. Gait outcome following outpatient physiotherapy based on the Bobath concept in people post stroke [J]. Disability and Rehabilitation, 2006, 28(13-14): 873-81.
[6] S. W. Chou, A. M. Wong, C. P. Leong, W. S. Hong, F. T. Tang, T. H. Lin. Postural control during sit-to stand and gait in stroke patients [J]. Archives of Physical Medicine and Rehabilitation, 2003, 82(1): 42-7.
[7] 王煜, 于涛. 针刺治疗脑卒中后患者偏瘫步态疗效观察[C]. 2010年中国针灸学会学术大会论文集, 2010, 21(3): 313-317.
[8] K. A. Hughes, F. Bell. Visual assessment of hemiplegic gait following stroke: pilot study [J]. Archives of Physical Medicine and Rehabilitation, 1994, 75(10): 1100-7.
[9] 徐光青,兰月, 毛玉瑢. 脑卒中患者躯体运动偏瘫模式的三维运动学评价[J].中国康复医学杂志, 2009, 24(10) : 893-895.
[10] H. Zheng, N. D. Black, N. D. Harris. Position-sensing technologies for movement analysis in stroke rehabilitation[J]. Medical &Biological Engineering &Computing, 2005, 43(4): 413-20.
[11] 刘楚红. 基于 FSR 和陀螺仪的人体姿态检测及行走趋势分析[D]. 沈阳工业大学, 2015.
[12] H. Zheng, R. Davies, T. Stone et al.. SMART rehabilitation: implementation of ICT platform to support home-based stroke rehabilitation[C]. Lecture Notes in Computer Science, 2007, 4554: 831-840.
[13] A. Karlsson, G. Frykberg. Correlations between force plate measures for assessment of balance [J]. Clinical Biomechanics, 2000, 15(5): 365-9.
[14] A. J.Orrell, F. F.Eves, R. Masters. Motor learning of a dynamic balancing task after stroke: implicit implications for stroke rehabilitation. Physical Therapy, 2006, 86(3):369–380.
[15] 许光旭,王彤, 王翔. 偏瘫的不对称步态的生物力学研究[J]. 中国康复医学杂志, 1995, 10(3): 97-101.
[16] M. J. Lomaglio, J. J. Eng. Muscle strength and weight-bearing symmetry relate to sit-to-stand performance in individuals with stroke [J]. Gait Posture, 2005, 22(2): 126-131.
[17] R.N. Scott, P.A. Parker. Myoelectric prostheses :State of the art[J]. Journal of medical engineering &technology, 1988,12(4):143-151.
[18] M.A. Ei-Abd, I.K. Ibrahim. Impared activation pattern in antagonistic elbow muscles of patients with spostic hemiparesis contribution to movement disorder [J]. Electromyogr Clin Neurophysiol, 1993, 33(4):247-255.
[19] 季林红,张宇博, 王子羲等.基于自适应Chirplet分解的偏瘫肌强直症状评估[J].清华大学学报(自然科学版), 2007,47(5):627-630.
[20] Fu J. Michael, Daly J.Janis, M. Cenk Cavusoglu. Assessment of EEG event-related desynchronization in stroke survivors performing shoulder-elbow movements[C]. Proceedings of the 2006 IEEE International Conference on Robotics and Automation Orlando, 2006: 3158-3163.
[21] A. Berardelli, M. Inghilieri, M. Manfredi.. Cortical and cervical stimulation after hemispheric infarction[J]. J. Neurol Neurosurg Psychiatry, 1987, 50(3):861-865.
[22] A. Heald, D. Bates, N.E. Cartlidge, et al.. Longitudinal study of central motor conduction time following stroke: Central motor conduction measured within 72h after stroke as predictor of function outcome at 12 months[J].Brain,2003,116(2):1371.
[23] Panzica F, Canafoglia L, Franceschetti S. EEG–EMG information flow in movement-activated myoclonus in patients with Unverricht–Lundborg disease[J]. Clinical Neurophysiology, 2014, 125(9): 1803-1808.
[24] Mima T, Toma K, Koshy B, et al. Coherence between cortical and muscular activities after subcortical stroke[J]. Stroke, 2001, 32(11): 2597-2601.
[25] Mima T, Matsuoka T, Hallett M. Information flow from the sensorimotor cortex to muscle in humans[J]. Clinical Neurophysiology, 2001, 112(1): 122-126.
[26] Mohamed A, Shaban K B. Effective seizure detection through the fusion of single-feature enhanced-k-NN classifiers of EEG signals[C]//Biosignals and Biorobotics Conference (BRC), 2013 ISSNIP. IEEE, 2013: 1-6.
[27] 许崇涛, 沈民奋, 李慧, 朱国平. 双谱分析方法在脑电信号分析中的应用[J]. 中国行为医学科学. 2004, 3: 340-341.
[28] Wigner EP.On the Quantum Correction for Thermodynamic Equilibrium[J]. Physical Review, 1932,40:749~759.
[29] Ristic B, Boashash B. Instantaneous frequency estimation of quadratic and cubic FM signals using the cross polynomial Wigner-Ville distribution[J]. IEEE Signal Processing Society. 1996, 44(6): 1549-1554.
[30] Huang NE,Shen Z,Long SR,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.of the Royal Society of London,1998,454:903~995.
[31] Carlino E, Sigaudo M, Rosato R, et al. Electroencephalographic connectivity analysis in schizophrenia[J]. Neuroscience letters, 2015, 604: 145-150.
[32] Pincus S M,Goldberger.Physiological time-series analysis: What does regularity quantify [J].American Journal of Physiology – Heart and Circulatory Physiology,1994,266(435-4): 1643-1656.
[33] Richman J S,Moorman J R.Physiological time-series analysis using approximate entropy and sample entropy[J].American Journal of Physiology-Heart and Circulatory Physiology,2000,278(6): H2039-H2049.
[34] Christoph Bandt,Bernd Pompe.Permutation entropy — a natural complexity measure for time series[J].Physical review letters,2002,88(17): 1-4.
[35] Chavez M,Martinerie J, Le Van Quyen M. Statistical assessment of nonlinear causality:application to epileptic EEG signal. J Neurosci Meth, 2003,124(2):113-128.
[36] Lempel A, Ziv J. On the complexity of finite sequences[J]. Information Theory, IEEE Transactions on, 1976, 22(1): 75-81.
[37] Zhang X S, Roy R J, Jensen E W. EEG complexity as a measure of depth of anesthesia for patients[J]. Biomedical Engineering, IEEE Transactions on, 2001, 48(12): 1424-1433.
[38] 任亚莉. 基于功率谱熵和频带能量的运动意识任务分类研究[J]. 计算机应用与软件, 2010, 27(12): 105-107.
[39] Anderson CW, Stolz EA, Sham SS. Multivariate autoregressive models for classification of spontaneous electroencephalographic signals during mental tasks. IEEE Transactions on Biomedical Engineering,1998,45(3):277-286.
[40] Pfurtscheller G, Kalcher J, Neuper Ch, el. On-line EEG classification during externally paced hand movement using a neural network based classifier. Electroenc ephalography& Clinical Neurophyisology,1996,99(5):416-425.
[41] 罗志增, 周镇定, 周瑛, 等. 双树复小波特征在运动想象脑电识别中的应用[J]. 传感技术学报, 2014, 27(5): 575-580.
[42] 徐琦, 王永骥, 周慧, 等. 支持向量机方法在运动意识识别中的应用[J]. 华中科技大学学报: 自然科学版, 2008, 36(6): 93-95.
[43] Hui Luo, Youren Wang, Hua Lin. Information fusion feature preprocessor based on FRFT for analog circuits fault diagnosis[C]. The 10th International Conference on Electronic Measurement & Instruments (ICEMI), Chengdu, China, 2011, 4: 132-137.
[44] 罗志增, 叶明. 用证据理论实现相关信息的融合[J]. 电子与信息学报, 2001, 23(10): 970-974.
[45] Klein L A. Sensor and data fusion concepts and applications[C]. Society of Photo-Optical Instrumentation Engineers (SPIE), 1993.
[46] LIN Chun-fu,WANG Sheng-de.Fuzzy support vector machines[J].IEEE 3(2): 464-471.
[47] Ameri A, Kamavuako E N, Scheme E J, et al. Support vector regression for improved real-time, simultaneous myoelectric control[J]. Neural Systems and Rehabilitation Engineering, IEEE Transactions on, 2014, 22(6): 1198-1209.
[48] Yazdani A, Ebrahimi T, Hoffmann U. Classification of EEG signals using Dempster Shafer theory and a k-nearest neighbor classifier[C]//Neural Engineering, 2009. NER'09. 4th International IEEE/EMBS Conference on. IEEE, 2009: 327-330.
[49] Lin H T, Lin C J, Weng R C. A note on Platt’s probabilistic outputs for support vector machines. Machine Learning, 2007, 68(3):267-276.
[50] 王耀南, 李树涛. 多传感器信息融合及其应用综述[J]. 控制与决策, 2001, 16(5): 518-522.
[51] Li J, Struzik Z, Zhang L, et al. Feature learning from incomplete EEG with denoising autoencoder[J]. Neurocomputing, 2015.
[52] 黄玲, 张爱华. 改进的决策树 SVM 在脑电识别中的应用[J]. 计算机工程与设计, 2010 (2): 382-384.
学生(签字):
年 月 日
|



