Belotti, F., G. Ilardi, 2017, Consistent inference in fixed-effects stochastic frontier models. Journal of Econometrics, forthcoming.

Emvalomatis, G., 2012, Adjustment and unobserved heterogeneity in dynamic stochastic frontier models. Journal of Productivity Analysis 37, 7-16.

Feng, G., A. Serletis, 2009, Efficiency and productivity of the US banking industry, 1998–2005: Evidence from the Fourier cost function satisfying global regularity conditions. JOURNAL OF APPLIED ECONOMETRICS 24, 105-138.

Tsionas, E.G., 2006, Inference in dynamic stochastic frontier models. JOURNAL OF APPLIED ECONOMETRICS 21, 669-676.

NOTES

刘韶彧

（一）动态SFA综述

非效率项为何具有动态特征？参见(Belotti and Ilardi, 2017), Section 4.2。

现实中，当期效率较高的公司在下一期仍然可能为维持较高的效率。基于这一思路，(Feng and Serletis, 2009), Desli, Ray and Kumbhakar(2003), Tsionas(2006), (Emvalomatis, 2012)等学者提出了动态SFA模型，基本思想是假设非效率项为AR(1) 过程，即本期的非效率程度受到上一期非效率水平的影响。以Ahn and Sickles(2000)的设定为例：

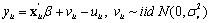
非效率项设定为：

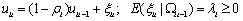
其中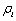，用于衡量第i家公司对非效率项的调整能力(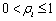)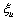，为非负的干扰项(iid)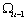，表示在第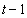期能够获得所有信息集。这里允许不同的公司具有不同的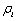和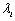，以反映公司在生产和管理方面的异质性。上述设定的含义在于，在第t期期初，公司已经了解到其上期的无效率水平(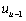)，并采取措施改善了部分无效率(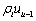)。因此，该公司当前的无效率水平由两部分组成：上一期无效率项中尚未调整的部分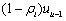和本期新来的未预期到的非效率干扰。

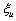若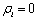，则表明该公司的无效率值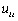服从一个单位根(unit root)过程，等于以往各期的干扰项(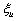)的加总。也就是说，随着时间的推移，此类公司的无效率值会变得无穷大，从而使此类公司无法在竞争性的行业中长期存在。此外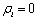，也意味着该公司的产出水平是非平稳序列。简言之，时公司对其无效率行为没有任何调整能力。若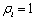，则表明公司能完全调整上一期的非效率项。显然，多数情况下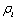，的取值都是介于0和1的，其值越大表明公司对非效率的调整能力越强。

（二）美国银行效率，动态SFA，(Tsionas, 2006)

研究了128家美国大型银行在1989-2000年期间的效率。结果表明，使用动态SFA模型估计出的效率比静态SFA模型估计出的效率高了6.5%。这表明美国大型银行都是非常有效率的。更为重要的是，他们发现 的估计值非常接近于0，意味着那些微小的非效率损失具有时序上的持续性(persistence)，短期内很难进一步降低。缺点在于方法过于复杂，可用两步估计法替代（关键在于，是否有人已用过两步估计的动态sfa方法测算中国银行效率）。

大多数SFA模型没有注意到的假设：一个公司如果长期保持技术效率低下，则会被淘汰。如果技术效率低下是由公司影响的因素造成的，但是这些因素不能在没有成本的情况下进行调整，那么效率的提高必然取决于调整的成本。如果这样的成本很高，我们预计会发现持续的技术效率低下。

遗漏动态模型的原因：（1）似然函数的复杂性（2）对未观察到的公司特定的无效率的推断非常难，数据通常不会提供太多的帮助，因此研究员通常偏向于设定较为简单的假设（which also allows “borrowing of strength”），如不随时间变化的无效率项

数据：1989-2000年128美国商业银行面板数据

模型（方法过于复杂）：在随机边界模型的基础上构建动态随机边界模型，从而衡量over time的技术无效率。使用Markov连锁蒙特卡罗技术来推断参数和无效率项（on a firm-specific basis）。

面板数据的产出边界：

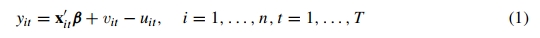
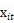是一个k*1的向量型的自变量，是k*1的向量型参数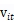，是一个双边的测量随机干扰项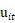，是一个非负的反映技术无效率的残差。两个残差项互相独立，同时独立于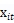，如果用的是成本边界而不是产出边界，那么x和y的符号会相反（为什么？）。

对残差项的定义如下：

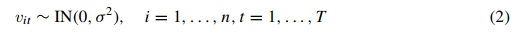
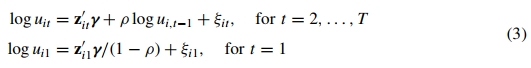
对于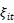，对于i=1,…,n，t=2,…,T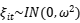，，而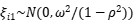（为什么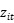？）。是一个m*1向量的协变量（相比Ahn and Sickles(2000)多增加了控制了影响非效率的外生变量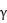），是一个m*1向量的参数，两个残差项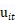和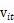互相独立，同时独立于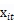和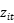。式（3）的特点在于，无效率项的过去的数值决定了，系统性的部分即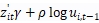反映了预期的对数无效率项，而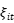则反映了不可观测因素导致的非效率留存。同时假设所有的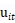源于同样的过程。当相关系数为0时，就变成了Battese and Coelli (1995) and Kumbhakar et al. (1991)的例子。需要注意的是，当T比较小时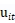，的边际分布会十分不同，因此这个模型更适合于更长期的模型。

当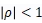时（即效率有改善的情况下），的（导致下期无效率的）过程是固定不变的。在不实质性影响方法的基础上，可以增加额外的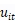的滞后项，在某种意义上于dynamic latent variable models 如stochastic volatility model (Jacquier et al., 2002; Steel, 1998)类似，对于此类模型，由于高维积分的参与，可能不存在似然函数的闭合形式表达式。

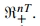通过（3）来求得式（1）结构参数变量如下：另外，潜藏变量u有明显的符号，定义为。考虑联合概率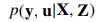，其中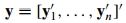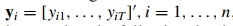，，x和z同理。计算可得：

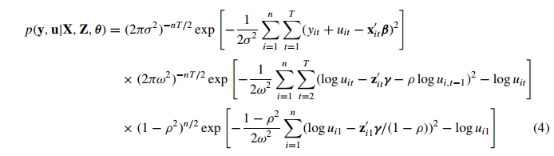第一行源于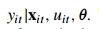的正态分布，第二行源于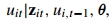的对数正态分布，第三行来源于对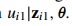的对数正态分布的假设（这个模型好复杂啊……）

需要估计的函数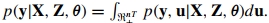： 当n或T很大时，这个积分不能被计算出来，它是非常高维的。这里，我们建议使用贝叶斯技术和MCMC方法来实现它们。另一种方法是使用最大模拟可能性的方法。

接下来介绍了贝叶斯技术和MCMC（略）

实证分析

这项研究的数据来自于由芝加哥联邦储备银行管理的商业银行和银行控股公司数据库，它基于对所有向联邦储备银行和联邦存款保险公司报告的美国商业银行的状况和收入报告，选取了在存续期内至少三年资产超10亿美元的128家大银行作为对象。

之前基于成本函数估计银行效率的研究（Berger and Humphrey, 1991）集中在技术的无效率上，在此之后，银行被视为将各种金融和实物资源转化为贷款和投资的中间渠道。 output variables：

installment loans (to individuals for personal/household expenses) y1

real estate loans y2

business loans y3

federal funds sold and securities purchased under agreements to resell y4,

other assets (assets that cannot be properly included in any other asset items in the balance sheet) y5

The input variables:

labour x1

capital x2

purchased funds x3

interest-bearing deposits in total transaction accounts x4

interest-bearing deposits in total non-transaction accounts x5

输入变量的价格总是等于总费用除以相应的数量。如the price of labour:w1=expenses on salary and benefits/the number of full time employees（x1），相同的可以得到w2→w5，所有的成本被定义为这五项之和。为了加上线性同质性的限制，我们将总成本和所有价格都基于w5标准化了。使用了超越对数函数的形式Q=5个output和M=4个input。

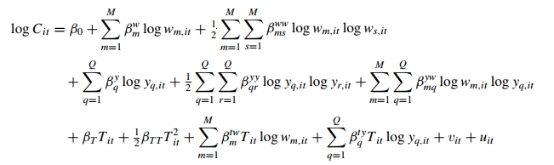
其中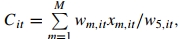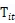：，表明一个时间趋势的变量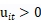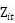，，则记录了资产及其平方的对数（规模效应对于解释技术无效率也很有帮助）。关于先验假设：针对一阶导数的相对价格系数先验的均值被设定为0.2，精确度为1，其余更高阶导数相对价格系数先验均值设定为0，精确度为0.001（这个模型好复杂啊……）

对的估计揭示规模是技术效率低下的一个重要决定因素，随着美国大型银行的总资产价值的增加，这种效率在降低，资产的平方对无效率的影响可能没有。而的估计接近0.99，证明，意味着那些微小的非效率损失具有时序上的持续性(persistence)，短期内很难进一步降低。

文章解释，动态SFA模型估计出的效率比静态SFA模型估计出的效率高了6.5%。这表明美国大型银行都是非常有效率的。

（三）中国银行的风险承担与效率，动态SFA（谭政勋、李丽芳，2016）

主要研究的是风险承担与效率的关系，对效率的变化没有着重研究，使用方法主要是异方差非单调效率测算模型（动态sfa+异方差设定），得到效率结果后，来判断效率的改进；我们是否可以用两步估计法来分析效率改进（创新点在于方法？），用来研究银行的效率，或者来研究上市金融控股公司的效率（通过变更投入产出来研究成本和利润效率）

研究主题：从货币政策的宏观角度来研究我国商业银行风险承担与效率的关系

模型设定：无效率项非单调变化且存在异方差的随机前沿模型

本文综合三种将风险因素引进模型方法， 力图准确测算银行效率及影响因素：首先， 把权益资本引进前沿生产函数， 直接考察风险态度对效率的影响；其次， 为了深入考虑风险承担对银行效率的影响， 参照第二种方法， 本文把流动性风险即贷存比和综合风险 Z 值作为无效率项的解释变量。最后， 由于第二种方法不能从动态的角度考察银行风险承担对效率的影响， 尤其是不能深入分析货币政策、 商业银行风险承担与效率的复杂关系， 所以本文还将采用第三种方法即两阶段估计法（采用前沿函数先估计出无效率项，然后分析银行风险承担对效率的影响）。

1、效率测算模型与投入产出指标

本文采用允许存在异方差和非单调的效率测算模型( Wang，2002)，放松了无效率项随时间单调变化的假设， 又同时对无效率项的均值和方差建立回归方程。

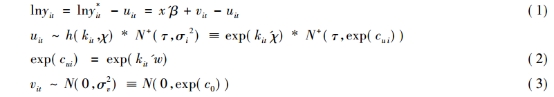
式( 2) 允许无效率项存在异方差， 并且 k对无效率项均值的影响是非单调的， 即在整个样本内部， k对效率的影响可能为正或为负， 取决于 k的具体取值。 如果式( 1) 中 y 表示利润， 则公式不变; 如果 y 表示成本， 则式( 1) 中的 －u变为 u。

投入：式中三个投入指标与多数文献一样， 它们是可贷资金成本( w1) 、 劳动力和固定资产投入价格( w2) 以及净投入即权益资本; 由于缺少独立的劳动力数据( 如人员费用) ， 参照Hasan and Marton( 2003) 、 姚树洁等( 2011) 的方法， 将劳动力和实物资本的价格定义为非利息支出占总资产的比例。在投入价格的处理上， Patti and Hardy( 2005) 、 姚树洁等( 2011) 指出， 如果使用各银行本身的要素支出除以全部要素投入来得到银行各自的要素价格， 使得要素投入价格具有很强的内生性， 违背了成本和利润函数中要素投入价格外生性的假设条件。借鉴他们的做法， 模型中 wi 是市场平均投入要素价格， 即除被测算的银行外的其他银行的投入要素的平均价格， 这既符合外生性条件， 又能提高估计结果的可靠性

产出：首先定义三种产出， 它们是贷款、 非利息收入和存款( 记为组合 1) 。其次， 由于样本期间的早期， 中国银行业尤其是四大银行的不良贷款率很高， 所以借鉴 Sun and Chang ( 2011) ， 总贷款减去不良贷款的净贷款视为产出， 其他两个指标不变( 记为组合 2) 。最后， 把两个产出组合所测算的效率进行对比。

2、银行效率与风险承担的关系模型

格兰杰因果法的动态面板模型来分析风险与效率的关系

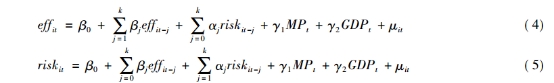
模型( 4) 和( 5) 中， 除本文需要重点考察的银行风险承担、 效率和货币政策外， 包括 2类控制变量: (1)银行特征变量 (2)宏观变量

银行风险承担risk变量包括：（1）市场风险：股票价格及其收益率的波动( Sun and Chang，2011)，对非上市银行不可行；（2） 经营风险：破产概率即 Z 值Z = σ( ROA) /( ROA + CAR)，采用 Z 值来衡量经营风险， 把资产回报率的波动率作为稳健性检验（3）信用风险变量：不良贷款率来衡量信用风险并进行稳健性检验

货币政策代理变量：商业银行是货币政策调控宏观经济的主要载体， 尤其是国有银行经历了 1998－1999年的注资重组、 2004－2005 年的股份制改革以及 2009－2010 年大规模的信贷投放， 其资产质量在不同时期均受到了内外部因素的威胁。引入广义货币供应量( M2) 的增长率、 贷款基准利率( 用 ir 表示) 作为货币政策的代理变量。

为了集中精力讨论银行风险承担与效率的关系， 银行特征变量只选取了银行资本水平。由于资本充足率的数据不全， 采用资本资产比来衡量银行资本水平。本文数据来自于 bankscope 和银行年报， 不良贷款的数据主要来自于施华强( 2005) ， 部分股份制银行的不良贷款是估算得到。数据年限为 1994－2013 年，共 355 个样本。

3、实证结果与分析

A.效率测算方法和结果说明

本文在国内是首次改进 Wang( 2002) 的允许存在异方差的非单调效率模型进行改进，并测算了不同产出组合、 非效率项方差不变或存在异方差等多种情况下的效率，所以对结果及其可靠性做出说明。

第一， 是否应该使用复合误差项或者非效率项在统计上是否显著? 使用似然比进行检验: 先分别估计复合误差项模型和单一误差项模型并得到两个方程的最大似然值; 然后用前者减去后者并乘以 2， 并假设该统计量服从混合卡方分布; 最后与不同显著性水平的临界值( Delis and Kouretas ( 2011) 计算和模拟了混合卡方分布的临界值) 进行对比。

第二， 假设非效率项是同方差还是异方差? 这个问题的解决分为两步， 第一步的解决办法与第一个问题类似， 先分别估计非效率项是同方差和异方差两个方程并得到它们的似然值， 然后用后者前去前者并乘以 2， 得到似然比， 最后根据混合卡方分布的临界值进行判断。第二步是判断非效率项方差的各个因素的影响是否显著， 如果至少有一个变量的影响是显著的， 则可确认存在异方差。表 1 回答了这两个问题。从表 1 的左栏可以看到， 无论是利润模型还是成本模型， LR1 大于显著水平为 0．001 的临界值， 这说明无效率项对误差项有着显著影响， 因而要采用复合误差项; LR2 也大于显著水平为 0． 001 的临界值， 因此无效率项存在异方差。其次， 两个方差方程中， 至少有三个自变量对方差的影响是显著的， 这进一步证明要使用异方差的无效率项。

B.效率的测算结果及分析

由于不良贷款是“坏产出” ， 因此对成本效率和利润效率均会产生一定影响。为此本文测算并比较如下两个组合的效率， 组合 1 为贷款、 非利息收入和存款; 组合 2 为净贷款、非利息收入和存款。其次， 考察了资本投入和不同测算方法对效率的影响。

在上述两个组合中， 计算三种情况下的效率: 一是在前沿模型中没有引进权益资本；二是引进权益资本， 并假设无效率项在不同个体间的方差相同；三是引进权益资本， 但无效率项在不同个体间的方差不一样；三种情况下的效率估计值分别记为效率 1、 效率 2 和效率 3。

结果：

不良贷款对效率影响：组合2测算的利润效率不低于1，成本效率相反，不良贷款对成本效率有着显著的膨胀效应

资本投入对效率影响：如果不考虑资本投入，无论成本效率还是利润效率，与效率2及效率3相比较，效率 1被高估；

无效率同方差与异方差两种情况比较：效率估计结果没有太大差别，即稳健性得到保证，但是异方差的假设更为合理（但如果没有差别，用同方差计算不是更容易吗？）

比较利润效率3和成本效率3（选题切入？如何有创新性）：从图 5 看， 本文测算的成本效率和利润效率的走势具有较好的吻合度， 两个效率从 1994 － 2001 年基本上是下降的， 2001 － 2004 是上升阶段， 然后比较稳定， 2009 年后处于下降阶段。这个结果与我国商业银行的经营状况、 制度改革以及外部经济环境基本一致。1995 年以来， 我国国有企业效益大幅下滑， 商业银行尤其是四大国有银行积累了大量的不良贷款， 而 1998 爆发的亚洲金融危机更是雪上加霜， 效率下降; 直至 2002 世界经济的复苏和 2003 年开始的对国有银行实施“财务重组－引入战略投资者－上市－完善治理制度” 的有史以来力度最大的一次制度改革，才使我国商业银行特别是四大国有银行的经营效益逐步得到好转，因此，银行效率在 2001 年见底后，逐步好转; 2007－2008年发生的世界金融危机对我国商业银行也产生了一定影响，利润效率、 成本效率分别从 2009 年和 2008 年开始下降。

本文与姚树洁等( 2011) 所测算的利润效率的走势基本一致， 但成本效率相差较大。

姚树洁等( 2011) 的成本效率从1995－1998是上升的， 1999－2005是下降的， 这个趋势不仅与其自身测算的利润效率刚好相反， 与本文结果也相差较大。但从随机前沿模型的测算原理来看， 采用投入模型或者产出模型所测算的成本效率和利润效率应该基本一致， 因此从这个角度并结合表1的结果，应该说本文的测算方法更为合理。

C.货币政策、 银行风险承担与效率的关系

由于采用 25 家上市银行与非上市银行的面板数据， 因而可能存在异方差和自相关;如果采用 OLS 进行估计， 异方差和自相关会造成有偏估计。引进因变量和解释变量的滞后值， 并采用 Arellano and Bover( 1995) 、 Blundell and Bond( 1998) 的两步系统 GMM 估计法（关键是如何选择合理的工具变量和滞后阶数）。对于银行而言， 宏观变量一般是外生的， 所以选取银行微观因素如风险承担( risk) ， 银行效率( x－eff， t－eff) 作为前定变量或者内生变量; 至于工具变量是否有效，采用 sargan 检验。当工具变量滞后 2 阶时， sargan 检验的 P 值大于 10%（？） ， 因此所选择的所有工具变量是有效的。残差的 1 阶自相关系数显著不为 0， 而2 阶自相关系数无法拒绝为 0， 这个结果表明， 既有充分的依据选择两步 GMM 估计法， 同时消除了自相关。

因变量为风险承担( Z)时，广义货币供应量( M2) 的增长率对银行风险承担的回归系数在 1% 的水平上显著为正， 短期利率( ir) 的系数为负，但不显著；滞后一阶的风险承担( Risk t－1) 的系数显著为正， 说明我国银行风险承担具有连续性和一定的记忆性; 实际GDP 增长率的系数也显著为正；成本效率和利率效率的系数刚好相反， 前者显著为正， 后者显著为负，且成本效率滞后一期的系数也显著为负，符合“差的管理”假说。

在因变量为成本效率和利润效率的方程中， 风险承担的回归系数分别显著为负、 显著为正， 也刚好相反。风险承担对利润效率的回归系数为正， 说明承担的风险越高， 越有利于获得更多的利润， 这符合传统的“高风险高收益” 假说；利润效率对风险承担的回归系数为正， 表明当利润效率提升后， 银行愿意承担更多的风险， 并希望未来获得更高的利润， 这与 Altunbas et al． ( 2007) 的结果一致

货币政策与效率：我国商业银行的利润效率具有顺周期性， 而成本效率是逆周期的。

4、稳健性分析

（1）采用净资产收益率的标准差代替破产风险 Z

（2）不良贷款率( NPL) 作为风险代理变量

个别系数发生变化，所以稳健？

5、结论

( 1) 把总贷款作为产出， 会系统性高估成本效率， 不良贷款对成本效率有着显著的膨胀效应， 而不良贷款作为投入时会低估利润效率; 如果不考虑资本投入， 无论成本效率还是利润效率， 其结果均会高估; 我国商业银行效率的变化与货币政策实践、 宏观经济运行状况基本一致。

( 2) 银行风险承担渠道不仅存在， 而且具有连续性和顺周期性。

( 3) 我国商业银行承担的风险越高， 越有利于获得更多的利润， 符合传统的“高风险高收益” 假说，并且当利润效率提升后， 银行愿意承担更多的风险， 希望未来获得更高的利润。但是， 我国银行效率并非随着风险承担的增加而单调递增， 两者存在倒 U 型关系; 从提升效率的角度来看， 银行应该适度承担风险。

( 4) 成本效率与风险承担的关系， 符合“差的管理” 假说和“成本相抵” 假说。前者认为， 银行较差的管理能力会引起成本效率的下降， 并使风险增加。后者认为， 当银行承担的风险过高时， 银行不得不为可能出现的不良贷款提供更多的准备金， 并为识别信贷风险付出更多的成本， 成本效率随着风险的增加而下降。

( 5)我国商业银行的利润效率具有顺周期性， 而成本效率是逆周期: 当宏观经济下行和货币政策较为宽松时， 利润效率下降， 而成本效率上升。

( 6) 货币政策不仅直接影响银行效率，而且通过风险承担间接影响效率。

（四）风险投资与上市公司全要素生产率关系(赵静梅, 2015)

主要研究的是风险投资对上市公司TFP的贡献，研究方法主要采用了Heckman( 1979) 两阶段方法，第一步研究风投资金能否获取的因素，第二步研究风投对于tfp的贡献，又加入了风投公司的声誉变量来考察（应用情景变换的方法）。我们是否也可以采用两步估计法，计算风险投资对于企业利润效率/成本效率的提升？第一步与本文相同（本文的第一步还有点没看懂，不知道为什么要用两步估计法克服内生性），第二步在原有的sfa模型中加入风险投资作为输入，考察企业业绩提升的效果？

研究主题：

本文选取 2004 － 2012 年我国上市公司数据，研究风险投资与上市公司全要素生产率的关系，结果发现风险投资总体上并没有改善企业的生产效率。

模型设定：

采用全要素生产率( TFP) 衡量企业的生产效率（TFP能动态反映企业应对市场信息变化的能力( Levinsohn and Petrin，2003)），TFP 与企业的技术水平直接相关( Schoar，2002) ）。为了避免生产要素投入可能产生的内生性问题，我们选取 Olley and Pakes( 1996) 的半参数回归方法进行估算。本文以风投声誉为切入口，深入剖析我国风投声誉对企业生产效率的影响机制。

第一，风险投资是否提高了企业的生产效率? 采用 Heckman( 1979) 两阶段方法降低样本选择的内生性问题

第二，风险投资对企业生产效率的经济效应究竟有多大？情景转换回归方法( SＲ，Switching Ｒegression) 进行测试。当高声誉风投机构转换成低声誉的机构时， 企业生产效率显著下降1. 24% ; 当低声誉风投机构转变为高声誉的风投机构时， 企业生产效率显著上升 1. 65% 。

文献综述：

风投机构在投资过程中面临着两大风险: 一是企业的生存风险，二是经理人的道德风险风险投资机构声誉机制对企业的影响主要来自于两个方面: (1) 高声誉风险投资具有丰富的投资经验， 可以为企业物色优秀的管理人员、上市辅导、在并购和战略转型中为企业提供咨询服务。( 2) 高声誉风险投资具有充分的信息渠道和关系网络， 可以为企业的融资、 销售渠道的拓展， 多元化经营等方面提供帮助。具有“认证功能” 和“监督功能”。

Chemmanur et al. ( 2011) 研究风险投资与企业生产效率之间的关系， 他们选取1972 － 2000 年具有风险投资背景的美国制造业样本， 结果发现风险投资显著提高了企业的全要素生产率，并且声誉越高的企业， 对企业生产效率的边际贡献越高。Chemmanur et al. ( 2011) 在估算企业生产效率时，并没有考虑生产要素配置之间的内生性影响， 例如， 当预期企业生产率上升时，企业会增加要素投入; 反之，会减少要素投入，由此导致的内生性问题使得生产效率的估计存在偏误。此外，他们的研究也没有深入分析风险投资声誉对生产效率的机制和经济效应，本文在其基础上选取我国风投样本进行深入拓展。

数据选取与研究设计：

1、样本与数据

2004 － 2012 年间沪深股市所有主板、 中小板和创业板的上市公司作为研究

样本，除去明显缺失和错误的，以及无法用CD函数估计的行业，保留了1004个公司。风险投资背景的数据通过上市公司招股说明书手工搜集， 并与投中集团( China Venture) 公布的数据进行比对增补，采用吴超鹏等( 2012) 对风险投资的定义，将上市公司股东中包含“风险投资”、“创业投资”、“创业资本投资” 等界定为风投机构。

2、TFP

根据 Olley and Pakes( 1996) 的基本思路，同时借鉴 Loecker( 2007) 将企业出口行为引入到 OP 框架的具体做法，按照鲁晓东和连玉君( 2012) 的研究设计估算全要素生产率。

3、风险投资声誉

分别采用前3年风险投资机构投资的额度(市场份额) 、前3年风险投资参股企业上市后的总资产规模(市场份额)四个指标衡量，考虑到数据的平滑性， 本文采用 3 年期的滚动窗口加总得到。根据 Tian( 2012) 联合投资声誉指标的处理， 本文以风投机构声誉的平均值作为联合投资公司的声誉指标， 并分别采用最大值和中位数进行稳健性测试。

4、风险投资影响生产效率的计量模型

尽可能的降低样本选择和内生性问题，本文选择 Heckman( 1979) 两阶段方法研究：

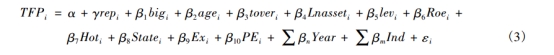
实证结果与分析：

1、变量描述性统计

2、Heckman（1979）两阶段分析

投行声誉提高了风险投资参股的概率，认证功能明显；发行市盈率越高，风投机构投资概率越大，出口的企业比非参与出口企业的概率明显高；大规模的企业能产生规模效应，且更能满足上市的基本条件；

表明在控制了风险投资的选择后， 高声誉风险投资显著提高了企业的生产效率。

为了更清晰的显示风投声誉对 TFP 的影响， 本文分别将 4 种声誉变量加入模型( 3)回归，风投声誉的 4 个指标均与 TFP 显著正相关。

3、内生与稳健性

尽管 Heckman( 1979) 可以在一定程度上降低样本的自选择问题， 然而 Francis et al.( 2011) 指出该方法的结果非常不稳定， Lawrence et al. ( 2011) 建议采用倾向值配对方法( PSM) ，通过构建配对组合来控制自选择和内生性对模型的负面影响。PSM 的结果与前文几乎一致，由于文章篇幅限制，文中并未报告

风险投资的经济效应：情景转化测试

转换回归的思想是， 对于风投背景的企业， 如果没有风险投资的情景下，TFP 如何变化; 反之， 对于非风投背景的企业， 如果有风险投资时TFP 如何变化。

整体来看，有无风险投资对企业的生产效率并无明显的差异， 风险投资并没有显著提高企业的生产效率；高声誉的风投机构可以有效改善企业生产效率。

（五）替代方法（Koutsomanoli Filippaki and Mamatzakis(2010)）

上述模型的估计方法都较为复杂。作为一个替代方法，可以借鉴 Koutsomanoli Filippaki and Mamatzakis(2010)文中使用的两步估计法：第一步采用传统的 SFA 模型估计出 TE 值，第二步则以 TE 为被解释变量，采用 Arellano and Bond(1991)或 Arellano and Bover(1995)提出的动态面板模型估计调整速度

是否需要掌握推导过程及其中原理？还是直接用就好？（STATA命令是否有现成的？）

1、Koutsomanoli Filippaki and Mamatzakis(2010)两步估计法

INTRODUCTION

In detail, we opt for the stochastic frontier analysis within a translog cost function framework, so as to derive bank-specific inefficiency scores, while as a second step we apply a multi-period forward-looking rational expectations specification to measure the speed of adjustment to the optimal cost level. Using a dynamic panel model we opt for a quadratic loss function to account for adjustment costs between the current level of inefficiency and the optimal one. To this end, the adjustment of banks' costs is seen as a dynamic process based on rational expectations, and not as a static procedure. This idea first came up in the literature of aggregate demand.

THEORETICAL SPECIFICATION

1）SFA (Aigner et al. (1977), Meeusen and Van den Broeck (1977) ) to estimate cost efficiency (设定与一般的sfa模型相同)

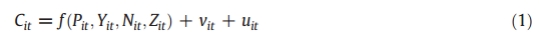
Cit observed total cost for bank i at year t

P : a vector of input prices

Y : a vector of outputs of the firm,

Ν : a vector of fixed netputs (quasi-fixed quantities of either inputs or outputs that affect variable cost)

Z stands for a set of control variables.

vi, corresponds to the random fluctuations and is assumed to follow a symmetric normal distribution around the frontier

ui, accounts for the firm's inefficiency and is assumed to follow an exponential distribution

2）cost efficiency function: translog specification

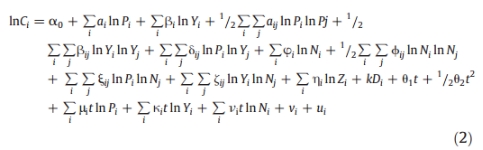
The cost frontier can be approximated by maximum likelihood, and efficiency levels are estimated using the regression error, ε=vi+ui.

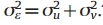 measure a firm’s inefficiency.

normal-exponential model: ,,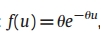   

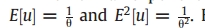
Firm level inefficiency: ]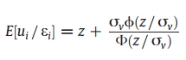

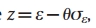·Next step

the dynamics of inefficiency scores derived from the first stage are modelled using a forward-looking rational expectations specification

According to this approach the typical bank is assumed to minimize the conditional expectation of a discounted quadratic loss function (L). This objective function takes the form

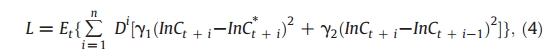
where Et is the conditional expectations operator on the information set at time t, Di denotes a discount factor less than unity, and γi (i=1,2) are the non-negative adjustment cost coefficients. γ1 represents the disequilibrium parameter, measuring the deviation of actual costs InCt + i at time t+i from its optimal (long-run equilibrium) value InCt⁎ + i

γ2 counts for the short-run adjustment (transaction) between any two consecutive periods

式（4）对Ct+1求偏导，得到：

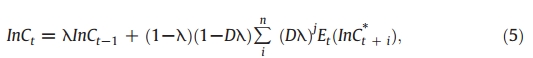
其中λ is the stable root of the Euler equation。并假设lnC符合简单随机过程。

简化的成本函数如下：

To this end, Eq. (7) within the context of the present analysis reflects a general dynamic panel data model. λ captures the persistence of inefficiency scores over time, whilst 1−λ reflects the adjustment speed to equilibrium.

As part of a sensitivity analysis, we also estimate the above dynamic panel data model by including to the cost adjustment equation some exogenous explanatory variables that are related to the management of banks.

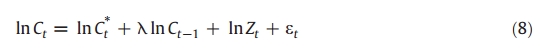
The lagged dependent variable may be correlated withεt. If this is the case neither the fixed effects estimators nor the random effects generalized least squares estimators are unbiased in a dynamic panel data model.

To this end, in this paper we estimate the dynamic panel data model using the generalized Method of Moments procedure proposed by Arellano and Bover (1995).

DATA

Bank inputs and outputs definition follows Sealey and Lindley (1977): banks as institutions that collect deposits, using labour and physical capital, to transform them into loans and other earning assets.

input prices:

the price of labour is proxied by the ratio of personnel expenses to total assets

the price of deposits is defined as the ratio of interest expenses to total funds

The output vector

loans (defined as total loans net of provisions)

other earning assets,

Total cost is defined as the sum of overheads (personnel and administrative expenses), interest, fee, and commission expenses.

Fixed Netput: physical capital and equity(risk factor)

Country-level variables

EMPIRICAL RESULTS

先算了各国银行的成本效率，及无效率程度

Despite the observed heterogeneity in the reported inefficiency levels, an efficiency analysis fails to identify differences in the speed of reaction to a shock in the short term. As a way of tackling this issue, we employ the quadratic loss function that could provide evidence on convergence, if any, in the speed of adjustment towards long-run equilibrium. If Europe's banking markets have become more alike over the eight-year period under consideration, we would expect to observe convergence in the speed of adjustment across countries.

2、Arellano and Bover(1995)估计TE调整速度

Next, we employ the GMMestimator for dynamic panel data models proposed by rellano and Bover (1995) so as to estimate Eq. (7), which includes the lagged dependent variable (Cit−1) as an endogenous explanatory variable. Based on Arellano and Bover (1995), we take first difference of Eq. (7) on both sides and remove in this way the firm specific effects. The lagged dependent variables with two or more periods are likely to be valid instruments for the equation in the first differences, depending on whether disturbance εit is serially correlated.

解释：Unrestricted model：In effect, λ identifies the persistence to a given level of inefficiency, whereas 1−λ captures the adjustment speed to the long-run equilibrium. λ takes values from 0 to 1, whereas the longer the current suboptimal inefficiency level persists, the higher the value of λ.

For comparison purposes, we also estimate a restricted model by imposing the single adjustment speed restriction, i.e., letting λc=λ for all countries.但由于在无限制模型中估出来的大多数国家的λ是显著的，所以这个结果要谨慎对待。

之后研究了adjustment speed λ是否有变化：

we split our sample into two sub-periods 1998–2001 and 2002–2005.

Sensitivity Analysis

employ the GMM estimator to estimate a dynamic panel data model by including to the cost adjustment equation some exogenous explanatory variables that are related to the management of banks (ROA, RO loan loss provisions, net interest margin ratio)

鉴于某些国家样本较少，只估算一个common persistent parameter，来判断各系数是否有改变。

Arellano, M., O. Bover, 1995, Another look at the instrumental variable estimation of errorcomponents models, Journal of Econometrics, 68 (1): 29-51

Koutsomanoli-Filippaki, A., E. C. Mamatzakis, 2010, Estimating the speed of adjustment of european
banking   全套毕业设计论文现成成品资料请咨询微信号：biyezuopin QQ：2922748026     返回首页 如转载请注明来源于www.biyezuopin.vip