平板单元（Mindlin板）的热-结构耦合计算

如图所示的平板，其中一边固支，并且受到太阳光的照射，其中太阳的热流密度矢量如图所示：

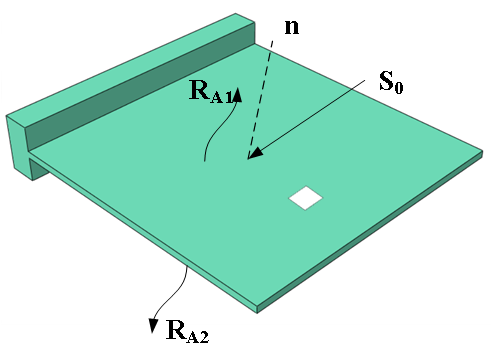
从平板上取单元，如图所示，并取其中的微元，其受热和热流密度如图所示，包括：x、y和z三个方向的热流，A1面受到太阳照射的热流输入、A1和A2面辐射散热产生热流输出。

其三维热传导单元的热平衡方程：

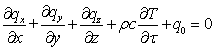
热流密度与温度的关系：

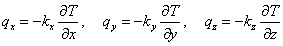
带入热平衡方程，由于结构材料本身不发热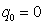，，得到最终的热平衡方程：

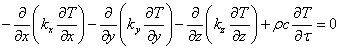
边界条件（z方向的热流变化等于太阳光的照射产生的热流输入和辐射散热之差）：

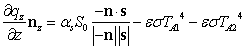
采用三维八节点的Lagrange插值形函数，对平板单元热学方程进行有限元离散，单元的温度场用形函数和节点温度表示为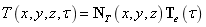： ，并使用Garlerkin法在单元内对热平衡方程进行积分：

得到最终的热平衡方程：

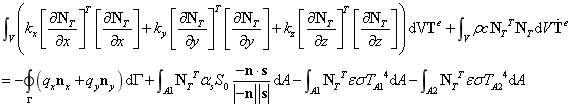
单元方程写为：

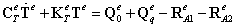
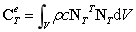
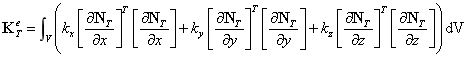
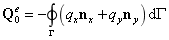
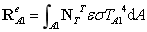
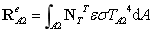
组合成整体方程：

 ，     

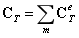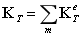
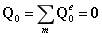
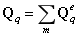
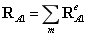
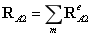
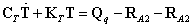
时间差分法和牛顿内迭代法求解时间域内温度响应：

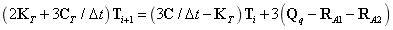
结构的有限元方程（使用Mindlin板理论，更具有普遍性，可以利用等参元表示任意四边形单元）：

使用等参变换：

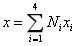
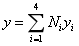
其中差值函数：

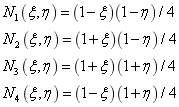
对位移进行同样的差值：

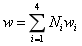
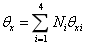
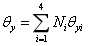
使用矩阵形式表示为：

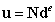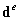（其中为单元节点的位移向量）

其中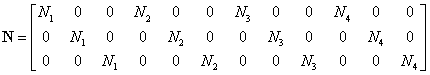

Mindlin板考虑了横向剪切变形，其应变向量为：

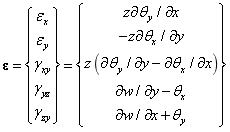
将上式中的位移用节点的插值表示，并进行微分得到：

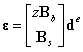
其中

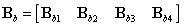
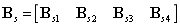
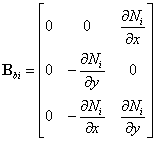
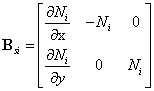
应力：

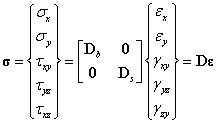
其中：

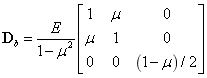
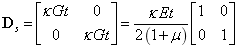
其中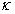为剪切修正因子，对各向同性材料，取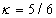

（上面黄色部分事实证明不可，进行重新推导）

使用Mindlin板理论对结构进行有限元离散。

对于二维的四边形单元，在只考虑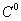连续的情况下，使用如下的等参变化进行插值表示：

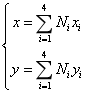
其中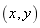表示任意点的坐标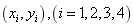，表达四边形单元的节点坐标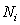，表示拉格朗日插值形函数，其表达式如下：

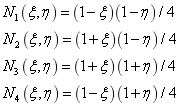
Mindlin板单元为广义的平板单元，考虑其位移和转动是各自独立的场函数，对其进行独立的插值表示：

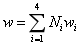
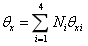
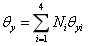
使用矩阵形式表示为：

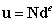
其中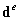为单元节点的位移向量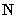，为形函数矩阵：

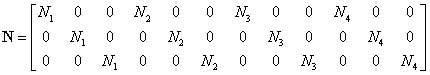
Mindlin板理论考虑了横向剪切变形，

单元的刚度矩阵：

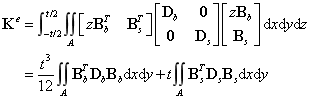
错误

单元刚度矩阵修改为：

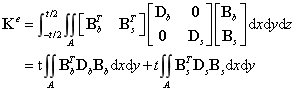
单元的质量矩阵：[参考文献：考虑剪切影响的Mindlin板单元质量阵]

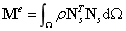
其中为单元积分区域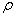；为材料的质量密度矩阵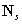，表示质量矩阵插值形函数矩阵，表达式如下所示：

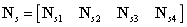
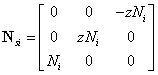
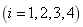
将单元刚度矩阵和单元质量矩阵组装成总体刚度矩阵和总体质量矩阵：

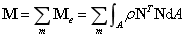
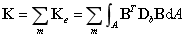
其中阻尼矩阵用比例阻尼表示：

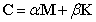
得到结构的最终有限元方程：

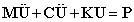
递推公式：

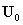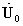1. 确定初始位移、速度和加速度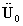，给定时间步长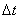和参数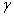、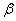，计算积分常数
；；；；
；；；

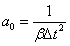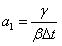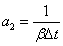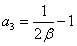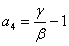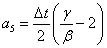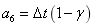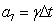
2. 计算等效刚度矩阵：

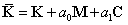
3. 计算ti+1时刻的等效载荷：

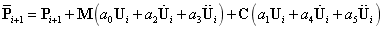
4. 计算ti+1时刻的位移、速度和加速度：

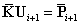
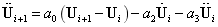
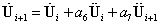
5. 重复2到4步骤，记录每一步的动力响应值，直到算完给定的时间步nt

结构热载荷计算

由于物体的热膨胀只产生线性应变，剪切应变为0，平板单元由于温度变化产生的应变表达式为：

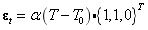
其中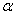是材料的线膨胀系数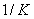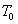（），是初始温度场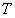，是结构的瞬态温度场。

热载荷计算

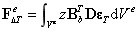
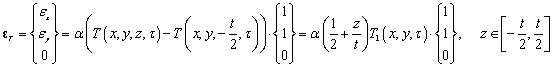
重新推导

对于薄板，不计厚度方向应力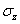引起的变形，根据广义胡克定律，其物理方程为：

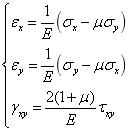
其中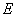，为材料的弹性模量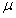；为泊松比。

由上式可以求出应力分量：

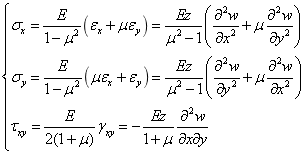
将板单元界面上的各点的应力对板的中面取力矩，再将其对板的厚度积分，可以得到弯矩、剪力的表达式如下所示：

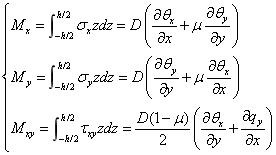
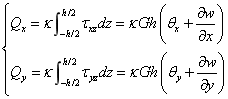
上式中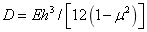表示板的弯曲刚度（抗弯刚度），

热载荷推导

应变能密度：

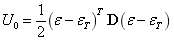
单元的应变能：

对应变和应力的处理（论文里扩充）

应变和应力计算的方法：

1、单元平均或节点平均（常用于处理三角形单元，应力在单元内是常数，取绕节点各个单元的应力的平均值或者面积加权平均。）；

2、总体应力磨平（工作量十分庞大，相当于进行了两次有限元计算，一次位移场计算，一次应力场计算）；

3、单元应力磨平（可以利用精度较高的高斯积分点的应力值来改进等参元节点应力的近似性）；使用应力外推的方法获得每个单元在每个节点处的应力，然后对于每一个节点，将其周围每一个单元算得的应力值作平均处理，获得节点处最终的应力值。

4、分片应力磨平。

对于本方法，最终采用单元应力磨平的方法进行计算法