eograph;">在图7(b)中,为更充分说明问题,基于公式(32),再随机取一组试验样本超参数值 ,针对前8阶固有频率估计出其多维核密度概率分布函数后,再对其进行极大似然估计,得到的估计参数结果为
,针对前8阶固有频率估计出其多维核密度概率分布函数后,再对其进行极大似然估计,得到的估计参数结果为 ,与原超参数值
,与原超参数值 略有差异,这是因为模型样本的数量不可能取为无限大,试验样本参数的估计精度显然受限于模型样本的数量,但似然函数的峰值仍可在参数
略有差异,这是因为模型样本的数量不可能取为无限大,试验样本参数的估计精度显然受限于模型样本的数量,但似然函数的峰值仍可在参数 附近即
附近即 取得。
取得。


(a) (b)
(b) 
图7 仅考虑弹性模量为随机场变量时前8阶结构固有频率构成的8维分布密度函数估计的
当同时考虑弹性模量 随机场和质量密度
随机场和质量密度 随机场时,试验样本的输入参数分别取为两组:
随机场时,试验样本的输入参数分别取为两组: ,
, ;
; 和
和 。固定两个随机场的相关长度即
。固定两个随机场的相关长度即
 ,分别针对两组参数采用上述过程来估计似然函数
,分别针对两组参数采用上述过程来估计似然函数 取得极大值时随机场对应超参数均方差
取得极大值时随机场对应超参数均方差 和
和 。由图8可见:针对结构的8阶固有频率进行极大似然估计后得到取得最大值处的超参数与输入参数相同。
。由图8可见:针对结构的8阶固有频率进行极大似然估计后得到取得最大值处的超参数与输入参数相同。


(c)  (d)
(d) 
图8  和
和 同时为随机场时前8阶结构固有频率的8维核密度分布函数的对数似然函数值
同时为随机场时前8阶结构固有频率的8维核密度分布函数的对数似然函数值
4.2 板算例验证
图9所示一端固定的正方形钢板,厚度为0.01m,质量密度均值为 ,弹性模量
,弹性模量 的均值为210GPa,将板划分为
的均值为210GPa,将板划分为 的矩形板单元。
的矩形板单元。


图 9板的三维模型(left)和有限元模型(right)
设钢板弹性模量 为二维高斯随机场,基于式(1)对其进行二维K-L展开,
为二维高斯随机场,基于式(1)对其进行二维K-L展开, 的均值为
的均值为 ,则
,则 可离散化为
可离散化为

 (36)
(36)
取弹性模量随机场 的超参数
的超参数 作为试验样本和模型样本的输入参数。将板划分为
作为试验样本和模型样本的输入参数。将板划分为 个单元,得到
个单元,得到 随机场在板内的分布图10(a)和10(b);将其划分为
随机场在板内的分布图10(a)和10(b);将其划分为 个单元时,得到
个单元时,得到 在板内的随机分布图为图10(c)和10(d)。由图10可见:E的均值在
在板内的随机分布图为图10(c)和10(d)。由图10可见:E的均值在 附近,并且在x和y方向均呈随机分布。
附近,并且在x和y方向均呈随机分布。


(a) (b)


(c) (d)
图10 板的杨氏模量随机场分布
当仅考虑质量密度 为随机场时,将其进行二维K-L展开后见式(37),其均值为
为随机场时,将其进行二维K-L展开后见式(37),其均值为 ,取其超参数
,取其超参数 时,图11显示了随机场
时,图11显示了随机场 在钢板内的分布,其中图11(a)和11(b)为将板划分为225个单元时
在钢板内的分布,其中图11(a)和11(b)为将板划分为225个单元时 的分布图,而图11(c)和图11(d)中板的划分网格数为400.
的分布图,而图11(c)和图11(d)中板的划分网格数为400.

 (37)
(37)


(a) (b)


(c) (d)
图11 板的质量密度随机场分布
仅考虑弹性模量随机场时,取一组超参数 ,具体参数取值为
,具体参数取值为 ,
, ,
, ,针对每一个超参数
,针对每一个超参数 均取100块板的前六阶固有频率组成模型矩阵样本
均取100块板的前六阶固有频率组成模型矩阵样本
 ,总计采用
,总计采用 块板,共计1000个模型矩阵样本
块板,共计1000个模型矩阵样本 。下面将基于该模型数据样本对试验数据样本进行核密度估计和极大似然估计。
。下面将基于该模型数据样本对试验数据样本进行核密度估计和极大似然估计。
为验证板的随机场模型,分别取超参数 、
、 、
、 和
和 进行数值模拟,每个超参数取500块板的前六阶固有频率矩阵分别组成试验数据样本
进行数值模拟,每个超参数取500块板的前六阶固有频率矩阵分别组成试验数据样本 、
、 、
、 和
和 ,再采用式(32)计算
,再采用式(32)计算 的对数似然函数值
的对数似然函数值 。结果列在表1中。
。结果列在表1中。
从表4-1可以看出,根据 取得极大值的点,板的二维随机场模型可以很好地估计出试验样本的超参数
取得极大值的点,板的二维随机场模型可以很好地估计出试验样本的超参数 ,与试验样本的输入参数
,与试验样本的输入参数 、
、 、
、 和
和 基本能一致,从而说明所建模型是可靠的。与工字梁的一维随机场模型一样,模型样本组数不可能无限大,试验样本参数的估计精度受限于模型样本数量,采用极大似然估计方法去估计参数为
基本能一致,从而说明所建模型是可靠的。与工字梁的一维随机场模型一样,模型样本组数不可能无限大,试验样本参数的估计精度受限于模型样本数量,采用极大似然估计方法去估计参数为 的试验样本时,仍能估计到试验样本输入参数附近。
的试验样本时,仍能估计到试验样本输入参数附近。
表1 考虑弹性模量随机场时钢板试验样本的极大似然估计
|
试验样本输入参数

|
对数似然函数极大值

|
极大值点对应的超参数
|
基于试验样本获得的固有频率( ) )
|
|

|

|

|

|
|

|

|

|

|

|

|
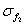
|

|

|
|
(5,500,500)
|
10344.12
|
5
|
500
|
500
|
8.6185
|
0.0581
|
13.5240
|
0.0877
|
51.6952
|
0.3545
|
|
(6,300,700)
|
9190.03
|
6
|
300
|
700
|
8.6159
|
0.0659
|
13.5199
|
0.0969
|
51.6793
|
0.3957
|
|
(2,100,700)
|
13712.95
|
2
|
100
|
700
|
8.6197
|
0.0131
|
13.5254
|
0.0183
|
51.7022
|
0.0776
|
|
(9,430,650)
|
8151.44
|
9
|
400
|
700
|
8.6204
|
0.1083
|
13.5271
|
0.1627
|
51.7069
|
0.6553
|
表中 和
和 分别表示变量的均值和均方差。
分别表示变量的均值和均方差。
进一步,取弹性模量随机场 的超参数
的超参数 ,取质量密度随机场
,取质量密度随机场 的超参数为
的超参数为 。当
。当 分别取为(1GPa,2GPa,…,10GPa)且取试验样本超参数
分别取为(1GPa,2GPa,…,10GPa)且取试验样本超参数 、
、 时,可获得样本第二阶固有频率
时,可获得样本第二阶固有频率 的二维核密度分布函数估计,如图12(a)所示;当取
的二维核密度分布函数估计,如图12(a)所示;当取 的随机场超参数
的随机场超参数 ,取
,取 的随机场超参数
的随机场超参数 ,分别取
,分别取 为(50kg/m3,100kg/m3,…,500kg/m3)且取试验样本超参数为
为(50kg/m3,100kg/m3,…,500kg/m3)且取试验样本超参数为 、
、 ,可得
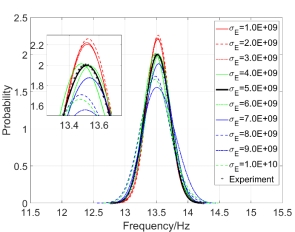
,可得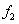 的二维核密度分布函数估计图12(b)。图12再次显示:质量密度随机场比弹性模量随机场对结构固有频率核密度分布函数的影响更大。
的二维核密度分布函数估计图12(b)。图12再次显示:质量密度随机场比弹性模量随机场对结构固有频率核密度分布函数的影响更大。

(a) (b)
图12 同时考虑弹性模量和质量密度为随机场变量时第二阶固有频率的二维核密度估计
此外,固定超参数 中的
中的 ,以相关长度
,以相关长度 和
和 作为变量,板固有频率似然函数的变化如图13(a)和(b)所示,可见二维情况下,网格划分对于似然函数中超参数估计的精度影响不大,且划分网格过密,导致计算时间增加很多(400网格(b)的计算时间近20小时,图(a)划分为225网格所需计算时间仅为7小时);故在图13(c)和图13(d)中计算超参数极大似然估计值的分布时,将板划分为
作为变量,板固有频率似然函数的变化如图13(a)和(b)所示,可见二维情况下,网格划分对于似然函数中超参数估计的精度影响不大,且划分网格过密,导致计算时间增加很多(400网格(b)的计算时间近20小时,图(a)划分为225网格所需计算时间仅为7小时);故在图13(c)和图13(d)中计算超参数极大似然估计值的分布时,将板划分为 个单元,其中试验样本超参数分别取为
个单元,其中试验样本超参数分别取为 和
和 。
。
由图13(c)和(d)可见:根据试验样本基于结构前六阶固有频率进行似然估计时, 取得极大值时对应的超参数
取得极大值时对应的超参数 分别为
分别为 和
和 ;基于多维核密度估计,采用极大似然估计均能准确估计出似然函数取极大值时的试验样本超参数,且估计出的超参数与试验样本的输入参数非常接近,从而验证了所建模型有效性。
;基于多维核密度估计,采用极大似然估计均能准确估计出似然函数取极大值时的试验样本超参数,且估计出的超参数与试验样本的输入参数非常接近,从而验证了所建模型有效性。


(a) 225elements,  (b) 400elements,
(b) 400elements, 


(c)  (d)
(d) 
图13 仅考虑弹性模量为随机场变量时板的固有频率对数似然函数值图
类似地,仅考虑质量密度为随机场,其试验样本输入超参数分别为 和
和 时,图14为基于板的前六阶固有频率获得的对数似然函数值分布图。
时,图14为基于板的前六阶固有频率获得的对数似然函数值分布图。


(a)  (b)
(b) 
图14 仅考虑质量密度为随机场变量时板的固有频率对数似然函数值图
图15为仅考虑弹性模量为随机场变量且其K-L展开后的超参数为 时,钢板前六阶随机固有振型的分布图。
时,钢板前六阶随机固有振型的分布图。


(a)第一阶固有振型 (b)第二阶固有振型


(c)第三阶固有振型 (d)第四阶固有振型


(e)第五阶固有振型 (f)第六阶固有振型
图15 仅考虑弹性模量随机场时钢板的随机固有振型分布图
同时考虑 和
和 为随机场,且其超参数分别取为
为随机场,且其超参数分别取为 和
和  ,板的前六阶随机固有振型见图16所示。
,板的前六阶随机固有振型见图16所示。


(a)第一阶主振型 (b) 第二阶主振型


(c)第三阶主振型 (d) 第四阶主振型


(e)第五阶主振型 (f) 第六阶主振型
图16 考虑弹性模量和质量密度同为随机场时钢板的前六阶随机固有振型分布图
|
|

|

|

|

|

|

|

|

|
|
 为随机场 为随机场
|
6500.32
|
1634.32
|
404.02
|
296.12
|
10101.01
|
280.73
|
157.55
|
145.99
|
|
 和 和 同为随机场 同为随机场
|
6514.18
|
1635.93
|
404.93
|
297.85
|
655.26
|
208.69
|
162.51
|
141.96
|
5 结论
提出的基于随机场理论的超参数模型能够表征结构的不确定性,反映结构参数的不确定性与空间关联性,可以描述实际结构参数的随机变化特性。算例表明,模型超参数可以通过结构的输出响应即结构固有频率进行量化,得到结构超参数的标准差和自相关距离,具有一定的应用性。提出的方法也适用于其他参数,也可以对其他材料参数或结构参数建立随机场超参数模型并进行量化。
参考文献
[1] 王春水,李大磊,张二亮.基于随机场理论的结构不确定性表征与量化[J].制造业自动化,2015,(第15期).
[2] 白长青,张红艳.不确定性转子系统的随机有限元建模及响应分析[J].动力学与控制学报,2012,(第3期).
[3] FENG X, LU Z X, YANG Z Y, et al. Analysis on the variances of material and structural properties based on random field theory[J]. Probabilistic Engineering Mechanics.2011(26):222-230.
[4] BETZ W, PAPAIOANNOU I, STRAUD D. Numerical methods for the discretization of random fields by means of the Karhunen–Loève expansion[J].Computer Methods Applied Mechanics and Engineering.2014(271):109-129.
[5] Roger G. Ghanem, Pol D. Spanos. Stochastic finite elements:a spectral approach[M]. Dover Publications, 2003
[6] 季文美等著. 机械振动. 科学技术出版社, 1985.06.
[7] 胡于进,王璋奇.有限元分析及运用[M].清华大学出版社,2009
[8] SOIZE C. A computational inverse method for identification of non-Gaussian random fields using the Bayesian approach in very high dimension[J].Computer Methods Applied Mechanics and Engineering,2011(07).
, 带有随机场变量结构的动力特性分析
摘要:考虑结构参数的随机不确定性和空间关联性,提出一种基于随机场理论的超参数模型来表征参数的随机不确定性,并基于超参数模型分析了不同类型结构的随机动力特性。首先,采用高斯随机场理论来描述结构材料参数的不确定性,将不确定参数表征为随机场的标准差和相关性长度后,进而利用Karhunen-Loeve展开法对随机场参数进行离散化;基于离散化后的随机参数和有限元法,构建结构的动力特性分析模型;利用多维核密度估计法构建出结构随机固有频率的概率分布密度函数,并采用极大似然估计法量化结构的随机场参数,从而验证所提方法的有效性和模型的适用性。
关键字:随机场参数;Karhunen-Loeve展开;极大似然估计;多维核密度估计;随机动力特性
1 引言
实际结构材料属性的复杂性以及生产制造过程中的各种随机误差等因素都会造成结构参数的不确定性,如机床的振动,加工过程中温度的随机变化等,会使得相同材料、相同加工方法制造出的名义尺寸相同的一组结构件之间存在不确定性,最终导致结构材料参数不仅在其均值附近呈现随机波动性,且其波动与加工尺寸方向呈现出一定的关联性。此外,一组名义尺寸相同的结构件,因其材料参数具有的不确定性,因而导致其动力学特性虽然相似但不尽相同,因此亟需构建出有效模型来表征结构参数的不确定性。
王春水等[1]运用一维高斯随机场模型,并运用K-L展开将随机场离散到有限元模型,分析了悬臂梁的动力特性;白长青等[2]用一维随机场函数表示轴的弹性模量、剪切模量、密度等参数,研究了不确定性转子系统的随机有限元建模及动力响应分析;Feng X等[3]运用基于随机场理论的随机有限元法研究结构材料力学性能的变化规律,利用一维随机场对梁的弹性模量、载荷和质量密度进行表征,研究了简支梁的动力学特性。
目前,关于结构不确定性的表征及参数修正的研究主要集中在对某些结构或材料参数,如弹性模量、惯性矩、厚度等参数展开,如将其作为离散随机变量,考虑其均值及方差后输入结构系统进行不确定性分析,所构建的模型本身复杂度不高,虽可采用各种有效方法进行随机有限元分析,但本质上并不能精确反映实际结构的真实不确定情况。事实上,影响结构材料参数不确定性的因素有很多,导致材料参数在结构空间上呈现随机分布,如轧制钢板时,轧制头的跳动呈现三角函数规律,必然导致结构厚度的薄厚不匀,相应地导致结构的杨氏模量和质量密度的随机性与结构空间尺寸密切相关。为了研究关键参数的随机性,对结构尺寸和材料的关键参数引入随机场模型,用来描述结构材料参数的空间相关性是非常必要的。
本文针对结构材料参数的不确定性,提出了一种基于随机场理论的结构动力特性分析方法。首先,采用随机场理论的超参数模型表征结构材料参数的不确定性,基于高斯核函数的随机场模型对不确定性随机场结构参数进行量化后,再采用Karhunen-Loeve展开方法对随机场超参数模型进行了模拟和离散,基于有限元法对结构动力特性进行了分析,并基于多维核密度估计获得了结构固有频率的概率分布密度函数;将试验和模拟结果进行对比后,采用最大似然估计法对模型参数进行了量化。最后,通过简支梁和板两个算例从一维和二维角度验证了所提出的材料参数随机场模型的适用性和有效性。
2 不确定性的随机场表征
机械加工、热处理及材料自身的不确定性等误差都会导致结构的不确定性,这些误差一般都很小且相互独立(CM一个评审人意见),根据中心极限定理:相互独立的大量微小随机变量,其分布服从高斯分布,高斯分布假设便于计算且可使问题获得求解。本文拟采用高斯随机场模型来描述结构弹性模量的不确定性。(也可参考随机场PDF及参考文献,为什么要考虑用高斯随机场,而不是其他随机场)
2.1 高斯随机场模型
高斯随机场具有两个特点:1)其数学期望 和方差
和方差 为与位置坐标无关的常数,即
为与位置坐标无关的常数,即 ,
, ,其中
,其中 为随机数,
为随机数, 表示空间一点;2)其自协方差函数只与随机场上两点的相对位置距离有关,而与两点的绝对位置坐标无关,即自协方差为
表示空间一点;2)其自协方差函数只与随机场上两点的相对位置距离有关,而与两点的绝对位置坐标无关,即自协方差为 ,
, 为两点之间的相对距离,
为两点之间的相对距离, 为随机场的自相关函数;此外,相关距离
为随机场的自相关函数;此外,相关距离 为高斯随机场的另一个重要参数,表示在相关距离
为高斯随机场的另一个重要参数,表示在相关距离 内的参数具有明显的关联性。可见:建立随机场的关键是构建其协方差矩阵。
内的参数具有明显的关联性。可见:建立随机场的关键是构建其协方差矩阵。
有限元框架下,计算结构的动力特性需要将连续的高斯随机场离散化为随机变量向量。高斯随机场常用的离散方法有:谱表示法、Karhunen-Loeve展开法(简称K-L展开法)等。本文将采用K-L展开法对结构随机场参数进行离散化。
2.2 Karhunen-Loeve展开
Karhunen-Loeve展开已在连续过程中得到了广泛运用,其展开实质是将随机场分解为一系列不相关的随机变量和确定系数(如特征函数和特征值)。K-L展开具有如下优点:对任意类型随机场都有均方收敛的特点;相较于其他方法,当展开的有限项相同时,具有最小的均方误差 [原文献6]。在K-L展开式中,随机场 可展开为一组可数的正交随机变量,即可展开成随机标量
可展开为一组可数的正交随机变量,即可展开成随机标量 的组合。具体展开过程如下[1]:
的组合。具体展开过程如下[1]:
 (1)
(1)
式中 为空间一点坐标,
为空间一点坐标, 为随机场数学期望,
为随机场数学期望, 为随机事件,
为随机事件, 为零均值互不相关的高斯随机序列,
为零均值互不相关的高斯随机序列, 和
和 分别为随机场自协方差矩阵
分别为随机场自协方差矩阵 的特征值和特征函数。
的特征值和特征函数。
随机场K-L展开的关键是获得自协方差矩阵 的特征值和特征函数,由于所研究的随机场的协方差矩阵是定义在规则的几何空间域上,其表达式易知,故可较容易地得到其特征值和特征向量,从而实现随机场参数的K-L展开。自协方差矩阵
的特征值和特征函数,由于所研究的随机场的协方差矩阵是定义在规则的几何空间域上,其表达式易知,故可较容易地得到其特征值和特征向量,从而实现随机场参数的K-L展开。自协方差矩阵 的具体求解过程如下[5]。
的具体求解过程如下[5]。
 (2)
(2)
其中自协方差函数 为有界、对称和正定,如此可保证特征值和特征函数有如下性质:1) 特征函数的集合
为有界、对称和正定,如此可保证特征值和特征函数有如下性质:1) 特征函数的集合 是正交完备的;2) 对每个特征值
是正交完备的;2) 对每个特征值 ,最多对应有限多个线性无关的特征函数;3) 最多仅有一个可数的无穷大特征值集合;4) 特征值都是正实数;5) 自协方差矩阵
,最多对应有限多个线性无关的特征函数;3) 最多仅有一个可数的无穷大特征值集合;4) 特征值都是正实数;5) 自协方差矩阵 可分解为如下形式:
可分解为如下形式:
 (3)
(3)
在一维随机场情况下,为求解方程中的特征函数 ,可取如下的自相关核函数
,可取如下的自相关核函数
 (4)
(4)
其中L为随机场的相关长度,反映两个点 和
和 之间相关性的衰减程度。因此
之间相关性的衰减程度。因此 为变量
为变量 和参数L的函数;且一维随机场下,(2)式的积分区域
和参数L的函数;且一维随机场下,(2)式的积分区域 为实数区间,可取为
为实数区间,可取为 。因此,式(2)可转换为:
。因此,式(2)可转换为:
 (5)
(5)
式进一步展开得到:
 (6)
(6)
方程对 求一阶导可得
求一阶导可得
 (7)
(7)
方程再次对 求导并将
求导并将 用
用 代替后可得一般形式下的微分方程为
代替后可得一般形式下的微分方程为
 (8)
(8)
令 ,方程可转变为
,方程可转变为
 (9)
(9)
为求解微分方程(9),需获知其边界条件。不妨将 和
和 分别代入式(6)和(7)整理得到如下边界条件:
分别代入式(6)和(7)整理得到如下边界条件:
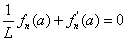 (10)
(10)
 (11)
(11)
综上,式转换成了一般形式的微分方程及其边界条件和,可知其通解为:
 (12)
(12)
将方程代入边界条件和,化简整理得
 (13)
(13)
基于式(13),欲使微分方程(9)的解即式(12)存在,须满足如下条件:
 (14)
(14)
求解式,用 表示第一个方程的解,其解在区间
表示第一个方程的解,其解在区间 内,用
内,用 表示第二个方程的解,其解位于区间
表示第二个方程的解,其解位于区间 内,其中
内,其中 表示式(1)K-L展开式所取的截断个数且
表示式(1)K-L展开式所取的截断个数且 为偶数,可得到对应于
为偶数,可得到对应于 为奇数和
为奇数和 为偶数的特征函数分别为:
为偶数的特征函数分别为:
 (15)
(15)
 (16)
(16)
进一步,根据转换关系 求得
求得 为奇数和
为奇数和 为偶数时对应的特征值分别为:
为偶数时对应的特征值分别为:
 (17)
(17)
 (18)
(18)
基于方程(14)-(16),当给定条件:设梁长1米,则 ,相关长度
,相关长度 ,取截断个数为
,取截断个数为 时,可获得特征函数
时,可获得特征函数 的图像如图1中左图所示。由图直观可见:特征函数实为一系列三角函数,其周期和幅值大小均与其阶数
的图像如图1中左图所示。由图直观可见:特征函数实为一系列三角函数,其周期和幅值大小均与其阶数 的取值有关,即
的取值有关,即 越大,
越大, 的周期越小。基于方程(17)-(18),取梁长1米,
的周期越小。基于方程(17)-(18),取梁长1米, ,取相关长度
,取相关长度 ,可得到特征值如图1(b)所示。由图1可见:在基于方程(1)由特征值
,可得到特征值如图1(b)所示。由图1可见:在基于方程(1)由特征值 和特征函数
和特征函数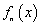 组合成随机场
组合成随机场 时,右图中所取的相关长度
时,右图中所取的相关长度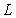 值越大,低阶特征值如
值越大,低阶特征值如 的取值越大,则对应于左图中的低阶特征函数即
的取值越大,则对应于左图中的低阶特征函数即 在
在 中的占比越大,因而随机场
中的占比越大,因而随机场 的波动约平缓。
的波动约平缓。


图 1一维随机场自协方差矩阵的特征函数(左)与特征值(右)
在获得一维随机场的特征函数和特征值后,基于方程(3)即可获得其自相关函数 。设一维随机场的长度l=1m,相关长度L=0.3m,则其自相关函数
。设一维随机场的长度l=1m,相关长度L=0.3m,则其自相关函数 如如图2所示。图 2(a)为式表示的自相关核函数,图 2(b)-(d)则是当求解过程中方程(3)取截断个数m=4、m=8和m=12时,分别获得的自相关函数。从图2中可见: 在对随机场进行K-L展开时,随着所取的展开截断项数m的增加,自相关函数
如如图2所示。图 2(a)为式表示的自相关核函数,图 2(b)-(d)则是当求解过程中方程(3)取截断个数m=4、m=8和m=12时,分别获得的自相关函数。从图2中可见: 在对随机场进行K-L展开时,随着所取的展开截断项数m的增加,自相关函数 越来越接近其自相关核函数,即自相关函数取得越精确,对随机场进行模拟的精度也越高。故在后面算例中,兼顾精度和计算工作量的情况下,拟选取截断个数为m=12。
越来越接近其自相关核函数,即自相关函数取得越精确,对随机场进行模拟的精度也越高。故在后面算例中,兼顾精度和计算工作量的情况下,拟选取截断个数为m=12。


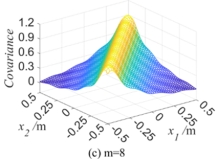

图 2 不同截断 值下,一维随机场的自相关函数图形(l=1m, L=0.3m)
值下,一维随机场的自相关函数图形(l=1m, L=0.3m)
对于二维高斯随机场,其特征值和特征函数可以用两个一维随机场的特征值和特征函数的乘积表示[3],具体表示如下
 (19)
(19)
 (20)
(20)
将式和式代入式可得到二维高斯随机场的K-L展开式
 (21)
(21)
3 结构不确定性量化
本文将基于所提出的高斯随机场模型,来表征结构参数的不确定性并对其量化。在有限元框架下,将结构参数的高斯随机场离散到每一个网格单元,并计算结构的随机动力特性;再利用核密度估计对结构的动力特性进行非参数估计,从而获得结构输出响应即结构随机动力特性的分布函数特征;最后将试验和模拟的输出响应分布特征进行对比,并对其结果做极大似然估计来量化模型的分布参数。
3.1 带有随机场参数的不确定结构动力特性分析
考虑结构的杨氏模量为高斯随机场变量,基于式对其进行离散后代入下述单元刚度矩阵和单元一致质量矩阵
 (22)
(22)
 (23)
(23)
其中 为几何矩阵,
为几何矩阵, 为形函数矩阵;
为形函数矩阵; 为积分区域,对杆单元和梁单元,
为积分区域,对杆单元和梁单元, 为单元长度,对于板壳单元,
为单元长度,对于板壳单元, 为单元面积;
为单元面积; 为结构材料的密度;对梁单元,
为结构材料的密度;对梁单元, 为式(24)所示的弹性矩阵,
为式(24)所示的弹性矩阵, 为梁的惯性矩;对薄板单元,
为梁的惯性矩;对薄板单元,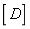 为式(25)所示的抗弯刚度矩阵,
为式(25)所示的抗弯刚度矩阵, 为材料的泊松比。
为材料的泊松比。
 (24)
(24)
 (25)
(25)
将单元刚度矩阵和单元质量矩阵组集并代入节点的边界条件,即可获得结构系统的总体刚度矩阵 和总体质量矩阵
和总体质量矩阵 。通常,对结构系统造成破坏的振动是低频振动,故本文在后续分析中,仅考虑系统低阶固有频率,并拟采用矩阵迭代方法进行求解,以便快速获得系统低阶固有频率及其对应的振型[6]。
。通常,对结构系统造成破坏的振动是低频振动,故本文在后续分析中,仅考虑系统低阶固有频率,并拟采用矩阵迭代方法进行求解,以便快速获得系统低阶固有频率及其对应的振型[6]。
设刚度矩阵 和质量矩阵
和质量矩阵 表示的结构系统为
表示的结构系统为 自由度正定系统,则采用柔度阵矩描述的结构系统自由振动运动方程为:
自由度正定系统,则采用柔度阵矩描述的结构系统自由振动运动方程为:
 (26)
(26)
设其解为 ,代入方程,得到如下所示的系统振型方程
,代入方程,得到如下所示的系统振型方程
 (27)
(27)
令 ,则式可变为如下的特征值表达式
,则式可变为如下的特征值表达式
 (28)
(28)
对于第一阶特征值,有 ,基于此关系采用矩阵迭代法是进行反复迭代,最终可求出最大特征值
,基于此关系采用矩阵迭代法是进行反复迭代,最终可求出最大特征值 和对应的特征向量
和对应的特征向量 ,其迭代步骤如下:
,其迭代步骤如下:
1) 取任意的基准化振型 作为初始试解向量,按式
作为初始试解向量,按式 进行第一次迭代,其中
进行第一次迭代,其中 和
和 的第一个分量均被基准化为1。
的第一个分量均被基准化为1。
2) 若 ,将
,将 作为试解向量赋值给
作为试解向量赋值给 ,再重复进行步骤1)的操作,直到第k次迭代
,再重复进行步骤1)的操作,直到第k次迭代 ,若此时
,若此时 ,则表明迭代收敛,则有:
,则表明迭代收敛,则有: ,
, 。在实际迭代过程中因存在误差而不能得到理想结果
。在实际迭代过程中因存在误差而不能得到理想结果 ,使得
,使得 ,也意味着迭代收敛,其中err为选定的误差阈值。
,也意味着迭代收敛,其中err为选定的误差阈值。
对第二阶及其更高阶的特征值和特征向量的求解,需对动力矩阵 进行清型,即利用主振型的正交性,对
进行清型,即利用主振型的正交性,对 进行修正,将
进行修正,将 中的前r阶主振型的成分清除掉,从而得到第(r+1)阶的迭代动力矩阵。依据泛函理论中的投影定理,拟采用的清型矩阵为
中的前r阶主振型的成分清除掉,从而得到第(r+1)阶的迭代动力矩阵。依据泛函理论中的投影定理,拟采用的清型矩阵为
 (29)
(29)
其中 ,令:清型前后的动力矩阵分别为
,令:清型前后的动力矩阵分别为 和
和 ,具体清型过程实施如下
,具体清型过程实施如下
 (30)
(30)
对 再次实施上述清型即进行迭代计算,即可获得系统的第r+1阶特征值
再次实施上述清型即进行迭代计算,即可获得系统的第r+1阶特征值 及其对应的特征向量
及其对应的特征向量 ,进一步可求得系统的第r+1阶固有频率
,进一步可求得系统的第r+1阶固有频率 。
。
3.2 多维核密度估计
极大似然估计提供了一种给定观察数据来评估模型参数的方法,即模型已定,参数未知。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。由于模型输出响应的分布特征未知,故需对输出响应的概率分布首先做非参数估计,本文拟采用多维核密度估计法对输出响应的概率分布进行非参数估计。
当考虑结构参数是随机场变量时,模型的固有频率 (
(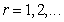 )为也随机变量且设其为独立同分布随机变量,令其分布密度函数的多维核密度估计为[8]:
)为也随机变量且设其为独立同分布随机变量,令其分布密度函数的多维核密度估计为[8]:
 (31)
(31)
其中 ,
, 为
为 的样本数据,
的样本数据, 为样本数据的均值;
为样本数据的均值; 为样本
为样本 的协方差矩阵,
的协方差矩阵, 为
为 的特征向量方阵;
的特征向量方阵; 为多元核函数;
为多元核函数; 为窗宽矩阵,选择的原则是使得计算结果均方误差最小;核密度估计点
为窗宽矩阵,选择的原则是使得计算结果均方误差最小;核密度估计点 ,
, 为向量,表示核密度估计函数的自变量,就本文而言,该自变量向量是指结构输出响应
为向量,表示核密度估计函数的自变量,就本文而言,该自变量向量是指结构输出响应 通过
通过 变形后得到的向量
变形后得到的向量 。
。
3.3 极大似然估计
对结构模型的输出响应做极大似然估计,估计出满足概率分布密度的参数,把可能性最大的那个参数 作为真实参数
作为真实参数 的估计量。由于对数似然函数更易计算,故对式(31)所示的核密度估计函数,将其用对数似然函数表示为:
的估计量。由于对数似然函数更易计算,故对式(31)所示的核密度估计函数,将其用对数似然函数表示为:
 (32)
(32)
式中 为一个超参数,即
为一个超参数,即 ,
, 为高斯随机场的标准差,
为高斯随机场的标准差, 为高斯随机场的相关性长度;模拟输出响应
为高斯随机场的相关性长度;模拟输出响应 ,
,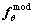 为模型在超参数
为模型在超参数 下的输出响应,样本
下的输出响应,样本 的协方差矩阵为
的协方差矩阵为 ,
, 为
为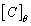 的特征向量方阵;
的特征向量方阵; ,
, 为试验输出响应;
为试验输出响应; 为试验的点数。根据多元高斯分布的核函数假设[8],取窗宽如下
为试验的点数。根据多元高斯分布的核函数假设[8],取窗宽如下
 (33)
(33)
其中 为协方差矩阵
为协方差矩阵 的特征值矩阵。
的特征值矩阵。
取如下的高斯核函数
 (34)
(34)
采用极大似然估计法对试验样本的分布参数进行量化估计验证,即先假定一组参数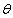 ,经过数值计算得到每一组参数样本的输出响应并作为模型样本,对响应值进行核密度估计即基于式(31)得到输出响应的概率分布密度函数后,将试验样本和模型样本的输出响应带入式得到极大似然估计函数
,经过数值计算得到每一组参数样本的输出响应并作为模型样本,对响应值进行核密度估计即基于式(31)得到输出响应的概率分布密度函数后,将试验样本和模型样本的输出响应带入式得到极大似然估计函数 ,进而得到似然函数最大值处的参数
,进而得到似然函数最大值处的参数 ,并验证
,并验证 是否为试验样本参数
是否为试验样本参数 。
。
4 算例验证
4.1 工字梁算例验证


(a) (b)
图3 10号工字梁截面尺寸(a)和简支梁的有限元划分(b)
长度为1 、截面为工字型的简支钢梁见图3,选用10号工字梁,其惯性矩
、截面为工字型的简支钢梁见图3,选用10号工字梁,其惯性矩 ,截面积
,截面积 ,单位长度质量密度
,单位长度质量密度 ,材料弹性模量210
,材料弹性模量210 。将梁划分为60个梁单元进行分析,如图3(b)所示。
。将梁划分为60个梁单元进行分析,如图3(b)所示。
令梁材料弹性模量 为随机场,均值为
为随机场,均值为 ,协方差函数取为
,协方差函数取为 ,通过式(1),采用K-L展开得到每一单元的弹性模量为:
,通过式(1),采用K-L展开得到每一单元的弹性模量为:

从式(35), 的不确定随机场就由标准差
的不确定随机场就由标准差 及相关长度
及相关长度 组成的超参数
组成的超参数 来表征,即超参数
来表征,即超参数 为试验样本和模型样本的输入参数,通过数值实验来量化弹性模量随机场。基于3.1部分,可求出每一根工字梁的前八阶固有频率,并将其组成固有频率矩阵
为试验样本和模型样本的输入参数,通过数值实验来量化弹性模量随机场。基于3.1部分,可求出每一根工字梁的前八阶固有频率,并将其组成固有频率矩阵 。
。
给定一个输入参数 ,取500根梁的固有频率矩阵
,取500根梁的固有频率矩阵 为试验数据样本;此外,另取一组超参数
为试验数据样本;此外,另取一组超参数
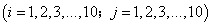 ,具体参数值取为
,具体参数值取为 ,
,
 ,针对每一个超参数
,针对每一个超参数 均取100根梁的固有频率组成模型矩阵样本
均取100根梁的固有频率组成模型矩阵样本 ,总计采用的梁为10000根,共计100个模型矩阵样本
,总计采用的梁为10000根,共计100个模型矩阵样本 。基于梁的固有频率的试验样本
。基于梁的固有频率的试验样本 和100个模型样本
和100个模型样本 ,对固有频率进行核密度估计和极大似然估计,从而验证超参数
,对固有频率进行核密度估计和极大似然估计,从而验证超参数 的可辨识性和随机场模型的有效性。
的可辨识性和随机场模型的有效性。
4.1.1 实验数据分析
分别针对弹性模量的四个超参数 、
、 、
、 和
和 ,计算每个超参数下10根梁上单元弹性模量
,计算每个超参数下10根梁上单元弹性模量 的随机过程分布,如图4所示,其中每一条曲线表示一根梁上各单元弹性模量取值大小分布,反映了同一根梁上各点处弹性模量取值的随机性。由图可见:弹性模量随机场的取值均围绕其均值210GPa上下波动,纵轴的波动反映了方差的大小及其方差随梁轴向尺寸的变化;正如超参数中
的随机过程分布,如图4所示,其中每一条曲线表示一根梁上各单元弹性模量取值大小分布,反映了同一根梁上各点处弹性模量取值的随机性。由图可见:弹性模量随机场的取值均围绕其均值210GPa上下波动,纵轴的波动反映了方差的大小及其方差随梁轴向尺寸的变化;正如超参数中 和
和 的含义,均方差
的含义,均方差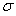 对于梁的弹性模量随机分布的影响要远大于相关长度
对于梁的弹性模量随机分布的影响要远大于相关长度 对的影响;超参数相同的情况下,每一图中10条曲线即弹性模量随机场分布的差异非常明显,但由于同属一个超参数,因而其总体分布规律相似。基于图4的结果,在后续分析中拟采用超参数
对的影响;超参数相同的情况下,每一图中10条曲线即弹性模量随机场分布的差异非常明显,但由于同属一个超参数,因而其总体分布规律相似。基于图4的结果,在后续分析中拟采用超参数 进行分析。
进行分析。
由图可见:对于梁的弹性模量随机场分布而言, 的变化对弹性模量总体取值随机分散性的影响很小,但是
的变化对弹性模量总体取值随机分散性的影响很小,但是 直接影响各梁单元随机性分布,即
直接影响各梁单元随机性分布,即 越大,弹性模量沿梁长度方向的取值波动越剧烈。
越大,弹性模量沿梁长度方向的取值波动越剧烈。




图4 梁的杨氏模量随机场分布
4.1.2 一维核密度估计
为验证所选超参数 的适用性,选取梁的第二阶固有频率的试验样本
的适用性,选取梁的第二阶固有频率的试验样本 和模型样本
和模型样本 ,分别对第二阶固有频率作单一参数的一维核密度估计。
,分别对第二阶固有频率作单一参数的一维核密度估计。
首先,固定 中的
中的 ,取
,取 时,有10个
时,有10个 ,针对每个
,针对每个 相应的100根梁,求解其第二阶固有频率并构成模型样本
相应的100根梁,求解其第二阶固有频率并构成模型样本 ,然后取
,然后取 和
和 的100根梁的第二阶固有频率构成试验样本
的100根梁的第二阶固有频率构成试验样本 ,基于
,基于 和
和 的数据可得到的结构第二阶固有频率的一维核密度估计如图5(a)所示。由图5(a)可见:固定相关性长度L时,模型样本固有频率的分布随着杨氏模量均方差
的数据可得到的结构第二阶固有频率的一维核密度估计如图5(a)所示。由图5(a)可见:固定相关性长度L时,模型样本固有频率的分布随着杨氏模量均方差 的减小变得越来越集中,当试验样本的标准差与模型样本的标准差均为
的减小变得越来越集中,当试验样本的标准差与模型样本的标准差均为 时,两者固有频率的分布最为接近。
时,两者固有频率的分布最为接近。
同样地,固定 中的
中的 ,取
,取 ,取 100根梁,求解其第二阶固有频率并构成模型样本数据
,取 100根梁,求解其第二阶固有频率并构成模型样本数据 ,另外再取
,另外再取 和
和 的试验样本数据
的试验样本数据 ,对第二阶固有频率
,对第二阶固有频率 的一维核密度进行估计,如图5 (b)所示。由图5(b)可见:固定标准差
的一维核密度进行估计,如图5 (b)所示。由图5(b)可见:固定标准差 时,模型样本固有频率的分布随着相关长度L的减小越来越集中,当试验样本的相关性长度与模型的相关性长度相等时,两者固有频率的分布最为接近;再一次,图5显示出参数均方差对于固有频率核密度波动的影响要大于相关长度对其的影响。
时,模型样本固有频率的分布随着相关长度L的减小越来越集中,当试验样本的相关性长度与模型的相关性长度相等时,两者固有频率的分布最为接近;再一次,图5显示出参数均方差对于固有频率核密度波动的影响要大于相关长度对其的影响。


(a)  (b)
(b) 
图 5 仅考虑弹性模量为随机场变量时第二阶固有频率的一维核密度估计
类似地,同时考虑弹性模量和质量密度为随空间尺寸变化的随机场,其超参数均取为 ,取100根梁,对其第二阶固有频率
,取100根梁,对其第二阶固有频率 的一维核密度再次进行估计。其中,固定
的一维核密度再次进行估计。其中,固定 且
且 ,左图为质量密度随机场相关长度
,左图为质量密度随机场相关长度 ,但
,但 变化时估计出的
变化时估计出的 的一维核密度分布函数;右图为固定弹性模量随机场的相关长度
的一维核密度分布函数;右图为固定弹性模量随机场的相关长度 ,但
,但 变化时估计出的
变化时估计出的 的一维核密度。当固定
的一维核密度。当固定 时,(c)图是
时,(c)图是 =
= ,
, 变化时对
变化时对 的一维核密度分布函数的估计;图(d)是当
的一维核密度分布函数的估计;图(d)是当 ,
, 变化时估计出的
变化时估计出的 的一维核密度分布函数。
的一维核密度分布函数。
从图中可见, 和
和 对
对 核密度分布函数的影响明显大于
核密度分布函数的影响明显大于 和
和 的影响;其他参数固定,
的影响;其他参数固定, 和
和 两者分别变化时,
两者分别变化时, 对
对 核密度分布函数的影响要大于
核密度分布函数的影响要大于 的影响;其他参数固定,
的影响;其他参数固定, 和
和 两者分别变化时,
两者分别变化时, 对
对 核密度分布函数的影响更大。总体上,质量密度随机场比弹性模量随机场对
核密度分布函数的影响更大。总体上,质量密度随机场比弹性模量随机场对 核密度分布函数的影响更大。
核密度分布函数的影响更大。


(a)  (b)
(b) 


(c)  (d)
(d) 
图 6同时考虑弹性模量和质量密度为随机场变量时四阶固有频率的一维核密度估计
4.1.3 多维核密度估计及最大似然估计
为更准确验证所建随机场模型的有效性和超参数的可辨识性,有必要对结构输出响应进一步进行多维核密度概率分布函数的估计,进而基于此进行极大似然估计来获得似然函数取得最大值时所对应的超参数值。
当弹性模量为随机场时,首先对来自500根梁的试验数据 和10000根梁的100个模型矩阵样本数据
和10000根梁的100个模型矩阵样本数据 进行梁的前8阶固有频率的八维核密度估计,进而基于公式(32)对参数
进行梁的前8阶固有频率的八维核密度估计,进而基于公式(32)对参数 进行极大似然估计,其中
进行极大似然估计,其中 和
和 均由结构的前八阶固有频率构成。由于部分点的概率密度函数值较小,为避免连乘时似然函数的计算值为0,需先对概率密度函数值取对数后再连加。获得的对数似然函数的三维图形如图7所示。
均由结构的前八阶固有频率构成。由于部分点的概率密度函数值较小,为避免连乘时似然函数的计算值为0,需先对概率密度函数值取对数后再连加。获得的对数似然函数的三维图形如图7所示。
图7(a)为试验数据样本超参数取为 时前8阶固有频率的对数似然函数
时前8阶固有频率的对数似然函数 的图像,可见对数似然函数
的图像,可见对数似然函数 取极大值时,对应点的参数
取极大值时,对应点的参数 为
为 ,说明所引入的随机场模型能很好地识别模型参数,即该随机场模型是可靠的。
,说明所引入的随机场模型能很好地识别模型参数,即该随机场模型是可靠的。
全套毕业设计论文现成成品资料请咨询



