摘要:当车辆路径应用在配送中心的各个分支机构进行配送时,我们使用了介于快递和托收之间的分配销售战略。它假定车辆在各个点之间的配送时间服从正态分布,在软时间窗口约束条件下各个分布地点的配送接收数量服从泊松分布,这篇文章建立了解决方案模型并进行了遗传算法求解的应用程序设计。采用遗传算法通过优化排序和基于最优化个体的选择策略以及自适应交叉概率的参数控制以保证结果的有效性。同时使用Matlab设计了算例实验,以验证提出的方案的可行性。
关键词:物流配送;GA:电子商务;VRP
Ⅰ. 绪论
随着中国社会经济和电子商务行业的不断发展,快递行业作为一个新兴产业也有了快速发展的机遇,各种快递行业也越来越多地出现。在国际快递公司迅速进入中国市场同时,市场竞争越来越严峻,国内快递公司面临着严峻的考验。所以快递公司迫切需要解决第一个问题是:我们的国家快递物流如何在这场激烈的竞争中生存和不断发展。在这样的形势下,(车辆路径问题)VRP在现实生活中得到了广泛的应用,也为快递物流公司在配送过程中制定合理的车辆配送路径提供了科学依据。
Edstein [1]是最早从理论上系统研究VRP的人,也是最早采用启发式算法解决多车辆和时间窗的限制问题。 Feng [2]也采用多算法来解决时间窗和双向分布的多状态约束问题,并深入分析了使用计算机进行遗传算法的参数求解结果影响。Klipp [3]在动态信息条件下更全面地分析和解决了VRP。在实际问题中不同的约束条件和不同条件组合后的车辆路径存在一定的差异[4]。毫无疑问,这些条件将根据实际应用中的实际问题来设定,并且有利于使用遗传算法来解决这些问题。本文在介绍电子商务与物流配送的理论、发展前景、趋势与特点的基础上,阐述了电子商务与物流的关系,总结了电子商务模式下物流配送的主要模式。通过优化车辆路线、提高发车准时率、提高快递接待数量从而改善快递公司配送效率。在某一家快递公司的实证分析中,该公司的分销网络系统是新计划的。实验分析表明,该算法具有较好的收敛性和稳定性,能够有效地解决这种约束下的车辆路径分配问题。
Ⅱ. 数学模型在优化中的应用
车辆路径问题(VRP) 是指在路径网络中有一系列的分布点。他们需要最低总成本和最短时间消耗的限制条件下,如车辆负荷重量、交货时间和驾驶距离限制的情况下,组织车辆沿适当的车辆路线按顺序传递以最短总路线到达目的地[5]。在实际问题中, 通常研究配送中心对各需求点分布的路径,使其在满足一定条件下达到一个或多个目标。这种分配路径安排将会被优化。
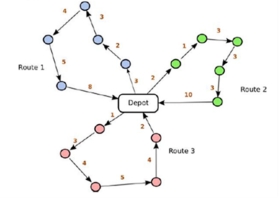
图1 VRP问题的示意图
假设一家快递公司将为多个配送点配送快件,配送中心配有多辆配送车辆。 每辆车的承载重量与给定的相同,所选择的车辆数量以及每辆车的路线都是未知的。分布式车辆从该中心开始,在任务完成后按车辆符合范围分配并返回分配中心。图1描绘了4辆车的行车路线分布。本文采用车辆行驶总距离来衡量快速分布。总距离越短,分布项目越优化[6]。
对于VRP问题,我们建立了具有最短分布路径对象的数学模型。在该模型中,配送中心的代码为0,快递配送点代码为1, 2, … , n。配送中心和快递配送点都由i(i =0, 1, … , n)表示。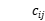 表示客户i到j的运输成本。
表示客户i到j的运输成本。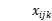 表示从i到j的车辆k, 以及
表示从i到j的车辆k, 以及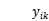 表示请求点i由k服务,如以下等式所述:
表示请求点i由k服务,如以下等式所述:
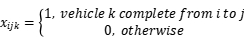 (1)
(1)
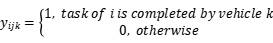 (2)
(2)
约束条件如下所示:
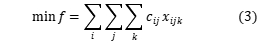
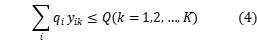
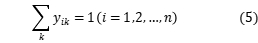

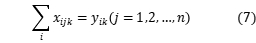
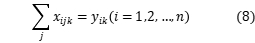
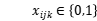 ,
,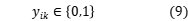
目标函数3表示总分布的最短路径;约束4是车辆载荷能力约束,即每个分配中车辆的最大载荷;约束条件5确保每个客户都可以被服务;约束条件6确保每辆汽车从配送中心开始并返回配送中心;约束条件7和8确保客户端i,j在行驶路径上以及由车辆k服务他们;约束9定义了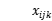 和
和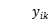
Ⅲ. 基于遗传算法优化的物流配送模型
遗传编码与初始种群生成
本文采用遗传算法求解多目标VRP模型。由于遗传算法不能直接解决实际问题,因此首要工作就是对问题求解进行编码,并在染色体的构建表达与实现之间形成一一对应的关系。遗传算法的编码方法主要包括二进制编码,浮点编码和符号编码。就车辆路径而言,本文将采用自然数字符号进行编码。自然数字编码将问题解决方案解码为k+ m+ 1长度的自然数阵列。编码中的每个染色体都指潜在解决方案中的一个初始解。
主要种群的规模和质量将在很大程度上影响算法的最终解决方案质量。为保证初始种群具有最优性质,算法具有较快的收敛性,初始种群可以从1到N初始生成个数,以n个个体等级作为初始染色体,代表n个客户随机排列分配序列。
适应度函数评价
对于多目标模型的适应度函数设计,多目标函数需要初始化为单目标函数。 如果直接采用线性加法,就容易产生维数不统一,需要专门将多目标函数转换为无量纲变量。
首先,目标函数10,11和12是由等式13,14和15转换,这将对象函数值改变为无量纲变量:
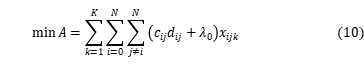
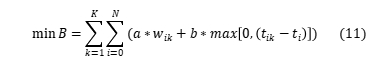

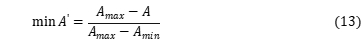
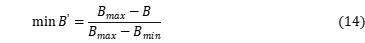

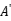 ,
,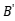 和
和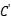 是无量纲变量对象函数函数值,他们的范围是0-1,
是无量纲变量对象函数函数值,他们的范围是0-1,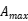 ,
,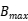 ,
,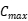 ,
, 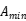 ,
,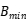 和
和 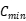 是每代遗传算法的最大值和最小值。
是每代遗传算法的最大值和最小值。
最后我们采用权重比来获得所需要的适应函数:
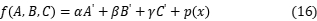
 ,
, 和
和 是重量参数
是重量参数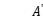 ,
, 和
和 ,其数值范围均为0-1。
,其数值范围均为0-1。
本文以城市快速配送为研究重点, 对人口最优自适应价值快运公司的运营成本、服务时间和表达过程的认识,应根据实际需求,建立在重量分配或相应调整的基础上。
选择算子
选择算子是确定涉及下一代遗传交叉群的策略。适应性越强,组的选择概率越大。这可以促进完美的个体产生下一代,但太多完美的个体会导致更差的种群变化,并且算法会在早期的局布优化中快速收敛。为了克服上述缺陷,可以应用基于适应度排名的选择算子排列。具体方法如下:所有的临时个体都将根据其适应度排序来提升序号和数量,每条染色体的序列号将被视为新的适应度值。假设:X个个体,适应值为1,2,3, ... x, 待选择的i染色体概率为:
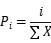
对于这种改进的选择算子,在选择概率和个体适应性值之间存在着相对大小的关系,这样种群就可以在世代遗传中保持多样性和最佳特性。同时,为了使最优染色体能够生成下一代,将采用最优染色体的保留策略。
交叉和突变
本文采用局部映射交叉,从双群体中的第一条染色体开始。如果每个染色体和随机生成的数目小于或等于交叉概率,则第一个染色体的两个末端数目不会改变。在中间随机选择一个部分进行交换,第二个染色体随机选择一个部分进行交换,否则该染色体将不进行交叉操作。对于交叉操作,如果第一条染色体在交叉部分存在冲突数,则两条染色体将在一一对应交换中相互交叉直到交叉结束。需要说明的是,本文中的映射交叉是第一种和第二种之间的交叉,而不是第一个和第二个之间的交叉。
变异算子主要用于避免变异操作落入局部优化并改变种群进化。常见的变异算子包含基准标准变异,反转变异和均习变异,本文采用2-exchange突变。具体操作是随机选择一条染色体,随机获取中间部分的两个基因进行交换,最终得到一个新的个体。
Ⅳ.案例分析
为了验证本文遗传算法的有效性和可行性,我们将采用比较分析。针对相关参考文献中具体的多目标优化案例,本文采用汇编软件Visual C+ 6.0进行计算和实现算法,并比较最终的运行结果和参考文献。如果操作实现结果优化,则说明本文的算法在求解路径优化方面具有一定的操作性和可行性。
一个公司内有一个配送中心为80个客户点配送,每个客户点的坐标和需求量如表1所示。该公司有2种配送车型,车辆数量分别为11和2。最大允许容量分布为500和400。客户需求的时间窗为9: 00-11: 00,软时间窗为11: 30-13: 00和14: 00-17: 00。该公司从9:00开始,并先后分配分配路线安排。
表1 客户坐标分布表
|
Client NO.
|
Coordinate
|
Demand
|
|
1
|
(37,50)
|
7
|
|
2
|
(49,49)
|
30
|
|
3
|
(52,64)
|
16
|
|
4
|
(20,25)
|
9
|
|
5
|
(40,29)
|
21
|
|
6
|
(21,46)
|
15
|
|
7
|
(17,63)
|
19
|
|
8
|
(31,61)
|
23
|
|
9
|
(52,33)
|
1
|
|
10
|
(51,22)
|
5
|
|
11
|
(41,42)
|
19
|
|
12
|
(31,31)
|
29
|
|
…
|
…
|
…
|
改进后的GA用于连续不断计算10次,一次驾驶的最短时间为110分钟。相应分部的虚拟路径如图2所示。红色路径指的是第一条分发路径,蓝色路径指的是第二条分发路径。也就是说,从配送中心开始,根据图形分配逐步完成两个循环。10倍计算一次性人口优化适应性的变化如图3所示。
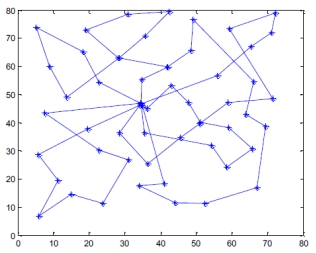
图2 VRP问题示意图
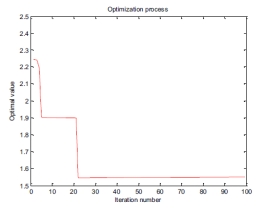
图3 人口最优适应值变化过程
连续10次GA的耗时如图4所示,从图中可以看出,GA计算时间为79~80秒,计算时间可以接受,而图4也表明优化过程中分布时间有效缩短。如果考虑到车辆在高峰时段交通堵塞的情况下按照路径行驶,则它们也会在10:15出发,并且在将各个客户的点分配到集散中心之后将全程消耗190分钟。比道路网时间变化特征下的路径分布优化多消耗81分钟。
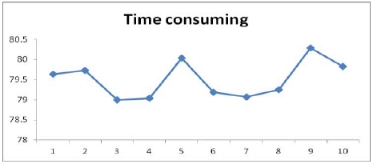
图4 10次连续操作示意图
Ⅴ. 结论
随着消费者更倾向于未来的购物模式,快递企业必须遵循促进电子商务的发展和趋势。根据快递的分布特点,本文以短车行驶路线为例,以快递和短时间罚款为目标,在软时间窗条件下建立配送车辆路径模型,并根据模型设计了遗传算法限制。最后证明了该算法具有良好的收敛性和稳定性,有效地解决了该约束条件下的车辆路径分配问题。对于快递配送中心来说,安排合适的车辆,优化出发时间和组织车辆路径对于节约运输成本,提高配送效率具有重要意义。



