Express Logistics Distribution Model Optimization for E-commerce Environment

Yang Ming

Chongqing College of Electronic Engineering, Chongqing China, 401331

Abstract：When vehicle path is performing express distribution for various branches in distribution center, we adopt simultaneous service of distribution strategy between express delivery and collection. It assumes that vehicles follow normal distribution of travel time among each point. Under condition that distribution branches have soft time window restriction and express delivery collection quantity follows Poisson distribution, the paper establish solution model of problems and performs genetic algorithm solution-based application design. GA algorithm is adopted to ensures the result effectiveness through fitness ranking and optimal individual-based selection strategy as well as parameter control of adaptive crossover probability. We also design numerical example with Matlab for experiment to prove the feasibility of our scheme.

Keywords：logistics distribution; GA; e-commerce; VRP

Ⅰ. INTRODUCTION

With constant development of Chinese social economy and e-commerce industry, express delivery industry also has rapid development opportunity as a new industry and various express delivery industries increasingly appear. While international express delivery companies rapidly and increasingly enter Chinese market and market competition is gradually serious, domestic express delivery companies confront severe test. Express delivery companies urgently need to solve the first problem: how our national express logistics survive and constantly develop in this severe competition. (Vehicle Routing Problem) VRP is broadly applied in real life and it can also provide scientific basis for express logistics companies to formulate reasonable vehicle distribution path during distribution.

Edstein [1] is the earliest person to study VRP systematically in theory as well as algorithm and uses heuristic algorithm to solve basic problems of restriction such as multi-vehicle and time window. Feng [2] also uses multi-algorithm to solve multi- condition restriction on time window and two-way distribution and deeply analyzes solution results effect in terms of calculator and parameter in genetic algorithms. Klipp [3] more comprehensively analyzes and solves VRP under dynamic information condition. There are different restriction conditions in practical problems and there are some differences between vehicle paths after different conditional combination [4]. There is no doubt that these conditions will be set according to practical problems in practical application and it has advantages to use genetic algorithm to solve these problems. Based on introducing theory, development prospect, tendency and characteristics of e-commerce and logistics distribution, this paper illustrates relationship between ecommerce and logistics and summarizes the main modes of logistics distribution under e-commerce mode. Then the vehicle path will be used for express corporation distribution and distribution efficiency in Express Corporation will be improved through optimizing vehicle route, increasing departure punctuality and improving express delivery reception quantity. In terms of empirical analysis in one express corporation, distribution network system in this corporation is newly planned. The experimental analysis shows that this solution algorithm has better convergence and stability so it can effectively solve distributing vehicle path in this restriction.

Ⅱ. MATHMATICAL MODEL IN PATH OPTIMIZATION

Vehicle routing problem(VRP) means that there are a series of distributing points in path network. They need to organize vehicles to pass in sequence along appropriate vehicle route and reach the purpose such as the shortest total route [5], the lowest total cost and the shortest time consumption under certain restricting conditions such as vehicle load weight, delivery time and driving distance limitation. In practical problem, it usually studies the path of distribution center to various requirement point distribution so that it reaches one or more targets under satisfying certain conditions. This distributing path arrangement will be optimized.

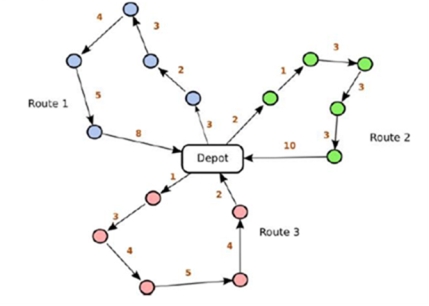
Figure 1. Sketch map of VRP problem

It is supposed that one express corporation will distribute express for several distributing points and distributing center has several distribution vehicles. The bearing weight of each vehicle is the same as well as given and the selected vehicle quantity as well as each vehicle route is unknown. The distributed vehicle starts from this center, distributes in vehicle load range and returns distributing center after task completion. Figure 1 depicts the driving path distribution of 4 vehicles. This paper adopts total distance of vehicle driving to measure express distribution. The shorter the total distance is, the more optimal the distribution project is [6].

For VRP problem, we establish the mathematical model with the object of the shortest distribution path. In the model, the code of distribution center is 0 and the express delivery point code is 1, 2, ..., n. The distribution center and express delivery point are all denoted by i (i = 0, 1, ..., n). 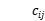 denotes the transportation cost from client i to j.  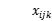denotes vehicle k from i to j, and  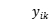denotes demand point i is served by k, as described by the following equations:

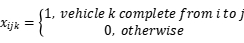          (1)

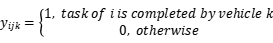      (2)

The constraint condition are shown as follows:

,

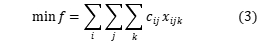
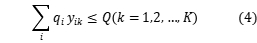
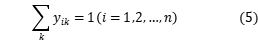
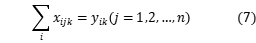
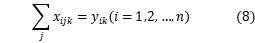
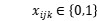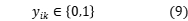
Objection function 3 denotes the shortest path of total distribution; constraint 4 is vehicle loading capacity constraint, that is, the maximum loading of vehicle in each distribution; constraint 5 ensures each client can be served; constraint 6 ensures each vehicle starts form distribution center and returns to distribution center; constraints 7 and 8 ensures the client i, j on the driving circuit, and the served of them by vehicle k ; constraint 9 defines the range of 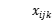 and .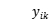

III. GA OPTIMIZATION-BASED EXPRESS LOGISTICS DISTRIBUTION MODEL

Genetic Coding and Initial Population Generation

GA is used to solve multi-target VRP model in this paper. Since GA cannot directly solve practical problems, the primary job is to encode problems solution and form one-to-one correspondence relationship between expression and realization in chromosome. The coding method of GA mainly includes binary code, float encoding and sign coding. As far as vehicle path, this paper will adopt natural number symbol to encode. Natural number coding decodes problems-solution as a natural number array in k+m+1 length. Each chromosome in coding refers to one initial solution in potential solution.

The scale and quality of primary population will largely affect final solution quality of algorithm. In order to guarantee that initial population has optimal property and algorithm has fast convergence, initial population can initially generate number from 1 to N and take n numbers of ranking as initial chromosome to stand for n customers’ random arrangement of distributing sequence.

Fitness Function Evaluation

For fitness function design of multi-target model, multitarget function needs to be initially transformed into single target function. If it directly adopts linear addition, this will easily generate dimension disunity so it needs to specially transform multi-target function into dimensionless variable.

First the object functions 10, 11, and 12 are converted by equation 13, 14, and 15, which changes the object function value to dimensionless variables:

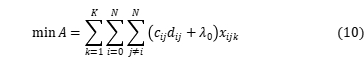
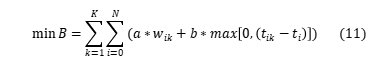
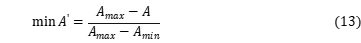
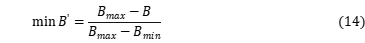
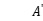, and are object function value of dimensionless variables and their range is 0-1;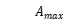, , 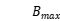, , 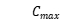 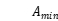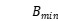and 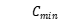 are maximum and minimum value of GA colony of each generation.

Finally we adopt weigh ratio to get needed fitness function:

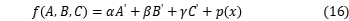
, and  are weight parameters of 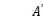, and  and their value range are all 0-1.

Since this article focuses on the urban express distribution, recognition of operating cost, service time and express process changing of the population optimal adaptive value express corporation should be based on weight distribution or correspondingly adjustment according to practical requirement.

Selection Operator

Selection operator is the strategy to determine involving genetic crossover group in next generation. The stronger the fitness, the larger the selected probability of group. This can promote the perfect individual to generate the next generation but too many perfect individuals will result in worse population variety and algorithm will quickly converge in local optimization in prematuriy. In order to overcome above deficiencies, fitness ranking-based selecting operator array can be applied. The detailed methods are depicted as follows: all temporary individuals will ascend orderly and number according to its fitness value and serial number of each chromosome will be taken as new fitness value. Suppose: there are X individuals and fitness values are 1,2,3,…,X and the i chromosome probability to be selected is: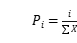. For such improved selection operator, there is relationship of relative size between selection probability and individual fitness value so that population can keep variety and optimal property in generational genetics. Meanwhile, in order that the optimal chromosome can generate to the next generation, the keeping strategy of optimal chromosome will be adopted.

Crossover and Mutation

This paper adopts partial mapping crossover and starts from the first chromosome in population with double-group. If each chromosome and randomly generating number are smaller than or equal to crossover probability, two ends number of the first chromosome will not change. One random part in the middle is selected for crossover and exchange and the second chromosome is randomly selected one part for exchange or this chromosome will not be performed crossover operation. For crossover operation, if the first chromosome has conflict number in crossover section, two chromosomes will be mutually in one-to-one correspondence exchange till crossover is over. It needs to be explained that the mapping crossover in this paper is the crossover between the firsts and the seconds but not between the first and the second.

Mutation operator is mainly used to avoid mutation operation to fall into local optimization and modify population evolution. Common mutation operators contains base standard mutation, inversion mutation and uniform mutation and this paper adopts 2-exchange mutation. Specific operation is to randomly select one chromosome, randomly get two genes in middle part for exchange and finally get a new individual.

IV. CASE ANALYSIS

In order to verify effectiveness and feasibility of genetic algorithm in this paper, we will adopt comparison analysis. With specific multi-target optimization cases in relevant references, this paper uses assembly software Visual C++6.0 to calculate and realize algorithm and compares final operating results and references. If operation achieves results optimization, it indicates that algorithms in this paper have operations and feasibility in solving path optimization.

There is one distribution center in one company for 80 clients points, coordinates and demand quantity of each customer point is shown as table 1. This company has 2 kinds of distributing vehicle types and vehicle quantities are respectively 11 and 2. The most allowable capacities in distribution are 500 and 400. The time window in customer’s requirement is 9:00-11:00, and soft time windows are 11:30-13: 00 and 14: 00-17:00. The company starts from 9:00 and successively assigns distributing routing arrangement.

Table 1. Distribution of client points

The improved GA is used to constantly calculate 10 times and the shortest time of one-time driving is 110 minutes. Virtual path of corresponding distribution is shown as figure 2. Red path refers to the first distribution path and blue path refers to the second distribution path. That is, starting from distribution center, distribution is gradually completed by two loops according to the figure. The change of one-time population optimization fitness in 10 times calculation is shown as figure 3.

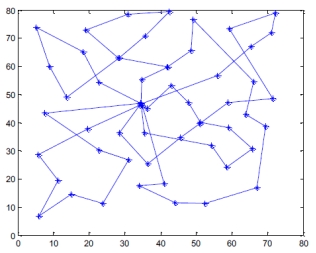
Figure 2. Sketch map of VRP problem

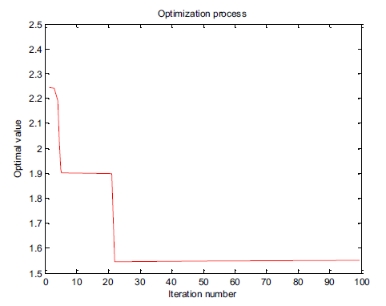
Figure 3. Process changing f the population optimal adaptive value

The time consumption of continuously 10 times of GA is shown in figure 4. From it we can see that GA takes 79-80 seconds in calculation and calculating time can be acceptable while figure 4 also shows distributing time effectively shortens during optimization. If vehicles drive according to path with consideration of traffic jam in peak period, they also depart in 10:15 and it will consume 190 minutes in the whole journey after distributing various customers’ points to distributing center. It consumes 81 minutes more than optimizing path distribution under time variance characteristics in road network.

Figure 4. Comparison with 10 times of consecutive operations

V. CONCLUSIONS

As consumers’ more preferring shopping mode in future, express corporations must follow to promote e-commerce development and its development. According to express distribution characteristics, this paper takes short vehicle driving path, many fetching express delivery and short time punishment as target, sets up distribution vehicle path model under conditions of soft time window, simultaneous delivery and shipping restriction and designs genetic algorithm according to model restriction. Finally, this paper proves that this algorithm has perfect convergence and stability so it effectively solves distributing vehicle path under this restriction. It is significant for express distribution center to arrange suitable vehicles, optimize departure time and organize vehicle path so as to save transportation cost and improve distribution efficiency.