AN ADAPTIVE TABU SEARCH APPROACH FOR BUFFER ALLOCATION PROBLEM IN UNRELIABLE PRODUCTION LINES

Abstract: The buffer allocation problem, i.e. how much buffer storage to allow and where to place it within the line, is an important research issue in designing production lines. In this study, buffer allocation problem is solved for unreliable non-homogeneous production lines. The objective is to maximize the throughput of the line under buffer capacity constraints. To evaluate the throughput of the line the decomposition method is employed. An adaptive tabu search approach is proposed to optimize the buffer sizes for each location. The performance of the proposed approach is evaluated by the computational tests.

Keywords: buffer allocation problem, production lines, adaptive tabu search, combinatorial optimization.

1. Introduction

A production line consists of a serial arrangement of machines and buffer areas that divide the line into stages. The performance of a production line is affected by both variations of the processing times and the reliability parameters of the machines. The effects of such variations can be reduced by using interstage buffers between the machines.

The buffer allocation problem deals with finding optimal buffer sizes to be allocated into the buffer areas in a production line. In general, the solution approaches to solve the buffer allocation problem involve applying generative methods and evaluative methods in an iterative manner. In other words, generative methods and evaluative methods are combined in a closed loop configuration. In this configuration, an evaluative method is used to obtain the value of the objective function for a set of inputs. To search for an optimal solution, the value of the objective function is then communicated to the generative model.

Simulation, traditional Markov state models and decomposition methods are examples of evaluative methods. Various approaches can be used as generative methods. The Hooke-Jeeves method (Altiok and Stidham, 1983), knowledge-based methods (Vouros and Papadopoulos, 1998), dynamic-programmingbased methods (Chow, 1987, Jafari and Shanthikumar, 1989, Yamashita and Altiok, 1998, and Diamantidis and Papadopoulos 2004) and various heuristic procedures (Park, 1993, Papadopoulos and Vidalis, 2001, Tempelmeier, 2003, Nahas et al., 2006 and Sabuncuoglu et al., 2006) fall into this category.

Recently meta-heuristic approaches are widely used to solve the buffer allocation problem. Typical solution methods in this area include Tabu Search (Lutz et al., 1998 and Shi and Men, 2003), Simulated Annealing (Spinellis and Papadopoulus, 2000), Genetic Algorithms (Dolgui et al., 2002, 2007), and Ant Colony Optimization (Nourelfath et al., 2005 and Nahas et al., 2008).

In this study, an adaptive tabu search approach is proposed to solve the buffer allocation problem. Unlike the earlier studies employing tabu search to solve the buffer allocation problem in reliable lines (Lutz et al., 1999) or unreliable homogeneous production lines (Shi and Meni 2003), our study is the first one suggesting a novel adaptive search strategy of intensification and diversification for buffer allocation in unreliable and also non-homogeneous production lines. Besides suggesting a new strategy to tune the parameters of tabu search adaptively during the search, an experimental study is carried out to select an intelligent initial solution scheme among three alternatives so as to decrease the search effort to obtain the best solutions. The rest of this paper is organized as follows: The assumptions of the model and the buffer allocation problem are described in the next section. In section 3, the proposed solution approach is given in detail. Computational tests are presented in section 4. Finally, the findings of the study summarized and some future research directions are presented in the last section.

2. The buffer allocation problem

We consider a buffer allocation problem in a non-homogeneous unreliable production line. The features of this line can be listed as follows:

• Each part goes through all the machines in exactly the same order.

• There is an intermediate location for storage between each pair of machines.

• The machines in the line have different processing times.

• The machines are subject to breakdown, and the repair and failure rates of the machines are geometrically distributed.

• The first machine is never starved, i.e. input is always available, and the last machine is never blocked, i.e. there is always space to dispose of the output.

Assuming that there are K machines and K-1 buffers in a production line, the objective is to maximize the throughput rate of the production line, subject to buffer size constraints for each location. The mathematical model for the problem is formulated as follows:

Find 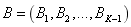so as to

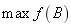                         （1）

subject to

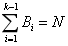                         （2）

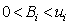                         （3）

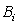 nonnegative integers 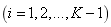               （4）

where N is a fixed nonnegative integer denoting the total buffer space available in the system, B represents a buffer vector, and f(B) represents the throughput rate of the production line. Constraint (3) shows upper (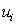) bounds for each buffer location. It should be noted that upper (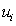) bounds for each buffer location are chosen such that their summation will be larger than N.

The buffer allocation problem is difficult for two reasons, as indicated by Chow (1987): (1) the lack of an algebraic relation between the throughput of the line and buffer sizes; and (2) the nature of combinatorial optimization inherent in the buffer design problem. In recent years, various search methods and meta-heuristics have been tried to effectively deal with the combinatorial nature of the buffer allocation problems. In this study, an Adaptive Tabu Search (ATS) algorithm is developed to solve the buffer allocation problem. The next section explains the specifics of our proposed solution approach in detail.

3. Proposed solution approach

To solve the buffer allocation problem under the assumptions explained in the previous section, the decomposition method is employed as an evaluative method, and an adaptive tabu search is proposed to obtain optimal buffer sizes. These methods are explained in detail in the following subsections.

3.1. Decomposition method

The decomposition method, proposed by Gershwin (1987), is based on the decomposition of the line into a set of K-1 two-machine lines L(i), for i=1,…,K-1. Line L(i) is composed of an upstream machine 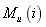, a downstream machine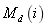, and buffer B(i) having the same capacity 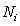, as buffer  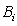in line L. The method is employed to determine the unknown parameters of each line L(i), i.e. the processing rates (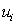), failure rates (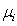) and repair rates (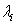) of upstream and downstream machines, so that the behavior of the material flow in buffer B(i) in line L(i) closely matches that of the flow in buffer Bi of original line L.

To determine the parameters of the two-machine lines, such that all the two-machine lines have the same throughput, and thus the conservation of flow is maintained, Dallery et al. (1988) develop the decomposition equations and an algorithm which is called DDX to solve these equations. Later, Burman (1995) extends this study to the non-homogeneous lines and develops an algorithm called accelerated-DDX (ADDX) algorithm. Due to its ability to obtain the throughput of a production line quite accurately and quickly, the ADDX algorithm is employed in this study as an evaluation method. For more details about the ADDX algorithm, the reader can refer to Burman (1995).

3.2. Adaptive tabu search (ATS)

Tabu Search (TS) is a meta-heuristic approach for solving combinatorial optimization problems. TS explicitly uses the history of the search, both to escape from local optima and to implement an explorative search. For more details about TS, the reader can refer to Glover and Laguna (1997).

The features of our adaptive TS algorithm for solving the buffer allocation problem are explained in this section.

Search space: All feasible solutions are considered as the search space.

Initialization: It should be noted that searching with a random initial solution is time consuming in reaching optimal solution. In this study, an experimental analysis has been carried out to decide on how to start the search with an efficient initial solution. Alternative initialization methods tested are as follows:

•Random initialization: Buffer sizes are randomly allocated to each machine.

•The ratio of failure to repair rate: Buffer sizes are allocated according to the ratio of failure to repair rate of each machine. More buffers are allocated to the machines having high ratio of failure to repair rate.

•Processing time: More buffers are allocated to the machines having long processing times.

The results of the experimental study comparing the performance of these three initialization schemes are given in Table 1. The experiments involve 4 distinct design points. 10 instances are created at each design point, totaling to 40 runs. In Table 1, K and N stand for the number of machines, and the total buffer capacity, respectively.

Table 1 shows the results of this comparative study. The comparison is based on both solution quality and the convergence rate. First, the methods are compared with respect to solution quality, in case the same solution quality is observed, to distinguish the best performing one, the convergence rate is used as a tie-breaking rule. As a result of this comparison, it is found that the performance of ratio of failure to repair rate method is better in 23 problem instances out of 40. Moreover, especially for the first problem set, its performance is quite remarkable. Hence, in testing the performance of the proposed adaptive tabu search algorithm, this method has been used as an initialization scheme.

Move representation: The moves are represented by [i, j], where i shows the location that a given amount of buffer is added and j shows the location that the same amount of buffer is subtracted. These locations can be any two locations. Moreover, the increment (decrement) of a buffer size is problemdependent. This value is set to 1 for small-sized problems, i.e. five and ten machine lines. For large-sized problems, i.e. twenty machine lines, this value is set to %1 of the total buffer size for each instance.

Neighborhood structure: The complete neighborhood of the current solution is created and evaluated. The move yielding the solution with the best objective value is considered for the next step. If the move is tabu, the best non-tabu move is selected.

Tabu Tenure: The tabu tenure is tuned adaptively according to the quality of the current solution and the frequency of the moves. Initially, the tabu tenure is set to its minimum value. The value of the tabu tenure for each move is determined by the following formula (Lü and Hao, 2010):

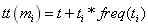                           （5）

The first part of the formula represents the effect of solution quality on the tabu tenure. Namely, if the selected move does not improve the objective function (i.e., throughput rate of the production line), the value of t is increased by 1. Likewise, if the selected move improves the objective function, the tabu tenure is decreased by 1. While making these changes, the tenure is not allowed to surpass its upper or lower bound values. The basic idea behind the second part of the formula is to penalize a move which repeats too often.

Intensification strategy: An intensification strategy is employed for large-sized, i.e. 20 machine problems. In the intensification strategy, if a solution found to be best so far remains to be best one for certain number of iterations, the increment (decrement) of moves is set to one. In this way, the areas of the search space that contain promising solutions are investigated more thoroughly.

Diversification strategy: We employ two mechanisms together to diversify the search, i.e., continuous diversification and restart diversification. In the continuous diversification phase, frequently performed moves are penalized. If the objective function does not change for a certain number of iterations, a random restart is applied. This way, the search is directed to an unvisited area of the search space.

Next section presents the results of experimental studies evaluating the performance of the proposed adaptive tabu search algorithm.

4. Computational Tests

In the computational experiments, we consider five, ten and twenty-machine lines (K = 5, 10, 20). For each of these levels, the total buffer size is set to five, ten and twenty times the number of machines in the line (N = 5, 10, 20). Hence, the computational study involves nine sets of problems and 10 instances are generated for each problem set. The processing rates of the machines are uniformly distributed in the range (5, 15), where the failure and repair rates are geometrically distributed in the range (1, 100).

The performance of the adaptive tabu search algorithm is compared to the simple tabu search algorithm over the generated instances. All algorithms are implemented in the C language. The execution is done on a computer having 3 Ghz Pentium (R) 4 CPU processor and 1 GB of RAM.

Table 2 presents the results of the computational runs. The performance of both algorithms is evaluated with respect to solution time (the CPU time in seconds) and solution quality (the throughput rate). For K = 5, the optimal solutions are obtained by employing the complete enumeration (CE). For K = 10, CE is terminated after 4 hours and the incumbent solution is used in comparisons. For K = 20, as CE cannot find good solutions in reasonable times, the results of the ATS algorithm is compared with the results of the simple TS. For each problem instance, both of the algorithms are executed for the same number of iterations depending on the problem size. The corresponding average CPU times are presented in the Table 2.

Table 1. The results of pilot experiments on the performance of initial algorithms

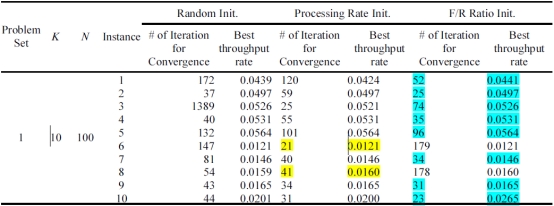
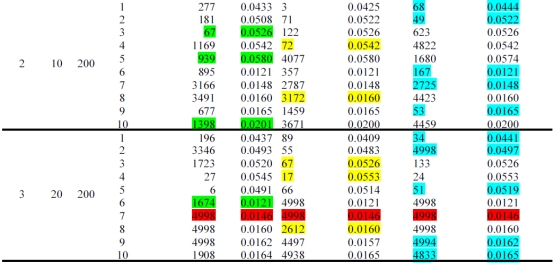
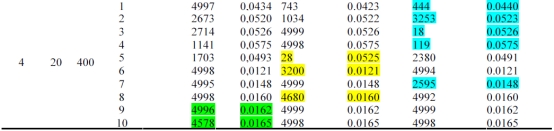
Table 2. Summarized results of comparative study

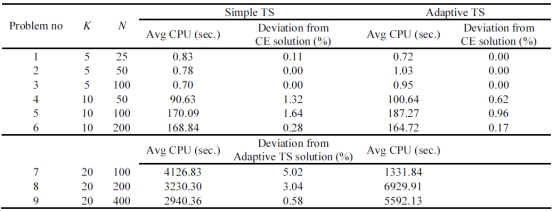
As seen in Table 2, for the problems with K = 5, ATS algorithm obtains the optimal solution for all instances with no significant increase in solution time, while the simple TS algorithm get stuck at local optima. For the problems with K = 10, ATS obtains better solutions than TS, and the solution times are quite similar for both algorithms. For larger-sized problems involving 20 machines, the solution quality of ATS is still better than the simple TS algorithm but this is achieved at the expense of increasing the solution time in the 8th and 9th problem sets. However, it should be noted that the solution time of both algorithms heavily depend on the convergence time of the ADDX algorithm. The convergence rate of the ADDX algorithm is set to 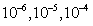 for each problem set, respectively throughout the experiments.

5. Conclusion

In this study an adaptive tabu search algorithm is proposed to solve buffer allocation problem in nonhomogeneous unreliable lines. The performance of the proposed algorithm is compared to the simple TS algorithm using randomly generated test problems. It should be noted that these test problems include both short and long production lines which have wide range of variability both in processing times and reliability parameters so that the efficiency of the proposed ATS can be tested thoroughly on a wide range of problem instances. The results of experimental studies are found to be quite encouraging. Namely, it has been observed that the proposed ATS algorithm always converges to the optimal solution for smallsized problems, i.e. five-machine lines. For medium-sized problems the efficiency of the proposed ATS algorithm increases when the total buffer size to be allocated in the system increases. The same behavior is observed for large-sized problems; namely the proposed ATS algorithm is superior to the simple TS algorithm in terms of solution quality.

In this study only the throughput maximization problem is considered. Especially if there is a budget constraint, solving the buffer allocation problem to minimize the total buffer size could be very valuable. So this study can be extended to minimize the total buffer size by using the proposed ATS algorithm. In this respect, the proposed ATS algorithm can be employed as a decision support tool to decide on the total buffer capacity to allocate to each machine in the line.