摘要:在设计生产线中,缓冲区配置问题是一个重要的研究课题,比如说在生产线里允许多少缓冲区存储和将其布置到哪。在本文中,缓冲区问题用来解决不可靠非均匀性的生产线,目标是将缓冲容量限制下生产线的吞吐量最大化,本文才用分解方法来评估生产线的吞吐量。适应性禁忌搜索方法用来对每一个工作站缓冲区尺寸最优化,优化方法的结果由计算试验得出。
关键词:缓冲区配置问题,生产线,适应性禁忌搜索,组合优化
1 引言
一个生产线包含一系列将生产线划分成阶段机器和缓冲区的排列组合,其性能取决于不同的处理时间和机器的可靠性参数,而在机器之间采用中间缓冲区能减少变化的影响。
缓冲区配置问题解决的是在生产线中找出能分配到缓冲区的最优化的缓冲区大小,总的来说,解决缓冲区配置问题的方法包括以迭代的方式应用生成和评估的方法。换言之,生成方法和评估方法在闭环配置下结合起来,在这种配置下,评估方法用来获得一套输入数据的目标函数值。为了搜索一个最优的方法,目标函数值和生成模型相连接。
模拟,传统的马尔可夫状态模型和分解方法是评估方法的例子,且各种方法可用于生成方法。胡克-吉福斯方法(阿尔特奥克和斯蒂德汉姆,1983),基于知识方法(Vouros和帕帕佐普洛斯),基于动态规划方法(周,1963,贾法里和Shanthikumar,1989,亚曼蒂迪斯和帕帕佐普洛斯,2004)以及各种启发程序(帕克,1993,帕帕佐普洛斯和威达里斯,2001,Tempelmeier,2003,Nahas et al.,2006,Sabuncuoglu et al., 2006)都属于这类。
在本文,适应性禁忌搜索用来解决缓冲区配置问题,不像早期研究采用禁忌搜索解决可靠生产线(Lutz et al., 1999)或者不可靠均匀生产线(Shi and Meni 2003)的缓冲区配置问题,我们研究针对于不可靠且非均匀生产线首次提出一个新颖的适应性搜索集约化和多样化方法。除了在搜索期间采用一个新的方法调整适应性搜索参数,为了减少得到最佳方案的搜索工作量,本文进行了一个实验性研究在三个可选择项中选择出一个智能初步解决方案。本文的其余部分组织如下:第二部分描述模型假设和缓冲区配置问题,第三部分详细给出了提出的解决办法,第四部分讲解了计算试验,最后一部分为概括的研究结果和一些未来探索方向。
2 缓冲区配置问题
我们考虑不可靠非均匀生产线中的缓冲区配置问题,生产线的特征如下所示:
·每一部分以同样的顺序通过所有的机器;
·在每一组机器之间设有供存储的中间工作站;
·生产线里的机器有不同的运行处理时间;
·机器有故障,同时机器的维修和故障率呈几何分布;
·第一个机器从不饥饿,比如输入总是有的,最后一个机器从不堵塞,比如总有空间来输出结果。
假设生产线有K个机器和K-1个缓冲区,目标是将生产线的输出率最大化,且受限于每个工作站缓冲区尺寸大小。问题的数学模型组成如下:
找到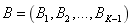 以此求
以此求
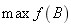 (1)
(1)
约束条件
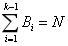 (2)
(2)
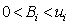 (3)
(3)
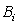 为正整数
为正整数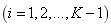 (4)
(4)
N是一个固定的正整数,表示系统中可达到的整个缓冲区容量;B表示缓冲区域;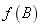 表示生产线的输出率;约束条件(3)表示每个工作站的上限(
表示生产线的输出率;约束条件(3)表示每个工作站的上限(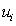 ),此处每个工作站选择的上限之和应大于N。
),此处每个工作站选择的上限之和应大于N。
正如周(1987年)指出,缓冲区配置问题因如下两个原因而困难:(1)在生产线输出和缓冲区尺寸之间缺少一个代数联系;(2)缓冲区设计问题中组合优化的特征。近年来,许多搜索方法和改进的启发式算法已被有效地解决缓冲区配置问题的组合特性,本文采用一种适应性探索禁忌方法来解决缓冲区配置问题,下一部分将详细解释我们提出的解决方法的细节。
3 提出的解决方法
为了解决前部分内容假设下的缓冲区配置问题,我们将分解方法视为一个评估方法,并且提出适应性探索方法来获得缓冲区大小,这些在下面部分有详尽的说明。
3.1 分解方法
1987年格什温提出的分解方法基于生产线分解成为一套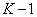 的两机器的生产线
的两机器的生产线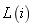 ,其中
,其中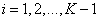 。生产线
。生产线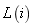 由一个上游机器
由一个上游机器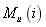 ,一个下游机器
,一个下游机器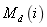 ,以及有着同样容量
,以及有着同样容量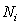 的缓冲区
的缓冲区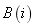 ,正如生产线
,正如生产线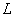 中的缓冲区
中的缓冲区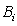 。这个方法是用来确定每个生产线
。这个方法是用来确定每个生产线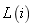 不知道的参数,比如上下游机器的处理率
不知道的参数,比如上下游机器的处理率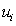 ,故障率
,故障率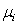 ,维修率
,维修率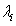 ,以便于生产线
,以便于生产线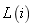 中缓冲区
中缓冲区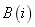 物质流的行为能与原生产线
物质流的行为能与原生产线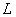 中缓冲区
中缓冲区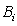 物质流行为紧密匹配。
物质流行为紧密匹配。
为了确定两台机器的生产线的参数,以便于所有两台机器的生产线有相同的吞吐量,进而能够维持流动,1988年Dallery et al.发明了一个分解方程和一个被叫做DDX的算法来解决这个等式。随后,1995年Burman将这个研究延伸到非均匀生产线,并发明了一个叫做加速DDX(ADDX)的算法。因为这个算法能够非常准确和迅速地获得一个生产线的吞吐量,ADDX算法在本文作为一个评估方法,如果想要对ADDX算法有更进一步的认识,读者可以参考Burman(1995)。
3.2 适应性禁忌搜索(ATS)
禁忌搜索是解决组合优化问题的一个启发式方法,TS明确地使用搜索历史,既避免忽略局部最优又完善一个探究性搜索,读者可以参考Glover and Laguna (1997)以此对TS进一步了解。
解决缓冲区配置问题的适应性禁忌搜索方法的特征在本部分解释如下。
搜索空间:所有可能的方法可以视为搜索空间。
初始化:应该指出用随机初始的方法去搜索达到一个最优的方法是费时的,本文进行了一个实验分析来决定怎样以一个有效的初始方法来进行搜索,选择性的初始方法测试如下:
·随机初始化:缓冲区大小随机分配到每个机器;
·故障维修率:缓冲区大小根据每个机器的故障维修率来分配,维修故障率高的机器分配的缓冲区多;
·处理时间:处理时间长的机器分配的缓冲区多。
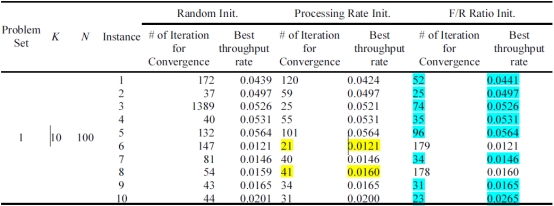
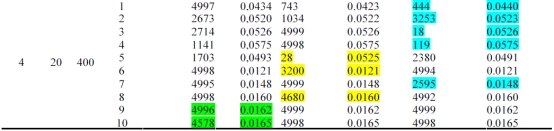
相对于三个初始方法的实验研究结果如表1所示。实验包含4个独特的设计要点,每个设计要点有10个实例,总共40个。在表1,K和N分别代表机器数量,整个缓冲区容量。
表1说明了对比研究的结果,对比是基于结果质量和收敛速度的。首先,关于不同的结果质量进行比较,以免相同的结果质量相比较,从而选出性能最好的一个,收敛速度被用作一个绳索断裂规则。对比结果发现40个实例中有23个的故障维修率性能更好。此外,特别是针对于第一个问题,结果非常有意义。因此,在对适应性禁忌搜索进行性能测试后,这个方法被用作一个初始方法。
移动代理:动作由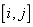 表示,i表示增加一定数量缓冲区的工作站,j表示减少一定数量缓冲区的工作站,这些工作站可以是任意两个工作站。此外,缓冲区大小的增量(递减)是相互独立的问题。对于小规模缓冲区问题动作设定为1,比如五个和十个机器生产线;对于大规模缓冲区问题,比如20个机器生产线,这个值设定为整个缓冲区规模大小的百分之一。
表示,i表示增加一定数量缓冲区的工作站,j表示减少一定数量缓冲区的工作站,这些工作站可以是任意两个工作站。此外,缓冲区大小的增量(递减)是相互独立的问题。对于小规模缓冲区问题动作设定为1,比如五个和十个机器生产线;对于大规模缓冲区问题,比如20个机器生产线,这个值设定为整个缓冲区规模大小的百分之一。
邻里结构:当前结果的所有近似解已产生并被评估,下一步考虑用最佳目标值解决方法的动作,如果这个动作时禁止的,那么最佳的允许动作就确定了。
禁忌占有期:禁忌占有期是根据目前解决方法的质量和动作的频率进行适应性地调整,初始时,禁忌占有期设定为最小值,每个动作的禁忌占有期值由下面的公式(Lü and Hao, 2010年)确定:
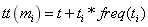 (5)
(5)
公式的第一部分代表方法质量在tabu tenure上的结果,也就是说,如果选择的动作不能使目标函数(例如生产线吞吐量)增加,t值则加1;同样的,如果选择的动作使目标函数增加,则t值减1,在这过程中,tenure不允许超过它的上下限值。公式第二部分意思是惩罚那些重复过多的行为。、
强化策略:强化策略用于大规模,比如20个机器的问题。在强化策略里,如果一个被认为最佳的方案在一定次数的迭代后仍保持为最佳方案,动作的增量(递减)设定为1。通过这种方法,包含可能的最佳方案的搜索空间的面积就彻底地被检查了。
多元化战略:我们将两种机制放在一起以使搜索多样化,例如持续多样化和重启多样化。在持续多样化阶段,经常进行的动作被惩罚。如果目标函数经过一定次数迭代后没有变化,随机的重启进行,这样搜索就指定到搜索空间未被访问的地方。
下一部分表示评估适应性禁忌探索方法实验研究的结果。
表1 关于初始算法性能的试点实验结果

4 计算试验
在计算试验中,我们假设有5,10,20个机器(K=5,10,20),对于每一个阶段,整个缓冲区大小设定为生产线机器数(N = 5, 10, 20)的5,10,20倍。因此,计算研究包含9个问题,每个问题有10个例子。机器的处理率通常分布于(5,15)故障维修率几何分布于(1,100)。
适应性禁忌搜索算法的结果和简单的搜索方法相比较,所有算法都通过C语言实现,电脑配置要求为3Ghz奔腾4处理器和1GB的内存。
表2为计算结果,两种算法的结果根据运行处理时间(每秒CPU处理时间)和方法质量(吞吐率)来评估。当K=5,最优方案通过完全列举(CE)来获得;当K=10,4小时后完全列举停止,现任的解决方案用于比较对照;当K=20,CE不能在合理的时间里找到最优方案,ATS算法的结果就和简单的TS结果进行比较。对于每一个实例,根据问题的大小,两种算法都要进行多次迭代,相应的CPU处理时间如表2所示。
表2 对比研究的结果汇总
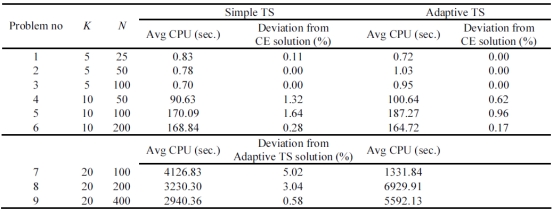
如表2所示,对于K=5,ATS算法在处理时间没有明显的增加下得到所有例子中的最优方案;对于K=10,ATS得到的方案比TS更好,两种算法的时间都十分相似;对于大规模问题包括K=20,ATS得到的方案仍然比TS好,但是在第八和第九个问题上要增加处理时间。然而,应该指出两种算法的处理时间都紧紧取决于ADDX算法的收敛时间,ADDX算法的收敛率在实验的各个阶段分别设定为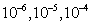 。
。
5 结论
本文所提出的适应性禁忌探索方法用于解决不可靠非均匀生产线中缓冲区配置问题,该算法通过随机测试问题与简单TS算法相比较,应该指出测试问题包含短的和长的生产线,这些生产线在处理时间和可靠度参数都在一定范围内具有变化性,从而ATS算法的效果能够通过一系列问题实例彻底的测试出。实验研究结果很有意义,结果发现对于小规模比如5个机器生产线,ATS算法总是收敛于最优方案;对于中等规模的,当分配于系统的整个缓冲区尺寸增加时,ATS算法的效率也增加;对于大规模的同样如此,在方案质量上,ATS算法比简单的TS算法优越。
本文只考虑了吞吐量最大化问题,特别是当预算有限制的时候,解决缓冲区配置问题来减少缓冲区尺寸将非常有价值,所以该研究可以通过使用ATS算法来使缓冲区尺寸最小化,在这方面,ATS算法可以作为将缓冲区容量分配生产线的一个决定性支持工具。



