VSS motion control for a laser-cutting machine☆

Ales\ Hace, Karel Jezernik*, Martin Terbuc

University of Maribor, Faculty of Electrical Engineering and Computer Sciences, Institute of Robotics, Smetanova ul. 17, SI-2000 Maribor, Slovenia

Received 18 October 1999; accepted 2 June 2000

Abstract

An advanced position-tracking control algorithm has been developed and applied to a CNC motion controller in a laser-cutting machine. The drive trains of the laser-cutting machine are composed of belt-drives. The elastic servomechanism can be described by a two-mass system interconnected by a spring. Owing to the presence of elasticity, friction and disturbances, the closed-loop performance using a conventional control approach is limited. Therefore, the motion control algorithm is derived using the variable system structure control theory. It is shown that the proposed control e!ectively suppresses the mechanical vibrations and ensures compensation of the system uncertainties. Thus, accurate position tracking is guaranteed. ( 2001 Elsevier Science ¸td. All rights reserved.)

Keywords: Position control; Drives; Servomechanisms; Vibrations; Variable structure control; Chattering; Disturbance rejection; Robust control1.

Introduction

For many industrial drives, the performance of motion control is of particular importance. Rapid dynamic behaviour and accurate position trajectory tracking are of the highest interest. Applications such as machine tools have to satisfy these high demands. Rapid movement with high accuracy at high speed is demanded for laser cutting machines too. This paper describes motion control algorithm for a low-cost laser-cutting machine that has been built on the base of a planar Cartesian table with two degrees-of-freedom (Fig. 1). The drive trains of the laser-cutting machine are composed of belt-drives with a timing belt. The use of timing belts in the drive system is attractive because of their high speed, high efficiency, long travel lengths and low-cost (Haus, 1996). On the other hand, they yield more uncertain dynamics and a higher transmission error ( Kagotani, Koyama & Ueda, 1993). Consequently, belt-drives suffer from lower repeatability and accuracy. Moreover, the belt-drive dynamics include more resonance frequencies, which are a destabilising factor in a feedback control (Moon, 1997). Therefore, a conventional control approach like PI, PD or PID control fails to achieve acceptable performance. Plant parameter variations, uncertain dynamics and load torque disturbances, as well as mechanical vibrations, are factors that have to be addressed to guarantee robust system stability and the high performance of the system. An advanced robust motion control scheme is introduced in this paper, which deals with the issues related to motion control of the drives with timing belts. The control scheme is developed on the basis of the motion control algorithm introduced by Jezernik, Curk and Harnik (1994). It possesses robust properties against the disturbances that are associated with a nominal plant model, as it has been developed with the use of the variable structure system (VSS) theory (Utkin, 1992). The crucial part of the control scheme is the asymptotic disturbance estimator. However, as shown in this paper, it fails to stabilise resonant belt dynamics, since it was developed for a rigid robot mechanism. Therefore, this paper introduces an improved motion control scheme, which suppresses the vibrations that would arise due to the non-rigid, elastic drive. Consequently, a rapid response with low position tracking error is guaranteed.

The paper is set out as follows. The laser-cutting machine is presented and the control plant model of the machine drives is developed in Section 2. In Section 3, the VSS control regarding the elastic servomechanism is discussed and the derivation of the motion control scheme is described. Section 4 presents the experimental results and a follow-up discussion. The paper is summarized and concluded in Section 5.

2. The control plant

2.1. The machine description

The laser-cutting machine consists of the XY horizontal table and a laser system (Fig. 1). The fundamental components of the laser system are:

● the power supply unit, which is placed off the table and thus is not considered in the motion control design;

● the laser-beam source, which generates the laser beam (the laser-generator);

●the laser-head, which directs the laser beam onto the desired position in the cutting plane.

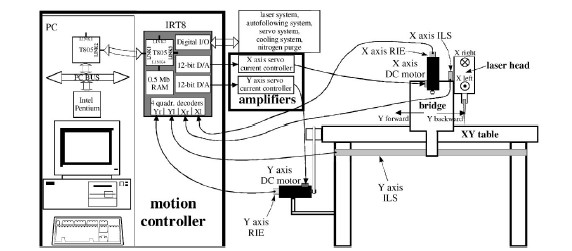
Fig. 1. The machine and the controller hardware.

The table has to move and position the laser head in a horizontal plane. This is achieved by the means of a drive system with two independent motion axes. They provide movement along the Cartesians' XY axes of 2 and 1m, respectively. The X-drive provides the motion of the laser-head in X-direction. The drive and the laser-head as well as the laser-generator are placed on the bridge to ensure a high-quality optical path for the laser-beam. The movement of the bridge along the Y-axis is provided by the Y-drive. The laser-head represents the X-drive load, while the Y-drive is loaded by the bridge, which carries the complete X-drive system, the laser-head, and the laser-generator. The loads slide over the frictionless slide surface.

The positioning system consists of the motion controller, the amplifiers, the DC-motors and the drive trains. The X-drive train is composed of a gearbox and a belt-drive (Fig. 2). The gearbox reduces the motor speed, while the belt-drive converts rotary motion into linear motion. The belt-drive consists of a timing belt and of two pulleys: a driving pulley and a driven pulley that stretch the belt. The Y-drive train is more complex. The heavy bridge is driven by two parallel belt-drives; each bridge-side is connected to one of the belt-drives. The driving pulleys of the belt-drives are linked to the driving axis, which is driven via the additional belt-drive and the gearbox is used to reduce the speed of the motor.

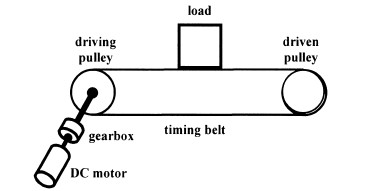
Fig. 2. The drive.

2.2. Assumptions

The machine drives represent a complex non-linear distributed parameter system. The high-order system possesses several resonant frequencies that can be observed by the drives' step response (see Section 4). From a control design perspective, difficulties arise from mechanical vibrations that are met in the desired control bandwidth (~10 Hz). On the other hand, the design objective is to have a high-performance control system while simultaneously reducing the complexity of the controller. Therefore, a simple mathematical model would only consider the first-order resonance and neglect high-order dynamics. In other words, the design model of the control plant will closely match the frequency response of the real system up to the first resonance. Next, the controller should be adequately designed to cope with the higher-order resonance in such a way that the resonance peaks drop significantly to maintain the system stability. Thus, according to the signal analysis and the drives' features, the following assumptions could be made:

●the DC-servos operating in the current control mode ensure a high-dynamic torque response on the motor axis with a negligible time constant;

●the small backlash in the gearboxes and the backlash of the belt-drives due to the applied pre-tension of the timing belts is negligible;

●a rigid link between a motor shaft and a driving pulley of the belt-drive could be adopted;

●the inertia of the belt-drives' driven pulleys is negligible in comparison to other components of the drive system.

Using the assumptions above, dynamic modeling could be reduced to a two-mass model of the belt-drives that only includes the first resonance. In the control design, the uncertain positioning of the load due to the low repeatability and accuracy of the belt-drive has to be considered as well.

Note, that no attention is paid to the coupled dynamics of the Y-drive due to the parallel driving, thus, the double belt-drive is considered as an equivalent single belt-drive.

2.3. The belt-drive model

The belt-drives could be modelled as a multi-mass system using modal analysis. In the belt-drive model with concentrated parameters, linear, massless springs characterize the elasticity of the belt. According to the assumptions above, a two-mass model can be obtained. The driving-pulley, motor shaft and the speed reducer are considered as the concentrated inertia of the driving actuator. The driven-pulley and the load are concentrated in the load mass. The inertia and the mass are linked by a spring. Friction present in the motor bearings, the gearbox, the belt-drive, and non-modelled higher-order dynamics are considered as an unknown disturbance that affects the driving side as well as the load side. The mechanical model of the two-mass system and its block scheme are shown in Figs. 3 and 4, respectively.

The belt-stretch occurs due to the inherent elasticity of the timing belts. However, according to a vibration analysis of belt-drives (Abrate, 1992), the obtained model could be rearranged. Assume the unit transmission constant (L=1). Then, the control plant model is presented by Fig. 5. The control plant consists of two parts connected in a cascaded structure. The first part is described by poorly damped dynamics due to the elastic belt. The second part consists of the load-side dynamics. The belt-stretch τ

forced by the applied torque q. The dynamics are described by Eq. (1)

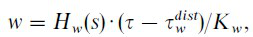
（1）

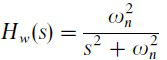where Hw(s) denotes the belt-stretch dynamics transfer function，

（2）

and 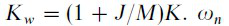                              is the natural resonant frequency

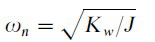
（3）

and 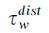          is hte disturbance that affects the belt. The load-side dynamics are 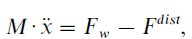                                                              （4）

                (4)

where Fw denotes the force, which drives the load

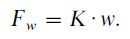
（5）

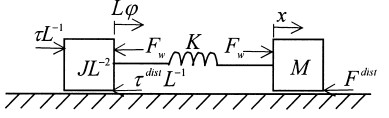
Fig. 3. The mechanical model of the elastic drive. M is the load side mass; J the driving side inertia; K the spring stiffness; 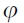 the motor shaft angular position; x the load position; w the belt-stretch; τ the motor shaft torque;  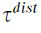the driving side disturbance torque; 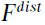the load side disturbance force;  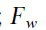the spring force and ¸ 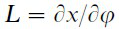the transmission constant.

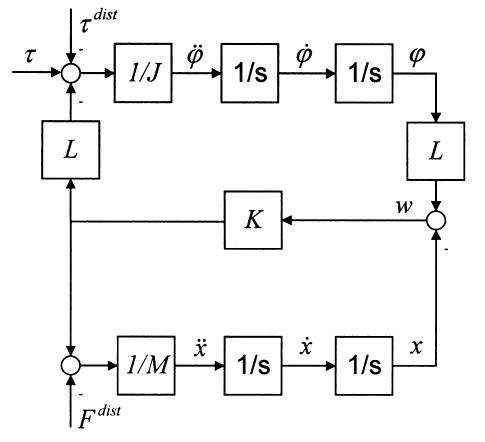
Fig. 4. The block scheme of the mechanical model: symbol are as

explained in Fig. 3.

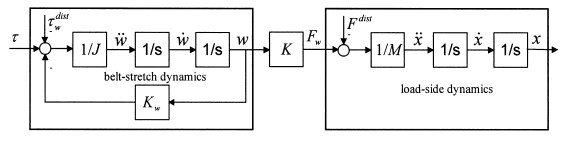
Fig. 5. The block scheme of the control plant.

3. The motion control algorithm

The erroneous control model with structured and unstructured uncertainties demands a robust control law. VSS control ensures robust stability for the systems with a non-accurate model, namely, it has been proven in the VSS theory that the closed-loop behavior is determined by selection of a sliding manifold. The goal of the VSS control design is to find a control input so that the motion of the system states is restricted to the sliding manifold. If the system states are restricted to the sliding manifold then the sliding mode occurs. The conventional approach utilises discontinuous switching control to guarantee a sliding motion in the sliding mode. The sliding motion is governed by the reduced order system, which is not affected by system uncertainties. Consequently, the sliding motion is insensitive to disturbance and parameter variations (Utkin, 1992).

The essential part of VSS control is its discontinuous control action. In the control of electrical motor drives power switching is normal. In this case, the conventional continuous-time/discontinuous VSS control approach can be successfully applied. However, in many control applications the discontinuous VSS control fails, and chattering arises (S[abanovicH, Jezernik, & Wada, 1996; Young, Utkin & OG zguK ner, 1999). Chattering is an undesirable phenomenon in the control of mechanical systems, since the demanded performance cannot be achieved, or even worse―mechanical parts of the servo system can be destroyed. The main causes of the chattering are neglected high-order control plant dynamics, actuator dynamics, sensor noise, and computer controlled discrete-time implementation in sampled-data systems. Since the main purpose of VSS control is to reject disturbances and to desensitise the system against unknown parametric perturbations, the need to evoke discontinuous feedback control vanishes if the disturbance is sufficiently compensated for, e.g. by the use of a disturbance estimator (Jezernik et al., 1994; Kawamura, Itoh & Sakamoto, 1994). Jezernik has developed a control algorithm for a rigid robot mechanism by combining conventional VSS theory and the disturbance estimation approach. However, the rigid body assumption, which neglects the presence of distributed or concentrated elasticity, can make that control input frequencies of the switcher excite neglected resonant modes. Furthermore, in discrete-time systems discontinuous control fails to ensure the sliding mode and has to be replaced by continuous control (Young et al., 1999). Avoiding discontinuous-feedback control issues associated with unmodelled dynamics and related chattering are no longer critical. Chattering becomes a non-issue.

In plants where control actuators have limited bandwidth there are two possibilities: actuator bandwidth is outside the required closed-loop bandwidth, or, the desired closed-loop bandwidth is beyond the actuator bandwidth. In the fist case, the actuator dynamics are to be considered as the non-modelled dynamics. Consequently, the sliding mode using discontinuous VSS control cannot occur, because the control plant input is continuous. Therefore, the disturbance estimation approach is preferred rather than VSS disturbance rejection. In the second case, the actuator dynamics are to be lumped together with the plant. The matching conditions (Draz\enovicH, 1969) for disturbance rejection and insensitivity to parameter variations in the sliding mode are violated. This results from having dominant dynamics inserted between the physical input to the plant and the controller output. When unmatched disturbances exist the VSS control cannot guarantee the invariant sliding motion. This restriction may be relaxed by introducing a high-order sliding mode control in which the sliding manifold is chosen so that the associated transfer function has a relative degree larger than one (Fridman

& Levant, 1996). Such a control scheme has been used in a number of recently developed VSS control designs, e.g. in Bartolini, Ferrara and Usai (1998). In the latter, the second-order sliding mode control is invoked to create a dynamical controller that eliminates the chattering problem by passing discontinuous control action onto a derivative of the control input.

The system to be controlled is given by Eqs. (1) ―(5) and the system output is the load position. The control objective is the position trajectory tracking. The control algorithm that is proposed in this paper has been developed following the idea of the VSS motion control presented by Jezernik. Since the elastic belt-drive behaves as a low bandwidth actuator, the conventional VSS control algorithm failed to achieve the prescribed control objective. Thus, the robust position trajectory tracking control algorithm presented in the paper has been derived using second-order sliding mode control. In order to eliminate the chattering problem and preserve robustness, the control algorithm uses the continuous control law. Following the VSS disturbance estimation approach, it will be shown that the disturbance estimation feature of the proposed motion control algorithm is similar to the control approach of Jezernik (Jezernik et al., 1994). Additionally, the proposed control algorithm considers the actuator dynamics in order to reshape the poorly damped actuator bandwidth. Consequently, the proposed motion controller consists of a robust position-tracking controller in the outer loop and a vibration controller in the inner loop (Fig. 6). This section is organized as follows. Section 3.1 presents the proposed VSS control design. Section 3.2 describes the derivation of the robust position controller.Section 3.3 provides a description of the vibration controller. Finally, the proposed

control scheme is described in Section 3.4.