激光切割机的传动控制可变结构系统

艾力斯•霍斯，卡瑞尔•诘责尼克，马丁•特布

马里博尔大学机器人学学院电气工程系和计算机科学系

截稿于1999年10月18日，出版与2000年6月2日.

内容摘要﹕

一个先进的位置跟踪控制算法被开发和应用于数控激光切割机的运动控制器。激光切割机的驱动机构是由带传动机构组成的。弹性伺服机构可以把它看成是一个弹簧连接的双量机构。由于存在弹性,摩擦和障碍,闭环性能使用传统的控制方法是有限的。因此, 可以利用可变系统结构控制理论从推导出运动控制算法。算例分析表明文中有效控制抑制机械振动和保证系统补偿的不确定性。因此,确保准确的位置跟踪。(2001爱思唯尔科学¸td。版权所有。)

简介：

对许多工业驱动器，运动控制的性能极其重要。快速动态行为和准确位置轨迹跟踪是最高的利益。如应用在机床必须满足这些高要求。激光切割机也是，它要求快速运动且高准确度。这篇论文讲述了一种低成本的激光切割机－建立在有两个自由度的二维笛卡尔表基础上的运动控制算法(图1)。激光切割机的驱动机构由有一个正时带的带传动组成的。驱动系统中的正时带具有吸引力是因为它具有高速度、高效、远距离行进和低成本的特性(霍斯,1996) 。另一方面,他们产生较多的不确定的动态和更高的传动误差(Kagotani,小山和建筑师,1993)。因此,传动带遭受较低的重复性和准确性。此外,带传动动力学包括很多的谐振频率，即反馈控制中的不稳定因素。因此,传统的控制方法像比例积分控制、比例微分控制或比例积分微分控制不能实现可接受的性能。设备参数的变化、不确定的动态和负载转矩的干扰,以及机械振动是必能保证系统的强稳定性和系统的高性能的因素。在这片论文中讲述了一种先进的稳定的运动控制方案,内容涉及到正时带驱动的运动控制。控制方案是在运动控制算法的基础上由Jezernik,Curk和Harnik1994年研制出的。用变结构系统(VSS)理论使其得到了强健的抵御与一个名义上的对象模型有关的干扰的性能。渐近线的扰动估计量是控制方案的关键的部分。 然而,如本文所示, 因为是为刚性机器人机制而研制的故不是稳定谐振带动力学。因此,介绍了一种改进后的会出现非刚性、弹性传动的振动运动控制方案。因此,保证其低位置跟踪误差的快速反应。

本文提出如下。激光切割机的陈述和控制系统模型机械传动在文章的第二节。在第三节,深入探讨,对于关于系统弹性伺服机构 可变结构系统控制并对运动的起源控制方案进行了介绍。第四节是实验结果和后续讨论。摘要在第五部分总结和归纳了。

2.模型控制

2.1 .机床的描述

激光切割机包括XY工作台和激光系统（如图1）。激光系统的基本组成部分﹕

●由于没有考虑运动控制设计，因此电源设备被放置在后台﹔

●激光束来源即产生激光束(激光器) ﹔

●激光头－引导激光到理想的剖切面上所需的地点。

必须移坐标轴且与放置激光头在水平面里。通过用两个独立的运动轴的驱动系统来实现这样的水平面。他们提供沿卡迪尔XY轴和Z轴移动。X轴传动使激光头沿着X轴方向的运动。 驱动机构﹑激光头以及激光器放置在桥接器上,可以确保激光束有一条高品质的光路径。Y轴运动是由Y传动提供的。激光头代表X驱动的负荷, 它负载了全部X驱动系统，包括激光头和激光器，而Y驱动由电机来负载。 这些负载在无阻力的滑动面滑过。

定位系统由运动控制器,放大器,直流电机与驱动系统。X驱动机构是由一变速箱以及带传动(图2)。 当带传动由旋转运动转化为线性运动变速箱降低了电机的转速。带传动由正时带和两个滑轮组成﹕让皮带运动的主动轮和从动轮。而Y驱动机构更为复杂。沉重的桥接器由两条平行传动带驱动;每个桥面都连接到其中一个传动带上。传动机构通过减少马达的速度的传动带驱动和变速箱来带动的主动轮与传动系联系。

2 .2  假设

这台机器驱动代表一个复杂的非线性分布参数系统。高阶系统拥有多项的能被驱动器的阶跃响应观测到的共振频率(见第4部分)。根据控制设计观点,困难产生于在所要控制带宽(~ 10赫兹)出现的机械振动。另一方面,设计的目的是得到一个高性能控制系统的同时又能降低控制器复杂性。因此,一个简单的数学模型将只考虑它的一阶共振,而忽视高阶动态。换句话说,控制设备的设计模型将密切配合真正系统频率响应直到第一阶共振。其次,控制器设计应充分地应对多谐振峰值的大幅下降直到保持系统的稳定性的情况下的高阶共振。因此,根据信号分析与驱动装置的特点,假设制定为如下:

●在电流控制方式里直流伺服系统的运作确保在电机轴上有一个忽略的时间常数的高动态扭矩。

●变速箱里的小间隙和取决于应用拉伸的正时带的带传动机构的间隙是可以忽略不计的。

●电机轴和传动机构中的主动轮的刚性关联是可采用的。

●相对其他传动系统中的部件从动带轮的惯性是可以忽略不计的。

用以上假设,动态模型将缩减至一个有两个传动轮的只包含一阶共振的传动机构。在控制设计,由于传动机构的可重复性和准确性都比较低，负载的不确定的位置必须加以考量。

没有注意到的耦合的动力学Y轴传动由于平行传动,因此,双履带传动可看成同级别的单履带传动。

2.3 带传动模型

可用一个多质子系统仿制带传动机构采用模态分析。 在带传动机构模型有着集中参数的、线性的、无质量的弹簧表示履带的弹性。根据以上的假设条件,可以得到轮-车架系统模型。主动轮、电机轴和减速机都被看作是驱动执行机构的集中惯量。从动轮及负载主要集中在负荷质量上。惯量和负荷由弹簧联系的。电机轴承、齿轮箱、传动机构以及非模型的高阶动态里的摩擦力都被看作是一个影响着传动方面还有负载方面的不为人知的干扰。轮-车架系统的力学模型系统及其方案分别显示在图3和图4。

皮带的延展由于正时带的固有弹性。但是,根据传动机构的振动分析,所得到的模型能够调整。假设单位传送值为常数(L= 1)。然后,控制对象模型如图5。控制设备包括两个由一个串级结构连接的部分。第一部分用取决于天性履带的阻尼动力学差来描述。第二部分包括负载部分动力学。带延伸τ被迫通过应用扭矩q。描述了动力式（1。

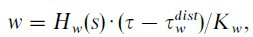
（1）

Hw(s)表示带张力动力学的传递函数

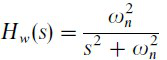
（2）

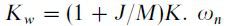是自然共振频率

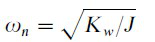（3）

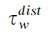是带的阻力。负载动力公式是

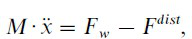                                                             （4）

Fw传动负载的力

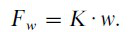
（5）

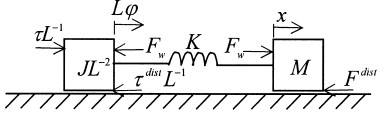
图3是弹性驱动力学的模型。M是负荷端质量;J是动测惯量﹔K是弹簧刚度﹔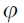是机轴角位置﹔x负负载位置﹔w是带张力﹔τ是干扰力矩; 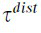是传动干扰力矩﹔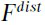是负载干扰力矩﹔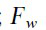是弹簧干扰力矩﹔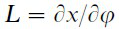是传递常数。

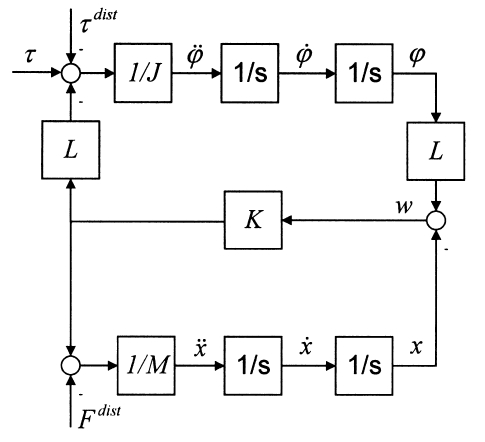
图4 力学模型方框图:所提到的字母解释是一样的。

图5是控制装置的方框图

3.运动控制算法

由于错误的不确定的结构化和非结构化的的控制模型的要求,提出了一种鲁棒控制律。传动控制变可变结构系统保证了不确定模型系统的鲁棒稳定性,即它已被证明在传动控制变可变结构系统理论,就是闭合回路决定于移动方式的选择。传动控制变可变结构系统的目标控制设计是找到一个控制输入,这样的运动系统的状态仅局限于滑动方式。如果系统的状态是局限于滑动方式然后一移动的模型的出现。传统的方法利用不连续的切换控制保证了滑动运动在滑模面里。滑模面是由不受系统中的不确定性影响的降阶系统控制的。因此,滑模面不受扰动和参数变化的影响(Utkin,1992年)。

传动控制变可变结构系统控制的主要部分是它的不连续控制作用。控制电机驱动电源转换装置是正常的。在这种情况下,传统的连续时间/不连续传动控制变可变结构系统控制方法可以得到了成功的应用。然而,在很多不连续传动控制变可变结构系统的控制应用程序都失败了还发生震动。振动在力学系统里是一个不良的现象，因为所要求的操作不能实现，更糟糕的是伺服系统的机械零件都有可能被弄毁。震动的主要原因是忽略高阶控制装置动力学、气动执行机构动力学、传感器噪声,还有在数据采样系统里的计算机离散时间的实施。因为传动控制变可变结构系统控制的主要目的就是抵制干扰及系统的未知干扰参数，如果扰动具有足够的补偿就有必要使不连续的反馈控制消失,例如通过使用干扰估计。诘责尼克已经开发了一种实现机械刚性原理通过结合常规传动控制变可变结构系统控制理论及干扰估计的方法的控制算法。然而,忽视了分散或者集中应力的存在的刚体假设会使转换装置的控制输入频率引起与忽略的模型共振。此外,在离散系统里的不连续控制不能保证滑模面,取而代之的是采用连续控制。为避免与为建模动力学和震动有关的不连续反馈控制相关的问题不再是至关重要的。震动是一个不重要的问题。

设备里控制执行机构的装置，它有两种可能的有限的带宽:执行机构带宽超出所要求的闭合回路的带宽,或者,想要的闭合回路带宽超出了执行机构的带宽。在第一种情况里,制动器动力学将会被认为是非模型动力学。因此,该滑模控制采用不连续传动控制变可变结构系统控制不能实行,因为控制设备输入是连续的。因此,干扰估计方法者优先考虑,而不是传动控制变可变结构系统控制抑制扰动。在第二种情况下,驱动器动力学是与设备合并在一起的。在滑膜里与抑制扰动和灵敏度的参数的变化相一致的情况是违反的。因为装置具有的主导动力学之间插入物理输入和控制器的输出。当为抵消的干扰存在于传动控制变可变结构系统不能保证不变滑模面。这一限制可以轻松通过引入高阶滑模控制就是多种滑模的选择,以便相关的传递函数有一个相对阶数大于一。这样的一种控制方案已被用于很多最近发展起来的传动控制变可变结构系统控制设计里，如在巴图里尼、费拉拉和埃塞里。后来,二阶滑模控制被调用来创建一个动态控制器通过在一种派生的控制输入上短暂的不连续控制作用消除了抖振问题。

该系统将被给定的方程式控制。图(1)-(5)和系统输出是负载的位置。控制目标是位置的轨迹跟踪。本文提出控制算法根据诘责尼克提出的传动控制变可变结构系统控制运动控制理论被发现了。因为弹性传动机构和制动器的带宽很相像所以传统的传动控制变可变结构系统控制算法未能实现规定的控制目标。因此,本文中所出现的系统的鲁棒轨迹跟踪控制算法已经派生的用到在二阶滑模控制里。为了消除抖振问题和保存的鲁棒性,控制算法采用连续控制方法。根据传动控制变可变结构系统控制干扰的估计方法,将会发现所提出的运动控制计算的干扰估计特性与诘责尼克的控制算法相似。此外,所提出的控制算法考虑了执行机构的动力,以期重塑这些低度阻尼致动器的带宽。因此,本文提出的运动控制器由一种在外回路的鲁棒位置追踪控制器和在内回路的振动控制器组成(图6)。这部分被安排在如下章节里。3.1节介绍了提出的传动控制变可变结构系统控制设计。第3.2节描述的鲁棒性位置控制器的起源。第3.3节描述的是振动控制器。最后,所提到的控制方案在3.4节里出现。