The superscript p is used to denote the time dependence of T, and the time derivative is expressed in terms of the difference in temperatures associated with the new (p + 1) and the previous (p) time steps.

Eqs. (3) and (12) are solved using an explicit FDM for the chill and casting by

which can be rearranged as,

where Fo is a finite difference form of the Fourier number,

Eq. (17) is explicit because the unknown nodal temperatures for the new time are determined exclusively by the known nodal temperatures at the previous time. Hence, calculation of the unknown temperatures is straightforward. Since the temperature of each interior node is known at t = 0 (p = 0) from the prescribed initial conditions, the calculation begins at t = Dt (p = 1), where Eq. (17) is applied to each interior node to determine its temperature. With the temperatures known for t = Dt, the appropriate finite difference equation is then applied at each node to find the temperatures at t = 2Dt (p = 2). In this way, the transient temperature distribution is obtained by marching out in time, using intervals of Dt.

The accuracy of the finite difference solution may be improved by decreasing the values of Dx and Dt. Of course, the number of interior nodal points that must be considered increases with smaller mesh interval width Dx, and the number of time intervals required to carry the solution to a prescribed final time increases with decreasing time interval Dt. Hence, the computation time increases with finer resolutions Dx and Dt.

Eq. (17) must be written for both the casting and the chill elements, separately. For convergence of the calculation, the element size and time step are to be chosen under consideration of

The terms in Eq. (18), Dx and Dt, refer to the space and time increments used in the calculations .In this work, the differential elements are selected as Dx = 0.5 mm and, consequently , Dt 6 0.0017 s for both the casting and the chill, complying with Fo 6 0.5.

3.2. Boundary conditions and solution

In the present work, the initial temperature and boundary conditions are chosen as follows:

where the temperatures used for the boundary conditions, Ti, Tm and Tm, are obtained during the experiments, measured in two symmetrically located thermocouples in the chill and casting at L = 75 mm from the metal–chill interface.

The first temperatures recorded by the thermocouples placed, symmetrically, 75 mm from the metal casting–chill interface were used as initial temperatures, Eq. (20), at t = 0 in the casting and chill, respectively. The temperatures from these thermocouples were also used as boundary conditions

at later times in the finite difference calculations, Eqs. (21) and (22), respectively. The boundary conditions at the interface were obtained by assuming uniform surface temperatures over the surfaces of the casting and chill. The temperatures are read from the thermocouples every 0.5 s, defined as the time period of measurements.

The calculated temperatures, 5 mm from the interface in the casting and the chill, respectively,were compared with the measured temperatures obtained at the same points. For this purpose, the actual location of the thermocouple between two adjacent nodes was determined, and the temperature was interpolated linearly between them. The supposed surface temperatures at the casting and chill interface were then modified, and the finite difference calculation for the previous 0.5 s time interval was repeated. The accuracy of the numerical simulations has been set to agree by ±0.1 K with the measured temperatures for the points at the 5 mm symmetrical distances from the interface in the casting and the chill.

In this way, a reliable temperature field has been determined that gave the surface temperatures of the casting and the chill at the interface within the selected accuracy of ±0.1 K.

4. Results and discussions

Temperatures were experimentally measured in six locations: in the chill and casting, symmetrically at 5 mm, 37.5 mm and 75 mm from the casting–chill interface, respectively. They are shown in Fig. 4 together with the calculated temperatures following from the numerical simulation in the chill (TM) and casting (TC) interface of the eutectic Al–Si casting and the water cooled steel chill. Fig. 5 shows the same data for the eutectic Al–Si casting and the water cooled copper chill. The variations of the temperature field in the course of the experiments can be followed for both the steel and copper chill, in Figs. 4 and 5, and are in good agreement with the thermophysical laws.

In order to check the precision attained by the FDM, the calculated temperatures in the casting at a point 37.5 mm from the casting–chill interface were compared with the temperatures measured at this point in a period of 0.5 s.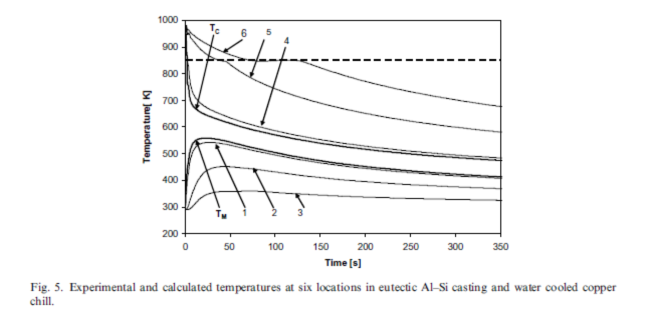  

The measured and calculated temperatures in the mid-points (37.5 mm) from the interface in the chill and casting are monitored to control the reliability of the correlation between the measurements and the numerical calculation. In the chill mid-point, where only heat conduction governs, the agreement of the measurements and calculations is excellent, with less than 1–2 K difference, considering the accuracy limits of the thermocouples employed.

On the other hand, the phase changing events in the casting complicate the calculation of temperatures. In the literature, temperature differences < ±20 K between the measurements and numerical calculation in the casting are accepted [3]. In the present study, good agreement between the measurements and numerical calculation has been attained. Figs. 6 and 7 show the calculated and measured temperatures in the middle of the eutectic Al–Si casting over the water cooled steel and copper chills, respectively. The right ordinates in these figures indicate the temperature difference between the calculation and measurement. In the casting mid-point, the calculated and measured temperatures have overlapped over the solidus time, and in the liquidus time, the temperature difference has not exceeded 16 K and 14 K with the steel and copper chills, respectively. Figs. 6 and 7 demonstrate clearly the high reliability and accuracy of our calculations for determination of the time varying temperature fields in the chill and

casting.

4.1. Cooling curves and heat transfer coefficient

After the determination of the temperature field, the heat transfer between the casting and chill has been calculated with the help of Eq. (2) and is shown in Fig. 8 for the copper and steel chills.Then, the IHTC has been evaluated with the help of Eq. (1). The time dependent variation of the IHTC is shown in Fig. 9, from the initial moment of the casting process until a quasi-stationary situation is reached, and can be distinguished in mainly three stages.

4.1.1. First stage

Liquid is poured in the mold. In the very early 10–20 s, a sufficiently high liquid column is not yet formed so that this phase should be completely ignored. In the first stage, while the metal is completely liquid and has perfect contact with the chill surface, the heat transfer coefficient reaches its maximum value of about 19 kW/m2 K for the copper chill and 6.5 kW/m2 K for the steel chill. Our calculated IHTC values are very similar to those in the literature for

solidifying aluminum alloys in copper and steel molds [10,26,30,31]. No skin formation of solid metal on the chill surface will occur due to the turbulences during the molten metal pouring phase into the mold. When pouring is stopped, the turbulences die out. A thin stable skin of solidified metal is formed on the chill because the chill extracts heat from the molten metal.The interface is pressed against the chill by the hydrostatic pressure of the liquid metal. Then,the IHTC for the copper chill decreased sharply for a short time. The first stage lasts only up to 30 s because of the high heat conductance of the copper chill. However, it lasts up to 120 s for the steel chill of lower heat conductance, in which time the IHTC decreased gradually with time. The effect of hydrostatic pressure decreases with the increasing of the solid skin thickness. In the first stage, some parameters, such as the wettability of the liquid on the chill surface, the

amount of melt super heat, surface roughness, mold temperature, pouring momentum of melt,thermal conductivity of chill, hydrostatic pressure and turbulence of melt, affect the heat transfer coefficient.

4.1.2. Second stage

After formation of an adequate solid metal on the chill surface, the perfect contact between the chill and the solidified casting no longer exists because of contraction of the solidified casting. In addition, the thermal conductivity of the liquid is much higher than that of the solid. However,the decreasing of the IHTC on the copper chill proceeds continuously due to the remaining intimate contact and its high conductivity until solidification is completed at 135 s. Fig. 9 shows the IHTC on the steel chill in the second stage tended to remain at constant values, approximately 6 kW/m2 K during solidification of the casting, until 310 s because the heat extraction rate by the steel chill is not as high as that of the copper chill and the temperature differences between

the solid metal and chill surfaces (TC _ TM) decrease in time. It can be seen in Figs. 4 and 5 for the steel and copper chills, respectively. Solidification orientation, thermal conductivity and surface roughness of the chill are the most important parameters of the heat transfer coefficient in this stage.

4.1.3. Third stage

After solidification of the metal in the mold on the copper chill is completed, the IHTC continues to decrease to lower values due to the high conductivity of copper. On the other hand, the IHTC on the steel chill remains at constant values. The effect of the solidified casting contraction might be balanced by the thermal expansion of the steel chill that might produced a constant contact pressure between the casting and chill surfaces.

5. Conclusions

Our calculated results have shown that the applied model for determination of the metal casting–chill IHTC in one dimensional heat flow is achieved successfully, and the following conclusions can be summarized as follows:

1. A satisfactory FDM to evaluate the IHTC at the Al–Si eutectic metal casting at both the copper and steel chill interfaces has been achieved for one dimensional heat flow.

2. The numerical calculated and experimental temperature values have shown excellent agreement and, consequently, a high reliability grade for the IHTC.

3. The IHTC values during the vertically upward unidirectional solidification of a eutectic Al–Si casting have varied between about 19–9.5 kW/m2 K and 6.5–5 kW/m2 K on copper and steel chills, respectively. These values have shown good agreement with those in the literature.

4. The results have shown that the receding of the casting from both the copper and steel chill surfaces does not occur during the solidification.

5. The IHTC could be affected mainly by the contact position and area between the casting and chill surfaces roughness. Future investigation should, therefore, take these effects into consideration.

Determination of unidirectional heat transfer coefficient duringunsteady-state solidification at metal casting–chill interface

Turkey

Received 9 October 2004; accepted 30 March 2005

Available online 11 May 2005

Abstract

In this study, the interfacial heat transfer coefficient (IHTC) for vertically upward unidirectional solidification of a eutectic Al–Si casting on water cooled copper and steel chills was measured during solidification.

A finite difference method (FDM) was used for solution of the inverse heat conduction problem (IHCP). Six computer guided thermocouples were connected with the chill and casting, and the time–temperature data were recorded automatically. The thermocouples were placed, located symmetrically  , at 5 mm, 37.5 mm and 75 mm from the interface. As the lateral surfaces are very well heat isolated, the unidirectional solidification process starts vertically upward at the interface surface. The measured time–temperature data files were used by a FDM using an explicit technique. A heat flow computer program has been written to estimate the transient metal–chill IHTC in the IHCP. The experimental and calculated temperatures have shown excellent agreement. The IHTC during vertically upward unidirectional solidification of an Al–Si casting on copper and steel chills have varied between about 19–9.5 kW/m2 K and 6.5–5 kW/m2 K, respectively.

Energy Conversion and Management 47 (2006) 19–34

1. Introduction

The subject of metal–chill interfacial heat transfer, because of its important influence on the solidification rate of metal castings, has been investigated by several previous studies. Some researchers have studied the heat transfer mechanism of castings to find the influencing factors on the IHTC as well as the macro heat transfer values. In these previous works, the IHTC has been dependent on many factors including the presence and thickness of surface coatings, casting surface orientation and casting size, chill or mold material, applied pressure, alloy type and composition ,liquid alloy surface tension, mold and chill preheat, alloy superheat and chill surface roughness [1–11]. The effects of the direction of gravity in relation to the interface have been examined by investigation with the chill placed on the bottom, top or side of the mold [1].

An exact estimation of the heat transfer during the liquid alloy solidification in a casting mold depends on determination of the boundary conditions during the solidification, properties of them old , properties of the casting alloy temperature distribution in the casting. During the solidification ,these parameters are changing as a function of temperature and time. For the purpose of accurate modeling of solidification processes, it is required that correct boundary conditions should be set up [12–14].

Estimation of the heat transfer coefficient in a metal casting–chill interface is usually calculated from time–temperature data measured during the solidification of a unidirectional chilled experimental casting. The casting alloy and chill material used for experimental casting are, generally ,made of some materials and alloys on which accurate knowledge of their thermophysical behavior is known, such as aluminum, copper, iron and steal [15,16]. Heat transfer coefficients differ depending on the different experimental conditions and casting alloys used [4].

Reviewing the literature, it has been found that there are basically two methods to measure the IHTC [17,18]. One is to measure the size of the gap formed between the metal casting and the chill and correlate this gap size with the heat transfer coefficient [19–21]. The other method is to conduct temperature measurements in the casting and in the chill at several designated locations and use an inverse method to derive the IHTC [1,5,14].

Some researchers have studied the problem of measuring the transient metal–chill IHTC during unidirectional solidification. These studies show that the heat transfer coefficient becomes a high value in the initial stage of solidification and then declines to a low steady value because the casting contracts from the chill surface, creating an interfacial gap [1,12,17,22,23]. It has been found that the heat transfer coefficients have higher values when solidification is vertically upward than when solidification is either vertically downward or horizontal [1].

The loss of heat when a metal first comes into contact with the mold is regulated not only by the heat storage capacity of the mold material but also by the heat transfer conditions within the metal itself and particularly at the metal–chill interface. Santos determined that the solid bodies are only in contact at isolated points, and the actual area of contact is only a small fraction of the nominal area [12].

Various processing parameters and their effect on the IHTC have been examined by several researchers. In the literature, several researchers have studied the problem of determining the IHTC at the metal–chill interface for solidifying aluminum alloys in copper, steel or cast iron molds and have provided some widely divergent values. These values have been reported from as high as 20 kW/m2 K to less than 1 kW/m2 K [1,10,24–35].

The objective of our work is to determine the metal–chill IHTC during the unidirectional solidification vertically upward of a cylindrical Al–Si alloy casting on the water cooled surface of copper and steel chills and to compare the IHTC of the copper and steel chills. In the course of the work, a heat flow computer program has been written to estimate the transient metal–chill IHTC in the IHCP.

2. Experimental procedure

The schematic representation of the experimental setup connected to the data logger and analysis system, the casting arrangement and the position of the thermocouples used in the unidirectional solidification experiments is shown in Fig. 1. Two groups of experiments for evaluation of the IHTC are conducted for a liquid alloy (Al–Si) on water cooled steel and copper chills at the Faculty of Technology in Gazi University, Ankara, Turkey. Liquid metal is cast in a ceramic mold made of an alumina-silicate refractory tube of length 290 mm, internal diameter 28 mm and wall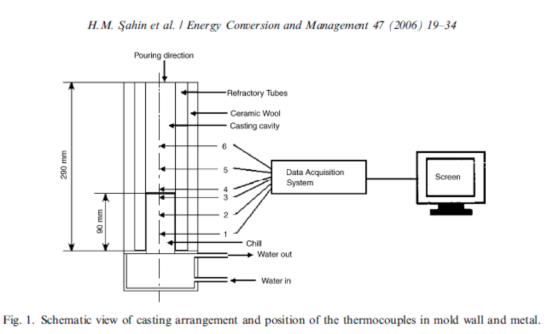 

thickness 10 mm. The refractory tube is imbedded in ceramic wool of 20 mm thickness for improved lateral heat isolation. The cylindrical chill (copper or steel) of length 90 mm is inserted into a cylindrical mold as shown in Fig. 1. Six chromel-alumel thermocouples were centered at the common cylindrical axes of the chill and casting in the radial direction (see Fig. 1). They are placed symmetrically and located at 5 mm, 37.5 mm and 75 mm from the casting–chill interface. All thermocouples were connected by cables to a data logger interfaced with a computer.

The thermophysical properties of the casting and chill materials selected for our experiments are summarized in Table 1 [36,37]. The experiments are performed with an Al–Si alloy, a eutectic composition, having a very narrow freezing range. For benchmarking purposes, copper and low carbon steel metals are used for the chill body material because of their very well known thermophysical behavior.

The vertical solidification apparatus is designed to permit heat extraction only through the water cooled bottom. The lateral surfaces are very well heat isolated, so that the unidirectional solidification process starts vertically upward at the interface surface.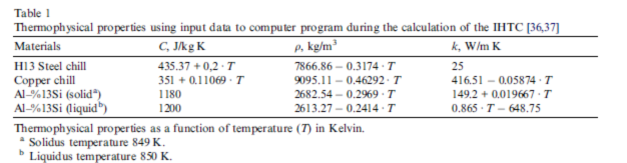

The alloy was melted in an electric resistance oven until the molten metal alloy reached a predetermined temperature (980 K), above their melting temperature of 849 K, and then cooled to room temperature in the mold. Calibrated thermocouples were used.

Six computer guided thermocouples were connected with the chill and casting, and the time–temperature data were recorded automatically. The data from the thermocouples, read in the chill and casting are used to plot the time-dependent experimental temperature profiles. The measured time–temperature data files were used to find the correct boundary conditions as well as to correlate the temperatures derived from the FDM using an explicit technique, which was incorporated in the heat flow computer program written to estimate the transient metal–chill IHTC, as explained in Chapter 3. The flow chart shown in Fig. 2 gives an overview of the solution procedure.

3. Determination of heat transfer coefficient

In our study, the IHTC during the solidification process is calculated by solving the IHCP using a FDM. Experiments are conducted to determine the unknown temperatures and the heat flux at the interface between the casting and chill. The time–temperature data are reproduced to be used to evaluate the boundary conditions.

The heat flux across the metal–chill interface can be described by a macroscopic average metal–chill IHTC (h). One can write

where _q is the average heat flux across the metal–chill interface in W/m2 and TC and TM are the calculated interface temperatures of the casting metal surface and the chill surface, respectively.

The heat flux for both the casting and chill interfaces were calculated from the temperature gradient at the surface and sub-surface nodes as follows:

where k is the thermal conductivity of the casting or chill materials, W/m K. Then, the macroscopic average IHTC (h) was calculated from Eq. (1).

3.1. Mathematical formulation of heat transfer coefficient

3.1.1. Heat flowin the chill

With adequate insulation of the chill and casting chamber, the heat flow through the casting

can be reasonably approximated as a one dimensional heat transfer problem. Unsteady state (transient) conduction heat transfer in a one dimensional body can be described by  

where T is the temperature, t is the time and x is the Cartesian coordinate. The term a is the thermal diffusivity of the conducting material,

where k is the thermal conductivity, q is the density and c is the specific heat capacity.

3.1.2. Heat flow in the casting

When treating the casting heat flow, the governing equation is similar to Eq. (3), but the term q is included on the left hand side of Eq. (3). We can write the heat transfer equation for solidifying metals as below.

The term q on the left hand side of Eq. (5) is a heat source term, which is incorporated to account for the latent heat of solidification, given by

where l is the latent heat of fusion and fs is the solid fraction in the casting. The fs term is determined

as below, Eq. (7).

The term  in Eq. (6) can be related to temperature as follows

Substitution of Eq. (8) into Eq. (6) gives

Substitution of Eq. (9) into Eq. (5) gives

This equation can be rearranged as

One can define c0 as an apparent specific heat during the solidification. Then, Eq. (11) can be written as

3.1.3. Finite difference formulation

Analytical methods may be used, in certain cases, to evaluate exact mathematical solutions to steady, one or two dimensional conduction problems. However, these solutions can be generated for an assortment of simple geometries and boundary conditions, and they are well documented in the literature. On the other hand, analytical solutions to transient problems are restricted to simple geometries and boundary conditions. In this respect, in many cases, the geometry and boundary conditions preclude the use of analytical techniques and recourse must be made to FDM. Some researchers developed a numerical model based on a FDM for simulating solidification behavior [38–40].

In the present work, this problem has been approached in one dimensional geometry for a region with a finite dimension L shown in Fig. 3 as follows:

The region (0 6 x 6 L) is divided into M equal size meshes.

m subscripts are used to designate the x location of the discrete nodal points in Fig. 3. Besides being discretized in space, the problem must also be discretized in time. The integer p is introduced for this purpose:

The finite differenc   全套毕业设计论文现成成品资料请咨询微信号：biyezuopin QQ：2922748026     返回首页 如转载请注明来源于www.biyezuopin.vip