|
nt-size: 12pt;'>样本熵测量生理信号的规律性,与模式长度无关。如果一个数据集的SampEn值高于其他给定的模式长度(m)和相似准则(r),则它仍然高于所有不同的m和r值。因此,SampEn是比较一致的,减少了近似熵[ 80 ]的偏差。高SampEn值表示信息高度不可测,低SampEn值意味着信号是可预测的。SampEn值可由下式得到:

其中,A包含了长度为m+1的向量对的总数,B包含了长度为m的向量对的总数。在本研究中,m的值取为2 [ 89 ]。该熵的优点是:(i)可用于短序列的噪声数据,(ii)能够区分各种系统,(iii)与随机数理论相比,它比近似熵性能好得多[ 80 ],(iv)保持相对的一致性[ 80 ],(v)不需要计算自身匹配,从而降低了偏差,以及(vi)熵值在不同的模式长度上更一致。然而,这种熵的主要缺点是对于稀疏数据的不一致性[ 80 ]。
2.2.4 谱熵(SEN)
谱熵是归一化的Shannon熵,采用时间序列的功率谱幅值分量进行熵评价[ 86,34 ]。它量化了脑电信号的频谱复杂度。SEN通过每个频率的功率 pf与pf的对数相乘,再将结果乘以-1获得。SEN由下式得到:

香农熵(ShEn)是一组关系参数的量度,与可能性的对数成线性变化关系[ 54 ]。它也是一种度量数据扩散的方法,最常用于评估系统的动态顺序[ 86 ]。
ShEn的主要优点是,它更好地适应正态分布[ 94 ]。然而,这种熵的缺点是:(i)由于聚集会丢失更多信息的可能性;(ii)如果使用过多区域,此熵值可能会过高[41];(iii)此方法不能解释从时间序列信号中提取不同值的时间关系[ 33 ]。
2.2.5 Renyi熵(REN)
Renyi熵是ShEn熵的一种广义形式,用于估计一个时间序列信号的谱复杂度[79]。从数学上讲,Renyi熵可以由下式得到:

其中,阶数α≠1,pi定义了总的光谱功率。REN中,α≥2 提供了平滑熵的下界,α=2类似于ShEn,将产生少量的平滑熵[ 18 ]。在本研究中,我们选择α=2。
REN的显著优点是:(i)在变量增加或减少时,该熵会随着常量的增加而变化,及(ii)对于不同的密度函数,它保持不变。换句话说,它不随使用的密度函数而变化 [91]。主要缺点是它不是一个递归的子加法,也不具有分支性和和属性[ 8 ]。
2.2.6 排列熵(PE)
排列熵是通过识别时间序列信号之间的耦合来估计时间序列的复杂度 [13,19,101]。通过评估给定时间序列信号中不同元素的排列模式存在与否,可以得出与脑电信号相关的动力学参数。在高频率下,排列熵随时间序列的不对称性而升高,而在低频时,对应于波峰和波谷的排列很少。PE由下式得到:

其中,pj代表可能的序列模式的相对频率,n表示n≥2的排列顺序。在这项研究中,我们选择嵌入维数为3,延迟为1 [ 68,13,81 ]。
排列熵是动态噪声下混沌和非平稳时间序列信号的一种度量方法。该方法鲁棒性强,效率高,不产生噪声数据,具有快速的响应。因此,它可以用来处理庞大的数据集,而不需要对数据进行预处理和对复杂参数进行微调[13]。
该熵的优点是:(i)简单、鲁棒性好,不易计算复杂度[ 55 ],(ii)适用于真实的噪声数据,(iii)不需要任何模型假设,适用于非线性分析过程[ 108 ],和(iv)适用于分析庞大的数据集,需要较少的预处理时间和参数微调[ 108 ]。主要的局限性是它无法区分特定设计的良好定义模式[ 30 ]。
2.2.7 Tsalli熵(TE)
它有助于描述系统的物理行为。它描述了具有长期记忆效应、长程相互作用和多重分形空间——时间约束的系统[ 15 ]。Tsalli系数有助于区分脑电棘波、脉冲和连续节奏。数学上,TE被定义为:

其中,q用来衡量非一致性,pi描述了具有W微观结构的离散概率集 [96]。在本研究中,我们取q=2。TE可以用来测量与ShEn不同的时间序列信号中的突变和长期记忆效应。它是表征分形随机过程的一个建设性的工具。
这个熵的优点是:(i)这种方法有助于在测量广义系统的不确定性,(ii)它更适合于处理非高斯问题[ 94 ],及(iii)它可以提供比传统的香农熵更详细的信息,特别是用于评估不同节奏和突发脑电图分析[ 20 ]。
其主要缺点是指数的选择,在进行计算时是随机的,不具有任何自动化的方法或理论[ 82 ]。
2.2.8 模糊熵(FE)
它代表了随机性信息,被定义为元素具有不同程度隶属熵的模糊集合。隶属函数在单位间隔0和1时有所不同。模糊熵定义如下:

其中A是模糊变量,Cr是可信度度量[ 50 ]。模糊熵主要测量高度不规则信号中的模糊不确定性,而ShEn熵主要处理概率不确定性问题。这种熵的优点是,它对噪声不敏感,而对信息内容的变化非常敏感[ 74 ]。
2.2.9 小波熵(WE)
正交离散小波变换(ODWT)是动态脑信号研究中的一种定量方法。ODWT定义相对小波熵,以进行脑电信号中不同频带的相对能量的测量。它计算信号不同部分之间的相似程度,而WE是一种与多频率信号响应相关的无序度的量度[ 83 ]。小波熵由下式得到:

其中,pi定义了时间序列信号的概率分布,i 定义了定义不同的分辨率水平。小波熵可以用来识别信号的基本情节行为,它可以为周期性单频信号提供有效的结果。
这种熵的优点是可以检测非平稳信号中的细微变化(83),需要较少的计算时间,能够容易地消除噪声干扰,性能不依赖于任何参数。
2.2.10 归一化双谱熵(S1,S2)和相熵(PhEn)
二阶测度,如自相关函数或功率谱,提供了随机过程的部分解释。将功率谱的原理推广到高阶被称为HOS,可以确定波形的细微变化和形状。HOS不包含高斯过程的附加信息,因为它是由二阶统计量完全定义的。因此,何一个高斯过程的HOS都为零[ 71,70 ]。
HOS是不规则信号的高阶矩的谱表示。它能够检测非线性和偏离高斯的程度,并能保持信号的相位特性 [71,72 ]。两种方法可用来估算HOS。分别是:(a)间接法:先估计累积函数,然后求傅立叶变换,(b)直接法:分段平均处理。
在直接法中,数据被划分为具有相同数量的重叠块的段。利用快速傅立叶变换(FFT)计算每个重叠块和“原始”HOS的谱系数结果。原始HOS的加权平均产生第三阶矩,被称为双谱。它包含两个频率(f1和f2),由下式得到:
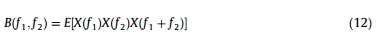
其中,X(f)是信号X(nT)的傅立叶变换。这是一个复杂的数,可分析三个频率分量之间的相互作用(f1,f2,f1+f2)。频率f可以0和1之间的奈奎斯特频率之间归一化。
双谱熵提出[ 23 ]了归一化双谱熵,类似于谱熵[ 43 ],

其中,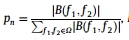 ,N是整数。 ,N是整数。
双谱平方熵,
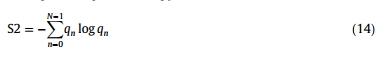
其中,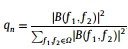 ,N是整数。 ,N是整数。
相熵(PhEn),
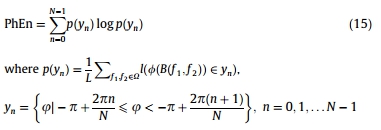
其中,N是整数,L是Ω内的点数,φ是双谱相角,l是指标函数(当相角在yn范围内,l=1)。
HOS熵的一些优点是:(i)这是一种第三阶统计分析以及一种高信噪比(SNR)的非线性方法[ 71,72,70 ],(ii)它可以捕捉其频率分量和相位耦合之间的相互作用[ 72 ],及(iii)它能准确捕捉生物信号的微妙变化[ 24,25 ]。
2.2.11 递归量化分析熵(RQAEn)
它是线段分布中所包含的平均信息的度量。这是一种基于状态空间轨迹的递归定量分析(RQA)方法。它有助于量化动态系统递归的次数和持续时间[109]。RQA可以测量时间序列信号的隐周期,并可根据其复杂度和非线性来表示非平稳输入信号[109]。
递归熵有助于有助于检测混沌、混沌转换、不稳定周期轨道、时滞,并从短和非平稳输入数据中提取有用信息[ 61 ]。
3. 熵特征的统计研究
本文中,所有提取的熵特征都可进行统计分析,以确定临床意义上的三种分类(正常、发作间期和发作期)。特征通过方差分析(ANOVA)统计试验进行测试[ 49 ]。试验确定了三种特征组的F值和P值(概率值)。F值和P值呈负相关。
因此,高F值特征值的P值接近于零,反之亦然。其他方法如Bhattacharyya距离[28,29],Wilcoxon符号秩检验[ 40,107 ],接受者操作特征曲线(ROC)[ 84 ]和模糊最大相关和最小冗余(MRMR)[ 12 ]也可以用来进行排序。十重交叉验证法可用于开发自动化系统。约90%的熵特征被用于训练,约10%用于测试数据集。这是帮助开发强大分类器和高效诊断系统的标准方法[ 16 ]。
总共13个熵特征,如近似熵(APEN),模糊熵(FE)、样本熵(SampEn),Renyi熵(REN),谱熵(SEN),排列熵(PE),小波熵(WE),Tsallis熵(TE),相熵(PhEn),双谱熵(S1)、双谱平方熵(S2)、Kolmogorov–Sinai熵(KSE)和递归定量分析熵(RQA En)从300个脑电图中提取出来(O、F和S集合均100个)。表1给出了三种不同分类——正常、发作间期和发作期的平均值和标准差(SD)熵值。
从正常,发作间期和发作期脑电图信号中提取出来的各种特征为三种分类提供了有效的区分(P<0.0001)。
这些特征可以通过P值进行评估,具备良好的区分能力。可以使用ANOVA F值来排列所有熵特征。据悉,癫痫发作时大脑活动的可预测性比非发作期要高,可通过熵值的突然下降反映出来[ 37,1,48,42 ]。 从表1列出的结果可以看出,大部分的熵特征最适合于癫痫脑电信号的分类。在这些熵中,Renyi熵、香农熵、SEN和PE占据最高地位,具有更高区分性的F值。
F值有助于表征熵的性能,具备最高F值的特征区分效果最好,可以有效区分正常、发作间期和发作期。因此,可以推测,各种熵的汇总有助于提高分类率。
4. 有关工作的讨论
各种研究报告都可将EEG信号自动分成两类,三类和五类癫痫类。下面简要描述它们。
4.1 两类:正常和癫痫发作信号
Kannathal等人[45,46]使用了多种熵特征,即Kolmogorov–Sinai熵、近似熵、Renyi熵和Shannon熵来区分癫痫和正常脑电信号。在提取的四个熵特征中,在正常脑电图与癫痫脑电信号的鉴别中,Kolmogorov–Sinai熵优于其他熵(P值<0.05)。研究报告使用自适应神经模糊推理系统(ANFIS)分类器,分类准确率在90%左右。Polat等人[ 77 ]结合快速傅立叶变换(FFT)特征提取技术和决策树(DT)分类器,开发了癫痫检测算法。该算法使用基于Welch的FFT法从EEG记录中提取出功率谱密度特征。使用DT分类器的分类精度达98.72%。
Srinivasan等人[ 92 ]应用近似熵建立基于神经网络的癫痫自动检测分类工具。该算法从EEG信号中提取ApEn,作为概率神经网络(PNN)分类器的输入信号。实验结果表明,从癫痫EEG信号中区分正常状态的准确率为100%。
Ocak [ 73 ]使用离散小波变换(DWT)分离了正常和癫痫脑电信号。将近似熵应用于离散小波变换系数,得到了96%的分类精度。Kumar等人[ 51 ]将DWT用于正常和癫痫脑电信号,并使用ApEn算法进行特征提取。他们使用前馈反向传播神经网络分类器获得了100%的分类精度。在Kumar[ 52 ]等人进行的另一项姐妹研究中,通过时会用DWT、ApEn以及支持向量机(SVM)分类器也获得了100%的分类精度。 Liang 等人[ 57 ]计算出了从正常和癫痫脑电信号中提取的谱系数的近似熵。具有径向基核函数(RBF)的支持向量机通过21个特征获得了98.3%的准确率。Shen等人[ 88 ]用样本熵与SVM分类器对正常和癫痫脑电信号进行分类,准确率达99.2%。
有几项研究探讨了排列熵特征[ 68 ],小波熵特征[ 53102 ]和多离散小波变换形式[ 10 ],实际分类精度超92%。Liang等人[ 57 ]从正常和癫痫脑电信号中提取的谱系数计算出了近似熵。使用了SVM和RBF,对21个特征进行提取,获得了98.3%的分类精度。Shen等人[ 88 ]利用样本熵和支持向量机分类器对正常和癫痫脑电信号进行分类,准确率为99.2%。Ahammad等人[ 9 ]应用能量谱熵、标准差、最大值、最小值和平均DWT线性分类器对CHB-MIT数据库的数据分析,实现98.5%准确性。Gandhi等人[ 36 ]使用离散小波变换、谱熵和能量特征,结合PNN分类器对两类(正常和癫痫)问题进行分类,准确率达100%。
表1使用各种熵分类正常,发作间期和发作期的结果(平均值和标准差),P<0.0001
|
特征
|
正常
|
|
|
发作间期
|
|
|
发作期
|
|
F-值
|
|
|
平均值
|
标准差
|
|
平均值
|
标准差
|
|
平均值
|
标准差
|
|
|
REN
|
—1.90E+01
|
5.23E—01
|
|
—1.89E+01
|
1.12E+00
|
|
—2.18E+01
|
1.12E+00
|
290.8153
|
|
SampEn
|
1.45E+00
|
9.71E, —02
|
|
1.13E+00
|
1.90E—01
|
|
1.09E+00
|
1.44E—01
|
177.2937
|
|
SEN
|
—4.74E+06
|
1.52E+06
|
|
—5.27E+06
|
4.48E+06
|
|
—2.73E+07
|
1.68E+07
|
163.5236
|
|
PE
|
1.39E+00
|
1.00E—01
|
|
1.44E+00
|
8.42E—02
|
|
1.24E+00
|
8.85E—02
|
132.8653
|
|
FE
|
2.34E+00
|
2.04E—01
|
|
1.56E+00
|
3.13E—01
|
|
1.82E+00
|
4.86E—01
|
126.7034
|
|
TE
|
—2.12E+07
|
1.18E+07
|
|
—3.36E+07
|
9.09E+07
|
|
—4.77E+08
|
4.13E+08
|
112.9842
|
|
ApEn
|
2.27E+00
|
3.32E—02
|
|
1.86E+00
|
3.31E—01
|
|
1.93E+00
|
2.15E—01
|
91.7992
|
|
WE
|
—7.03E+07
|
5.97E+07
|
|
—2.32E+08
|
9.92E+08
|
|
—2.75E+09
|
2.54E+09
|
91.3993
|
|
RQAEn
|
2.93E—02
|
5.91E—03
|
|
5.75E—02
|
4.81E—02
|
|
9.14E—02
|
3.91E—02
|
74.7212
|
|
S1
|
5.86E—01
|
7.26E—02
|
|
4.51E—01
|
9.15E—02
|
|
5.01E—01
|
9.21E—02
|
62.9000
|
|
S2
|
3.49E—01
|
1.06E—01
|
|
1.83E—01
|
9.62E—02
|
|
2.75E—01
|
1.30E—01
|
55.1414
|
|
PhEn
|
3.38E+00
|
1.14E—01
|
|
3.05E+00
|
4.58E—01
|
|
3.10E+00
|
2.32E—01
|
35.4182
|
|
KSE
|
7.05E—03
|
1.35E—02
|
|
2.45E—02
|
5.26E—02
|
|
3.36E—02
|
7.55E—02
|
6.3297
|
4.2 两类:发作间期(N或F类)和发作期(癫痫S)信号
少数的几项研究评估了描述两类(即发作间期和发作期)脑电信号中的熵特征。Yaun等人[ 106 ]提出了一种区分发作间期和发作期脑电信号的方法,他们采用非线性动力学特征,通过去趋势波动分析(DFA)、Hurst指数和ApEn来计算标度系数。使用了两个包含脑电图发作间期和发作期的数据集。研究利用极端学习机(ELM)算法训练单隐层前馈神经网络,对脑电信号特征进行了分类。他们报告的分类精度为96.5%。Song等人[ 90 ]结合ELM,采用优化的样本熵算法来区分发作间期和发作期的脑电图信号,报告的准确性为99%。最近,Zhang等人[ 110 ]使用ApEn提出了自动识别发作间期和发作期EEG信号的方法。研究收集了四位部分性癫痫发作病人的脑电(发作间期和发作期)信号记录。从四位病人信号提取的ApEn特征通过支持向量机分类器进行自动分类。研究报告的确定发作间期和发作期的精度为93.33%。Xiang等人[ 105 ]提出了一种利用模糊熵(FE)检测脑电信号中无癫痫发作和癫痫发作状态的算法。研究采用两个数据集进行两种实验分类:(i)基于N和S数据集分类发作间期和发作期(从对面大脑半球的海马体区和致发作活动区记录到的脑电信号)和(ii)基于 F数据集分类发作间期和发作期(从致痫区和发作活动区记录到的脑电信号)。该算法计算了EEG信号的不同癫痫状态,然后经下一步SVM分类器作用。他们的研究结果:分类准确度100%,灵敏度100%,且在分类发作间期和发作期脑电图信号的特异性为100%(N和S的数据集)。同时,也获得了88.5%的准确度,90.36%的灵敏度,且分类发作间期和发作期脑电图信号特异性87.63%(F和S数据集)。Bruzzo等人[ 17 ]利用排列熵(PE)从发作间期和癫痫脑电信号中提取特征。他们观察到的曲线下面积(AUC)为0.85,使用接受者操作曲线(ROC)绘图。Aarabi等人[ 1 ]对弗莱堡癫痫预测EEG数据库中采集的发作间期和癫痫数据进行了熵特征研究。通过基于频率和时间分析的模糊规则分类获得的分类准确率为98.7%。Li等人[ 56 ]用PE特征为对发作间期和癫痫数据分类,观测到熵值从无癫痫发作至发作期逐渐降低。
4.3 三类:正常、发作间期(N或F)和发作期
一些研究人员开发出了最先进的方法,将脑电信号分类为正常、发作间期和发作期,以便于更好的诊断、预测和治疗。最近,Acharya等人[ 7 ]将连续小波变换(CWT)应用到脑电信号。高阶谱(HOS)和纹理特征从CWT图中提取出来,然后被馈送到四个不同的分类器:DT、PNN、SVM和k-近邻(KNN)分类器。他们发现,支持向量机分类器与RBF相结合产生了最高的分类准确率96%,敏感性96.9%,特异性97%。他们得出结论,他们的技术可以用作一种癫痫发作的自动监控软件。Martis等人[ 60 ]探索了一种新的时频非线性方法——固有时间尺度分解法(ITD)。ITD表示法被用来确定脑电信号和显著能量的微妙变化,还可用来计算分形维数(FD)和SampEn特征。这些特征然后被馈送到DT分类器,分别获得了95.6 %、99%和99.5%的分类准确性、灵敏度和特异性。Kumar等人[ 52 ]使用模糊近似熵模糊来评价五个健康人(睁眼和闭眼)和癫痫病人的 EEG信号记录。在他们的研究中,利用小波变换将脑电信号分解成不同的频率子带信号,并计算出这些子带的模糊近似熵。研究报告中,模糊近似熵特征在两类信号(发作间期和发作期脑电图信号)和三类(正常、发作间期和发作期脑电图信号)的分类中是重要的。使用SVM分类器后,报告的正常VS发作信号准确度为100%,正常数据(睁眼)99.3%,正常(闭眼)VS发作信号99.65%。此外,在区别发作间期和发作脑电信号时,还获得了99.6%的精度(SVM-RBF)和99.85%(SVM线性)的精度。Chua等人[ 24 ]利用双谱熵和相熵,结合高斯混合模型(GMM)分类器,在区分发作间期和发作期EEG信号时获得了93%的准确度。在Chua等人[ 25 ]的另一项连续研究中,从HOS和功率谱中提取出了区分正常、发作间期和发作期EEG信号的特征。比较了使用HOS 特征和功率谱特征得到的分类精度。研究表明,结合高斯混合模型分类器,使用HOS特征产生了比谱特征较高的准确度,两者分别为93.1%和88.7%。Acharya等人[ 5 ]集合模糊分类器,利用ApEn、SampEn、相熵(S1和S2),在对正常、发作间期和发作期EEG信号区分时,获得了98.1%的准确度。在另一项同组人员的研究中,他们使用模糊分类器[6],利用熵、HOS、FD和Hurst指数特征,获得了99.7%的分类精度。Quiroga等人[ 78 ]使用Kulback–Leibler和重整化熵将正常和癫痫EEG信号分为三类。他们的结论是,Kulback–Leibler比重整化熵提供了较好的分类结果。递归图(RP)和递归定量分析(RQA)参数在分类正常、发作期和发作间期脑电图信号中也被用了进来。Acharya 等人[ 4 ]使用10种RQA特征对三种EEG数据段类型进行了分类。他们使用七种分类器,如DT、SVM、GMM、KNN、PNN、模糊Sugeno 分类器(FSC)和朴素贝叶斯分类器(NBC)来评价其性能。他们观察到,SVM分类器产生了最高的准确性95.6%,敏感性和特异性分别为98.9%和97.8% 。Song和Lio [ 89 ]结合ELM, 将SampEn应用于正常、发作间期和发作期脑电图段,实现了95.7%的准确性。Marties等人[ 59 ]利用经验模式分解(EMD)和决策树(C4.5)分类器对光谱熵特征进行了探索。利用EMD对脑电信号进行分解,得到振幅和频率调制波的固有模态函数(IMF)。从每个IMF段提取谱峰、光谱熵和能量等光谱特征。将这些特征反馈到C4.5决策树分类器,得到95.3%的准确率。
表2基于熵特征的癫痫自动检测研究综述

作者 方法 准确度 (%) 数据库

处理两类(正常与癫痫)问题的研究
|
Kannathal等人 [46]
|
熵措施——ANFIS
|
92.2
|
波恩大学——德国
|
|
Srinivasan 等人[92]
|
ApEn-Elman网络
|
100
|
波恩大学——德国
|
|
Ocak [73]
|
离散小波变换系数和分类器+ApEn
|
96
|
波恩大学——德国
|
|
Kumar等人 [51]
|
DWT+ApEn-前馈反向传播神经网络
|
100
|
波恩大学——德国
|
|
|
|
|
|
|
Kumar 等人 [52]
|
DWT+ApEn-SVM
|
100
|
波恩大学——德国
|
|
Nicolaou和
|
PE-SVM
|
93.5
|
波恩大学——德国
|
|
Georgiou [68]
|
|
|
|
|
Wang 等人[102]
|
小波包熵分层
|
99.4
|
波恩大学——德国
|
|
Akareddy 和
|
Multi-DWT+改进的ApEn-ANN
|
90
|
CHB–MIT [22]
|
|
Kulkarni [10]
|
|
|
|
|
Liang等人[57]
|
AR模型和ApEn(共21个功能)-SVM(RBF)权重
|
98.3
|
波恩大学——德国
|
|
|
|
|
|
|
Shen等人[88]
|
SampEn-SVM-GA
|
99.2
|
私人数据库
|
|
Kumar等人[53]
|
小波熵-Elman网络
|
99.2
|
波恩大学——德国
|
|
Ahammad等人[9]
|
能量,谱熵,标准差,最大值,最小值和平均DWT分类器
|
98.5
|
CHB–MIT/波恩大学——德国
|
|
|
|
|
|
|
|
|
|
|
|
Gandhi等人[36]
|
离散小波变换-谱熵+能-PNN
|
100
|
私人数据库/波恩大学——德国
|
处理两类问题(发作和癫痫)的研究
Song等人[90] 优化的-SampEn-ELM 99 波恩大学——德国
Yuan等人 [106] ApEn/Hurst 指数/DFA-SVM/ANN 96.5 波恩大学——德国
Aarabi等人[1] 熵频率和时间分析模糊规则98.7 弗莱堡癫痫预测EEG(FSPEEG)数据库[58]
Zhang等人[110] ApEn-SVM 93.3 私人数据库
Bruzzo等人 [17] PE-ROC AUC = 0.85 私人数据库
Li 等人 [56] PE PE从无发作期到发作期逐渐降低
私人数据库
Xiang等人[105] FE-SVM 98.3-CHB–MIT 100–Bonn CHB–MIT/波恩大学
处理三类问题的研究(正常、发作间期和发作期)
Chua等人 [24] S1,S2和双谱幅值-高斯混合模型
93.1 波恩大学——德国
Chua等人[25] 幅值+PhEn, S1和 S2-GMM 93.1 波恩大学——德国
功率谱+GMM 88.7
Acharya等人 [3] 非线性参数 – ApEn,高斯混合模型
95 波恩大学——德国
Acharya 等人[5] ApEn, SampEn, PhEn, S1和S2 – 模糊 98.1 波恩大学——德国
Acharya等人 [6] 熵+HOS+Higuchi FD+Hurst-Fuzzy 99.7 波恩大学——德国
Acharya 等人 [7] CWT+S1+S2+PhEn+纹理-SVM 96 波恩大学——德国
Martis 等人[59] SEN-EMD-C4.5 95.3 波恩大学——德国
Martis 等人[60] SampEn-DT 95.7 波恩大学——德国
Song 和 Lio [89] SampEn-ELM 95.7 波恩大学——德国
Acharya 等人[4] RE+RQA-SVM 95.6 波恩大学——德国
Quiroga等人 [78] Kulback-Leibler和重整化熵 KL熵比重整化熵更好地区分发作和背景脑电图 波恩大学——德国
处理五类问题的研究(正常——两类VS发作间期——两类VS发作期)
Guo等人[39] 多小波变换+熵MLPNN 98.2 波恩大学——德国

4.4 五类:正常(两类),发作间期(两类)和发作期信号
研究人员已经研究了五组基于小波技术的EEG信号:正常(两类信号,睁眼和闭眼或数据集Z和O信号)、发作间期(两类–数据集N和F信号)和发作期段[ 38 ]。
Guo等人[ 39 ]将多小波变换与ApEn应用到正常和癫痫脑电信号中,并结合了多级概率神经网络(MLPNN)分类器。在他们的报告中,分类正常(两组数据集信号)、发作间期(两类)和发作期的精度为98.2%。表2表明,不同的研究人员尝试了不同的熵进行脑电信号分析和分类。许多研究者[ 106,90110105 ]使用一种熵特征进行脑电信号分析,分类正常、发作间期和发作期的精度为92%。其他一些研究人员[45,46,5–7,24,25]使用了多种熵的组合来检测正常、发作间期和发作期EEG信号。不同熵的组合在脑电信号分类准确率超过92%。因此,不同熵组合可以提高分类效率。换句话说,不同熵组合应该是这样的(不同熵组合的主要优势),可以通过增加多种熵来克服一种熵的缺陷问题。
本文中,使用了不同的熵来分类正常、发作间期和发作期的脑电图信号。结果表明,熵可以作为一个国家的最先进的方法将脑电信号分类成不同的癫痫状态。
从EEG信号中提取熵特征具有以下优点:
(i)它可用于信号处理中,以分离有用信号和冗余信息。
(ii)通常,高不规则性或不可预知性信号具有高值,高规则性信号具有低值。因此,更容易识别信号中的异常活动。
(iii)可自动识别视觉难以定位的发作段。此外,它可以用于区分病灶和非病灶脑电信号。
(iv)表1中显示的结果表明了各种熵独特的范围和其排名(使用了F值)。
(v)这些熵特征可用于其他生物医学应用,如心脏异常、眼病、糖尿病早期、老年痴呆症、自闭症、脂肪肝疾病和中风检测和治疗。
5. 结论
癫痫是一种由反复发作引起的神经系统疾病,可以用脑电图信号来评估。脑电信号呈非线性的性质,不同观察者具有不同的而变化。因此,癫痫患者脑电信号的自动检测可以在癫痫患者的监测和治疗中起到一定的作用。利用熵特征可以有效地评价脑电信号的非线性和混沌性质。它表现出EEG信号中存在的可变性和复杂性。这一全面的综述提供了各种熵区分正常、发作间期和发作期EEG信号的应用方法。表1总结了所有的熵的性能,可以得出的结论是,RE、SampEn、SEN和PE熵具有高度的区分性特征,能够很好地分类正常、发作间期和发作期EEG信号。
参考文献
[1] A. Aarabi, R. Fazel-Rezai, Y. Aghakhani, 基于模糊规则的颅内脑电信号癫痫发作检测系统, Clin. Neurophysiol. 120 (2009) 1648– 1657.
[2] B. Abibullaev, H.D. Seo, M.S. Kim, 基于连续小波变换和人工神经网络的癫痫尖峰检测, Int. J. 小波多分辨率信息处理. 8 (1) (2010) 33.
[3] U.R. Acharya, K.C. Chua, T.C. Lim, Dorithy, J.S. Suri, 基于非线性参数的癫痫脑电信号自动识别, J. Mech. Med. Biol. 9 (4) (2009) 539–553.
[4] U.R. Acharya, S. VinithaSree, S. Chattopadhyay, W. Yu, A.P.C. Alvin, 递归量化分析在癫痫脑电信号自动识别中的应用, Int. J. Neural Syst. 21 (3) (2011) 199–211.
[5] U.R. Acharya, F. Molinari, S. VinithaSree, S. Chattopadhyay, N.G. Kwan-Hoong,
J.S. Suri, 基于熵的癫痫脑电信号自动诊断, Biomed. 信号处理. 控制7 (4) (2012) 401–408.
[6] U.R. Acharya, S. VinithaSree, A.P.C. Alvin, J.S. Suri, 非线性和小波特征在癫痫脑电信号自动识别中的应用, Int. J. Neural Syst. 22 (2) (2012) 1250002-1–1250002-14.
[7] U.R. Acharya, R. Yanti, J.W. Zheng, M.M. Krishnan, J.H. Tan, R.J. Martis, C.M. Lim, 基于CWT、HOS和纹理参数实现癫痫自动诊断, Int. J. Neural Syst. 23 (2013) 1350009.
[8] J. Aczel, Z. Daroczy, 论信息测度及其表征, 学术出版社,纽约,1975.
[9] N. Ahammad, T. Fathima, P. Jospeh, 癫痫发作活动和使用EEG检测发作, BioMed Res. Int. (2014) 7 450573.
[10] S. Akareddy, P.K. Kulkarni, EEG signal classification for epilepsy seizure detection using improved approximate entropy采用改进的近似熵对脑电信号进行癫痫发作分类检测, Int. J. Pub. Health Sci. (IJPHS) 2 (1) (2013) 23–32.
[11] R.G. Andrzejak, K. Lehnertz, C. Rieke, F. Mormann, P. David, C.E. Elger,脑电活动时间序列中非线性确定性和有限维结构的表征:依赖于记录区域和脑状态, Phys. Rev. E 64 (2001) 061907.
[12] S. Ann, Q. Hu, D. Yu, 基于模糊熵的最大关联度和最小冗余特征选择,IEEE粒度计算会议,杭州,2008年8月 26–28, IEEE, 中国, pp. 101–106.
[13] C. Bandt, B. Pompe, Permutation entropy:时间序列的自然复杂性测度, Rev. Lett. 88 (2002) 174102.
[14] P.N. Banerjee, D. Filippi, H.W. Allen, 癫痫的描述性流行病学——综述, Epilepsy Res. 85 (1) (2009) 31–45.
[15] A. Bezerianos, S. Tong, N. Thakor, 脑缺血后脑电节奏变化的时间依赖性熵估, Ann. Biomed. Eng. 31 (2) (2003) 221–232.
[16] C.M. Bishop, 模式识别与机器学习(信息科学与统计学), 施普林格出版社,纽约公司,Secaucus,新泽西州,美国,2006.
[17] A.A. Bruzzo, B. Gesierich, M. Santi, C.A. Tassinari, N. Birbaumer, G. Rubboli, 基于排列熵从癫痫患者头皮脑电图检测警惕变化和发作状态 . 初步研究, Neurol. Sci. 29 (1) (2008) 3–9.
[18] C. Cachin, 平滑熵和Renyi熵,密码术进展——欧洲 ‘97, 卷1233, 施普林格,柏林海德堡, 2001, pp. 193–208.
[19] Y. Cao, W. Tung, J.B. Gao, V.A. Protopopescu, L.M. Hively, 利用排列熵检测时间序列中的动态变化, Phys. Rev. E 70 (2004) 046217.
[20] A. Capurro, L. Diambra, D. Lorenzo, O. Macadar, M. Martin, C. Mostaccio, A. Plastino, J. Perez, E. Rofman, M. Torres, J. Velluti, 人类大脑的动态变化:基于Tsallis信息测度进行脑电信号的分析, Physica A 265 (1999) 235–254.
[21] A.M. Chan, F.T. Sun, E.H. Boto, B.M. Wingeier,癫痫病发作自动检测在颅内脑电图准确起效时间测定中的应用, Clin. Neurophysiol. 119 (2008) 2687–2696.
[22] CHB-麻省理工学院数据库。<http://physionet.org/cgi-bin/atm/ATM>.
[23] K.C. Chua, V. Chandran, U.R. Acharya, C.M. Lim, 利用心率变异性高阶谱诊断心脏状态, J. Med. Eng. Technol. 3232 (2) (2008) 145–155.
[24] K.C. Chua, V. Chandran, U.R. Acharya, C.M. Lim, 癫痫病脑电信号的高阶谱自动识别,J. Eng. Med. 223 (4) (2009) 485–495.
[25] K.C. Chua, V. Chandran, U.R. Acharya, C.M. Lim, 高阶谱在癫痫病脑电图识别中的应用, J.Med. Syst. 35 (6) (2011) 1563–1571.
[26] A.G. Correa, E. Laciar, H.D. Patino, M.E. Valentinuzzi, 基于自适应滤波器的脑电信号在梯级伪影去除中的应用, J. Phys: Conf. Ser. 90 (2007) 012081.
[27] T.M. Cover, J.A. Thomas, 信息论要素, Wiley, 1991.
[28] K.G. Derpanis, 巴特查里亚度量。<http://www.cse.yorku.ca/~kosta/CompVis_Notes/bhattacharyya.pdf>, 2008 (date accessed 04.27.15).
[29] EoM- 数学百科全书,巴特查里亚距离。<http://www.encyclopediaofmath.org/index.php/Bhattacharyya_distance> (date accessed 04.27.15).
[30] B. Fadlallah, B. Chen, A. Keil, J. Principe, 加权置换熵:包含振幅信息的时间序列复杂性测度, Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 87 (2) (2013) 022911.
[31] F. Falniowski, On the connections of generalized entropies with Shannon and Kolmogorov–Sinai entropies, 在广义熵与Shannon和Kolmogorov–Sinai熵之间的连接关系, Entropy 16 (2014) 3732–3753.
[32] J.D. Farmer, 信息维数与混沌的概率结构,Z. Naturforsch 37A (1982) 1304–1325.
[33] D.P. Feldman, J.P. Crutchfield, 统计复杂性的度量:为什么? Phys Lett. A 238 (1998) 244–252.
[34] J. Fell, J. Roschke, K. Mann, C. Schaffner, ,睡眠阶段的歧视:光谱和非线性脑电图措施比较, Electroencephalogr. Clin. Neurophysiol. 98 (5) (1996) 401–410.
[35] A.J. Gabor, 采用自组织神经网络的癫痫病检测:与其他检测方法比较和相互验证, Electroencephalogr. Clin. Neurophysiol. 107 (1) (1998) 27–32.
[36] T. Gandhi, B.K. Panigrahi, M. Bhatia, S. Anand, 基于离散和声搜索的癫痫发作检测专家模型, Expert Syst. Appl. 39 (4) (2012) 4055–4062.
[37] B.R. Greene, S. Faul, W.P. Marnane, G. Lightbody, I. Korotchikova, G.B. Boylan, 新生儿惊厥检测脑电图定量特征的比较,Clin. Neurophysiol. 19 (6) (2008) 1248–1261.
[38] I. Guler, E.D. Ulbeyi, 基于小波系数的脑电信号分类自适应神经模糊推理系统,J. Neurosci. Methods 148 (2005) 113–121.
[39] L. Guo, D. Rivero, A. Pazos, 基于多小波变换近似熵和人工神经网络的癫痫检测,J. Neurosci. Methods 193 (1) (2010) 156–163.
[40] T. Hwang, C.H. Sun, T. Yun, G.S. Yi, FiGS:基于滤波器的微阵列数据基因选择工作平台, BMC Bioinform. 11 (2010). <http://www. biomedcentral.com/1471-2105/11/50>, (访问日期 04.10.15).
[41] E.J. Hekkila, L. Hu, 尺度效应和分辨率效应的空间熵测度调整, Environ. Plann. B: Plann. Des. 33 (2006) 845–861.
[42] L.D. Iasemidis, D.S. Shiau, W. Chaovalitwongse, J.C. Sackellares, P.M. Pardalos, J.C. Principe, P.R. Carney, A. Prasad, B. Veeramani, K. Tsakalis, 自适应癫痫发作预测系统,IEEE Trans. Biomed. Eng. 50 (5) (2003) 616027.
[43] T. Inouye, K. Shinosaki, H. Sakamoto, S. Toi, S. Ukai, A. Iyama, Y. Katsuda, M. Hirano, 利用功率谱熵来量化脑电不规则性, Electroencephalogr. Clin. Neurophysiol. 79 (1991) 204–210.
[44] C.J. James, 使用脑电图和人工神经网络检测脑电图中癫痫样活动,坎特伯雷大学, Christchurch, New Zealand, 1997.
[45] N. Kannathal, U.R. Acharya, C.M. Lim, P.K. Sadasivan, 脑电图特征的比较研究, Comput. Methods Programs Biomed. 80 (1) (2005) 17–23.
[46] N. Kannathal, C.M. Lim, U.R. Acharya, P.K. Sadasivan, 在脑电图中检测癫痫的熵, Comput. Methods Programs Biomed. 80 (3) (2005) 187–194.
[47] H. Kantz, T. Schreiber, 非线性时间序列分析,大学出版社,剑桥,1997.
[48] K.M. Kelly, D.S. Shiau, R.T. Kern, J.H. Chien, M.C. Yang, K.A. Yandora, J.P. Valeriano, J.J. Halford, J.C. Sackellares, 基于头皮脑电信号的自动癫痫检测系统评价, Clin. Neurophysiol. 121 (11) (2010) 1832–1843.
[49] H. Kobayashi, B.L. Mark, W. Turin, 随机过程与统计分析:在通信、信号处理、排队论和数学金融中的应用,剑桥大学出版社,2011.
[50] B. Kosko, 模糊熵与条件调节,Inf. Sci. 40 (1986) 165–174.
[51] Y. Kumar, M.L. Dewal, R.S. Anand,采用基于小波变换的近似熵和人工神经网络的脑电癫痫发作检测, SIViP 8 (7) (2012) 1323–1334.
[52] Y. Kumar, M.L. Dewal, R.S. Anand, 利用基于小波变换的模糊近似熵和支持向量机检测癫痫的发作, Neurocomputing 133 (2014) 271–279.
[53] S.P. Kumar, N. Sriraam, P.G. Benakop, B.C. Jinaga, 利用人工神经网络分类器检测癫痫发作的熵值, Expert Syst. Appl. 37 (4) (2010) 3284–3291.
[54] D.S. Lemons, 熵的学生指南,剑桥大学出版社, 2013.
[55] X. Li, G. Ouyang, D.A. Richards, 置换熵对失神发作的可预测性分析, Epilepsy Res. 77 (2007) 70.
[56] J. Li, J. Yan, X. Liu, G. Ouyang, 利用置换熵测量失神发作时脑电信号的变化, Entropy 16 (2014) 3049– 3061.
[57] S.F. Liang, H.C. Wang, W.L. Chang, 脑电复杂性与频谱分析相结合在癫痫诊断和癫痫检测中的应用, EURASIP J. Adv. Signal Process. 2010 (2010) 853434.
[58] T. Maiwald, M. Winterhalder, R. Aschenbrenner-Scheibe, H.U. Voss, A. Schulze-Bonhage, J. Timmer, 三种非线性癫痫发作预测方法的比较, Physica D 194 (2004) 357–368.
[59] R.J. Martis, U.R. Acharya, J.H. Tan, A. Petznick, R. Yanti, K.C. Chua, E.Y.K. Ng, L. Tong, 经验模态分解(EMD)在脑电信号自动检测中的应用, Int. J. Neural Syst. 22 (6) (2012) 1250027-1–1250027-16.
[60] R.J. Martis, U.R. Acharya, J.H. Tan, A. Petznick, L. Tong, C.K. Chua, E.Y. Ng, 内禀时间尺度分解(ITD)在脑电信号癫痫发作自动预测中的应用,Int. J. Neural Syst. 23 (2013) 1350023.
[61] N. Marwan, N. Wessel, U. Meyerfeldt, A. Schirdewan, J. Kurths, 基于复杂性度量的递归图及其在心率变化数据中的应用,Phys. Rev. E 66 (2) (2002) 026702.
[62] N. McGrogan, 脑电图癫痫发作的神经网络检测,牛津大学,牛津, 2001.
[63] R. Meier, H. Dittrich, A. Schulze-Bonhage, A. Aertsen,人类长期脑电图中检测癫痫发作:一种自动在线检测和分类多态性癫痫发作的新方法,J. Clin. Neurophysiol. 25 (2008) 119–131.
[64] G.R. Minasyan, J.B. Chatten, R.N. Harner, 头皮脑电图对病人早期特殊癫痫症状的检测,J. Clin. Neurophysiol. 27 (2010) 163–178
[65] M. Misiurewicz, 紧凑空间里锌作用变分原理的一个简短证明,Asterisque 40 (1976) 147–157.
[66] J. Mitra, K.R. Glover, P.Y. Ktonas, A.K. Thitai, A. Mukherjee, N.B. Karayiannis Jr., J.D. Frost, R.A. Hrachovy, E.M. Mizrahi, 自动从新生儿脑电图上检测癫痫发作的多级系统,J. Clin. Neurophysiol. 26 (4) (2009) 218–226.
[67] F. Mormann, R.G. Andrzejak, C.E. Elger, K. Lehnertz, 癫痫发作预测:漫长而曲折的道路, Brain 130 (Pt 2) (2007) 314–333.
[68] N. Nicolaou, J. Georgiou, 基于置换熵和支持向量机的癫痫脑电图检测, Expert Syst. Appl. 39 (2012) 202–209.
[69] J.J. Niederhauser, R. Esteller, J. Echauz, G. Vachtsevanos, B. Litt, 使用一个符号周期变换,从深度域脑电图检测癫痫前体, IEEE Trans. Biomed. Eng. 50 (2003) 449–458.
[70] C.L. Nikias, M.R. Raghuveer, 双频谱评价—数字信号处理框架, Proc. IEEE 75 (1987) 869–891.
[71] C.L. Nikias, J.M. Mendel, 高阶谱信号处理、IEEE信号处理。 Mag. 10 (3) (1993) 10–37.
[72] C.L. Nikias, A.P. Petropulu, 高阶谱分析:非线性信号处理框架。PTR Prentice Hall, Englewood Cliffs, NJ, 1993.
[73] H. Ocak, 基于离散小波变换和近似熵的脑电信号癫痫发作自动检测,Expert Syst. Appl. 36 (2) (2009) 2027–2036.
[74] S.K. Pal, A. Petrosino, L. Maddalena, 视频监控软计算手册,包含于:B. Chakraborty, S. Bhattacharyya, P. Dutta (Eds.), 基于视频内容模糊熵估计的无监督视频镜头边界检测技术,Chapman and Hall, 2012, p. 237 (Chapter 9).
[75] S.M. Pincus, 近似熵作为度量系统的复杂性,Proc. Natl. Acad. Sci. 88 (1991) 2297–2301.
[76] S.M. Pincus, 近似熵(ApEn)作为一种复杂性测度 Chaos 5 (1) (1995) 110–117.
[77] K. Polat, S. Gunes, 采用一个基于树形判定分类法和快速傅立叶变换法的混合系统对癫痫的脑电信号进行分类,Appl. Math. Comput. 187 (2) (2007) 1017–1026.
[78] R.Q. Quiroga, J. Arnhold, K. Lehnertz, P. Grassberger, Kulback-Leibler和重整化熵:对癫痫患者脑电图的应用 Phys. Rev. E 42 (6) (2000) 8380–8386.
[79] A. Renyi, 熵与信息测度, Berkeley Symp. On Math. Statist. And Prob. Proc. Fourth Berkeley Symp. On Math. Statis. And Prob. 1 (1961) 547–561.
[80] J.S. Richman, J.R. Moorman, 基于近似熵和样本熵的生理时间序列分析, Am. J. Physiol. – Heart Circ. Physiol. 278 (2000) 2039–2049.
[81] M. Riedl, A. Müller, N. Wessel, 置换熵的实用性考虑, Eur. Phys. J. Spec. Top. 222 (2013) 249–262.
[82] P.S. Rodrigues, G.A. Giraldi, 计算Tsallis非广延局部图像分析法的Q指数,包含在:第22届巴西计算机图形学与图像处理专题讨论会,11–15th October 2009, Rio de Janiero, 2009, pp. 232– 237.
[83] O.A. Rosso, S. Blanco, J. Yordanova, V. Kolev, A. Figliola, M. Schurmann, E. Basar, 小波熵:短时电信号分析的一种新工具,J. Neurosci. Methods 105 (2001) 65–75.
[84] ROC – ROC曲线下面积。 <http://gim.unmc.edu/dxtests/roc3. htm> (访问日期 04.27.15).
[85] A.J.E. Seely, P.T. Macklem, 复杂系统与变异分析技术,Crit Care 8 (6) (2004) R367–R384.
[86] C.E. Shannon, 通信的数学理论, Bell Syst. Tech. J. 27 (3) (1948) 379–423.
[87] R. Sharma, R.B. Pachori, U.R. Acharya, 脑电信号自动识别中熵测度在本征模函数中的应用 , 熵17 (2015) 669–691.
[88] P.C. Shen, S.T. Liu, W.Z. Zhou, F.S. Lin, A.Y.Y. Lam, H.Y. Sung, W. Chen, J.W. Lin,M.J. Chiu, M.K. Pan, J.H. Kao, F. Lai, 基于生理学的多通道脑电图癫痫发作检测系统, PLoS ONE 8 (2013) e65862.
[89] Y. Song, P. Lio, 一种新的癫痫检测方法:基于样本熵的特征提取和极限学习机, J. Biomed. Sci. Eng. 3 (2010) 556-567.
[90] Y. Song, J. Crowcroft, J. Zhang, 基于优化样本熵和极端学习机的脑电图癫痫发作的自动检测, J. Neurosci. Methods 210 (2) (2012) 132–146. [91] G. Sonnino, G. Steinbrecher, A. Sonnino, Levy分布的Renyi熵,物理,AUC 23 (2013) 10–17.
[92] V. Srinivasan, C. Eswaran, N. Sriraam, 基于近似熵的癫痫脑电人工神经网络检测, IEEE Trans. Inform. Technol. Biomed. 11 (3) (2007) 288–295.
[93] A. Subasi, 基于小波特征提取与专家模型混合的信号分类, 专家系统. Appl. 32 (4) (2007) 1084–1093.
[94] B. Tellenbach, M. Burkhart, D. Sornette, T. Maillart, 香农延伸:用广义熵度量网络流量, in: S.B. Moon et al. (Eds.), PAM, LNCS, vol. 5448, Springer-Verlag, Berlin Heidelberg, 2009, pp. 239–248.
[95] N.V. Thakor, S. Tong, 脑电图定量分析方法的研究进展, Ann. Rev. 6 (2004) 453–495.
[96] S. Tong, A. Bezerianos, A. Malhotra, Y. Zhu, N. Thakor, 缺氧缺氧缺血性脑损伤后的脑电参数化熵分析, Phys. Lett. A 314 (5– 6) (2003) 354–361.
[97] S. Tong, N.V. Thakor, 定量脑电图分析方法及其在医学和生物学中的应用, 波士顿伦敦出版社 , 2009.
[98] A.T. Tzallas, M.G. Tsipouras, D.I. Fotiadis, 基于时频分析和人工神经网络的自动癫痫检测, Comput. Intell. Neurosci. 2007 (2007) 80510.
[99] A.T. Tzallas, M.G. Tsipouras, D.I. Fotiadis, 利用时频分析脑电图癫痫发作检测, IEEE Trans. Inf. Technol. Biomed. 13 (5) (2009) 703–710.
[100] E.D. Ubeyli, 基于小波系数的脑电信号分类联合神经网络模型, 数字,信号处理, 19 (2) (2009) 297–308.
[101] I. Veisi, N. Pariz, A. Karimpour, 利用排列熵快速检测噪声脑电信号中的癫痫,第七届IEEE生物信息学与生物工程国际会议论文集, 波士顿, MA, USA, 14–17 2007年10月, pp. 200–203.
[102] D. Wang, D. Miao, C. Xie, 基于最佳基小波包熵特征提取和分层脑电分类的癫痫检测, Expert Syst. Appl. 38 (2011) 14314–14320.
[103] WHO,世界卫生组织, 癫痫: 流行病学、病因学和预测, WHO Factsheet, 2001.
[104] WHO, 世界卫生组织, Epilepsy, 2012, URL: http://www.who. int/mediacentre/factsheets/fs999/en/.
[105] J. Xiang, C. Li, H. Li, C. Rui, B. Wang, X. Han, J. Chen, 基于模糊熵的癫痫发作信号检测,, J. Neurosci. Methods (2015), http:// dx.doi.org/10.1016/j.jneumeth.2015.01.015.
[106] Q. Yuan, W. Zhou, S. Li, D. Cai, 基于极端学习机和非线性特征的癫痫脑电分类, 癫痫研究. 96 (2011) 29–38.
[107] Y. Yuan, E.M. van Allen, L. Omberg, N. Wagle, A. Amin-Mansour, et al., 肿瘤基因组和蛋白质组数据在肿瘤类型中的临床应用价值, Nat. Biotechnol. 32 (2014) 644–652.
[108] M. Zanin, L. Zunino, O.A. Rosso, D. Papo, 排列熵及其在生物医学和物理学中的主要应用:概述,熵 14 (2012) 1553– 1577.
[109] J.P. Zbilut, C.L. Webber Jr., 递归图量化的嵌入和延迟, Phys. Lett. A 171 (3–4) (1992) 199–203.
[110] Z. Zhang, Y. Zhou, Z. Chen, S. Du, R. Huang,近似熵和支持向量机在脑电信号分类中的应用, Neural Regen. Res. 8 (20) (2013) 1844–1852. ,
基于知识的系统88(2015)85-96
内容列表详见ScienceDirect
基于知识的系统
期刊主页:www.elsevier.com/locate/knosys
熵在癫痫脑电信号自动诊断中的应用:综述
U. Rajendra Acharya a,b,c,* , H. Fujita d , Vidya K. Sudarshan a , Shreya Bhat e , Joel E.W. Koh a
*新加坡,义安理工学院,电子与计算机工程系
b新加坡,SIM大学,理工学院,生物医学工程系
c马来西亚,马来亚大学,工学院,生物医学工程系
d日本岩手,岩手县立大学(IPU),软件与信息科学学院
e印度,卡纳塔克邦,帕尔(576104),曼尼帕尔理工学院,生物医学工程系
文章信息
文章历史:
2015年3月23日收稿
2015年7月26日以修订形式收稿
2017年8月5日收录
2015年8月17日可在线查看
摘要:
癫痫是大脑的一种神经系统疾病,很难用脑电图(EEG)信号进行视觉诊断。因此,利用脑电信号进行癫痫的自动检测将成为医学领域的一个有用工具。采用如小波变换和熵的信号处理技术进行癫痫的自动检测可以优化系统的性能。目前,已开发出了许多算法,用来诊断脑电图信号中的癫痫发作。熵是反映脑电信号复杂程度的一个非线性参数。可以采用各种熵来区分正常、发作间期和发作期的脑电图信号。本文讨论了各种熵在癫痫脑电信号自动诊断中的应用。我们提出了区分正常、发作间期和发作期的脑电图信号的各种熵的独特范围,并按照此三类的辨识能力进行排列。这些熵可用于分类不同阶段的癫痫脑电信号,也可用于其他的生物医学应用。
©2015 Elsevier B.V 版权所有。保留所有权利。
关键词:
癫痫 发作间期 脑电图(EEG) 熵 模糊 HOS
作者通信地址:新加坡,义安理工学院,电子与计算机工程系,邮编599489 电话:+6564606135
电子邮件:aru@np.edu.sg (U.R. Acharya)
http://dx.doi.org/10.1016/j.knosys.2015.08.004
0950-7051/©2015 Elsevier B.V版权所有。保留所有权利。
目录
1. 引言 4
2. 材料和方法 6
2.1 使用的数据 6
2.2 熵选择与提取 8
2.2.1 Kolmogorov–Sinai熵(KSE) 9
2.2.2 近似熵(ApEn) 9
2.2.3 样本熵(SampEn) 10
2.2.4 谱熵(SEN) 10
2.2.5 Renyi熵(REN) 10
2.2.6 排列熵(PE) 11
2.2.7 Tsalli熵(TE) 11
2.2.8 模糊熵(FE) 12
2.2.9 小波熵(WE) 12
2.2.10 归一化双谱熵(S1,S2)和相熵(PhEn) 12
2.2.11 递归量化分析熵(RQAEn) 13
3. 熵特征的统计研究 14
4. 有关工作的讨论 15
4.1 两类:正常和癫痫发作信号 15
4.2 两类:发作间期(N或F类)和发作期(癫痫S)信号 16
4.3 三类:正常、发作间期(N或F)和发作期 17
4.4 五类:正常(两类),发作间期(两类)和发作期信号 20
5. 结论 20
参考文献 21
1. 引言
癫痫是一种常见的神经系统疾病,影响美国约300万人,影响全世界估计有5000万人[103,104]。癫痫的发病率和患病率约为世界人口的1-2% [67],在老年人口急剧增加。据估计,年龄在65岁及以上的老年人受这种病的影响达57万多例[104]。癫痫的特征是大脑皮层神经元异常和过度超同步化放电而引起的重复或短暂的知觉或行为紊乱。癫痫患者大脑经常会出现异常放电现象。癫痫的标志是经常无端发作,即癫痫发作[14]。根据世界卫生组织(WHO)的报告,癫痫是以反复发作为特征的,是对脑细胞异常的、通常是短暂的、不受控制的放电的物理反应[ 104 ]。根据临床表现,癫痫发作分为部分性或局灶性发作、全面性发作、单侧性发作和不能分类的发作[44,98,99 ]。局灶性癫痫发作仅涉及大脑半球的一部分,而全面性发作涉及整个大脑。任何年龄组的受试者都会受到癫痫发作的影响。
临床上要预测和诊断癫痫发作,需要通过含有癫痫标记的脑电信号来监测大脑活动。癫痫患者的脑电信号表现出两种状态:异常活动即发作间期或无癫痫发作(癫痫发作之间)和发作期(癫痫发作过程中)。发作间期脑电图信号为瞬态波形,呈尖峰或尖波。发作期脑电图信号为连续波形,呈棘波和尖波复合波[ 62 ]。一般来说,临床医生依靠识别癫痫发作间期(无癫痫发作)的脑电信号来进行预测,因为发作期的脑电信号很难获取。 因此,长程脑电图信号对于直观地监测和分析并定位癫痫患者得正常状态、发作间期和发作期是很有必要的。训练有素、经验丰富的神经生理学家可以采用传统的方法,通过长时间的脑电信号视觉检测将癫痫检测出来。这项工作是非常费时、乏味和主观的。因此,为了克服这些限制,可以使用计算机辅助检测癫痫脑电信号。
选择最能描述EEG信号行为的特征对于癫痫自动检测性能是很重要的。许多时域分析方法[63,64]、频域分析方法[26,38,93,1,77,21],时率分析方法[ 69 ],时频平面能量分布[35,98 ]、小波特征[ 38,2 ]和混沌特征如熵[ 106,64 ]被用来检测癫痫发作。在许多研究中,使用了两个或多个特征以及一个以上的分类器[66,100]。各种基于熵的措施已被用来量化和更好地了解癫痫发作期间和发作间之间差异的复杂性[20]。文献表明,熵具有利用计算机技术识别脑电信号中存在的复杂性的能力。 Acharya 等人[5–7] 通过不同的熵特征(近似熵、样本熵、相熵、香农熵、Renyi熵和HOS熵)来进行脑电图信号癫痫诊断。Sharma 等人[87]通过提取脑电图信号中的固有模态函数,使用香农熵、Renyi熵、近似熵和相熵分类了局灶性和非局灶性癫痫脑电信号, 准确率达87%。而据我们所知,这是第一篇描述大集合的熵进行脑电图信号癫痫诊断的文章。因此,在本文中,我们提出了各种熵的独特范围,即近似熵(ApEN)、模糊熵(FE)、样本熵(SampEn),Renyi 熵(RE)、谱熵(SEN),排列熵(PE),小波熵(SEN),Tsallis 熵(TE),高阶谱熵(S1,S2,PhEn),Kolmogorov–Sinai 熵(KSE)和递归量化分析熵(RQA En),应用在正常、发作间期和发作期的EEG信号。
图1给出了癫痫自动检测的框图。将脑电信号分为训练数据集和测试数据集,用于分类器的建立和性能评估。离线训练系统描述了建立脑电信号分类用的分类器所遵循的步骤。在脑电信号预处理之后,采用不同的熵算法对脑电信号进行特征提取。特征排序有助于根据其临床意义对特征进行排序,并提高分类器的性能。显著特征以及医生得出的脑电信号正常、发作期或发作间期参考数据可以用来训练分类器。在线系统中,可以从未分类的测试样本中提取特有特征,并使用所有的分类器参数来解决分类标签问题。分类器性能的准确性、敏感性、特异性和阳性预测值(PPV)得以评估。
              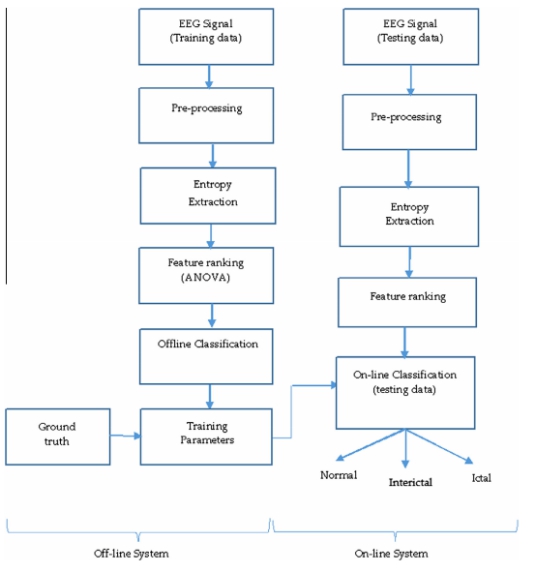
 图1 拟用方法框图 图1 拟用方法框图
2. 材料和方法
2.1 使用的数据
癫痫发作检测中测试不同熵效率的脑电图记录可以从波恩大学[11]的开放数据库中获取。所有的脑电图数据都没有任何人工制品。脑电数据可分为五个数据集。前两个数据集记录的是健康的志愿者睁眼和闭眼状态下的脑电信号,还有两个数据集记录的是癫痫病人发作间期的数据,第五个数据集括癫痫病人发作期的数据。因此,数据记录的两种分类处理了:(1)健康志愿者和癫痫发作病人和(2)癫痫发作间期和发作期病人。三种分类处理了正常、发作间期和发作期状态。五种分类处理了健康人闭眼、睁眼、癫痫患者发作间期(两类)和发作期。
EEG数据包共含有五个数据段(集合Z、O、N、F和S),记录了五名健康受试者清醒时闭眼(集合Z)和睁眼(集合O)以及癫痫病人术前评估的数据(两段发作间期和发作期),每个数据段长度均为23.6秒。在颅内深度植入电极来记录发作间期的时间间隔段,数据包括(1)相反大脑半球的海马体区数据(集合N),以及(2)致痫区数据(集合F)。植入大脑皮层的深度电极和带状电极被用来记录发作期段(集合E)。每个集合都选择了100个单通道数据段,包括健康人和癫痫病人(发作间期= 100,发作期=100)。每个EEG文件都包含4096个样品,并作为单独的脑电信号处理,产生共计300个脑电信号。在这项研究中,数据集O,F和S被用于进一步的分析。图2显示了三种典型的脑电信号。
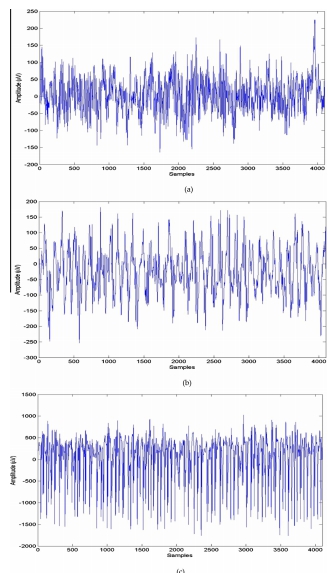
图2:典型的EEG信号:(a)正常;(b)发作间期;(c)发作期
2.2 熵选择与提取
在开发一种癫痫自动化检测系统时,需要提取能够更好地描述发作行为(静态或动态)的各种特征[97]。 本文基于各种熵分析方法评估区分了正常、发作间期和发作期的脑电信号。本节对脑电信号分类中使用的熵作了简要的描述。
熵是信息生成率的量度,它可用于信号处理中,以将有用信号与干扰噪声分离[ 54 ]。通常,高熵值对应于较高的不规则性或不可预测性,而低熵值对应于较高的正则性。熵是反映系统内混沌程度的非线性指标[ 54 ]。它经常被用来分析癫痫脑电信号,以检测是否有癫痫发作或检查癫痫发作的状态。熵参数大致分为谱熵和嵌入熵。从信号功率谱的幅值分量中计算得来的熵被成为谱熵,而直接使用时间序列计算得来的熵则被定义为嵌入熵[ 45,46 ]。
2.2.1 Kolmogorov–Sinai熵(KSE)
Kolmogorov–Sinai熵评估了信号的不确定度随着时间的变化[32],是从嵌入的时间序列信号中计算出来的[47]。它也被定义为非混沌信号的零度量熵。对于混沌信号来说,它的值大于零。Kolmogorov–Sinai熵是通过在相空间轨迹上找到彼此接近且与时间不相关的点来计算的。点对散度率产生了KSE值。tdiv为点对移动分开的平均时间。因此,KSE可从下列公式计算:

其中,KSE以每秒比特数表示。从嵌入空间重建系统轨迹将生成KSE值,如方程式(2)描述。
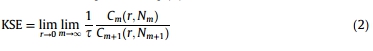
其中,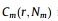 被称为一个相关函数,它给出了两点彼此接近的概率r。高KSE值表示高不可预测性。因此,KSE不能提供微小噪声信号的精确结果。 被称为一个相关函数,它给出了两点彼此接近的概率r。高KSE值表示高不可预测性。因此,KSE不能提供微小噪声信号的精确结果。
该熵的主要优点是,它有助于区分规则和混沌系统[ 65,31 ]。 当给定时间序列的长度变大时,它降低并衰减到零,这是该熵的主要限制[ 27 ]。
2.2.2 近似熵(ApEn)
近似熵用来评价信号变化的不稳定性[75,76]。它可以检测潜在情节行为的变化,并可通过模式长度(m)和相似系数(r)来比较样本的相似度。近似熵是一个尺度不变测度,因相似准则等价于数据的标准偏差。高度不规则的时间序列将得出高ApEn值,多个相似模式的时间序列则提供了低ApEn值。在数学上,ApEn的计算由下式得出:

其中,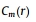 是长度m模式均值, 是长度m模式均值,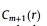 是长度m+1模式均值。模式均值是通过计算相似长度模式m和m+1的数量来计算的。在本研究中,我们选择m=2和r=0.2倍的EEG信号标准偏差[95,75]。 是长度m+1模式均值。模式均值是通过计算相似长度模式m和m+1的数量来计算的。在本研究中,我们选择m=2和r=0.2倍的EEG信号标准偏差[95,75]。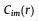 表示长度模式m的数量,由下式确定: 表示长度模式m的数量,由下式确定:

近似熵依赖于模式长度,而模式长度是不一致的,它通过计算与自身匹配的序列,避免产生ln(0)的结果。这种熵的优点是:(i)它可以计算相对段长度的噪声数据[ 85 ],(ii)它可以潜在地区分各种系统,如周期和多周期系统,混沌系统和随机系统[ 75 ],以及(iii)它可以给出比KS熵准确的统计结果[75]。
近似熵的缺点是:(i)它严重依赖于输入信号长度。特别是短信号产生比预期较低的值[80],(ii)该熵对于显著地噪音缺少意义[ 85 ],(iii)该熵是一个有偏差的统计,依赖于时间序列长度并需要计算与自身匹配的序列[ 76 ],以及(iv)一致性是不存在的,在很大程度上依赖于数据的长度。
2.2.3 样本熵(SampEn)
|



