n gate design”, Chinese Journal of Mechanical Engineering, 13(1), 14. Q. Shen and A. Chouchoulas, “FuREAP: A fuzzy-rough estimator of algae populations”, Artificial Intelligence in Engineering, 15, F. Shi, Z. L. Lou and Y. Q. Zhang, “An improved strategy for attribute reduction in rough set”, Sixth International Conference for Young Computer Scientists, 1, pp. 41–44, October 2001.
16. D. Dubois and H. Prade, “Rough fuzzy sets and fuzzy rough sets”, International Journal General Systems, 17, pp. 191–208, 1990.
17. L. P. Khoo, S. B. Tor and L. Y. Zhai, “A rough-set-based approach for classification and rule induction”, International Journal of Advanced Manufacturing Technology, 15, pp. 438–444, 1999.
18. L. P. Khoo, S. B. Tor and J. R. Li,
“A rough set approach to the ordering of basic events in a fault tree for fault diagnosis”, International Journal of Advanced Manufacturing Technology, 17,
19. R. S. Lee, Y. M. Chen and C. Z. Lee, “Development of a concurrent mold design system: a knowledge-based approach”, Computer Integrated Manufacturing Systems, 10(4), pp. 287– 307, 1997. 20. S. M. Chen, “A new method for constructing fuzzy decision trees and generating fuzzy classification rules from training examples”, Cybernetics and Systems: An International Journal, 31, pp. 763– 785, 2000. 21. P. S. Cracknell and R. W. Dyson, Handbook of Thermoplastics Injection Mould Design, Blackie Academic and Professional, 1993.
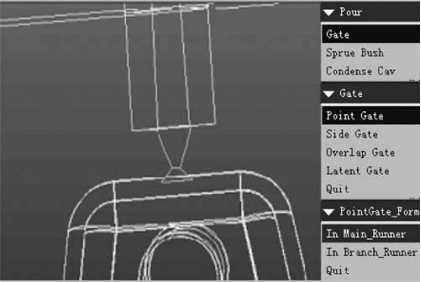
Fig. 5. The final design of point gate.
, An Improved Rough Set Approach to Design of Gating Scheme for Injection Moulding
F. Shi,1 Z. L. Lou,1 J. G. Lu2 and Y. Q. Zhang1 1Department of Plasticity Engineering, Shanghai Jiaotong University, P. R. China; and 2Center of CAD, Nanjing University of Chemical Technology, P. R. China
The gate is one of the most important functional structures in an injection mould, as it has a direct influence on the quality of the injection products. The design of a gating scheme includes the selectionof the types of gate and calculation of the sizes and determination of the location, which depends heavily on prior experience and knowledge and involves a trial-and-error process. Due to the vagueness and uncertainty in the design of a gating scheme, classical rough set theory is not effective. In this paper, a fuzzy rough set model is proposed, which is not based on equivalent relationships but on fuzzy similarity relationships. An inductive learning algorithm based on the fuzzy rough set model (FRILA) is then presented. Compared to decision tree algorithms, the proposed algorithm can generate fewer classification rules; moreover, the generated rules are more concise. Finally, an intelligent prototype system for the design of a gating scheme based on an induced fuzzy knowledge base is developed. An illustrative example proves the effectiveness of the proposed method.
Keywords: Fuzzy rough set; Gating scheme; Injection mold;
Intelligent design; Knowledge acquisition
1. Introduction
The manufacturing industry for plastic products has been growing rapidly in recent years, and plastics are used widely to substitute for metals. The injection moulding process is the most popular moulding process for making thermoplastic parts. The feeding system, which is one of the important functional structures, comprises a sprue, a primary runner, a secondary runner and a gate. The molten plastic flows from the machine nozzle through the sprue and runner system and into the cavities through the gate. Acting as the connection between the runner and the cavity, the gate can influence directly the mould venting, the occurrence of jetting, the location of weld lines, and warpage, shrinkage and residual stresses. Hence, the gate design is important for assuring the quality of the mould.
The design of a gate includes the selection of the type of gate, calculation of the size and determination of the location. And the design of a gate is based on the experience and knowledge of the designers. The determinations of the location and sizes are made based on a trial-and-error process. In recent years, a feature-modelling environment and intelligent technology have been introduced for gate design. Lee and Kim investigated gate locations using the evaluation criteria of warpage, weld lines and izod impact strength. A local search was used to determine the nodes of the location of the gate [1]. Saxena and Irani proposed a frame for a non-manifoldtopology-based environment. A prototype system for gate location design was developed. The criteria for evaluation were based on geometry-related parameters [2]. Lin selected the injection location and size of the gate as the major control parameters, and chose the product performance (deformation) as the optimising parameter. Combining the technologies of abductive networks and simulation annealing optimisation algorithms, the optimal model for the location and size of the gate was constructed [3,4]. Zhou et al. established a rule set for determining the location of the gate based on analysis of the plastic parts. The location of the gate was determined through reasoning with rules [5]. Pandelidis et al. developed a system which can optimise gate location based on the initial gating plans. The system used MOLDFLOW software for flow analysis, and controlled the temperature differential and the number of elements overpacked with an optimisation strategy [6].
Deng used ID3 and its modified algorithms to generate the rule set for the selection of the gate types [7]. However, there are many fuzzy or vague attributes in the selection of the types, such as the attribute of loss of pressure that has two fuzzy linguistic variables i.e. can be high and must be low. The ID3 algorithms cannot deal with fuzzy or “noise” information efficiently. It is also difficult to control the size of the decision tree extracted by the algorithms and sometimes very large trees are generated, making comprehensibility difficult [7,8].
Rough set theory provides a new mathematical approach to vague and uncertain data analysis [9,10]. This paper introduces the theory of rough sets for the design of a gating scheme. The selection of the type of gate is based on the theory of rough sets. Considering the limitations of rough sets, this paper proposes an improved approach based on rough set theory for the design of the gating scheme. The improved rough set approach to the scheme design will be given first. A fuzzy rough-set-based inductive learning algorithm (FRILA), which is applied in the improved approach, will then be presented. An example of the design of a gate will finally be given.
Table 1. Classification criteria.
|
Condition attributes
|
Fuzzy linguistic variables
|
|
Style of plastic parts (p)
|
(Deep, Middle, Shallow) Shell, (Deep, Middle, Shallow) Tube, (Deep, Middle, Shallow)
|
|
|
Ring
|
|
Number of cavities (n)
|
Single-cavity, Multi-cavity
|
|
Loss of pressure (l)
|
Can be high, Must be low
|
|
Condition of separating gate from parts (q)
|
Must be easy, Not request specially
|
|
Machining performance (m)
|
Must be easy, Not request specially
|
2. A Rough Set Approach to Gating Scheme Design
2.1 Design of the Gating Scheme
The model of the gating scheme design can be described as follows. A decision table with 4-tuples can be represented as T = (U, C, D, T). where U is the universe. C = {C1, C2, …, Ck} is the set of condition attributes, each of which measures some important feature of an object in the universe U. T(Ck) = { Tk 1,T2k ,...,TkSk} is the set of discrete linguistic terms. In other words, T(Ck)is the value set of the condition attributes. D = {D1, D2, …, Dl} is the set of decision attributes, that is, each object in the universe is classified by the set D.
Generally, the condition attributes can be classified as five sets, including style of plastic parts, number of cavities, loss of pressure, condition of separating gate from parts and machine performance. The details of the five condition attributes and corresponding variables of the fuzzy linguistic are shown in Table 1.
From the table, it can be seen that most of the attributes are vague since they represent a human perception and desire. For instance, shell, tube and ring are selected for the classification of plastic parts and their fuzzy linguistic values are “deep”, “middle” and “shallow”, respectively. For the attribute loss of pressure, “can be high” and “must be low” are selected to approximate the fuzzy attribute.
A fuzzy rule for gating scheme design can be written in the following form:
IF (C1 is T1 i1) AND … (Ck is Tik) THEN (DisDj) (1) where Tkik is the linguistic term of condition attribute Ck, and Dj is a class term of the decision attribute D.
Fuzzy rules with the form of Eq. (1) are used to perform min-max fuzzy inference. Let ck be the membership value of an object in Tk and d be the forecast value of Dj, where d = ik min(ck) and min is the minimum operator. If two or more rules have the sameconclusion, the conclusion with the largest value of d, which is also named the certainty factor is chosen.
For the problem of the gating schemedesign, a fuzzy design rule can be described as follows.
IF (Type of plastic part = middle shell)
AND (Number of cavities = single)
AND (Condition of separating gate from part = not request especially)(2)
THEN (Gating scheme = straight gate)
CF = 0.825
From the above rule, the gating scheme of the straight gate will be selected is s with a certainty factor of 0.825, if the type of part is middle shell and the number of cavities is single and the condition of separating gate from part is not required. The above is just like human language and is easy to understand.
2.2 Basic Concepts of Rough Sets
In recent years, the rough set (RS) theory, proposed by Pawlak, has been attracting the attention of the researchers. The basic idea of RS is to classify the objects of interest into similarity classes (equivalent classes) containing indiscernible objects via the analysis of attribute dependency and attribute reduction. The rule induction from the original data model is data-driven without any additional assumptions. Rough sets have been applied in medical diagnosis, pattern recognition, machine learning, and expert systems [10,11].
A decision table with a 4-tuple can be represented as T = <U, A, V, f>, where U is the universe, 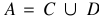 , C and D are the sets of condition and decision attributes, respectively, V is the value set of the attribute a in A, and f is an information function.
, C and D are the sets of condition and decision attributes, respectively, V is the value set of the attribute a in A, and f is an information function.
Assuming a subset of the set of attributes, two objects x and y in U are indiscernible with respect to P if and only if 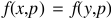 ,
, 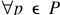 .The indiscernibility relation is written as IND(P). U/IND(P) is used to denote the partition of U given the indiscernibility relation IND(P).
.The indiscernibility relation is written as IND(P). U/IND(P) is used to denote the partition of U given the indiscernibility relation IND(P).
A rough set approximates traditional sets by a pair of sets, which are the lower and the upper approximations of the sets. The lower and upper approximations of a set Y . U given an equivalence relation IND(P) are defined as follows:
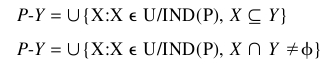
The definition of the lower approximation of a set involves an inclusion relation whereby the objects in an equivalence class of the attributes are entirely contained in the equivalence class for the decision category. This is the case of a perfect or unambiguous classification. For the upper approximation, the objects are possibly classified using the information in attribute set P.
Attribute reduction is important for rough set theory. Based on the above definitions, the concept of reduction, denoted by RED(P), is defined as follows: Q . P is a reduction of P if and only if IND(P)=IND(Q).
2.3 An Improved Rough Set Approach
In the design of the gating scheme, it is crucial to acquire the fuzzy rules efficiently. Knowledge acquisition is the bottleneck. A rough set is applied to solve the problem for the design of the gating scheme. The block diagram for the design of the gating scheme with the rough set is shown in Fig. 1. The case library is obtained from the experience and knowledge of experts and some reference books. A rough-set-based inductive learning algorithm is adopted to identify the hidden patterns and relationships in the case library and acquire knowledge.
The knowledge is represented as a set of fuzzy “if–Then” rules. During the design stage, the system employs the fuzzy rules to perform fuzzy inference according to the design requirements. Then the appropriate gating scheme can be obtained.
Although the rough set is efficient for knowledge acquisition, there are some limitations for the application of the original rough set in the selection of the gating scheme.
1. The original rough set is efficient for problems with discrete attributes, but it cannot deal with the fuzzy attributes efficiently. For fuzzy attributes, the traditional decision table is normally transformed into a binary table by obtaining Fig. 1. Block diagram of the gating scheme design with RS. the -cut set of the fuzzy set. Obviously, there is no crisp boundary between the fuzzy attributes.
2. The original rough set is based on the indiscernibility relation. The universe is classified into a set of equivalent classes with the indiscernibility relation. The lower and upper approximations are generated in terms of the equivalent classes. In practice, the original rough set classifies the knowledge too fussily, which leads to the complexity of the problem.
The fuzzy set and rough set theories are generalisations of classical set theory for modelling vagueness and uncertainty. Pawlak and Dubois proposed that the two theories were not competitive but complementary [11,16]. Both of the theories are usually applied to model different types of uncertainty. The rough set theory takes into consideration the indiscernibility between objects, whereas the fuzzy set theory deals with the ill-definition of the boundary of a class through the membership functions. The attributes can be presented by fuzzy variables, facilitating the modelling of the inherent uncertainty of the knowledge domain. It is possible to combine the two theories to solve the design problem of the gating scheme better.
A fuzzy rough set model is presented based on the extension of the classical rough set theory. The continuous attributes are fuzzified with the proper fuzzy membership functions. The indiscernibility relation is generalised to the fuzzy similarity relation. An inductive learning algorithm based on fuzzy rough set model (FRILA) is then proposed. The fuzzy design rules are extracted by the proposed FRILA. The gate design scheme is then obtained after fuzzy inference. The detailed implementation will be discussed in the next section.
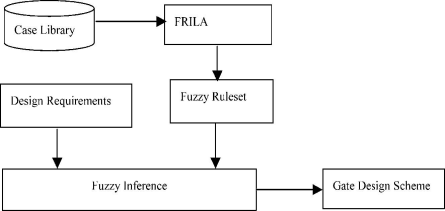
Fig. 1. Block diagram of the gating scheme design with RS.
3. Implementation of FRILA
A fuzzy rough-set-based inductive learning algorithm consists of three steps. These steps are the fuzzification of the attributes, attribute reduction based on the fuzzy similarity relation and fuzzy rule induction.
3.1 Fuzzifying the Attributes
Generally, there are some fuzzy attributes in the decision table, such as loss of pressure. These attributes should be fuzzified into linguistic terms, such as high, average and low. In other words, each attribute a is fuzzified into k linguistic values Ti, i = 1, …, k. The membership function of Ti can be subjectively assigned or transferred from numerical values by a membership function. A triangular membership function is shown in Fig. 2, where _x0007_(x) is membership value and x is attribute value. For instance, a shell part can be described as {0.8/deep, 0.4/middle, 0/shallow}. It should be mentioned that membership is not probability and the sum of the membership values may not equal 1. The concept of fuzzy distribution is given as follows. Assuming that attribute A has k linguistic terms whosemembership function is _x0007_Ai(x), respectively, where x is the value of A and i = 1, 2, …, k, the fuzzy distribution of A is 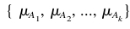 ,Rough Set Approach to Gating Scheme for Injection Moulding 665
,Rough Set Approach to Gating Scheme for Injection Moulding 665
Step 1. Calculate normal similarity relation matrix R.. in terms
of de.nition 3.
Step 2. Select 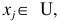 ,and let
,and let 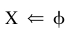 and
and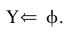 .
.
Step 3. 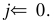
Step 4. If 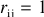 and
and 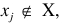 , then X . X . {xj}, Y . Y{xj}.;
, then X . X . {xj}, Y . Y{xj}.;
Step 5. 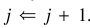 .
.
Step 6. If j < n, then GOTO Step 4; otherwise, GOTO next step.
Step 7. If card(Y) . 1, then 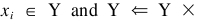 and {xi}, GOTO Step 3; otherwise,GOTO next step.
and {xi}, GOTO Step 3; otherwise,GOTO next step.
Step 8. Output the set X and let 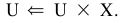
Step 9 If 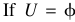 , then end; otherwise, GOTO Step 2.
, then end; otherwise, GOTO Step 2.
In step 7, card (Y) denotes the cardinality of set Y.
According to the algorithm, U/IND(R~ {.i}), the partition is calculated given the attribute ai . A with the level value .i. The partition of U given attribute set A with level value set can be de.ned as follows:
where A and . are the attribute set and the level value set, respectively, and operator . is de.ned as follows:
Considering a subset X C U and a fuzzy similarity relation R. de.ned on U, the lower approximation of X, denoted by R..(X), and the upper approximation of X, denoted by R. .(X), are respectively de.ned as follows:
Assuming U/IND(R. ) and Y are two partitions on U, where U/IND(R.) = {X1, X2, …, Xk} and Y = {Y1, Y2, …, Yr}, the positive region POS. C(Y)isde.ned as follows:.
The amount of data is normally very large and there is a lot of redundant information. Attribute reduction can remove the redundant or noise information successfully. In the attribute reduction, the attribute reduction set is not single. The cardi-nality of the reduction set determines the dimensionality of problem, so it is important to select a minimal reduction. The minimal reduction can be de.ned as follows:
Assuming a subset C′. C and C is the attribute set, C′ is the minimal reduction, if and only if C′ is characterised by following two properties.
In order to construct the fuzzy similarity relation, the measurement of the fuzzy similarity relation should be introduced first.
Generally, the max–min method, the relational factor method and the Minkowski distance-based closeness degree method are used to calculate the factor rij. Considering R. is a fuzzy similarity matrix and . is the level value, the matrix R. . is called normal similarity relation matrix after the following operation.
The matrix R has the properties of reflexivity and the symmetrivity. In order to obtain the partition of U given the fuzzy similarity relation R an algorithm is given as follows.
Input: fuzzy similarity matrix R. and level value . Output: U/IND(R), which is a partition of U given fuzzy similarity relation R. and level value.
Calculate normal similarity relation matrix R. in terms of definition 3.
Step 2. Select xj. U,and let X and Y.
Step 3. j. 0.
Step 4. If rij = 1 and xj .
X, then X . X . xj}, Y . Y{xj}.;
Step 5. j . j + 1.
Step 6. If j < n, then GOTO Step 4; otherwise, GOTO next step.
Step 7. If card(Y) . 1, then select xi . Y and Y . Y . {xi}, GOTO Step 3; otherwise, GOTO next step.
Step 8. Output the set X and let U . U . X. Step 9 If U = , then end; otherwise, GOTO Step 3.2
In step 7, card (Y) denotes the cardinality of set Y. {a}
According to the algorithm, U/IND(R~ {i}), the partition is calculated given the attribute ai . A with the level value i. The partition of U given attribute set A with level value set can be defined as follows: U/IND(R. A) =. {U/IND(R~ {{a} i}): ai . A, i . } (3) where A and . are the attribute set and the level value set, respectively, and operator . is defined as follows:
Considering a subset X C U and a fuzzy similarity relation .AR. defined on U, the lower approximation of X, denoted by (X), and the upper approximation of X, denoted by R. (X), are respectively defined as follows: .
(X) = {Y:Y. U/IND(R), Y . X) (5) .A .AR(X) = {Y:Y. U/IND(R), Y . X (6) CAssuming U/IND(R) and Y are two partitions on U, where .CU/IND(R) = {X1, X2, …, Xk} and Y = {Y1, Y2, …, Yr}, the positive region POS.
The amount of data is normally very large and there is a lot of redundant information. Attribute reduction can remove the redundant or noise information successfully. In the attribute reduction, the attribute reduction set is not single. The cardinality of the reduction set determines the dimensionality of problem, so it is important to select a minimal reduction. The minimal reduction can be defined as follows:
Assuming a subset C′. C and C is the attribute set, C′ is the minimal reduction, if and only if C′ is characterised by following two properties:
Assuming a condition attribute set C and a decision attribute set D, the degree of dependency of C on D, denoted by where card(X) denotes the cardinality of set X and 0 . According to the definition of the degree of dependency, the attribute significance for every attribute a . C . R can be defined as follows.
In order to obtain the minimal reduction, a hierarchy attribute reduction algorithm is proposed as follows. Step 2. Compute the attribute significance SIG(x, R, D) for Step 3. Select the attribute x with the highest value SIG.
The computational complexity of the algorithm is O(m2), where m is the number of the algorithm,attribute reduction can be treated as a tree traversal. Each node of the tree represents the condition attribute Calculating the minimal reduction can be transformed to picking the best based on some heuristic information. The operator can reduce the computation by using refrom .
3.3 Fuzzy Rules Induction
Based on the above fuzzy rough set model, the rule inductive learning algorithm is proposed, and is described as follows.
1. Fuzzify the attributes and compute the fuzzy distribution of them.
2. Calculate the fuzzy similarity matrix for every attribute.
3. Calculate the fuzzy partition U/IND(R. ) given the fuzzy similarity relation R. with the value set . based on Algorithm 1.
4. Calculate the minimal attribute reduction based on Algorithm
5. Calculate the attribute core of the condition attribute with respect to the decision attribute and obtain the minimal reduction of the condition attribute, then delete the redundant objects.
6. For every object, calculate the value core of the condition attribute, and then delete the redundant attribute values and objects.
7. Delete the same objects in decision table and translate the decision rules.
4. A Case Study
In order to evaluate the effectiveness of the proposed method, an example shown in Fig. 3 is chosen in this section. The design requirements are given as follows:
Part style: middle shell
Number of cavities: single Loss of pressure: may be high Condition of separating gate from parts: must be easy Machining performance: must be easy Part material: ABS
4.1 Fuzzy Knowledge Acquisition Eliciting knowledge from any source of data is notoriously difficult, so knowledge acquisition is a bottleneck. There are five condition attributes for the gating scheme design as shown in Table 1. The attribute number of cavities has no fuzziness for its value is either “single” or “multiple”, so it is represented as {0, 1}, and the other four attributes are fuzzy ones and are represented by membership functions. The decision attribute of the gating scheme has nine linguistic terms, which correspond to nine gating schemes, respectively. First, a fuzzy decision table including 144 objects is constructed by calculating the fuzzy distributions of each attribute. Second, The fuzzy similarity relations of six attributes are constructed in terms of the Euclid distance based closeness degree. Then given the level values, the fuzzy similarity matrix is transformed to a normal similarity matrix. Third, the fuzzy partition U/IND(R)is calculated in terms of Algorithm 1 given the fuzzy similarity relation R. with the value set . where the level values of the condition attributes are as follows: the one of decision attribute, denoted .
Fig. 3. An example part.
Rough Set Approach to Gating Scheme for Injection Moulding 667 by d, is 0.8. Fourth, Calculate the attribute reduction so there is no redundant attribute. Finally, 22 fuzzy rules with the form of Eq. (2) are obtained.
According to the different level values, the different number of fuzzy rules can be obtained. In practice, it is shown that the value of d has the largest effect on the number of rules.
If the level values of condition attributes are given as follows: the value of d and the number of rules (num) is obtained, and shown in Fig. 4.
4.2 Discussion
As stated previously, the different number of fuzzy rules can be obtained in terms of the level values. In reference [7], the D3 algorithm and ID3-like algorithms are used to extract rules. However, the algorithms tend to involve more attributes than FRILA for the hierarchical structure of its output decision rules. In other words, the rules induced by the ID3-like algorithms have redundant attributes and are not more concise than the rules induced by FRILA. In the gating scheme design, on one hand, more concise and fewer rules lead to a more efficient selection of gate; on the other hand, more rules with higher level values lead to a higher selection accuracy. These two factors have to be traded off to satisfy application-dependent specifications. The comparison of ID3-like algorithms and FRILA is shown as Table 2, where the algorithms of MNIDR and MNID are improved versions of classical ID3 in reference [7].
It is seen from Table 2 that higher . may lead to a bigger rule set with higher accuracy rate; moreover, when the accuracy rate is 100%, the number of rules induced by FRILA is fewer than that induced by ID3-like algorithms. Therefore, FRILA can induce fewer fuzzy rules with different level knowledge to cover the field and reduce the possibility of combination explosion.
4.3 Design Implementation
With the rule set for gating scheme design incorporated in an integrated environment, a prototype intelligent gating scheme design system has been developed. A commercial CAD system, named Pro/Engineering, is selected as the software platform, and Visual C++ language and Pro/Toolkit are selected as the developing tools. The prototype system can implement the
Table 2. Comparison of four algorithms.
Algorithm Number of rules Accuracy (num) rate (%) ID3 70 100 MNIDR 60 100 MNID 49 100 FRILA: automatic design of the gate. The prototype system employs the induced rules to perform fuzzy inference. For each datum to be classified, all rules are applied. Based on the fuzzy classification model described in Section 2, the following rule is selected:
IF (Number of cavities = single) AND (Loss of pressure = may be high) AND(Condition of separating gate from parts = must be easy) THEN (Gating scheme = point gate) CF = 0.93
Therefore, a point gate is suitable for the part. The sizes of the gate are designed using the reference manuals, for instance, point gates vary in size from diameters of 0.8–2 mm for unloaded materials to diameters of 2.5–3 mm for loaded grades [21]. In order to facilitate the automation of the gating design, a gate feature library is provided, which contains nine types of classical gates. Modifications of gate features can be done by changing the key shape parameters. According to the designer’s choice, the gate feature is then added to the plastic part through assembly operations, such as mating, aligning and orienting. The gate is finally designed as shown in Fig. 5.
Fig. 4. Relation between d and num. Fig. 5. The final design of point gate.
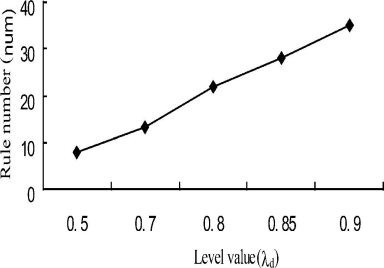
Fig. 4. Relation between �d and num
5. Conclusions
In the design of a gate, the design of a gating scheme relies heavily on the knowledge and experience of the mold engineer and involves a trial-and-error process. In this paper, the design of a gating scheme is discussed in detail. Due to the vagueness and uncertainty in the selection of the gate, the classical rough set theory is not effective. By combining a fuzzy set with a rough set, a fuzzy rough-set-based inductive learning algorithm is proposed. Using the algorithm, the fuzzy rule set for the selection of a gate is established. Compared to the decision tree algorithms, the proposed algorithm can generate fewer classification rules and the generated rules are more concise. An intelligent gating scheme design prototype system based on the gating scheme knowledge base is developed, which can improve the efficiency of the gate design.
Acknowledgement
The paper is partly supported by National Natural Science Foundation of P. R. China (No. 60175019) and the Youth Foundation of Science, Shanghai, P. R. China.
References
1. B. H. Lee and B. H. Kim, “Optimization of part wall thickness to reduce warpage of injection-molded parts based on the modified complex method”, Polymer Plastics Technology Engineering, 34, pp. 793–811, 1995.
2. Saxena and R. K. Irani, “An integrated NMT-based CAE environment-part : Application to automated gating plan synthesis for injection molding”, Engineering with Computers, 9, pp. 220– 230, 1993.
3. Lin, “Optimum gate design of freeform injection mould using the abductive network”, International Journal of Advanced Manufacturing Technology, 17, pp. 297–304, 2001.
4. C. C. Tai and J. C. Lin, “The optimal position for the injection gate of a die-casting die”, Journal of Materials Processing Technology, 86, pp. 87–100, 1999.
5. Z. Y. Zhou, Z. Zh. Gu and J. Y. Shi, Research on integrated design techniques for injection mold runner system”, Journal of Computer-Aided Design and Computer Graphics, 12(1), pp. 6–10, 2000 (in Chinese).
6. I. Pandelidis, Q. Zou and T. J. Lingard, “Optimization of gate location and operational molding conditions for injection molding”, Proceedings ANTEC, 46, pp. 18–20, 1988.
7. Q. Deng, “The key technologies in mold intelligent manufacture”, Shanghai Jiaotong University, Shanghai, 1996 (in Chinese).
8. J. Wang, J. Cui and K. Zhao, “Investigation on AQ11, ID3 and the principle of discernibility matrix”, Journal of Computer Science and Technology, 16(1), pp. 1–12, 2001. 9. Y. Yuan and M. J. Shaw, Induction of fuzzy decision trees”, Fuzzy Sets and Systems, 69(2), pp. 125–139, 1995.
10. Z. Pawlak, “AI and intelligent industrial applications: the rough set perspective”, Cybernetics and Systems: An International Journal, 31(4), pp. 227–252, 2000.
11. Z. Pawlak, “Rough sets and fuzzy sets”, Fuzzy Sets and Systems, 17(1), pp. 88–102, 1985. 12. R. Slowinski and D. Vanderpooten, “A generalized definition of rough approximations based on similarity”, IEEE Transactions on Knowledge and Data Engineering, 12(2), pp. 331–336, 2000.
13. Z. L. Lou and Y. Q. Zhang, “Fuzzy knowledge acquisition i



