一种关于粗糙集改进注射模具浇道的报告

浇道在注塑模具中是一个很重要的功能结构，因为它可以直接影响注塑产品的质量。设计的浇注方案包括开模类别的选择，计算尺寸，和定位的判断，这些都大大的依赖与长期的经验和知识，也包括大量的试验过程。为了应付在开模过程中模糊的和一些不定因素，经典的而是一个模糊的近似关系。理论还是不够的。在这篇论文中，一个模糊粗糙集的模型被计划，这不是依靠等量的关系，而是一个模糊的近似关系。一种归纳学习算法基于模糊粗糙集模型（ frila ）被呈现。与决策体系运算法则相较，那被提议的运算法则能产生较少的分类法则，而且，被产生的规则更简洁。最后，一个智能的为浇注设计的原型系统基于一个感应模糊知识库被发展。举一个例子来证明被提议方法的效力。

关键词：模糊粗糙集;浇注计划;注塑模; 智能设计;获取知识

1. 注射

近几年来塑料产品的制造工业一直在快速的增加，塑料广泛地用来替换金属。注射模具程序被广泛的用于分离可塑性物质的模制程序。进给系统是一个重要的功能结构，包含一个注料口，一个主流道，副流道和一个内浇道。融化的塑料从机器喷嘴内流出经过注料口和流道系统，然后进入内浇道型腔。当流道和型腔连接运到时，内浇道能直接地作用模具排气，射出，使焊接使焊接的位置发生翘曲，收缩和产生剩余的压迫力。因此，内浇道的设计对保证模具的质量很重要。

内浇道的设计包括其类型的选择 ，尺寸的计算和位置的定位。而且内浇道的设计以经验和设计者的知识为基础，位置的定位和尺寸的确定是建立在一个大量实验的基础上的。在最近几年，在浇道的设计上功能建模环境和智能化技术已经实施。Lee和Kim调查研究了内浇道的位置确定，并对其翘曲，焊接线和挤入冲击力量进行了标准评估。本地搜索被用来确定

浇道的节点位置。saxena和irani提出了一个框架，一个非manifoldtopology - 基于环境。一个原型系统为浇道口位置的计划。评价的标准分别为基于地理相关参数[ 2 ] 。林选择了注入位置和浇道口的大小作为主要的控制参数，而且选择产品表面（变形）当作优化参数。联合溯网络技术和模拟韧性最佳化运算法则，来构造内浇道的位置和大小的最佳

模型【3，4】。Zhou等人建立了一个规则来确定内浇道塑料部分的位置。内浇道塑料位置的确定是依据规则【5】。Pa ndelidis等人开发了可以优化浇口位置的基础上初步浇注计划制度。

系统用MOLDFLOW软件作为流程分析，而且控制了温度差别和元素o Verpacked的数字用最佳化策略【6】。

Deng用了ID3和它被修正的运算法则所产生的规则来设定内浇道的选择类型【7】。有许多模糊或含糊的属性在选择类型中，比如压力的损失的属性有两种模糊的语言学变数也就是可能是高的而且一定是低。ID3运算法则不能有效率的处理模糊或“噪音”数据。控制尺寸的大小也很困难，被运算法则吸取的系统和有时非常大的系统被产生，使理解成为困难[7,8].

粗糙集提供了一个新的数学的方式来达成对含糊又不确定的数据分析【9，10】。本文介绍粗集理论来设计一个浇注计划。这篇文章计划以粗糙集为基础进行改良来作为内浇道模具的设计。改进粗糙集办法的方案设计会获得第一。一个模糊的粗糙集以归纳学问运算法则(FRILA)为基础，在改良的方法中应用，然后将被呈现。内浇道的一个例子将会在最后出现。

2.粗糙集改进注射模具的设计

2.1注塑浇道的设计

注塑浇道的模具设计描述如下。决策表配有4元组可派代表作为T=《U 、 C 、 D,T》，其中U代表总值。c = （ C1组， C2 ， … ，对照）是一套条件属性，其中每一项措施的一些重要特点是一个物体在U中，T（CK）={TK1,TK2…TKSK}。是一组不连续的语言学期限。换句话说，T(CK)是价值组的特征D={D1 ， D2, …, Dl}是决定属性的组，也就是说，每个物体都被固定在D分类中。一般情况下，条件属性可分为五套，其中包括风格的塑料零件，有多少个模腔，其损失压力，条件相分离的闸门，从零部件和机器表现。详情五个条件属性相应的变量的模糊语言在表1中显示。从表中可以看出，大部分的属性是空泛的，因为它们代表了人类感知和欲望。例如，壳牌，管和环获选分类塑胶零件和模糊语言的价值观分别为"深层次" ， "中等"和"浅"。压力亏损属性在近似的模糊属性中可高可低。

一种浇注方案的模糊规则设计可以写成如下形式：

粗糙集的内浇道设计的663塑料模具方案。

如果（C1是T1i1）及（Ck是T ik)…..然后（D是Dj）（1），Tkik是情况属性CK的语言学期限，和Dj是决定属性D的一个班级期限。

模糊的规则与形式的情商。（ 1 ）用来演出极大极小模糊推理。ck是全体成员价值，在Tki的一个物体k和d是Dj的预测价值，d=最小（Ck）和最小是最小的操作员。如果二或更多规则有相同的结论，结论用最大的d，也叫做确定因素评价被选择。

对于注塑内浇道设计的问题，一个模糊的规则描述如下。如果（塑料部分的类型=中央去壳）及（型腔数量=单独的）及（分开的情况来自部分内浇道口=不特别请求）（2）然后（注塑浇道=直浇道）比照= 0.825

从以上的规定在浇注计划的直浇道所选定的是s与必然的因素0.825.如果类型的部分是中间壳体和单独的型腔数目，这种情况的浇道分离是不被要求的。以上仅仅是像人类的语言，并且容易明白。

2.2 粗糙集的基本概念

近年来，由Pawlak提出的粗糙集理论，已经引起了研究者的注意，RS的基本构思阐述了归类物体的相似性（同等性）其中载有indiscernible物体经分析有属性的依赖性并且属性在减少。该规则归纳法是由原来的数据驱动的，无需任何额外的假设。粗糙集已适用于医疗的诊断，模式识别，机器学习和专家系统【10，11】。

决策表由4个元组可以表现为T = <u, a, v, f> ，其中U是总值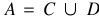，   D, C和D是集的条件和决策属性，v是值集的属性a在A中，f是一个信息功能。

假设的一个子集的属性，p包含于A，在U中的两个物体x和y是indiscernible当且仅当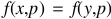, 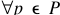. 不可分辨关系被写作IND（P）。U/IND(P)是用来分割

给出的不可分辨关系的U。

粗糙集近似于传统的双组集，这是降低和逼近上面的集。定义如下：

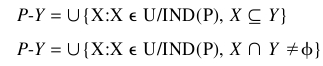
组的较低的近似值的定义包括一个包含关系那里在一个同等中的物体属性的班级完全地被包含在同等为决定种类分类。这是一个完美或不含糊的情形分类。对于上面的近似值，物体可能被分类使用归于P中。

属性减少，是重要的粗集理论。基于对上述定义，概念的减少，记红色（ P ）的定义如下：

Q包含于P，P是减少的，当且仅当IND(P)=IND(Q)

2.3. 一种改进的粗糙集方法

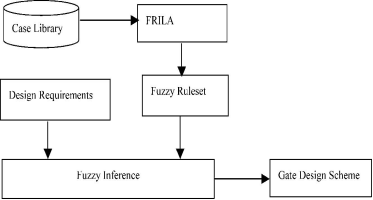
在设计浇注计划，关键是要有效率的掌握模糊规则。知识的获取是瓶颈。粗糙集适用于解决浇注计划的问题。框图，为设计的浇注计划与粗糙集显示在图1。可以从专家和一些参考书籍上获取经验和知识。粗略设定为基础的感应式学习算法是通过找出隐藏模式和关系案来获取知识。知识是派一组模糊"如果-那么" 规则。在设计阶段，该系统采用了模糊规则，以履行模糊推理按照这个设计要求。然后适当的浇注计划，可获得的。

虽然粗糙集是一种有效的获取知识的途径，但是还是有一些限制在选择原有的浇注计划上。

1．原始粗糙集能够有效的处理离散属性，但它不能有效的处理模糊属性。作为模糊属性，传统的决策表通常转化为一个二进制表所获取-截集的模糊集。显然，在模糊属性之间不存在脆化边界。

2. 原始粗糙集是建立在不可分辨的关系上的。总值被分为相等的关系在不可分辨的关系中。高的和低的属性近似产生而言相当于同等关系。在实践中，原来的粗糙集分类知识太繁琐，从而导致了问题的复杂性。

模糊集和粗糙集理论是以偏概全了古典集合论模型的模糊性和不确定性。Pawlak和Dubois提出了这两个理论不互相排斥的，而是互补的【11，16】。这两个理论通常适用于不同类型模型的不确定性。粗糙集理论考虑了不同物体之间，而模糊理论处理了隶属函数边界的错误定义。该属性可以由模糊变量表现，有利于该造型的不确定性知识领域。为了将浇注计划问题设计的更好，有可能将两者合二为一。

这种模糊粗糙集模型是建立在经典的模糊粗糙集上的。连续属性是模糊化具有适当的模糊隶属函数。该不可分辨关系，是以偏概全了模糊的相似性关系。一种归纳学习算法基于模糊粗糙
集模型（ frila ） 被提议。模糊规则的设计是在提取拟议frila之后。浇道的设计计划是在得到了模糊推论之后。详细的实施将在下节讨论。

3. 实施frila

基于一种模糊粗糙集归纳学习算法构成3个步骤。这些模糊属性的步骤是建立在模糊相似关系和模糊规则的建立上的。

3.1 模糊属性

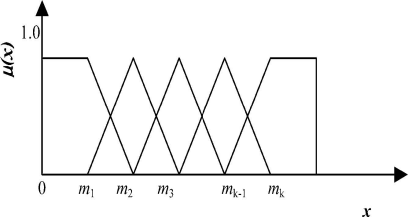
一般来说，在决策表中有一些模糊的属性，例如压力的亏损。这些属性应该模糊到语言的条件上来,如:高,平均及低.换言之,i = 1, …, k. … …调隶属函数的钛可以主观转让或转移，数值功能是由会员制定的.三角形隶属函数显示如图.

2. 在那里,(x)的会集值和x的属性值.举例来说,一个客体的一部分,可以说是（ 0.8/deep ， 0.4/middle ， 0/shallow ） 。值得一提的是成员的概率是不确定的,总的价值也可能不等于1.概率模糊化的分布如下.

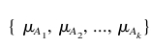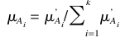假设属性A有K的语言学而言,他的隶属函数就是Ai(x),分别的,X是A的价值, i = 1, 2, …, k,A的模糊分配是,其中根据该定义，模糊分布情况壳体部分代表作为（ 0.67 ， 0.33 ， 0 ） 。

3.2 属性基于模糊相似关系

经典的定义上,低的和高的属性引进参考的不确定关系,被假定为一种等价关系(自反,对称,传递).在实践中,不可分辨关系可以延长到一个模糊相似关系.

考虑到U = {u1, u2, …, un}的总值,模糊相似关系R˜ __n_在总值中被称为模糊相似矩阵,如果每个元素rij有以下两个属性:

自反: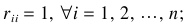    对称: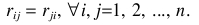   为了构建模糊相似关系，应先测量该模糊相似关系.一般情况下,采用极大极小方法，对关联系数法与Minkowski基于距离贴近度法是用来计算因子rij 。

考虑到R是一个模糊相似矩阵,是水平值时, 矩阵R 〜就是所谓正常的相似关系矩阵
经过以下操作。

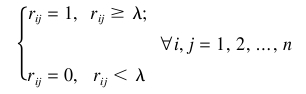
该矩阵R 〜有特性的自反性和symmetrivity 。 为了获得分割铀鉴于模糊相似关系R 〜 ，给出了算法如下。

算法一
输入：模糊相似矩阵R 〜和水平的价值。输出： / ind （ 〜 ） ，这是一个分区铀给模糊相似关系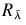和水平的价值。

粗糙集改进注塑浇注成型计划665.

第1步。计算正常相似关系矩阵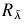而言定义3 。
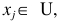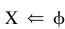第2步。选择的，和设和 。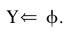
第3步。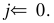
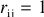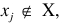第4步。如果和，则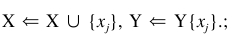
第5步。 。
第6步。如果j < N ，则转到第4步，否则，直接到下一步骤。
第7步。如果卡（ y ）的1 ，然后选择喜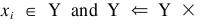 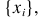跳至第3步，否则，直接到下一步骤。
第八步。输出设置X和设。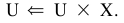
第九步，如果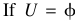，然后结束，否则，跳至第2步。
在第七步，卡（ y ）的指基数集.

根据该算法, 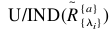就是分割计算鉴于属性A和水平值_i..U的部分给予属性集A的水平集在以下被定义.

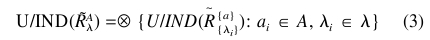其中A和_是属性集和水平价值集,分别的,管理定义如下:

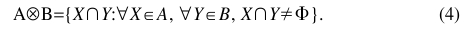考虑的一个子集xcu和模糊相似关系R˜定义U,下属性X,被定义为R˜A__(X),上属性的X,被定义为R˜(X),分别定义如下:

假设/ ind （ 〜 c ）和Y两种分割对U ，那里/ ind （ 〜
c ） = （象X1 ， x2 ， … ，空间XK ）和Y = （ y1 ， Y2型， … ， 54 ） ， 积极地区名次（ y ）的定义如下：

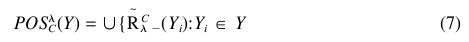该数据量通常非常大，并有一大量的冗余信息。减少属性可以成功的移除多余的噪音信息.属性的减少,属性集不是单独的, 基数根据削减订定的维度问题，所以这是很重要的,最起码的减少,可以定义如下:

假设一个子集C′_ C,C是属性集,C是最低限度的减少,当且仅当C的特点有以下两个属性:

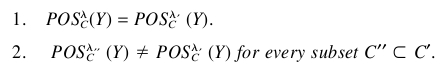假设条件属性集C和决策属性定d时，C对D的依赖程度,定义如下:

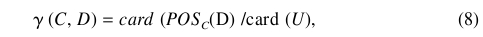卡（ x ）的指基数的集x和0小于等于Y, (C,D) _ 1666 F. Shi et al.

根据该定义的依赖程度，每一个属性的a _ C _ R意义可以被定义如下:

SIG(a, R, D) =  (R _ {a}, D) _  (R, D) (9)

为了取得最低限度的减少，提出了等级属性运算法,由如下提出.

算法2

输入：决策表中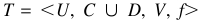

输出：最小的减少属性设定为R。

第1步，让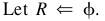

第2步，计算属性的指示的SIG(x, R, D)作为每一个属性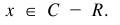

第3步，选择的属性X作为最高价值SIG(x, R,D)让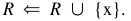

第4步，如果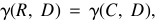然后GOTO第5步骤；另外GOTO第2步骤，第5步骤，归还R。

3．3  模糊规则归纳法

基于在模糊粗糙模型的规则上，规则inductivelearning被应用，描述如下。

1． 属性的模糊和计算他们的模糊特性。

2． 对每个属性进行类似模糊点阵计算。

3． 计算模糊分割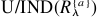所提供懂得模糊类似关系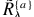和建立在Algorithm 1.的价值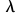集。

4． 计算以 Algor 为基础的最小的属性减少 2.

5． 计算属性的核心属性情况，获得情况属性的特征，然后划除脆性化的物体。

6． 对于每个物体，计算物体的核心价值，然后化除对于的物体属性。

7． 在决策表中化除相同的物体，并且翻译决定规则。

4．一个案件研究

为了评估被提议方法的效力。在图3中选择一个区段的一个例子来说明。设计的需求在下面被描述：

部分风格：              中间壳体

型腔的数目：            独立的

压力的损失 ：           可能高的

部分浇道的分离情况 ：   一定容易

机器表面：              一定容易

材料部分：              ABS

4．1 模糊知识的获得

众所周知从任何数据来源获取知识是很困难的，因此，知识的获得是一个瓶颈。有5个浇道的情况属性如表1所示。型腔数量的独立和倍数属性在价值上没有模糊性，而且另外四个属性是模糊的。浇道方安的决定属性有九个语言学期限，分别的。首先，模糊决策表包含144个由模糊分配的每个属性的物体。其次模糊simi larity的六个属性的关系根据Euclid构造的以距离为基础的近似程度。然后给出水平价值，模糊类似点阵被转换为一个正常的类似点阵。第三，模糊分割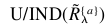根据被提供模糊类似关系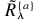来运算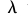，集的属性情况的水平价值由如下给出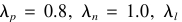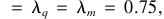：而且被指示的决定属性之一被定义为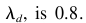第四，计算属性的减少，因此，没有多余的属性。最后， 22个模糊以情绪商数的形式规定 (2) 被获得。

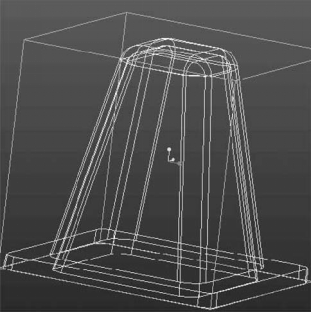
依照不同的水平价值，不同的模糊规则的数量能被获得。 在练习中，一般显示了规则数量价值的最大效果。水平属性的评价如下显示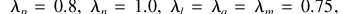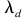：的价值关系和规则的数量

NUM）被获得，在表4中被显示。

4.2  讨论

在先前的阐述中，不同数量的模糊规则可以获得相应的水平价值。在参考[7]中，ID3的运算法则和像3一样的规则被作为精确的规则。然而，运算法则包含的属性比FRILA的阶层结构包含的多。换句话说，在浇道的设计中，更简洁和更少的规则使得浇道的选择更有效率。在另一方面，跟国的规则和更高层的价值观导致了较大的选择精确性。这两个因素都要能够方便的转换，以满足依赖型的规格。比较的ID3样算法和frila表现为表2中，mnidrand mnid算法是经典中的改进版本ID3的修改[7]。它被认为是从表2中，较大的可能会导致更大的规则集，具有较高的准确率;

此外，当准确率是百分之一百时，有很多的FRILA规则少于ID3的运算法则。因此，frila能引起更少模糊规则的不同层次的知识涵盖领域，并减少可能的组合失败。

4.2  设计的实施

浇道设计的粗糙集放安已经被纳入一个综合的环境，一种原型智能浇注方案设计系统已经研制成功。商业CAD系统，命名为Pro/Engineering是被选定为软件平台，Visual C + +语言和Pro /工具包是选定为开发工具等。该原型系统可以实现浇道的自动设计。原型系统采

用诱导规则，以执行模糊推理。每个基准面繁荣划分，所有的规则都是适用的。基于模糊分类阳离子模型在2中被描述，下列规则被选择：

如果（型腔的数目=单独的）和（压力的损失=可能高）和（浇道的分离情况=一定简单）最后（浇道计划=浇道点）CF = 0.93

因此，一个浇道点是适合的部分。浇道的尺寸采用了参考手册来设计的，例如，浇道点的尺寸不等，从直径0.8 - 2毫米，以直径为2.5-3毫米，为负载等级[ 21 ] 。为了便于浇道自动化的设计，由浇道的特征库提供了9种古典浇道。改变关键形状参数可以浇道的特征。根据设计者的选择，浇道的特点是，添加到塑料零件经过装配作业，如交配，对准和定向，最终设计如图5所示。

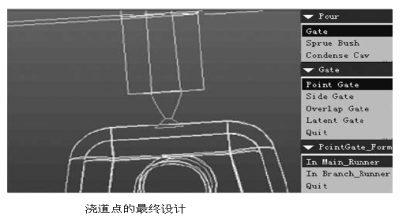
图5 浇道点的最终设计