
| 我们提供全套毕业设计和毕业论文服务,联系微信号:biyezuopinvvp QQ:1015083682 |
| 储油罐的变位识别与罐容表标定 |
| 文章来源:www.biyezuopin.vip 发布者:毕业作品网站
|
|
|
47.49
|
3.37%
|
2866.2
|
2966.2
|
100.00
|
3.37%
|
|
1412
|
1461.2
|
49.24
|
3.37%
|
2816.2
|
2914.4
|
98.23
|
3.37%
|
|
1462
|
1513.0
|
50.98
|
3.37%
|
2766.2
|
2862.7
|
96.50
|
3.37%
|
|
1512
|
1564.7
|
52.74
|
3.37%
|
2716.2
|
2811.0
|
94.76
|
3.37%
|
|
1562
|
1616.5
|
54.49
|
3.37%
|
2666.2
|
2759.2
|
93.02
|
3.37%
|
|
1612
|
1668.2
|
56.24
|
3.37%
|
2616.2
|
2707.5
|
91.26
|
3.37%
|
|
1662
|
1720.0
|
57.98
|
3.37%
|
2566.2
|
2655.7
|
89.51
|
3.37%
|
|
1712
|
1771.7
|
59.73
|
3.37%
|
2516.2
|
2603.9
|
87.76
|
3.37%
|
|
1762
|
1823.5
|
61.46
|
3.37%
|
2466.2
|
2552.2
|
86.03
|
3.37%
|
|
1812
|
1875.2
|
63.19
|
3.37%
|
2416.2
|
2500.5
|
84.30
|
3.37%
|
|
1862
|
1927.0
|
64.95
|
3.37%
|
2366.2
|
2448.7
|
82.53
|
3.37%
|
|
1912
|
1978.7
|
66.68
|
3.37%
|
2316.2
|
2397.0
|
80.80
|
3.37%
|
|
1962
|
2030.4
|
68.43
|
3.37%
|
2266.2
|
2345.3
|
79.07
|
3.37%
|
|
2012
|
2082.2
|
70.20
|
3.37%
|
2216.2
|
2293.5
|
77.32
|
3.37%
|
|
2062
|
2134.0
|
71.95
|
3.37%
|
2166.2
|
2241.7
|
75.55
|
3.37%
|
|
2112
|
2185.7
|
73.67
|
3.37%
|
2116.2
|
2190.0
|
73.84
|
3.37%
|
|
2162
|
2237.4
|
75.43
|
3.37%
|
2066.2
|
2138.3
|
72.08
|
3.37%
|
|
2212
|
2289.2
|
77.16
|
3.37%
|
2016.2
|
2086.5
|
70.32
|
3.37%
|
|
2262
|
2340.9
|
78.89
|
3.37%
|
1966.2
|
2034.8
|
68.60
|
3.37%
|
|
2312
|
2392.7
|
80.67
|
3.37%
|
1916.2
|
1983.0
|
66.85
|
3.37%
|
|
2315.8
|
2396.6
|
80.78
|
3.37%
|
1866.2
|
1931.3
|
65.12
|
3.37%
|
|
2365.8
|
2448.4
|
82.54
|
3.37%
|
1816.2
|
1879.5
|
63.35
|
3.37%
|
|
2367.1
|
2449.6
|
82.56
|
3.37%
|
1766.2
|
1827.8
|
61.61
|
3.37%
|
|
2417.1
|
2501.4
|
84.34
|
3.37%
|
1716.2
|
1776.1
|
59.88
|
3.37%
|
|
2467.1
|
2553.1
|
86.05
|
3.37%
|
1666.2
|
1724.3
|
58.12
|
3.37%
|
|
2517.1
|
2604.9
|
87.82
|
3.37%
|
1616.2
|
1672.6
|
56.37
|
3.37%
|
|
2567.1
|
2656.6
|
89.53
|
3.37%
|
1566.2
|
1620.8
|
54.64
|
3.37%
|
|
2617.1
|
2708.3
|
91.28
|
3.37%
|
1516.2
|
1569.1
|
52.87
|
3.37%
|
|
2667
|
2760.0
|
93.03
|
3.37%
|
1466.2
|
1517.3
|
51.14
|
3.37%
|
|
2668.8
|
2761.9
|
93.11
|
3.37%
|
1416.2
|
1465.6
|
49.42
|
3.37%
|
|
2718.8
|
2813.7
|
94.83
|
3.37%
|
1366.2
|
1413.8
|
47.65
|
3.37%
|
|
2768.8
|
2865.4
|
96.59
|
3.37%
|
1316.2
|
1362.1
|
45.91
|
3.37%
|
|
2818.8
|
2917.2
|
98.34
|
3.37%
|
1266.2
|
1310.4
|
44.18
|
3.37%
|
|
2868.8
|
2968.9
|
100.09
|
3.37%
|
1216.2
|
1258.6
|
42.42
|
3.37%
|
|
2918.8
|
3020.7
|
101.84
|
3.37%
|
1166.2
|
1206.9
|
40.68
|
3.37%
|
|
2968.8
|
3072.4
|
103.58
|
3.37%
|
1116.2
|
1155.1
|
38.94
|
3.37%
|
|
3018.8
|
3124.1
|
105.31
|
3.37%
|
1066.2
|
1103.4
|
37.19
|
3.37%
|
|
3068.8
|
3175.9
|
107.06
|
3.37%
|
1016.2
|
1051.6
|
35.43
|
3.37%
|
|
3118.8
|
3227.6
|
108.80
|
3.37%
|
966.2
|
999.9
|
33.71
|
3.37%
|
|
3168.8
|
3279.4
|
110.55
|
3.37%
|
916.2
|
948.2
|
31.96
|
3.37%
|
|
3168.9
|
3279.5
|
110.55
|
3.37%
|
866.2
|
896.4
|
30.20
|
3.37%
|
|
3218.9
|
3331.2
|
112.27
|
3.37%
|
816.2
|
844.6
|
28.45
|
3.37%
|
|
3268.9
|
3382.9
|
114.03
|
3.37%
|
766.2
|
792.9
|
26.71
|
3.37%
|
|
3318.9
|
3434.7
|
115.76
|
3.37%
|
716.2
|
741.2
|
24.99
|
3.37%
|
|
3368.9
|
3486.4
|
117.52
|
3.37%
|
666.2
|
689.4
|
23.25
|
3.37%
|
|
3418.9
|
3538.2
|
119.26
|
3.37%
|
616.2
|
637.7
|
21.51
|
3.37%
|
|
3468.9
|
3589.9
|
121.01
|
3.37%
|
566.2
|
585.9
|
19.74
|
3.37%
|
|
3518.9
|
3641.7
|
122.76
|
3.37%
|
516.2
|
534.2
|
18.02
|
3.37%
|
|
3568.9
|
3693.4
|
124.51
|
3.37%
|
466.2
|
482.5
|
16.28
|
3.37%
|
|
3618.9
|
3745.1
|
126.23
|
3.37%
|
416.2
|
430.7
|
14.50
|
3.37%
|
|
3668.9
|
3796.9
|
127.98
|
3.37%
|
366.2
|
379.0
|
12.77
|
3.37%
|
|
3718.9
|
3848.6
|
129.74
|
3.37%
|
316.2
|
327.2
|
11.02
|
3.37%
|
|
3768.9
|
3900.4
|
131.48
|
3.37%
|
266.2
|
275.5
|
9.28
|
3.37%
|
|
3818.9
|
3952.1
|
133.23
|
3.37%
|
|
|
|
|
|
3868.9
|
4003.9
|
134.95
|
3.37%
|
|
|
|
|
|
3918.9
|
4055.6
|
136.70
|
3.37%
|
|
|
|
|
|
3968.9
|
4107.4
|
138.45
|
3.37%
|
|
|
|
|
由上述的表格可以得出相对误差稳定,不会随高度发生变化。
当储油罐体发生变位时 ,我们就油面及油浮子的位置与倾斜角度的变化情况分成将该问题三类,然后就每一类进行分析,找出了储油罐中油的体积与油浮子位置的函数关系,其立体图如图4-4所示: ,我们就油面及油浮子的位置与倾斜角度的变化情况分成将该问题三类,然后就每一类进行分析,找出了储油罐中油的体积与油浮子位置的函数关系,其立体图如图4-4所示:
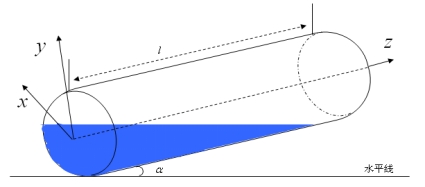
图4- 4
(1)当油浮子的高度在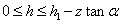 时,如图4-5所示,截面图如图4-6所示 时,如图4-5所示,截面图如图4-6所示
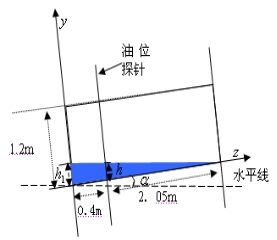 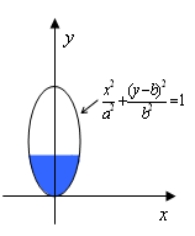
图4- 5 图4- 6截面图
截面面积为:

所以油罐体积为:
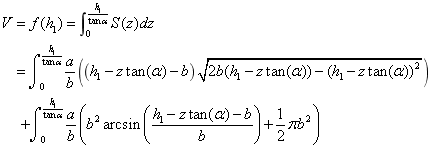 (1.1) (1.1)
将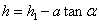 代入公式(1.1) 代入公式(1.1)
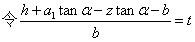 ,则公式(1.1) ,则公式(1.1)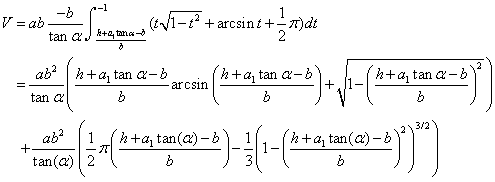
(2)当油浮子的高度在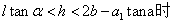 ,如图4-7所示, ,如图4-7所示,
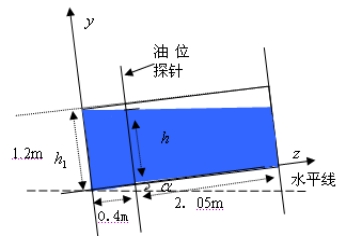
图4- 7
截面面积为:
 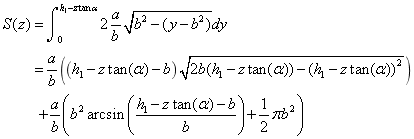
所以油罐装油的体积为;
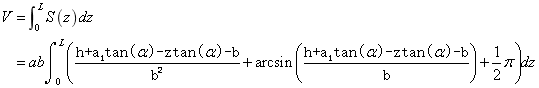
将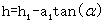 公式, 公式,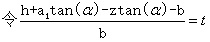
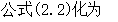 : :
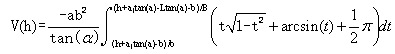
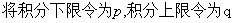 ,则 ,则
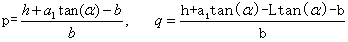
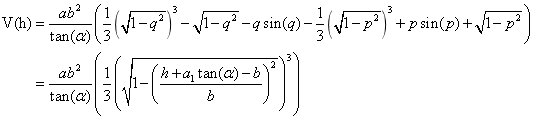 (3)当油浮子的高度 (3)当油浮子的高度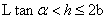 时,如图4-8所示, 时,如图4-8所示,
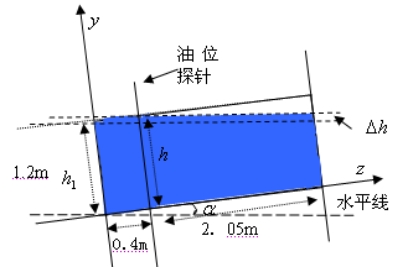
图4- 8
其中,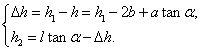 ,此时截面面积为: ,此时截面面积为:
 所以油罐装油的体积为 所以油罐装油的体积为
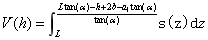
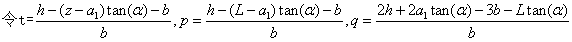 则上式公式变为: 则上式公式变为:
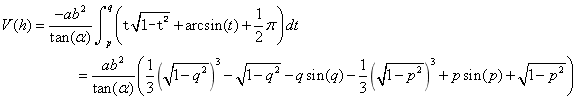
利用Matlab中的命令subs代人附件1实验数据中的各高度得到储油罐中的理论油量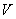 。 。
由附件1实验数据中进油量、出油量及储油罐罐内油量初值可以得到储油罐中的实际油量,根据理论油量及实际油量就可以得出误差。
由附录中的程序youliang2,我们得到了理论油量,误差及相对误差。
倾斜时进油后理论储油量与实际储油量随高度的变化规律如图4-9所示:
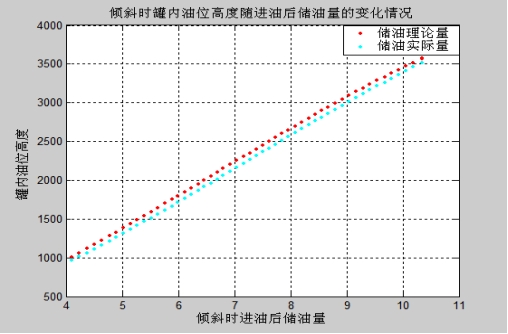
图4- 9
倾斜时出油后理论储油量与实际储油量随高度的变化规律如图4-10所示:
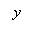 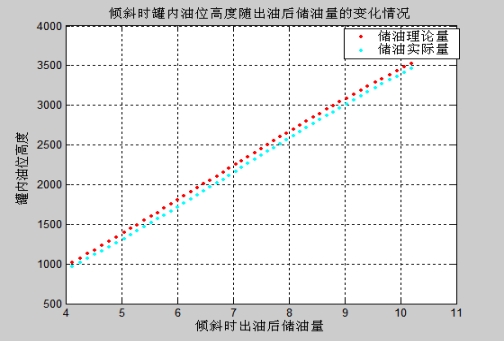
图4- 10
将倾斜进油和倾斜变位出油的储油理论值和储油实际值及误差和相对误差的数据如表4-2所示:
表4- 2
|
倾斜变位进油
|
倾斜变位出油
|
|
储油量实际量
|
储油量理论值
|
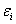 (误差) (误差)
|
相对误差
|
储油量实际值
|
储油量理论值
|
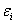 (误差) (误差)
|
相对误差
|
|
962.9
|
1010.0
|
7.19
|
4.67%
|
3464.7
|
3523.1
|
58.37
|
1.66%
|
|
1012.9
|
1058.3
|
45.47
|
4.30%
|
3414.7
|
3478.1
|
63.35
|
1.82%
|
|
1062.9
|
1118.0
|
55.19
|
4.94%
|
3364.7
|
3430.4
|
65.67
|
1.91%
|
|
1112.9
|
1167.5
|
54.67
|
4.68%
|
3314.7
|
3382.0
|
67.28
|
1.99%
|
|
1162.9
|
1222.1
|
59.29
|
4.85%
|
3264.7
|
3330.9
|
66.19
|
1.99%
|
|
1212.9
|
1279.2
|
66.34
|
5.19%
|
3214.7
|
3289.4
|
74.69
|
2.27%
|
|
1262.9
|
1327.5
|
64.63
|
4.87%
|
3164.7
|
3234.5
|
69.77
|
2.16%
|
|
1312.8
|
1382.6
|
69.82
|
5.05%
|
3114.7
|
3188.9
|
74.17
|
2.33%
|
|
1362.8
|
1433.6
|
70.81
|
4.94%
|
3064.7
|
3137.3
|
72.57
|
2.31%
|
|
1412.7
|
1485.0
|
72.23
|
4.86%
|
3014.7
|
3088.9
|
74.11
|
2.40%
|
|
1462.7
|
1536.1
|
73.35
|
4.78%
|
2964.7
|
3040.1
|
75.40
|
2.48%
|
|
1512.7
|
1591.9
|
79.14
|
4.97%
|
2914.7
|
2989.2
|
74.48
|
2.49%
|
|
1562.7
|
1645.1
|
82.42
|
5.01%
|
2864.7
|
2947.7
|
82.98
|
2.82%
|
|
1612.7
|
1697.4
|
84.67
|
4.99%
|
2814.7
|
2891.1
|
76.36
|
2.64%
|
|
1662.7
|
1749.9
|
87.16
|
4.98%
|
2764.7
|
2845.4
|
80.62
|
2.83%
|
|
1712.7
|
1796.6
|
83.89
|
4.67%
|
2714.7
|
2794.0
|
79.31
|
2.84%
|
|
1762.7
|
1848.8
|
86.08
|
4.66%
|
2664.7
|
2747.5
|
82.72
|
3.01%
|
|
1812.7
|
1900.0
|
87.32
|
4.60%
|
2614.7
|
2695.8
|
81.07
|
3.01%
|
|
1862.7
|
1952.7
|
90.01
|
4.61%
|
2564.7
|
2644.5
|
79.78
|
3.02%
|
|
1912.7
|
1999.2
|
86.48
|
4.33%
|
2514.7
|
2598.1
|
83.33
|
3.21%
|
|
1962.7
|
2052.7
|
89.97
|
4.38%
|
2464.7
|
2547.1
|
82.38
|
3.23%
|
|
2012.7
|
2103.2
|
90.50
|
4.30%
|
2414.7
|
2500.2
|
85.47
|
3.42%
|
|
2062.7
|
2148.4
|
85.72
|
3.99%
|
2364.7
|
2451.9
|
87.11
|
3.55%
|
|
2112.7
|
2202.3
|
89.54
|
4.07%
|
2314.7
|
2402.9
|
88.14
|
3.67%
|
|
2162.7
|
2252.7
|
90.01
|
4.00%
|
2264.7
|
2349.7
|
84.97
|
3.62%
|
|
2212.7
|
2303.7
|
91.01
|
3.95%
|
2214.7
|
2298.8
|
84.11
|
3.66%
|
|
2262.7
|
2352.2
|
89.44
|
3.80%
|
2164.7
|
2256.0
|
91.29
|
4.05%
|
|
2312.7
|
2402.7
|
90.02
|
3.75%
|
2114.7
|
2204.4
|
89.66
|
4.07%
|
|
2362.7
|
2452.2
|
89.51
|
3.65%
|
2064.7
|
2156.6
|
91.83
|
4.26%
|
|
2412.7
|
2497.9
|
85.17
|
3.41%
|
2014.7
|
2106.7
|
91.97
|
4.37%
|
|
2462.7
|
2548.7
|
85.93
|
3.37%
|
1964.7
|
2053.1
|
88.35
|
4.30%
|
|
2512.7
|
2599.6
|
86.83
|
3.34%
|
1914.7
|
2005.6
|
90.81
|
4.53%
|
|
2562.7
|
2644.7
|
81.96
|
3.10%
|
1864.7
|
1953.5
|
88.78
|
4.54%
|
|
2612.7
|
2696.3
|
83.55
|
3.10%
|
1814.7
|
1905.1
|
90.39
|
4.74%
|
|
2662.7
|
2748.8
|
86.11
|
3.13%
|
1764.7
|
1852.8
|
88.02
|
4.75%
|
|
2712.7
|
2798.9
|
86.14
|
3.08%
|
1714.7
|
1801.5
|
86.77
|
4.82%
|
|
2762.7
|
2847.2
|
84.49
|
2.97%
|
1664.7
|
1752.7
|
87.99
|
5.02%
|
|
2812.7
|
2895.9
|
83.13
|
2.87%
|
1614.7
|
1699.3
|
84.55
|
4.98%
|
|
2862.7
|
2942.1
|
79.34
|
2.70%
|
1564.7
|
1645.9
|
81.18
|
4.93%
|
|
2912.7
|
2992.6
|
79.84
|
2.67%
|
1514.7
|
1602.0
|
87.27
|
5.45%
|
|
2962.7
|
3044.2
|
81.48
|
2.68%
|
1464.7
|
1544.1
|
79.35
|
5.14%
|
|
3012.7
|
3089.6
|
76.91
|
2.49%
|
1414.7
|
1492.6
|
77.89
|
5.22%
|
|
3062.7
|
3140.8
|
78.10
|
2.49%
|
1364.7
|
1444.1
|
79.41
|
5.50%
|
|
3112.7
|
3189.7
|
76.99
|
2.41%
|
1314.7
|
1392.3
|
77.56
|
5.57%
|
|
3162.7
|
3234.0
|
71.32
|
2.21%
|
1264.7
|
1333.4
|
68.62
|
5.15%
|
|
3212.7
|
3284.1
|
71.39
|
2.17%
|
1214.7
|
1280.5
|
65.78
|
5.14%
|
|
3262.7
|
3334.6
|
71.88
|
2.16%
|
1164.7
|
1230.6
|
65.91
|
5.36%
|
|
3312.7
|
3379.0
|
66.29
|
1.96%
|
1114.7
|
1175.1
|
60.37
|
5.14%
|
|
3362.7
|
3423.5
|
60.82
|
1.78%
|
1064.7
|
1124.7
|
59.97
|
5.33%
|
|
3412.7
|
3473.2
|
60.46
|
1.74%
|
1014.7
|
1067.8
|
53.10
|
4.97%
|
|
3462.7
|
3517.7
|
54.93
|
1.56%
|
964.7
|
1011.8
|
47.05
|
4.65%
|
|
3512.7
|
3569.5
|
56.73
|
1.59%
|
|
|
|
|
|
3514.7
|
3573.2
|
58.49
|
1.64%
|
|
|
|
|
由上述的程序还可以描绘出倾斜时储油量的误差随罐内油位高度的变化情况,如图4-11所示:
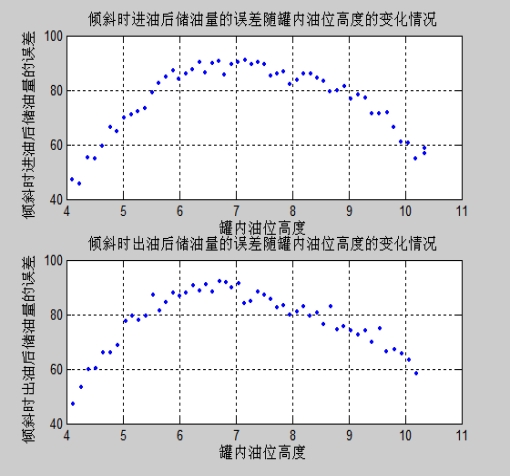
图4- 11
由上述图我们可以知道倾斜时不管是进油后储油量的误差还是出油后储油量的误差均随罐内油位高度的变化呈正态分布,说明该模型建立得贴合实际。
由上述得到储油罐发生变位时体积关于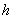 的公式我们可以给出罐体变位后油位高度间隔为1cm的罐容表标定值(即进/出油量与罐内油位高度的表格),如表4-3所示: 的公式我们可以给出罐体变位后油位高度间隔为1cm的罐容表标定值(即进/出油量与罐内油位高度的表格),如表4-3所示:
表4- 3罐体变位后油位高度间隔为1cm的罐容表标定值
|
高度(h)
cm
|
体积(v)
L
|
高度(h)
cm
|
体积(v)
L
|
高度(h)
cm
|
体积(v)
L
|
高度(h)
cm
|
体积(v)
L
|
|
1
|
3.531
|
26
|
461.5
|
51
|
1413.9
|
76
|
2491.3
|
|
2
|
6.2635
|
27
|
494
|
52
|
1456
|
77
|
2534
|
|
3
|
9.9748
|
28
|
527.1
|
53
|
1498.4
|
78
|
2576.6
|
|
4
|
14.7563
|
29
|
560.9
|
54
|
1540.9
|
79
|
2619.1
|
|
5
|
20.6908
|
30
|
595.2
|
55
|
1583.5
|
80
|
2661.4
|
|
6
|
27.8542
|
31
|
630.1
|
56
|
1626.3
|
81
|
2703.6
|
|
7
|
36.3163
|
32
|
665.6
|
57
|
1669.2
|
82
|
2745.5
|
|
8
|
46.1424
|
33
|
701.5
|
58
|
1712.2
|
83
|
2787.2
|
|
9
|
57.3935
|
34
|
738
|
59
|
1755.3
|
84
|
2828.7
|
|
10
|
70.127
|
35
|
774.9
|
60
|
1798.5
|
85
|
2870
|
|
11
|
84.3968
|
36
|
812.2
|
61
|
1841.8
|
86
|
2911.1
|
|
12
|
100.2541
|
37
|
850
|
62
|
1885.1
|
87
|
2951.8
|
|
13
|
117.7475
|
38
|
888.2
|
63
|
1928.5
|
88
|
2992.3
|
|
14
|
136.923
|
39
|
926.7
|
64
|
1971.9
|
89
|
3032.5
|
|
15
|
157.8246
|
40
|
965.7
|
65
|
2015.4
|
90
|
3072.4
|
|
16
|
180.4939
|
41
|
100.5
|
66
|
2058.8
|
91
|
3112
|
|
17
|
204.971
|
42
|
1044.6
|
67
|
2102.3
|
92
|
3151.2
|
|
18
|
228.9
|
43
|
1084.5
|
68
|
2145.7
|
93
|
3190.1
|
|
19
|
254.9
|
44
|
11248
|
69
|
2189.1
|
94
|
3228.6
|
|
20
|
281.9
|
45
|
1165.3
|
70
|
2232.5
|
95
|
3266.7
|
|
21
|
309.8
|
46
|
1206.2
|
71
|
2275.8
|
96
|
3304.4
|
|
22
|
338.5
|
47
|
1247.2
|
72
|
2319.1
|
97
|
3341.7
|
|
23
|
368.1
|
48
|
1.2886
|
73
|
2362.3
|
98
|
3378.5
|
|
24
|
398.5
|
49
|
1330.1
|
74
|
2405.4
|
99
|
3414.9
|
|
25
|
429.7
|
50
|
1371.9
|
75
|
2448.4
|
100
|
3450.7
|
问题二
我们一开始考虑当储油罐水平放置时油量与浮油子高度的函数关系。
当储油罐水平放置无横向与纵向倾斜时,设油高为h,所建立的空间直角建立坐标系如图4-12所示:
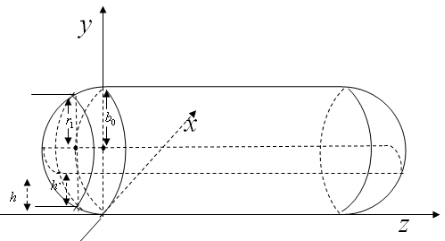
图4- 12
储油罐中储油的体积可分为两部分,圆柱体中储存油的体积与两端的球罐体中油的体积,根据对称性,两端的球罐体中油的体积相等。用垂直于z轴 的平面截储油罐,根据截面法求体积公式可求出储油的体积。
第一种情况: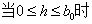
1、对于圆柱体部分: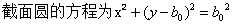
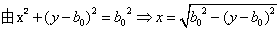
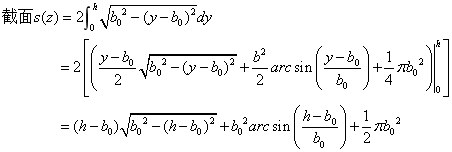
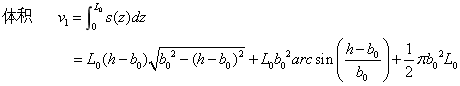
2、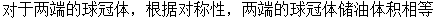 ,如图4-13所示: ,如图4-13所示:
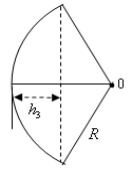 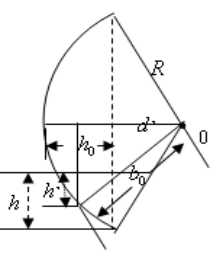
图4- 13 图4- 14
由图4-13可看出,根据几何关系:
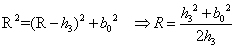
用平面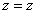 截球罐体,设截得小圆半径为 截球罐体,设截得小圆半径为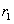 ,所图4-14所示,根据几何关系得: ,所图4-14所示,根据几何关系得:
 
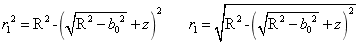
截面圆的油高为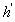 , ,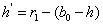
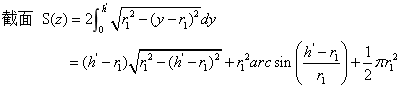
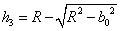

积分解得:
 
第二种情况: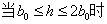
对于圆柱体的部分同第一种情况
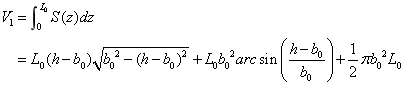
对于球罐体体积
截面圆的油高为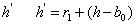

这种情况与第一种情况相同,因此与第一种情况相同。
模型的建立:
V与h的函数关系为:

我们就油所占的体积进行初步讨论,建立笛卡尔坐标系如图4-15,可以得出球冠体的球面方程为:
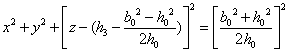
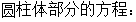 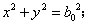
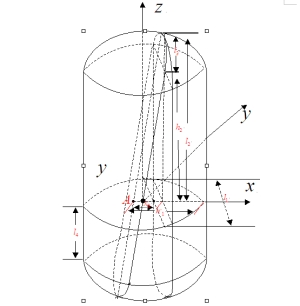
图4- 15
如图4-15所示,油罐体中所含油的部分分成两份,分别计算它们的体积。
因为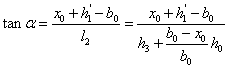
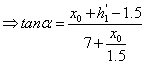
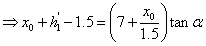
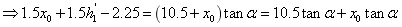
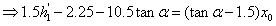
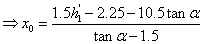
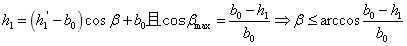
右半部分的体积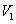 利用投影法可以由以下约束公式算出 利用投影法可以由以下约束公式算出
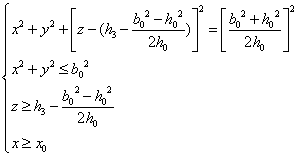
由上述第一个公式可以得出曲顶柱体的盖面方程为
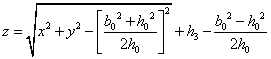
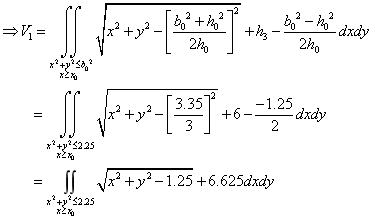
左半部分的体积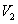 近似利用截面法可以由以下公式算出,由图4-15可以得出 近似利用截面法可以由以下公式算出,由图4-15可以得出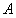 点的坐标为 点的坐标为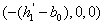 ;过垂直于 ;过垂直于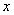 轴做截面,设过 轴做截面,设过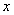 的截面面积为 的截面面积为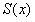 ; ;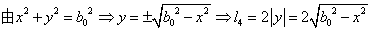
由图4-15可知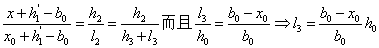
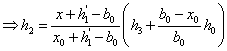
过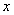 的截面面积为 的截面面积为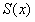 近似可表示如下: 近似可表示如下:
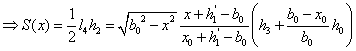
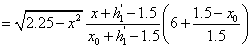
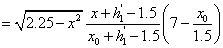
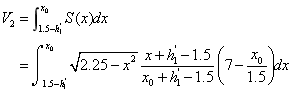
有上述的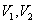 可以得到储油罐中油量与油位高度及变位参数的函数关系: 可以得到储油罐中油量与油位高度及变位参数的函数关系:
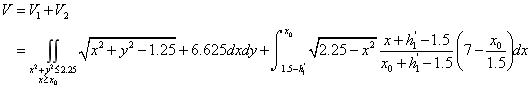
以下为在固定的横向偏转角度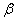 条件下,就纵向倾斜角度 条件下,就纵向倾斜角度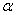 的变化进行分类讨论。 的变化进行分类讨论。
令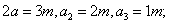
情形Ⅰ.当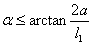 时, 时,
(1)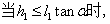 该情况的图4-16所示: 该情况的图4-16所示:
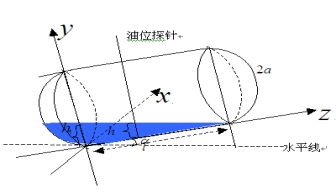
图4- 16
由图4-16可知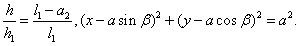

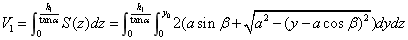


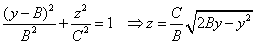
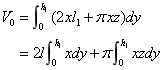
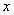 和 和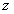 式代入 式代入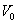 式,得: 式,得:


由此可得:
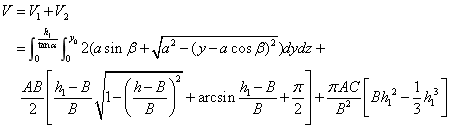
(2)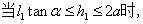 该情况如图4-17所示: 该情况如图4-17所示:
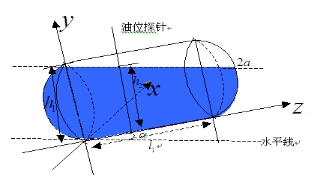
图4- 17
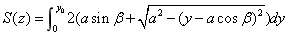
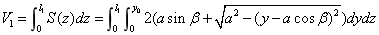
同上可得
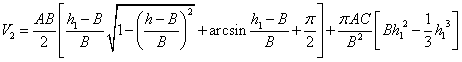
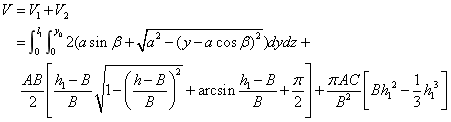
(3)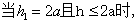 该情况如图4-18所示: 该情况如图4-18所示:
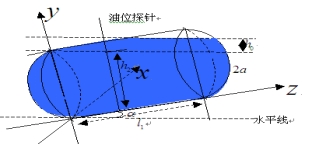
图4- 18
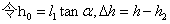
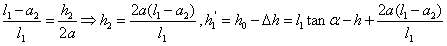
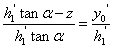 , ,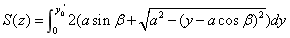
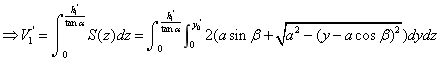
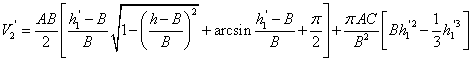
设实际储油罐总体积为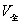 , ,
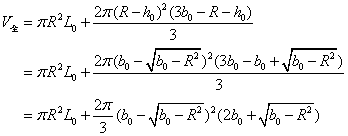
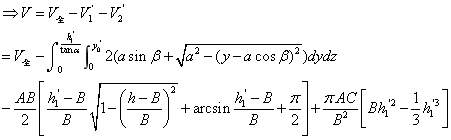
情形Ⅱ.当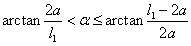 时, 时,
(1)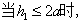 该情况的图示如下: 该情况的图示如下:
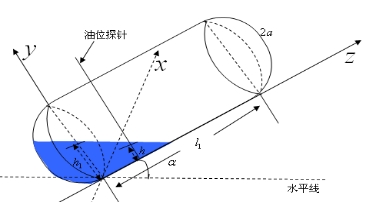
图4- 19
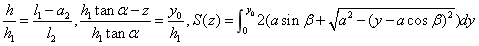


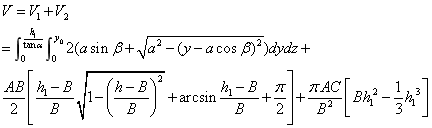
(2) 该情况如图4-20所示: 该情况如图4-20所示:
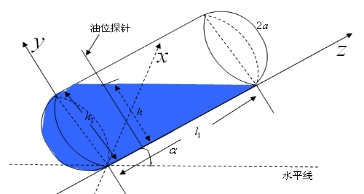
图4- 20
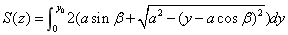
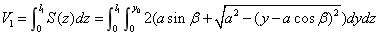
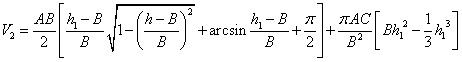
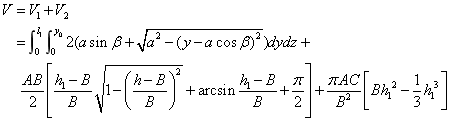
(3)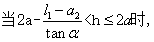 该情况如图4-21所示: 该情况如图4-21所示:
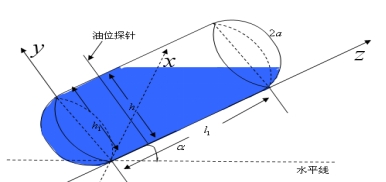
图4- 21
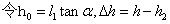
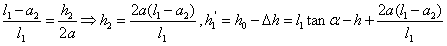
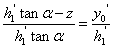 , ,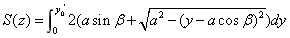
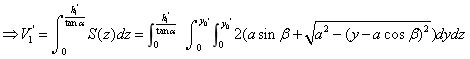
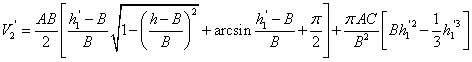
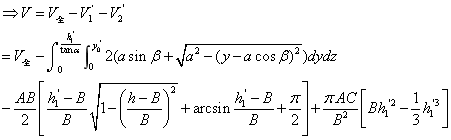
情形Ⅲ.当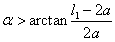 时, 时,
(1)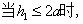 该情况如图4-22所示: 该情况如图4-22所示:
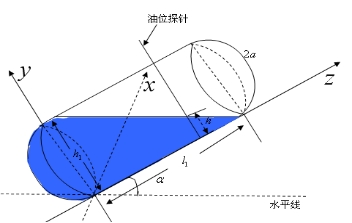
图4- 22
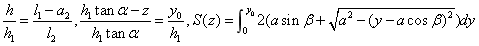
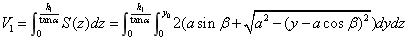
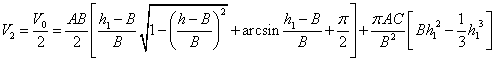
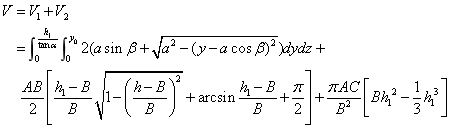
(2)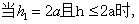 该情况如图4-23所示: 该情况如图4-23所示:
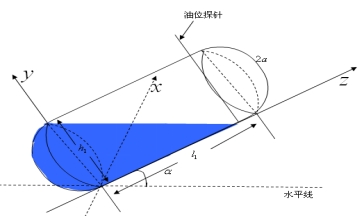
图4- 23
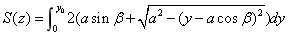
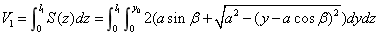
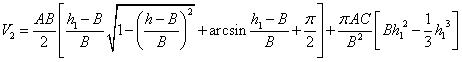

五 模型的评价和改进方向
1、模型的进一步讨论
就第二问我们在上述讨论一般情况分析的基础上对左半部分进行了详细的分析。
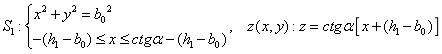

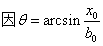
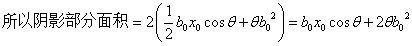
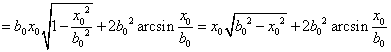


以下方程用来求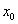 : :

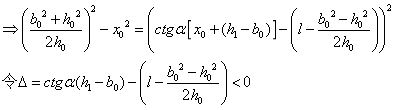
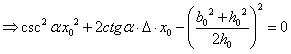
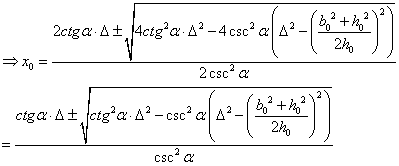

首先我们求出截面和球冠体的交线:
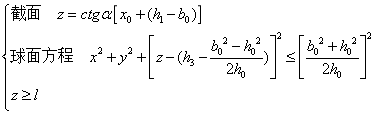
2、模型的优缺点
(1)对于问题一,从储油罐无变位与变位两个方面建立了模型,求得的储油量理论值与储油量实际值吻合得较好,相对误差小;特别是水平时相对误差稳定,符合要求,因此能准确的预测出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于问题二,先就一般情况考虑,再细分成8种情形,思维缜密,考虑周到。利用Matlab软件求出 值,求得各高度下的储油量理论值与储油量实际值吻合得较好,相对误差小,符合要求,因此能准确的预测出罐体变位后油位高度间隔为10cm的罐容表标定值。
(3)模型实用性好,具有很强的现实应用指导意义,数学推导严谨,理论性强。
(4)模型的假设不够充分,对误差的检验不够详细,没有从多方面进行误差诊断。
参考文献:
【1】韩中庚.数学建模竞赛-获奖论文精选与点评[M].北京:科学出
社,2007.
【2】王文波.数学建模及其基础知识详解[M].武汉:武汉大学出版社,2006.
【3】王庚,王敏生.现代数学建模方法[M].北京:科学出版社,2006.
【4】赵静,但琦.数学建模与数学实验[M].北京:高等教育出版社,2007.
【5】姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2003.
【6】冯杰,黄力伟,王勤,尹成义.数学建模原理与案例[M].北京:科学出版
社,2007.
附录
程序youliang1
load jinyou1.txt
load chuyou1.txt
g1=jinyou1(:,2)*10^(-2);
g2=chuyou1(:,2)*10^(-2);
syms a b h l
a=0.89*10;b=0.6*10;l=2.45*10;
V=(a*l/b).*((h-b).*((2.*h.*b-h.^2).^0.5)+b.^2.*asin((h-b)./b)+0.5.*b.^2*pi);
V1=subs(V,h,g1)
V2=subs(V,h,g2)
h1=jinyou1(:,1)+262;
h2=3706.91+262-chuyou1(:,1);
c1=V1-h1
c2=V2-h2
x1=abs(V1-h1)./V1
x2=abs(V2-h2)./V2
plot(g1,V1,'.r',g1,h1,'.c')
xlabel('进油后储油量');
ylabel('罐内油位高度');
title('罐内油位高度随进油后储油量的变化情况')
legend('储油理论量','储油实际量')
grid on
figure(2)
plot(g2,V2,'.r',g2,h2,'.c')
xlabel('出油后储油量');
ylabel('罐内油位高度');
title('罐内油位高度随出油后储油量的变化情况')
legend('储油理论量','储油实际量')
grid on
figure(3)
subplot(2,1,1)
plot(g1,c1,'.b')
xlabel('罐内油位高度');
ylabel('进油后储油量的误差');
title('进油后储油量的误差随罐内油位高度的变化情况')
grid on
subplot(2,1,2)
plot(g2,c2,'.b')
xlabel('罐内油位高度');
ylabel('出油后储油量的误差');
title('出油后储油量的误差随罐内油位高度的变化情况')
grid on
程序youliang2
load jinyou2.txt
load chuyou2.txt
g1=jinyou2(:,2)*10^(-2);
g2=chuyou2(:,2)*10^(-2);
syms a b h m a1
a=0.89*10;
b=0.6*10;
a1=0.4*10;
L=2.45*10;
m=4.1*pi/180;
k=(a1*tan(m)/b)-1;
p=(h+a1*tan(m)-b)/b;
q=(h+a1*tan(m)-b-L*tan(m))/b;
V=-((-1/3)*(1-q.^2).^(3/2)+(1-q.^2).^(1/2)+q.*asin(q)+1/3.*(1-p.^2).^(3/2)-(1-p.^2).^(1/2)-p.*asin(p)+pi*(q-p)*0.5).*a*b^2./tan(m)
V1=subs(V,h,g1)
V2=subs(V,h,g2)
h1=jinyou2(:,1)+215;
h2=3299.74+215-chuyou2(:,1);
c1=V1-h1
c2=V2-h2
x1=abs(V1-h1)./V1
x2=abs(V2-h2)./V2
plot(g1,V1,'.r',g1,h1,'.c')
xlabel('倾斜时进油后储油量');
ylabel('罐内油位高度');
title('倾斜时罐内油位高度随进油后储油量的变化情况')
legend('储油理论量','储油实际量')
grid on
figure(2)
plot(g2,V2,'.r',g2,h2,'.c')
xlabel('倾斜时出油后储油量');
ylabel('罐内油位高度');
title('倾斜时罐内油位高度随出油后储油量的变化情况')
legend('储油理论量','储油实际量')
grid on
figure(3)
subplot(2,1,1)
plot(g1,c1,'.b')
xlabel('罐内油位高度');
ylabel('倾斜时进油后储油量的误差');
title('倾斜时进油后储油量的误差随罐内油位高度的变化情况')
grid on
subplot(2,1,2)
plot(g2,c2,'.b')
xlabel('罐内油位高度');
ylabel('倾斜时出油后储油量的误差');
title('倾斜时出油后储油量的误差随罐内油位高度的变化情况')
grid on , 储油罐的变位识别与罐容表标定
摘要
本文通过对储油罐中油位高度及变位参数之间的不同情形的储油量进行分析并建立相应的数学模型,在该过程中先利用投影法、截面法及微元法得出储油量与油位高度及变位参数的函数关系。再由Matlab编程可知各高度储油量的理论数据,最后分析误差及评价模型的合理性。
对于问题一的任一种情形,我们均建立笛卡尔坐标系,当储油罐无变位时,利用微元法得到体积关于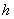 的公式,当储油罐发生变位时,根据储油罐中油量的多少分成三种情形,就每一类利用微元法得到体积关于 的公式,当储油罐发生变位时,根据储油罐中油量的多少分成三种情形,就每一类利用微元法得到体积关于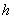 的公式。代人附件1实验数据中的高度得到储油罐中的理论油量 的公式。代人附件1实验数据中的高度得到储油罐中的理论油量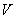 。根据理论油量及实际油量得出误差,判断误差所服从的分布,再利用相对误差进行误差分析并评价模型的合理性。由上述得到储油罐发生变位时体积关于 。根据理论油量及实际油量得出误差,判断误差所服从的分布,再利用相对误差进行误差分析并评价模型的合理性。由上述得到储油罐发生变位时体积关于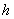 的公式我们给出了罐体变位后油位高度间隔为1cm的罐容表标定值(即进/出油量与罐内油位高度的表格)。 的公式我们给出了罐体变位后油位高度间隔为1cm的罐容表标定值(即进/出油量与罐内油位高度的表格)。
对于问题二中的储油罐,我们先将问题进行简化考虑,得出了储油罐水平卧放时油量与浮油子高度的函数关系;再考虑储油量与油位高度及变位参数(纵向倾斜角度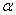 和横向偏转角度 和横向偏转角度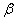 )的一般情况,在该过程中,我们进行近似处理,利用投影法和截面法得出了储油量关于油位高度及变位参数的函数关系;并在固定的横向偏转角度 )的一般情况,在该过程中,我们进行近似处理,利用投影法和截面法得出了储油量关于油位高度及变位参数的函数关系;并在固定的横向偏转角度 条件下,就纵向倾斜角度 条件下,就纵向倾斜角度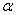 的变化进行分成三类讨论,这三类又可以分成八种情形,得到了每一种情形下实际储油罐罐内储油量与油位高度的函数关系。 的变化进行分成三类讨论,这三类又可以分成八种情形,得到了每一种情形下实际储油罐罐内储油量与油位高度的函数关系。
在模型的改进中,我们就问题二储油量与油位高度及变位参数的一般情况进行了仔细的考虑,将含油部分的体积分成四个部分,每一个部分将上述所提到的积分方法相结合,得到了各个部分的储油量与油位高度及变位参数的函数关系,从而可得总储油量与油位高度及变位参数的函数关系;并据此利用Matlab编程和实际测量的数据求得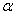 和 和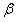 值;与此同时我们可以得出在固定 值;与此同时我们可以得出在固定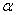 、 、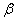 值时各高度下的理论储油量;根据理论油量及实际油量得出误差,判断误差所服从的分布再利用相对误差进行误差分析并评价模型的合理性。由上述得到储油罐发生变位时体积关于 值时各高度下的理论储油量;根据理论油量及实际油量得出误差,判断误差所服从的分布再利用相对误差进行误差分析并评价模型的合理性。由上述得到储油罐发生变位时体积关于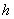 的公式我们给出了罐体变位后油位高度间隔为10cm的罐容表标定值。 的公式我们给出了罐体变位后油位高度间隔为10cm的罐容表标定值。
【关键词】投影法 截面法 微元法 Matlab编程
一、问题的提出
通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。按照有关规定,需要定期对罐容表进行重新标定。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为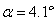 的纵向变位两种情况做了实验,实验数据如附件1所示。请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。 的纵向变位两种情况做了实验,实验数据如附件1所示。请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度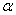 和横向偏转角度 和横向偏转角度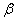 )之间的一般关系。请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。 )之间的一般关系。请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
二、问题的分析
1、对问题一的分析
当储油罐无变位时,储油罐圆柱体的接地一端为原点,以圆柱体高方向为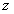 轴,建立笛卡尔坐标系,利用微元法得到体积关于 轴,建立笛卡尔坐标系,利用微元法得到体积关于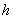 的公式,代人附件1实验数据中的高度得到储油罐中的理论油量 的公式,代人附件1实验数据中的高度得到储油罐中的理论油量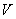 。利用附件1实验数据中得到储油罐中的实际油量,根据理论油量及实际油量就可以得出误差,判断误差所服从的分布,利用相对误差进行误差分析。 。利用附件1实验数据中得到储油罐中的实际油量,根据理论油量及实际油量就可以得出误差,判断误差所服从的分布,利用相对误差进行误差分析。
当储油罐发生变位时,以储油罐圆柱体的接地一端为原点,圆柱体高方向为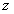 轴,建立笛卡尔坐标系。根据储油罐中油量的多少分成三类,然后就每一类利用微元法得到体积关于 轴,建立笛卡尔坐标系。根据储油罐中油量的多少分成三类,然后就每一类利用微元法得到体积关于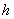 的公式,代人附件1实验数据中的高度得到储油罐中的理论油量 的公式,代人附件1实验数据中的高度得到储油罐中的理论油量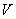 。利用附件1实验数据中得到储油罐中的实际油量,根据理论油量及实际油量就可以得出误差,判断误差所服从的分布,利用相对误差进行误差分析。 。利用附件1实验数据中得到储油罐中的实际油量,根据理论油量及实际油量就可以得出误差,判断误差所服从的分布,利用相对误差进行误差分析。
由上述得到储油罐发生变位时体积关于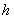 的公式可以给出罐体变位后油位高度间隔为1cm的罐容表标定值(即进/出油量与罐内油位高度的表格)。 的公式可以给出罐体变位后油位高度间隔为1cm的罐容表标定值(即进/出油量与罐内油位高度的表格)。
2、对问题二的分析
对于实际储油罐,我们首先将问题进行简化考虑,得出了当实际储油罐水平卧放时实际储油罐中油量与浮油子高度的函数关系;
然后我们先考虑实际储油罐罐内储油量与油位高度及变位参数(纵向倾斜角度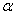 和横向偏转角度 和横向偏转角度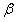 )的一般情况,在该过程中,我们进行近似处理,利用投影法和截面法得出了储油量关于油位高度及变位参数的函数关系,再在固定的横向偏转角度 )的一般情况,在该过程中,我们进行近似处理,利用投影法和截面法得出了储油量关于油位高度及变位参数的函数关系,再在固定的横向偏转角度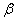 条件下,就纵向倾斜角度 条件下,就纵向倾斜角度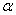 的变化进行分类讨论,一共有三种情形,得到了每一种情形下实际储油罐罐内储油量与油位高度的函数关系。 的变化进行分类讨论,一共有三种情形,得到了每一种情形下实际储油罐罐内储油量与油位高度的函数关系。
最后我们先利用附件2中的少量实际数据得出了附件2所处状态下的纵向倾斜角度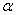 和横向偏转角度 和横向偏转角度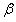 ,再利用附件2中给定各高度进行代人,得到实际储油罐理论的储油量,与实际储油量进行比较,求出误差及相对误差。 ,再利用附件2中给定各高度进行代人,得到实际储油罐理论的储油量,与实际储油量进行比较,求出误差及相对误差。
由上述得到储油罐发生变位时体积关于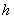 的公式可以给出罐体变位后油位高度间隔为10cm的罐容表标定值(即进/出油量与罐内油位高度的表格)。 的公式可以给出罐体变位后油位高度间隔为10cm的罐容表标定值(即进/出油量与罐内油位高度的表格)。
三 模型的假设和符号说明
1、模型假设
(1)在储油罐倾斜的情况下,忽略油浮子高度为0时油所占的体积;
(2)在储油罐倾斜的情况下,假设当油浮子高度达到最大后不再进油;
(3)油的挥发速度很慢,忽略因油的挥发而造成储油量的减少;
(4)储油罐的材料为钢体,忽略因渗出油而造成储油量的减少;
(5)储油罐管理妥当,不会因特殊情况而造成储油量的变化。
2、符号说明

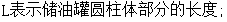
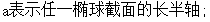
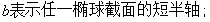
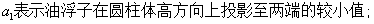
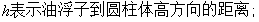
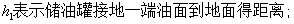
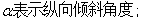
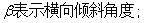
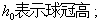

四 模型的建立与求解
问题一
当储油罐体无变位时,储油罐圆柱体的接地一端为原点,以圆柱体高方向为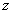 轴,建立笛卡尔坐标系,如图4-1所示,在高度为 轴,建立笛卡尔坐标系,如图4-1所示,在高度为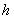 时,利用微元法过垂直 时,利用微元法过垂直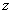 轴的方向做截面 轴的方向做截面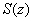 ,对 ,对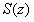 关于 关于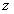 进行积分,得到体积关于 进行积分,得到体积关于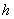 的公式。 的公式。
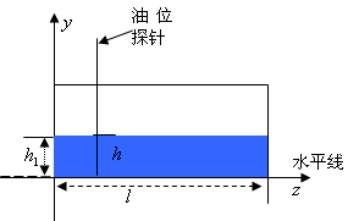
图4- 1
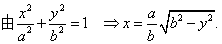
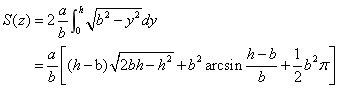
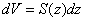
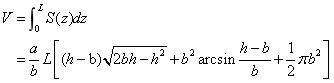 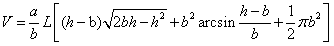
利用Matlab中的命令subs代人附件1实验数据中的各高度得到储油罐中的理论油量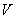 。 。
由附件1实验数据中进油量、出油量及储油罐罐内油量初值可以得到储油罐中的实际储油量,根据理论油量及实际油量就可以得出误差。
由附录中的程序youliang1,我们得到了理论储油量,误差及相对误差。
进油后理论储油量与实际储油量随高度的变化规律如图4-2所示:

图4- 2
出油后理论储油量与实际储油量随高度的变化规律如图4-3所示:
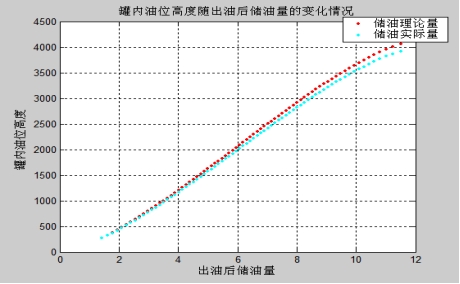
图4- 3
无变位进油和无变位出油的储油理论量和储油实际量及误差和相对误差的数据如表4-1所示:
表4- 1
|
无变位进油
|
无变位出油
|
|
储油量实际值
|
储油量理论值
|
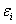 (误差) (误差)
|
相对误差
|
储油量实际值
|
储油量理论值
|
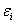 (误差) (误差)
|
相对误差
|
|
312
|
322.9
|
10.88
|
3.37%
|
3916.2
|
4052.8
|
136.61
|
3.37%
|
|
362
|
374.6
|
12.63
|
3.37%
|
3866.2
|
4001.0
|
134.86
|
3.37%
|
|
412
|
426.4
|
14.36
|
3.37%
|
3816.2
|
3949.3
|
133.13
|
3.37%
|
|
462
|
478.1
|
16.13
|
3.37%
|
3766.2
|
3897.6
|
131.38
|
3.37%
|
|
512
|
529.9
|
17.85
|
3.37%
|
3716.2
|
3845.8
|
129.65
|
3.37%
|
|
562
|
581.6
|
19.61
|
3.37%
|
3666.2
|
3794.1
|
127.88
|
3.37%
|
|
612
|
633.4
|
21.35
|
3.37%
|
3616.2
|
3742.3
|
126.16
|
3.37%
|
|
662
|
685.1
|
23.08
|
3.37%
|
3566.2
|
3690.6
|
124.39
|
3.37%
|
|
712
|
736.8
|
24.85
|
3.37%
|
3516.2
|
3638.8
|
122.65
|
3.37%
|
|
762
|
788.6
|
26.58
|
3.37%
|
3466.2
|
3587.1
|
120.92
|
3.37%
|
|
812
|
840.3
|
28.33
|
3.37%
|
3416.2
|
3535.4
|
119.17
|
3.37%
|
|
862
|
892.1
|
30.06
|
3.37%
|
3366.2
|
3483.6
|
117.43
|
3.37%
|
|
912
|
943.8
|
31.80
|
3.37%
|
3316.2
|
3431.9
|
115.70
|
3.37%
|
|
962
|
995.5
|
33.54
|
3.37%
|
3266.2
|
3380.1
|
113.94
|
3.37%
|
|
1012
|
1047.3
|
35.30
|
3.37%
|
3216.2
|
3328.4
|
112.18
|
3.37%
|
|
1062
|
1099.1
|
37.05
|
3.37%
|
3166.2
|
3276.6
|
110.45
|
3.37%
|
|
1112
|
1150.8
|
38.81
|
3.37%
|
3116.2
|
3224.9
|
108.70
|
3.37%
|
|
1162
|
1202.6
|
40.55
|
3.37%
|
3066.2
|
3173.2
|
106.96
|
3.37%
|
|
1212
|
1254.3
|
42.29
|
3.37%
|
3016.2
|
3121.4
|
105.22
|
3.37%
|
|
1262
|
1306.0
|
44.03
|
3.37%
|
2966.2
|
3069.7
|
103.46
|
3.37%
|
|
1312
|
1357.8
|
45.77
|
3.37%
|
2916.2
|
3017.9
|
101.73
|
3.37%
|
|
1362
|
1409.5
|
全套毕业设计论文现成成品资料请咨询微信号:biyezuopinvvp QQ:1015083682
返回首页
如转载请注明来源于www.biyezuopin.vip
|
|
|



