题 目 特殊工件磨削加工问题研究

摘 要
本文对特殊工件的磨削加工过程进行抽象、建模和求解;根据工件母线方程设计加工方案,并对方案进行了误差分析,然后提出修整策略。
磨床是通过下台、中台的平移变换和上台的旋转变换,使得工件母线始终与砂轮相切。为了便于坐标变换和建模,建立两个平面直角坐标系:底座和砂轮所在的刚性坐标系{A}和工件母线所在坐标系{B},其中,母线方程通过横轴正方向平移 b 变换到坐标系{B}。在{A}下设定加工基准,加工基准由砂轮的初始位置和上台的初始旋转角构成。根据工件母线方程设定砂轮几何尺寸,同时发现圆柱形砂轮是轮式砂轮圆弧半径趋近无穷时的特殊情况。
建立三层优化模型:第一层保证误差最小化(误差分析包括局部误差和全局误差, 局部误差是运动轨迹与母线方程在坐标系{B}下 y 方向偏差的最大值,全局误差是偏差的均值),通过优化工件在坐标系{B}下的磨削步长,得出指令的脉冲序列;第二层以磨削用时最小化为目标,优化脉冲指令的发射时间;第三层以脉冲频率变化最小为目标, 用三次样条插值优化脉冲分布,以使工作台稳定运行和加工表面光滑。
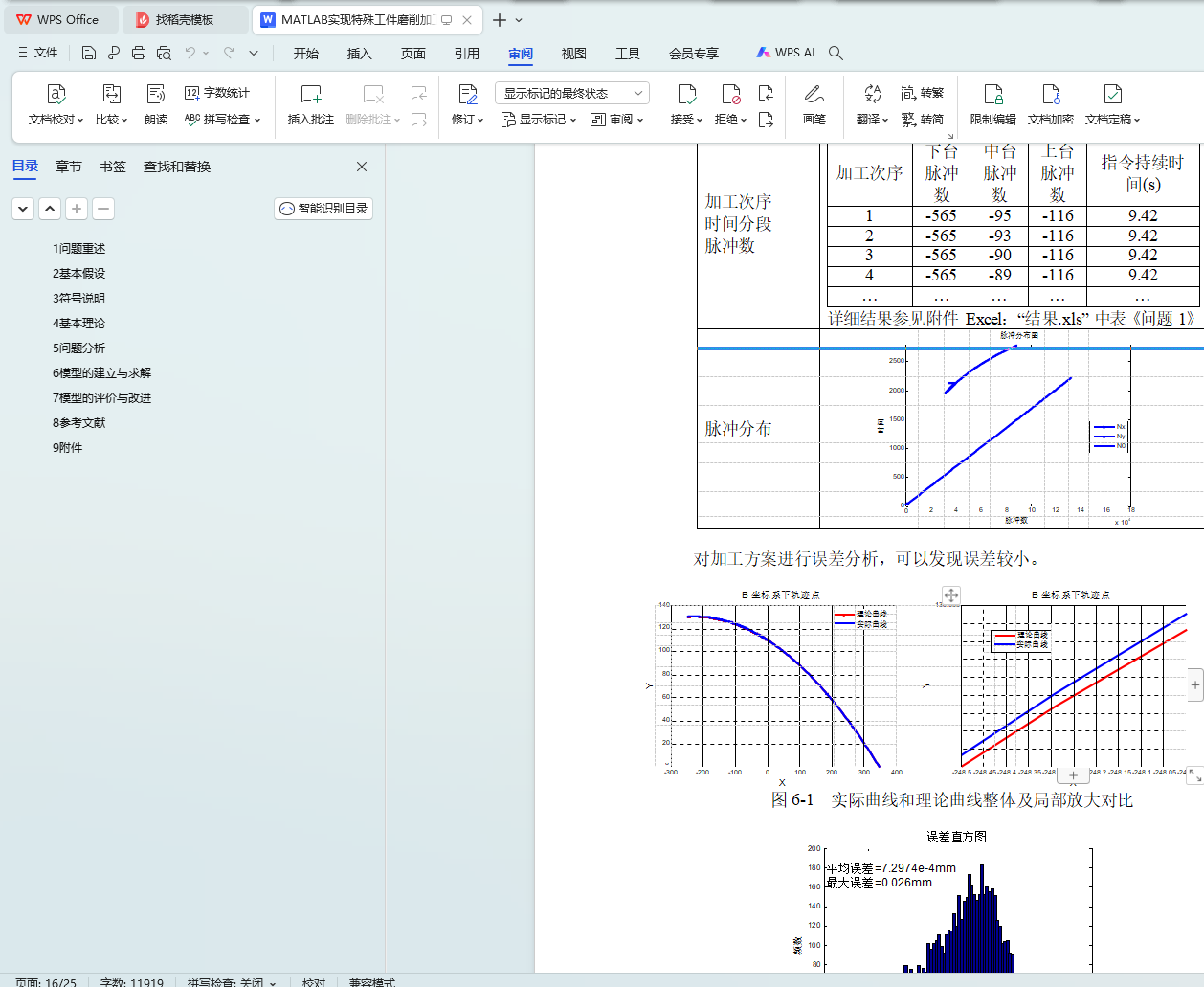
问题 1 和问题 2 中,认为切点位于垂直于砂轮转轴的中截面上,在坐标系{A}下是固定点,并在建模过程中要求工件母线始终在该点与砂轮接触并相切。根据母线方程, 利用坐标变换,误差分析策略等建立优化模型,确定加工基准、砂轮尺寸、脉冲数及分布,得出问题 1 和问题 2 中工件加工时耗分别为 46.75min 和 50.95min。
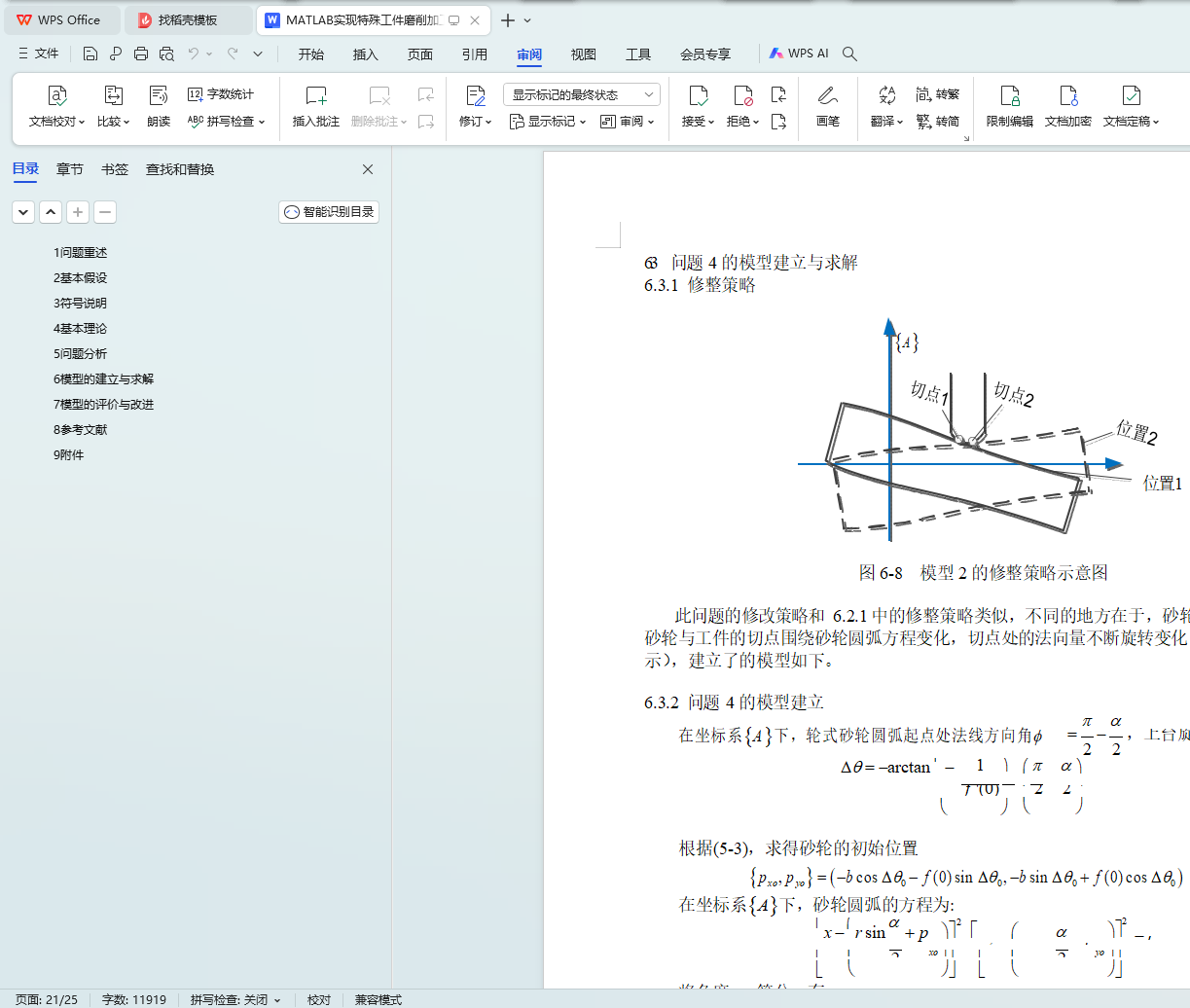
问题 3 和问题 4 实际上分别是对问题 1 和问题 2 策略的修整。这两个问题中的切点不断变化,以使得砂轮圆弧表面均匀磨损。问题 3 中的切点在坐标系{A}下沿 x 正向平移;问题 4 中的切点在坐标系{A}下沿砂轮圆弧旋转。模型思想分别类同问题 1 和问题
2,得到问题 3 和问题 4 中工件加工时耗分别为 45.19min 和 48.08min。文章最后对模型进行了评价,并针对不足的地方提出改进策略。
 关键词:特殊工件磨削 加工基准 坐标变换 脉冲指令工序 三层优化
关键词:特殊工件磨削 加工基准 坐标变换 脉冲指令工序 三层优化
目 录
1 问题重述 2
2 基本假设 2
3 符号说明 2
4 基本理论 3
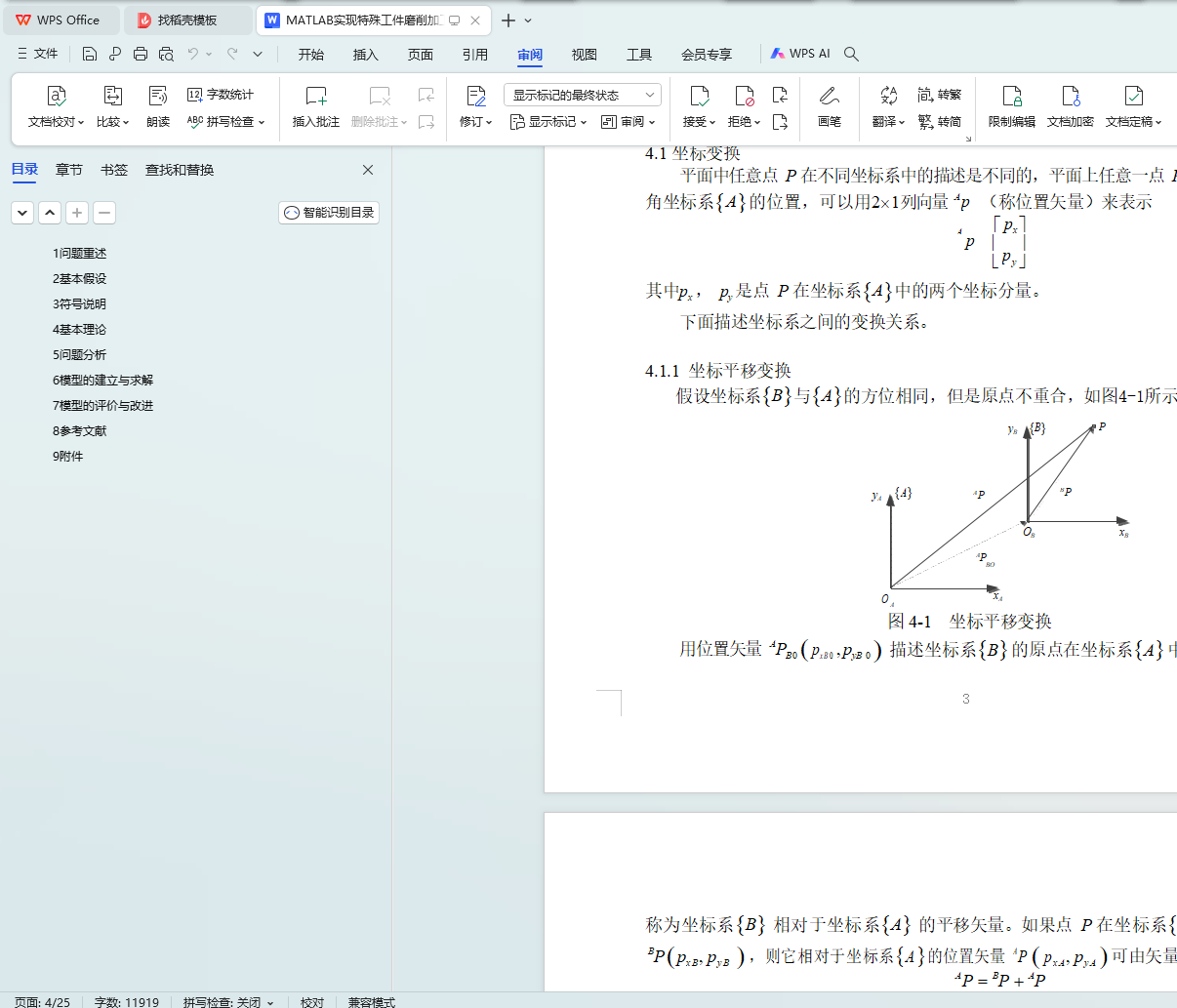
4.1 坐标变换 3
4.1.1 坐标平移变换 3
4.1.2 坐标旋转变换 4
4.1.3 一般变换 4
4.2 曲率的概念及计算 5
4.2.1 曲率的概念 5
4.2.2 曲率的计算公式 6
5 问题分析 6
5.1 设定坐标系 6
5.2 加工基准分析 7
5.3 砂轮尺寸几何分析 8
5.4 机理分析 9
5.5 误差原理 10
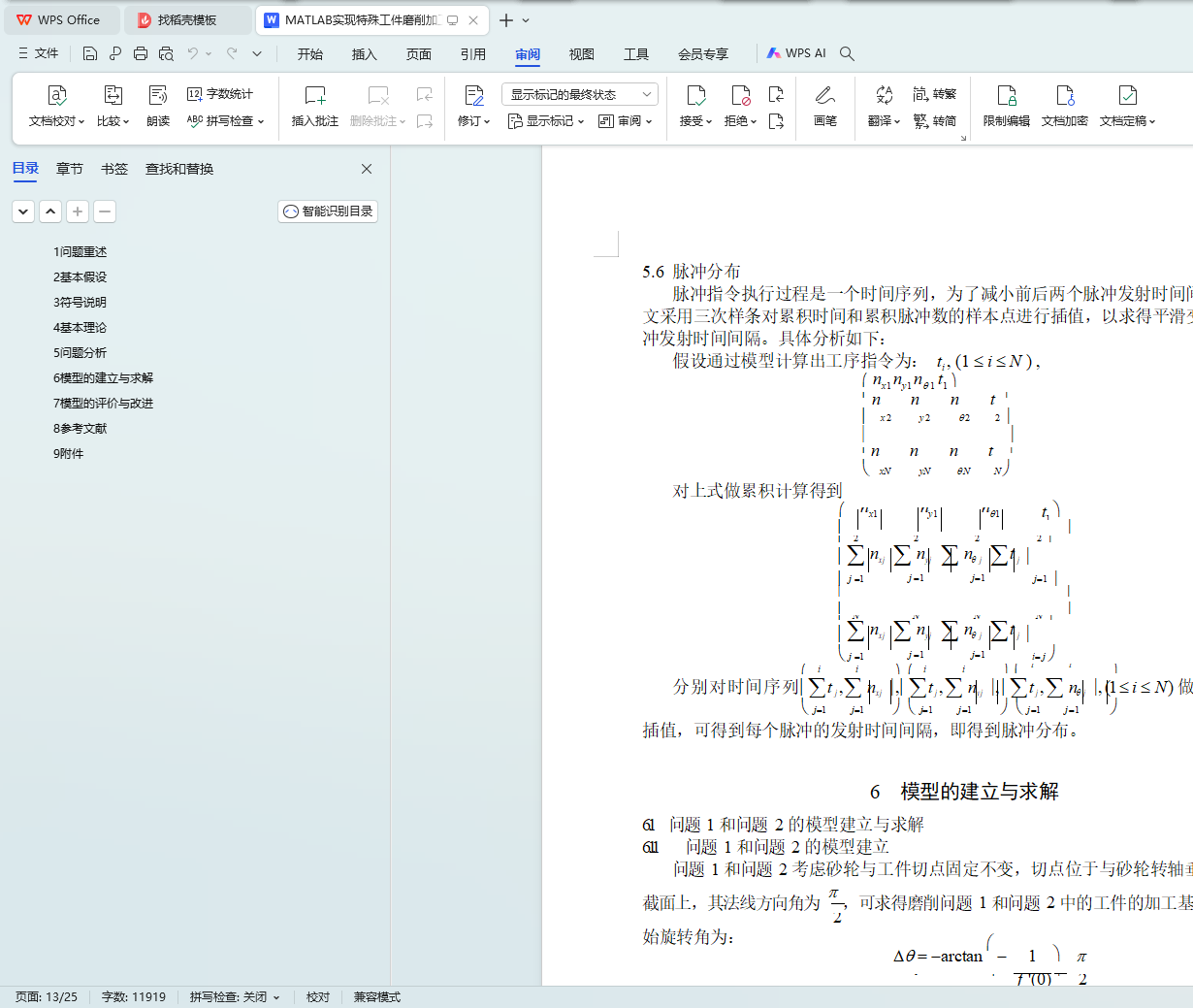
5.6 脉冲分布 11
6 模型的建立与求解 11
6.1 问题 1 和问题 2 的模型建立与求解 11
6.1.1 问题 1 和问题 2 的模型建立 11
6.1.2 问题 1 和问题 2 的模型求解 13
6.2 问题 3 的模型建立与求解 16
6.2.1 修整策略 16
6.2.2 问题 3 的模型建立 16
6.2.3 问题 3 的模型求解 17
6.3 问题 4 的模型建立与求解 19
6.3.1 修整策略 19
6.3.2 问题 4 的模型建立 19
6.3.3 问题 4 的模型求解 20
7 模型的评价与改进 21
7.1 模型的评价 21
7.2 模型的改进 22
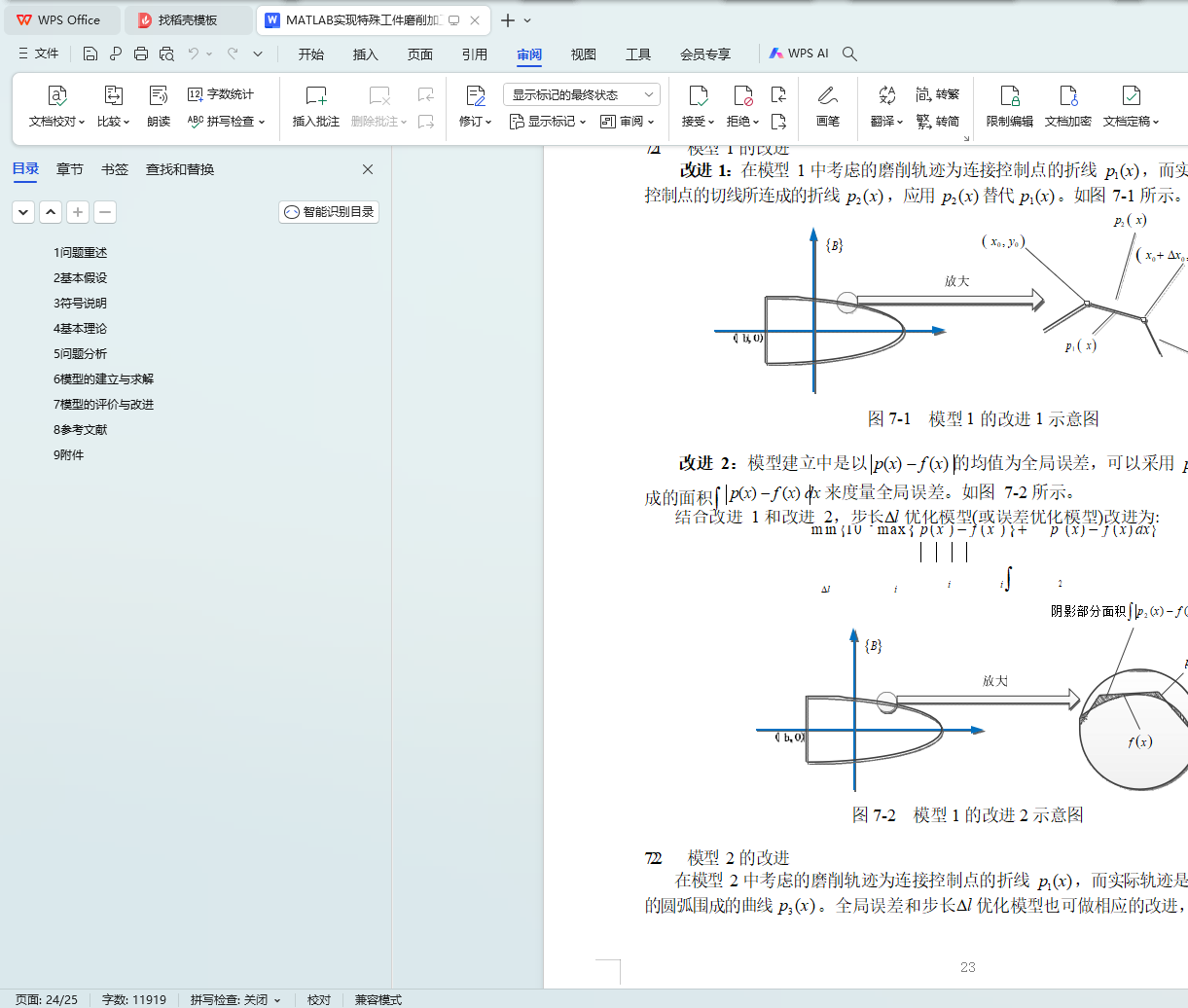
7.2.1 模型 1 的改进 22
7.2.2 模型 2 的改进 22
7.2.3 模型 3 的改进 23
7.2.4 模型 4 的改进 23
8 参考文献 23
9 附件 23