题 目 特殊工件磨削加工的数学模型研究

摘 要
本文主要以规划砂轮中心相对运动轨迹和砂轮作为研究对象,根据工件加工要求,运用工件包络加工方法和刀具插补运算方法建立了以加工时间最短,加工误差最小等目标的数学模型,给出了不同目标和约束下的加工方案,本文主要完成的工作有:
Ⅰ 分析了磨床的工作原理和工件加工方案的制定原则给出了加工方案的确定方法和误差的分析方法,在此基础上建立了数学模型。
Ⅱ 对问题Ⅰ,在满足加工要求的前提下,以加工误差最小和加工时间最短为目标函数,采用了包络加工方法和改进的机床插补算法,来制定加工方案,使用目标搜索方法得到了最优的加工方案,并求得次加工方案的加工误差。
Ⅲ 对问题Ⅱ,在满足加工要求的前提下,以加工误差最小和加工时间最短为目标函数,采用了包络加工方法和改进的机床插补算法,以轮式砂轮中的相对工件运动轨迹为研究对象,让中、下两台动而上台不动,砂轮的外端轮廓参数 r 小于母线的最小曲率半径,砂轮的侧面始终与加工母线垂直,并按照上述原则来制定加工方案,使用目标搜索法得到了最优的加工方案,并求得此方案的加工误差。
IV 通过改变加工步中 x、y 的增量而使加工过程中圆柱型砂轮表面的磨损均
匀
V 通过改变加工步中转角增量而使加工过程中砂轮表面磨损均匀
关键词:插补,包络,多项式插值,多级优化,磨损均匀
目录
题 目 特殊工件磨削加工的数学模型研究
摘 要
匀
一、 问题的重述和分析
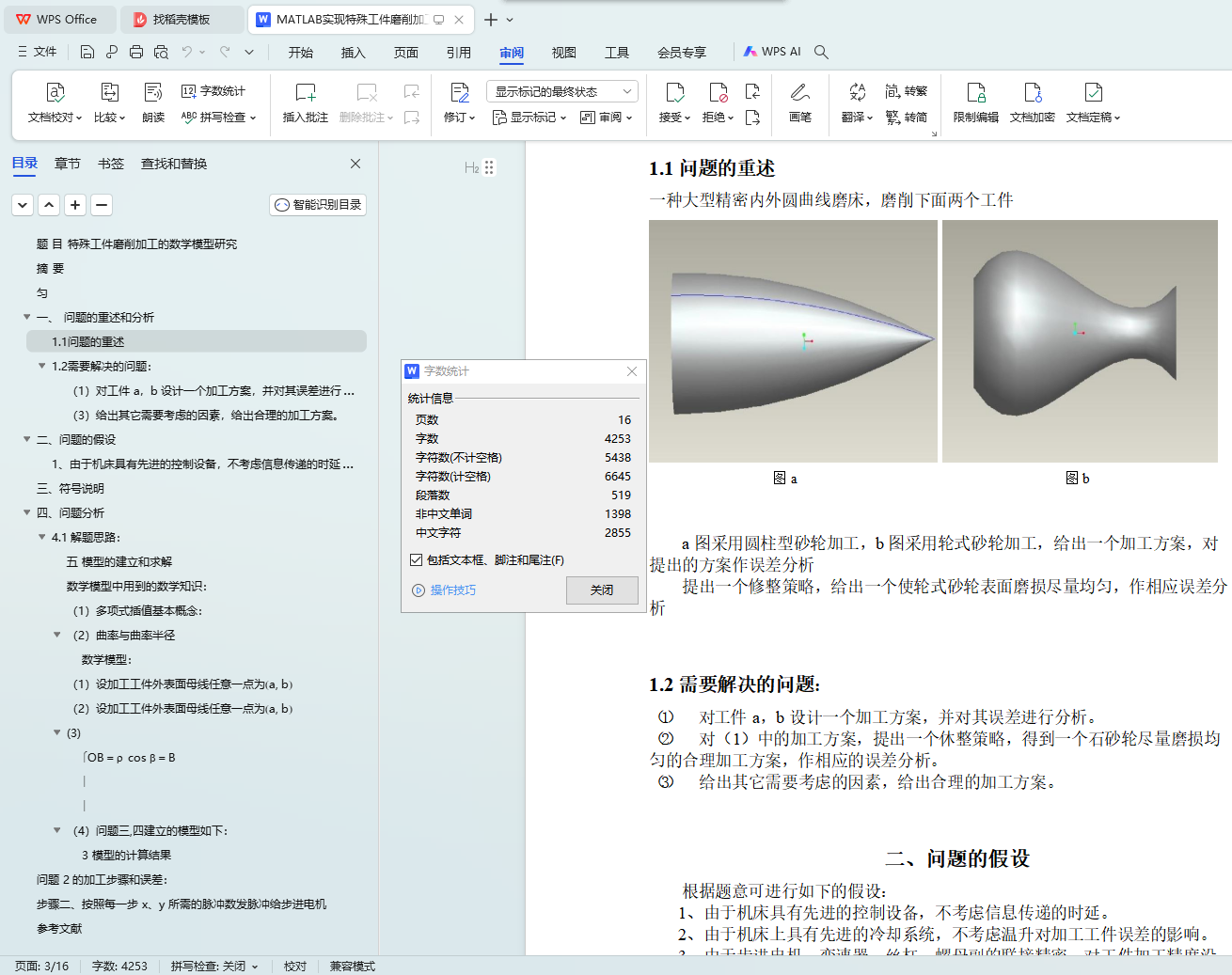
1.1 问题的重述
1.2 需要解决的问题:
(1) 对工件 a,b 设计一个加工方案,并对其误差进行分析。
(3) 给出其它需要考虑的因素,给出合理的加工方案。
二、问题的假设
1、由于机床具有先进的控制设备,不考虑信息传递的时延。
三、符号说明
四、问题分析
4.1 解题思路:
五 模型的建立和求解
数学模型中用到的数学知识:
(1)多项式插值基本概念:
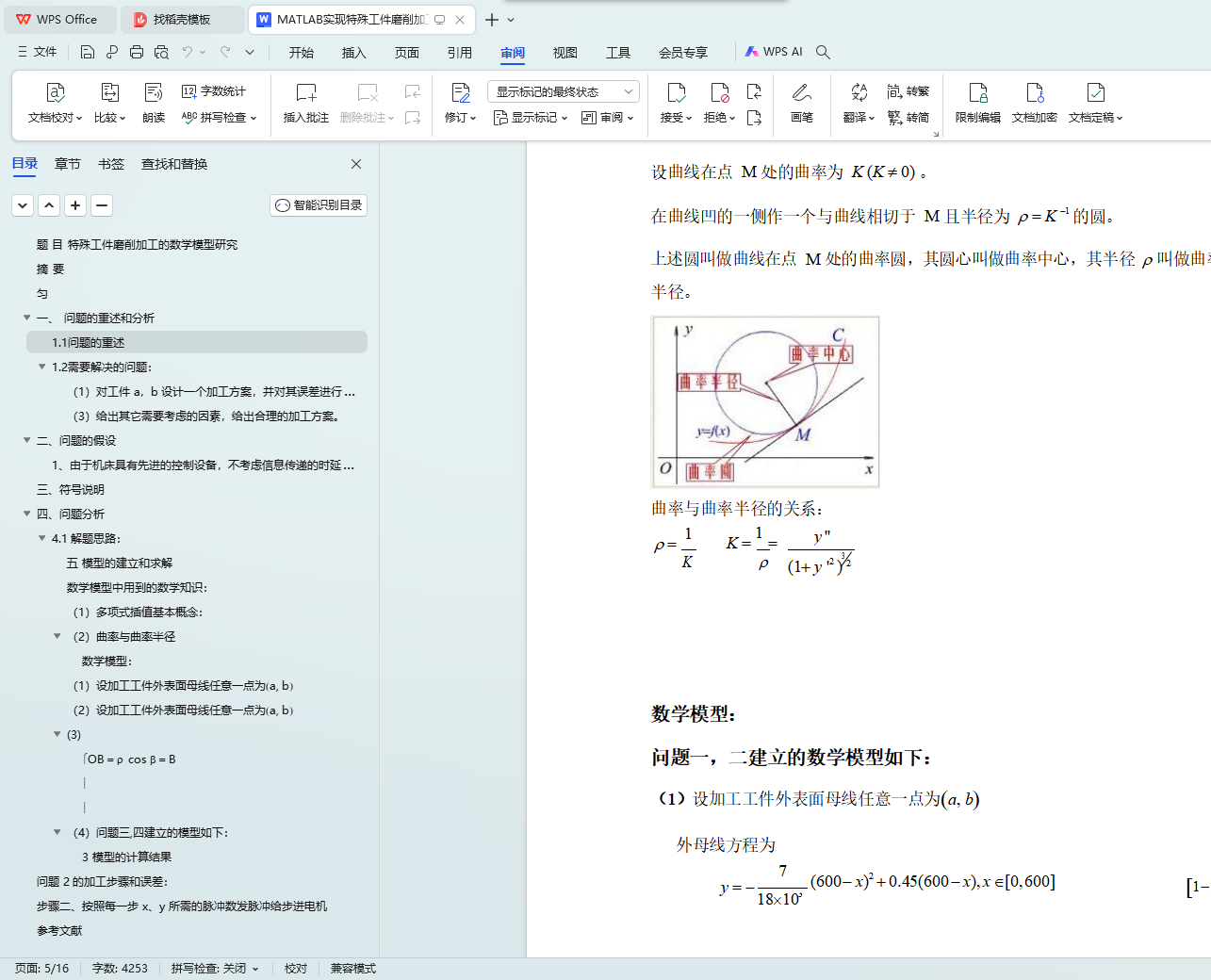
(2)曲率与曲率半径
数学模型:
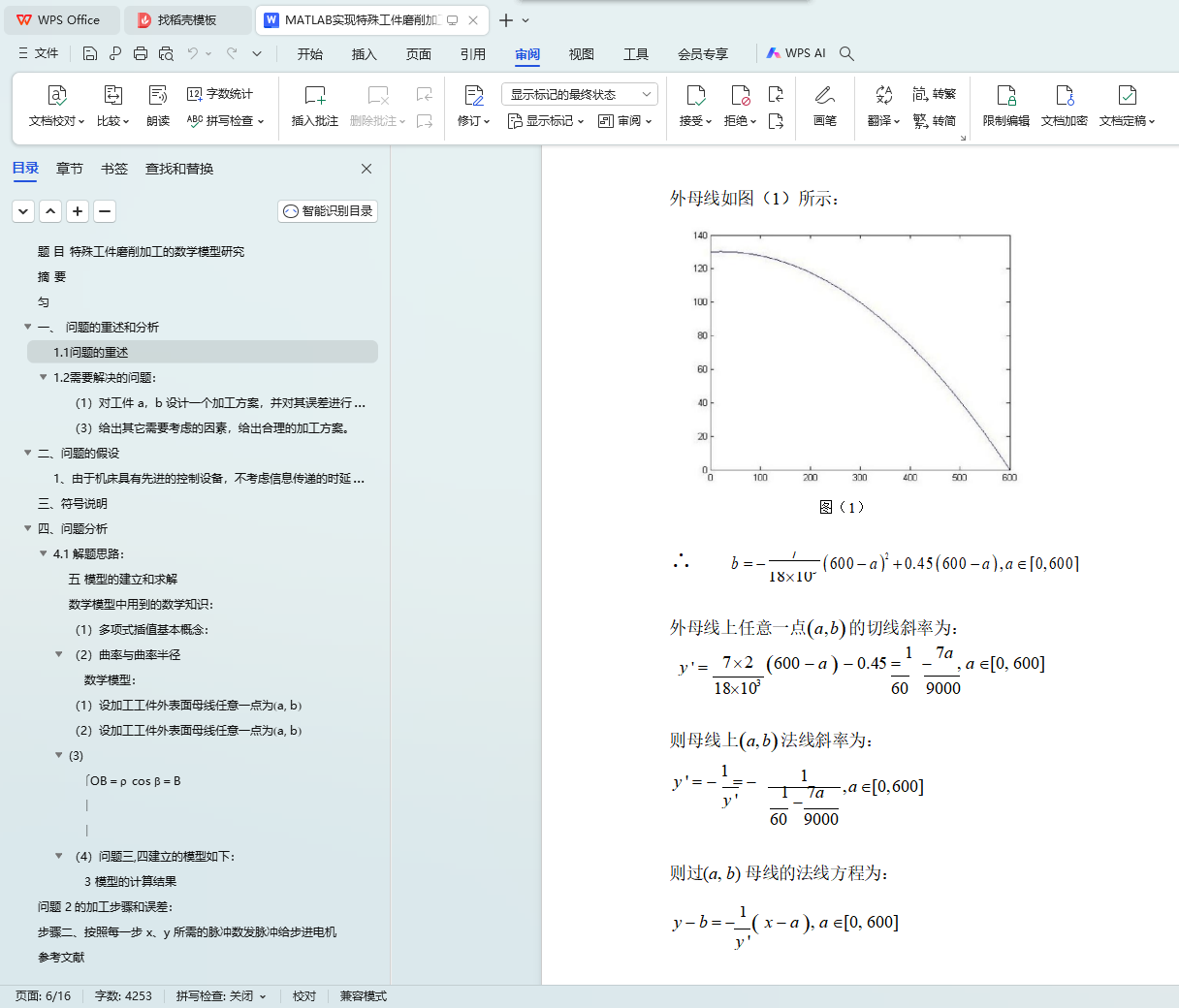
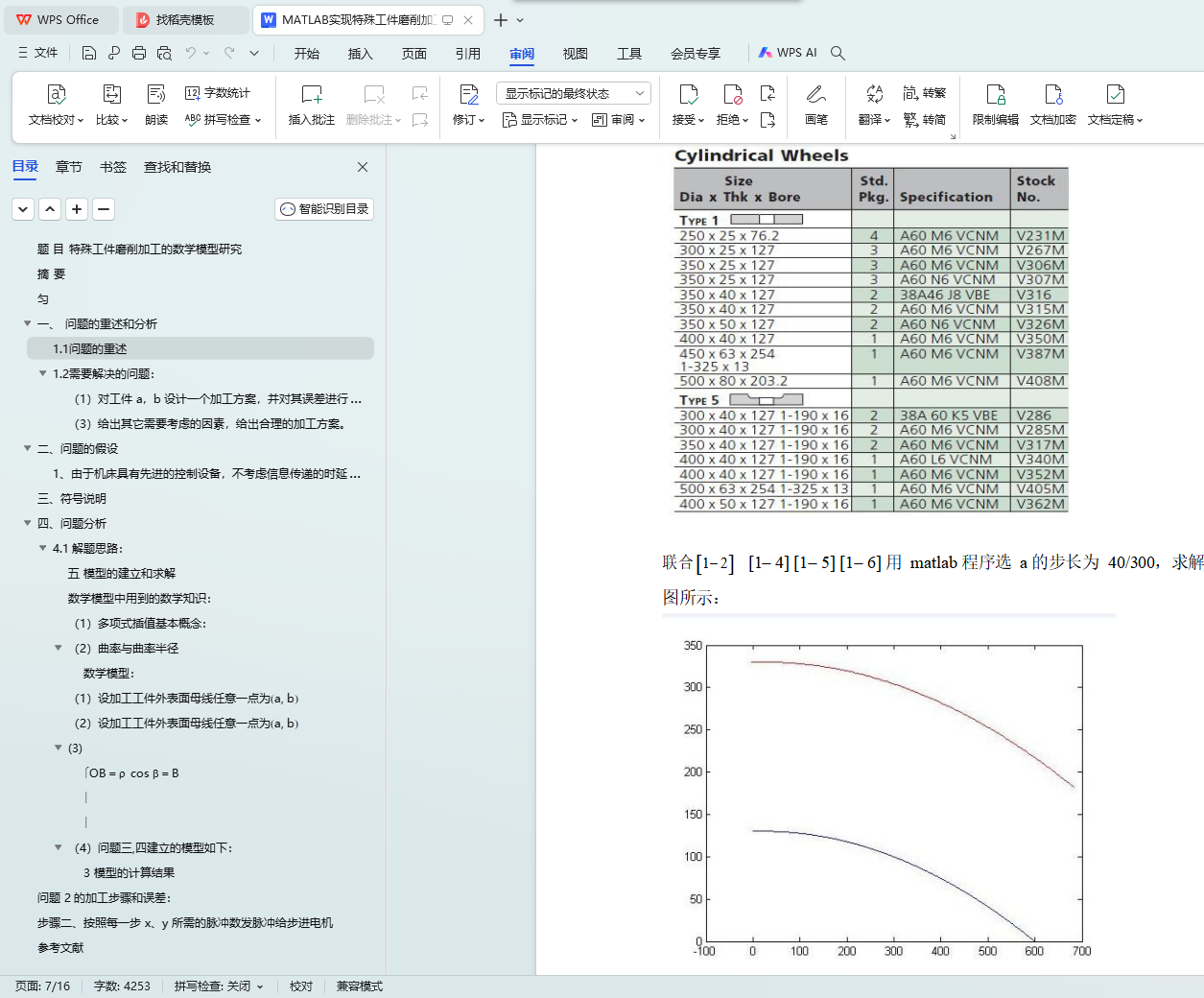
(1)设加工工件外表面母线任意一点为(a, b)
(2)设加工工件外表面母线任意一点为(a, b)
(3)
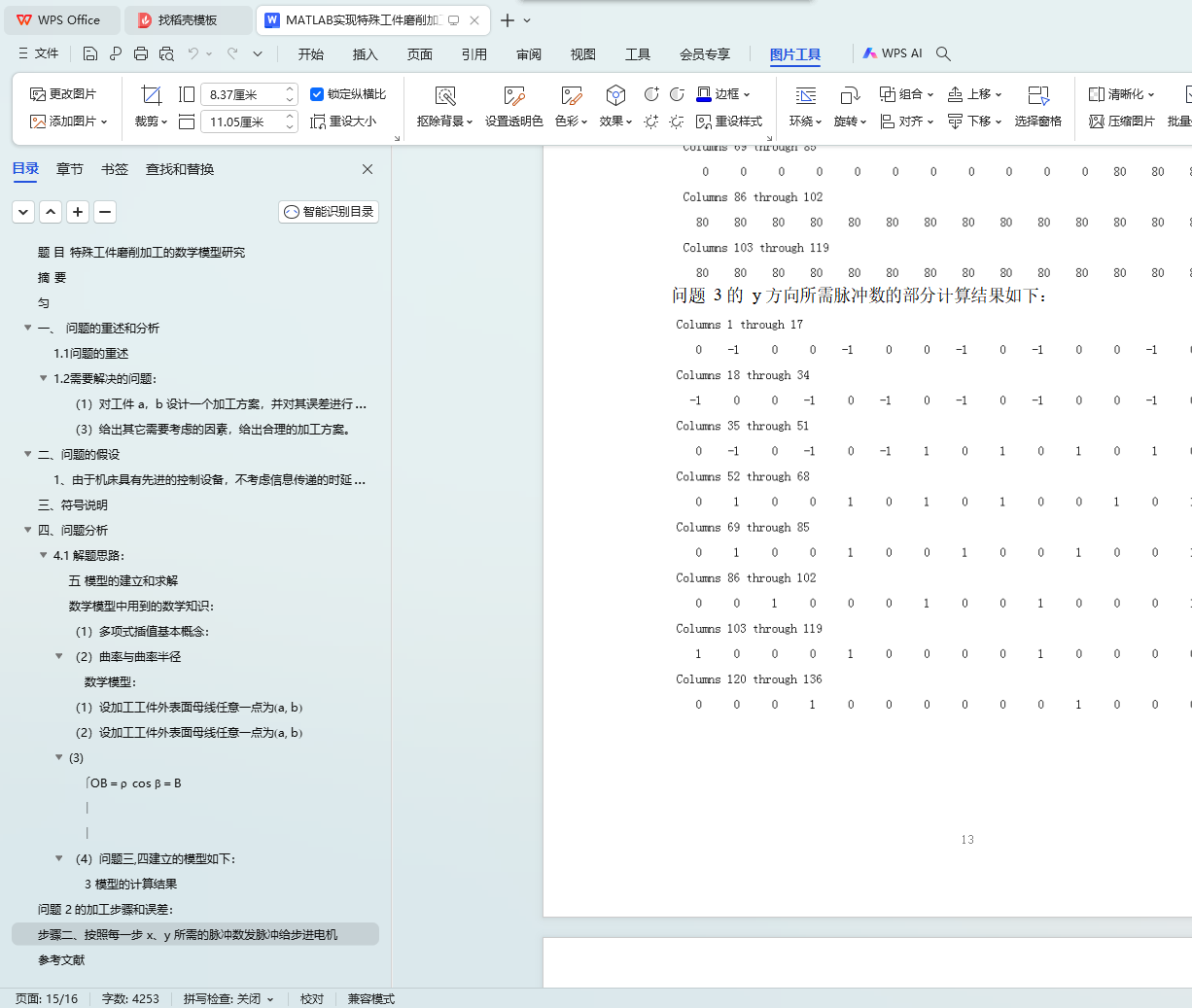
(4) 问题三,四建立的模型如下:
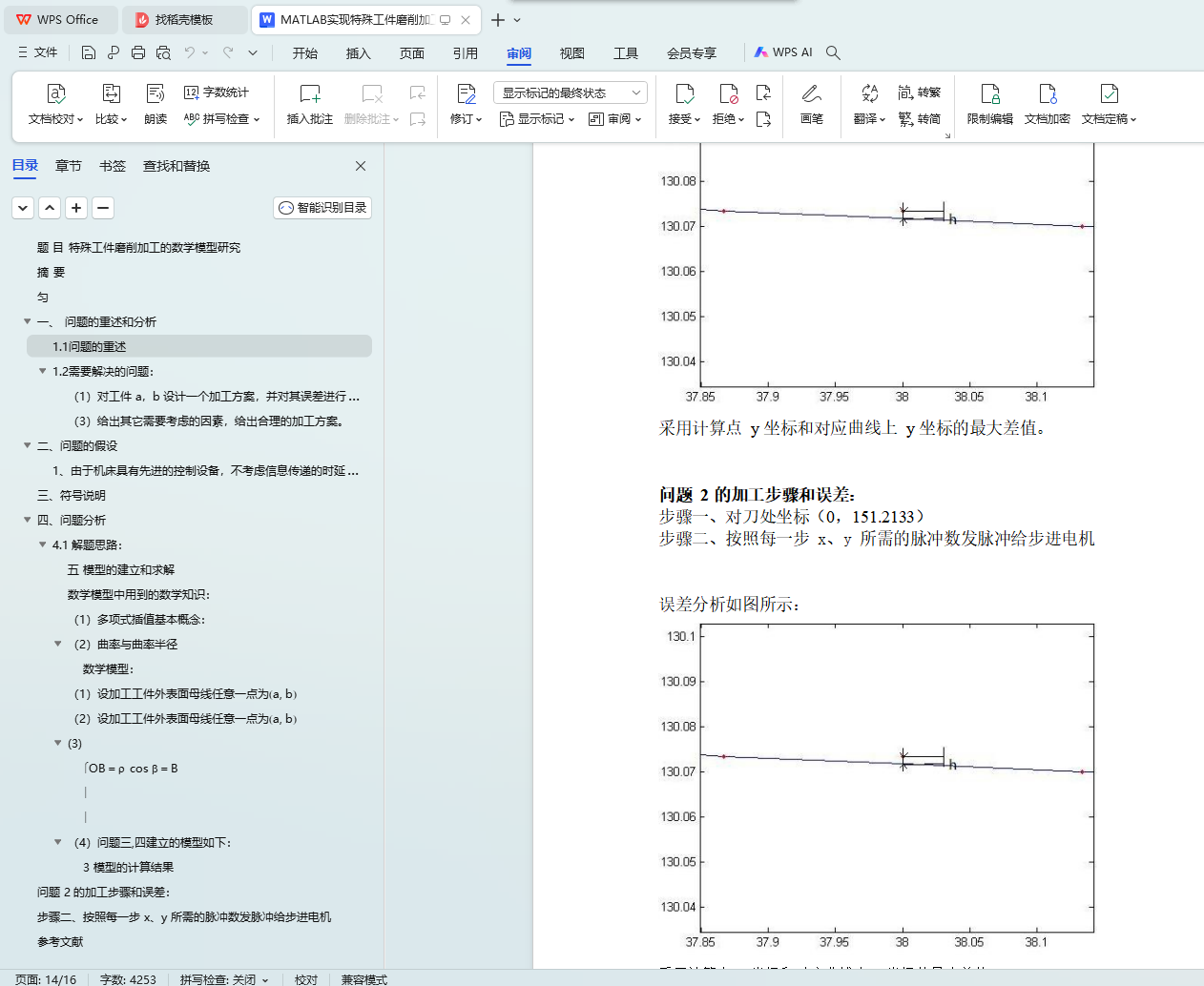
问题 2 的加工步骤和误差:
步骤二、按照每一步 x、y 所需的脉冲数发脉冲给步进电机
参考文献