题 目 基于卫星无源探测的空间飞行器主动段轨道估计与误差分析
题 目 基于卫星无源探测的空间飞行器主动段轨道估计与误差分析
摘 要:
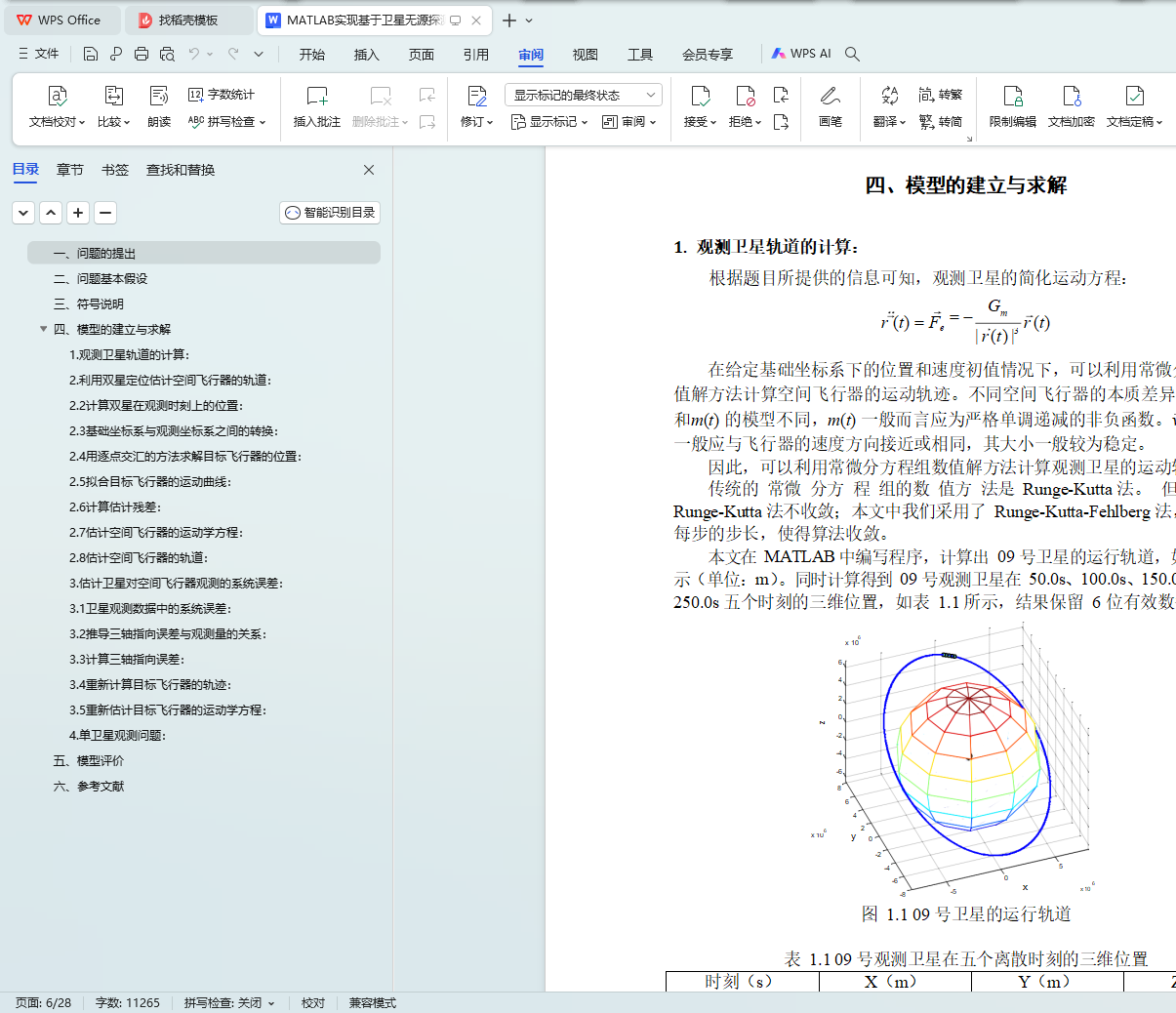
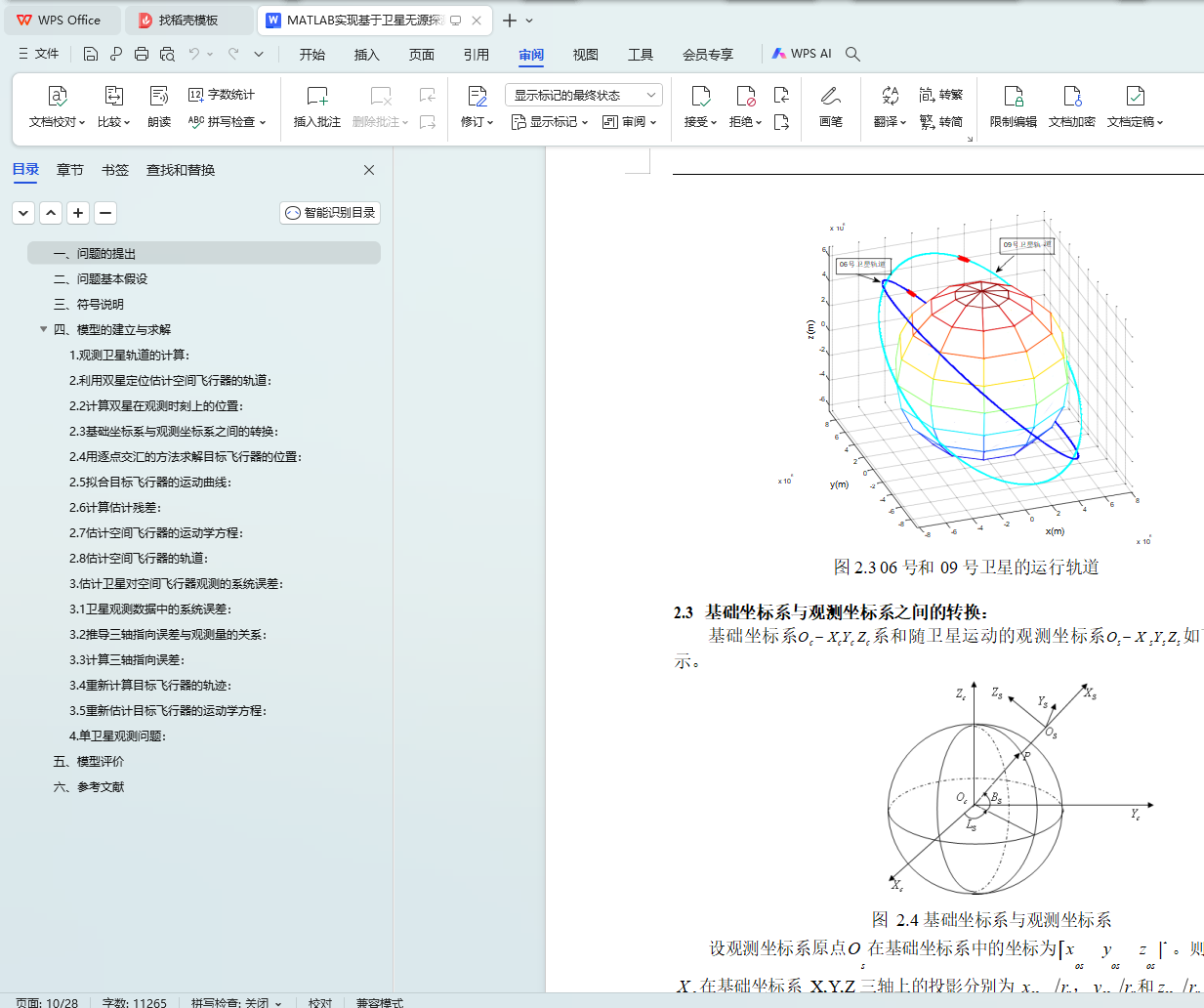
本文首先根据观测卫星的初始位置、速度,以及观测卫星的运动方程计算出卫星的轨道,并得到 09 号观测卫星在 50.0s、100.0s、150.0s、200.0s、250.0s 五个时刻的三维位置。
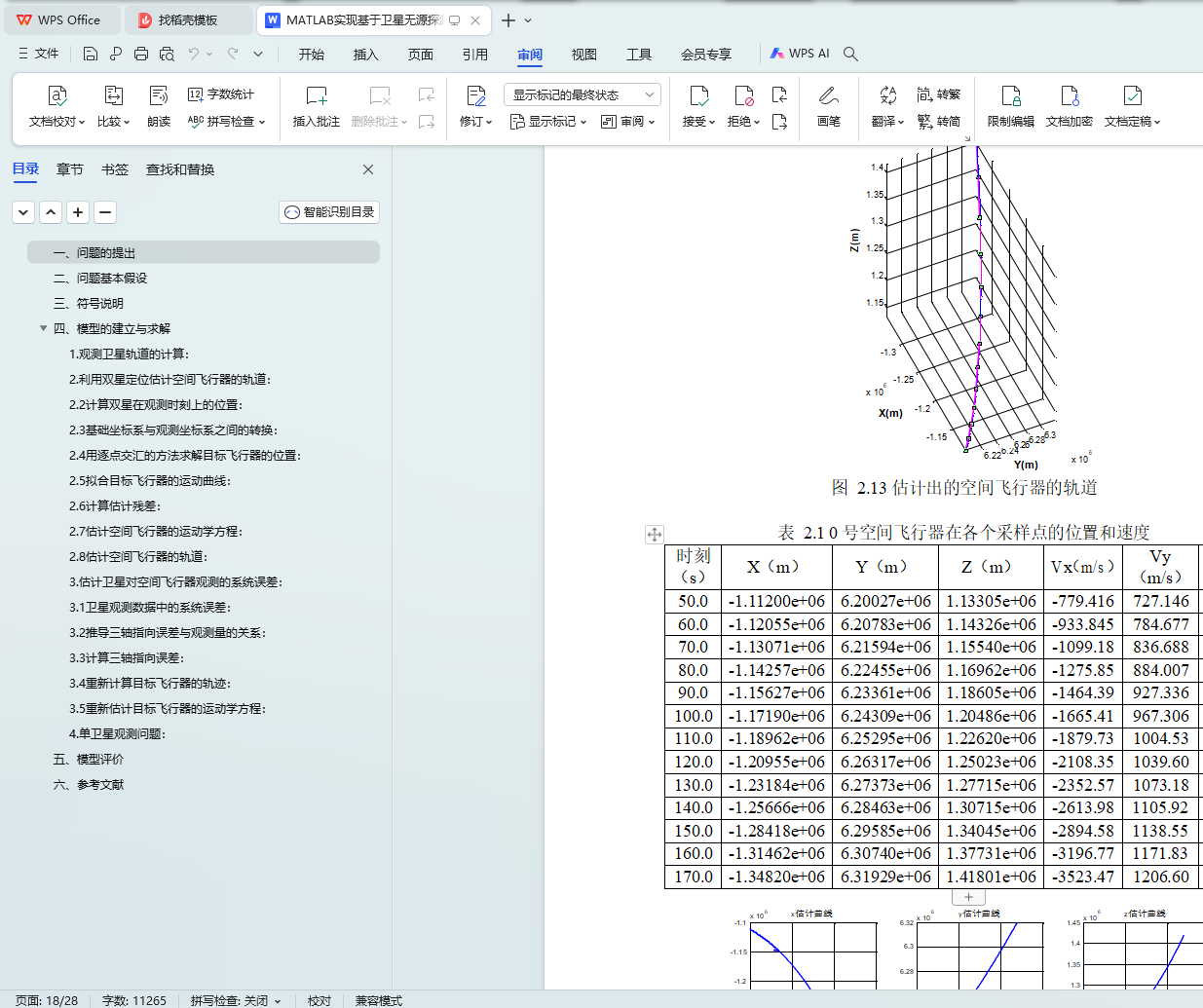
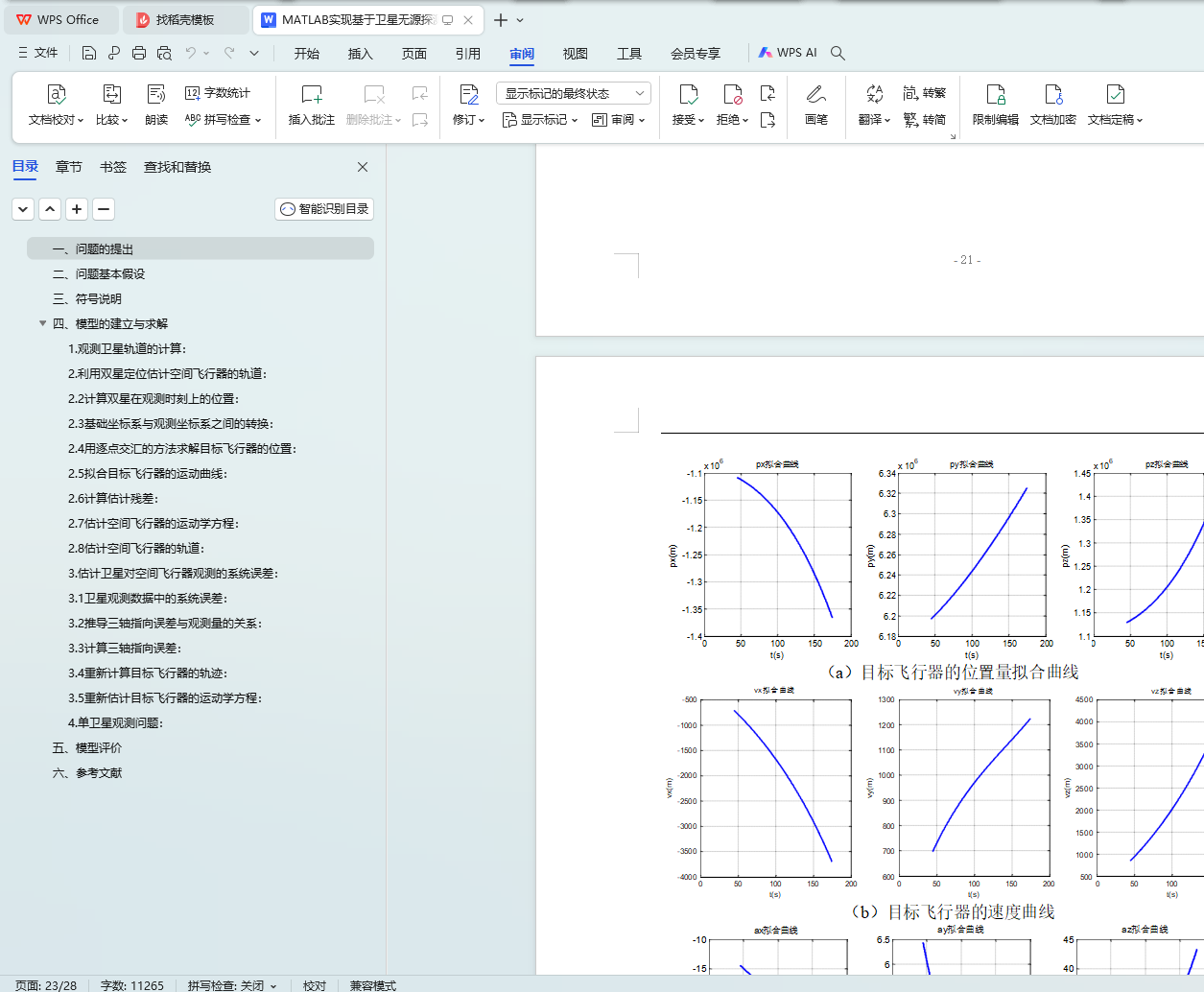
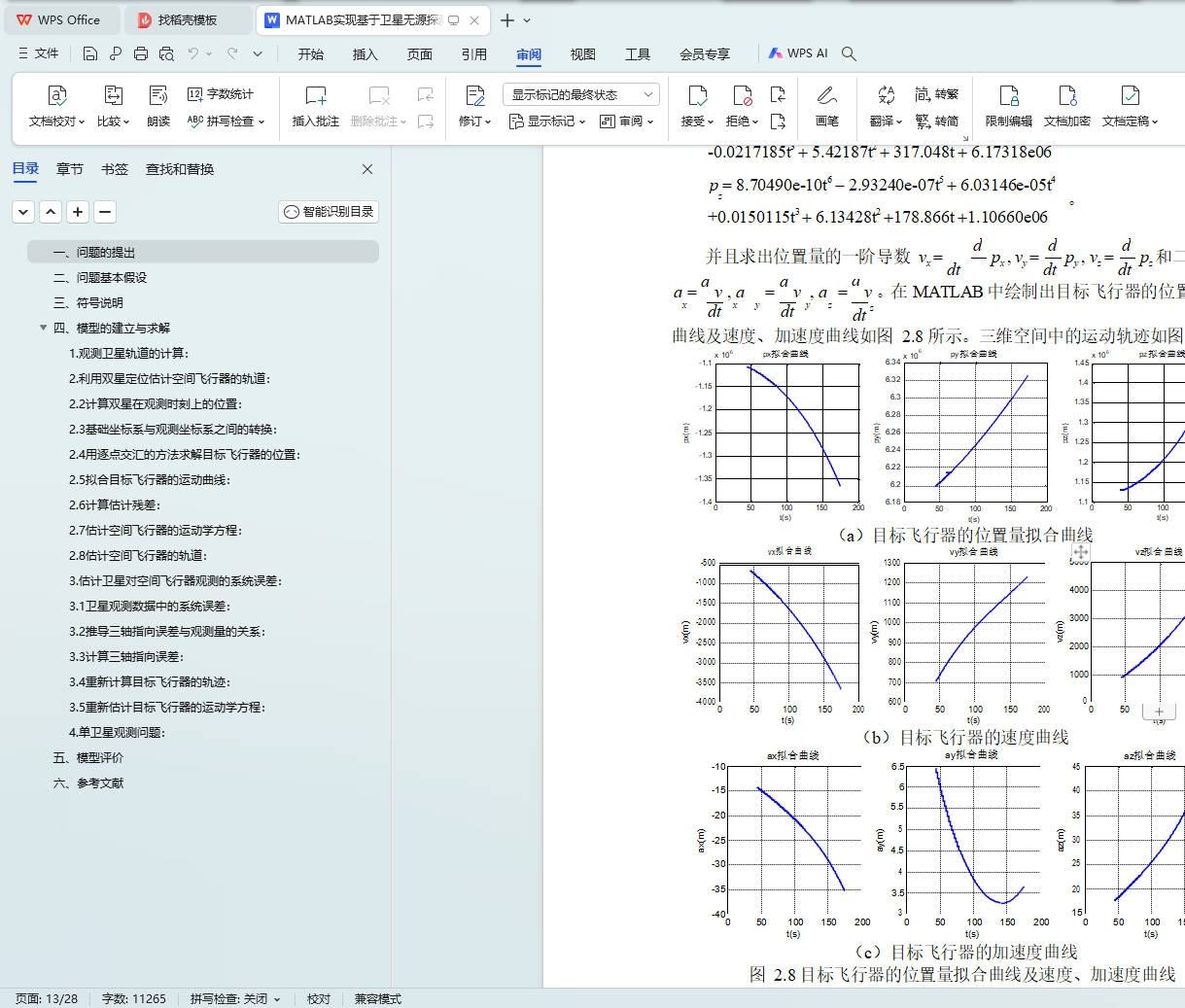
然后利用题目所提供的双星观测数据,按照逐点交汇的方法,初步得到空间飞行器的运行轨迹;接着拟合出一个平面,使得目标飞行器的轨迹点到该平面的距离最小,进而将轨迹点投影到该平面上,再对位置数据进行了拟合,并求出了位置、速度、加速度曲线;将位置量、速度、加速度带入到空间飞行器的运动方程中,估计出空间飞行器的运动模型,并得到了m(t) 的模型。
根据双星观测数据以及由模型反推出的观测量之间的偏差,估计出观测卫星的系统误差。我们经过公式推导发现,三轴指向误差与观测量偏差之间存在线性关系;因此采用最小二乘法对数据进行一次拟合,分别求出了两颗卫星的系统误差。然后消除观测量中的系统误差,重新求出了空间飞行器的轨迹,并拟合出位置、速度、加速度曲线,估计了空间飞行器的运动模型。
最后,我们对单卫星观测进行了设计,推导和利用空间飞行器轨迹的限制条件,缩小了轨迹的搜索区域,并提出了搜索轨迹的方案。
目录
一、问题的提出
二、问题基本假设
三、符号说明
四、模型的建立与求解
1. 观测卫星轨道的计算:
2. 利用双星定位估计空间飞行器的轨道:
2.2 计算双星在观测时刻上的位置:
2.3 基础坐标系与观测坐标系之间的转换:
2.4 用逐点交汇的方法求解目标飞行器的位置:
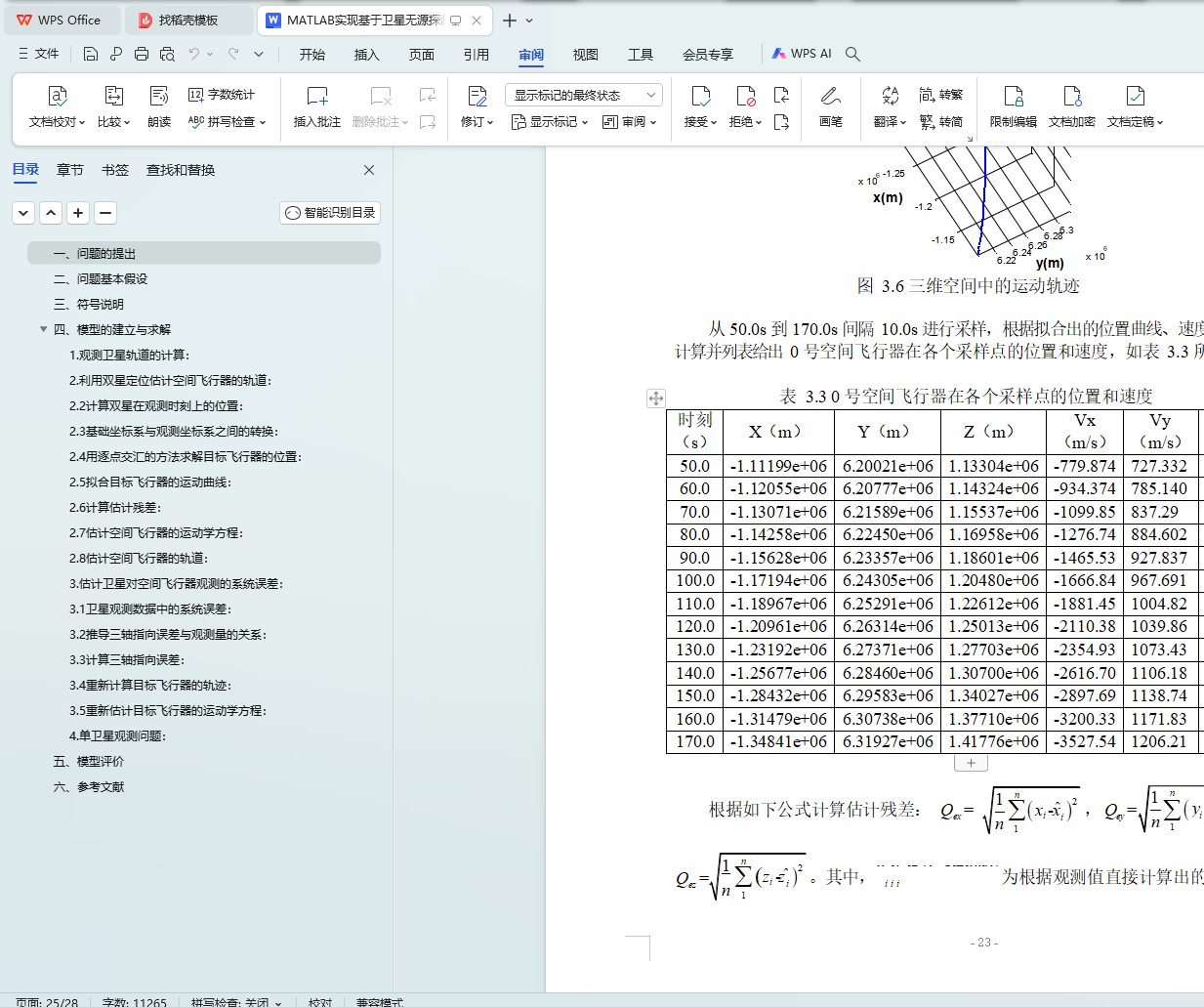
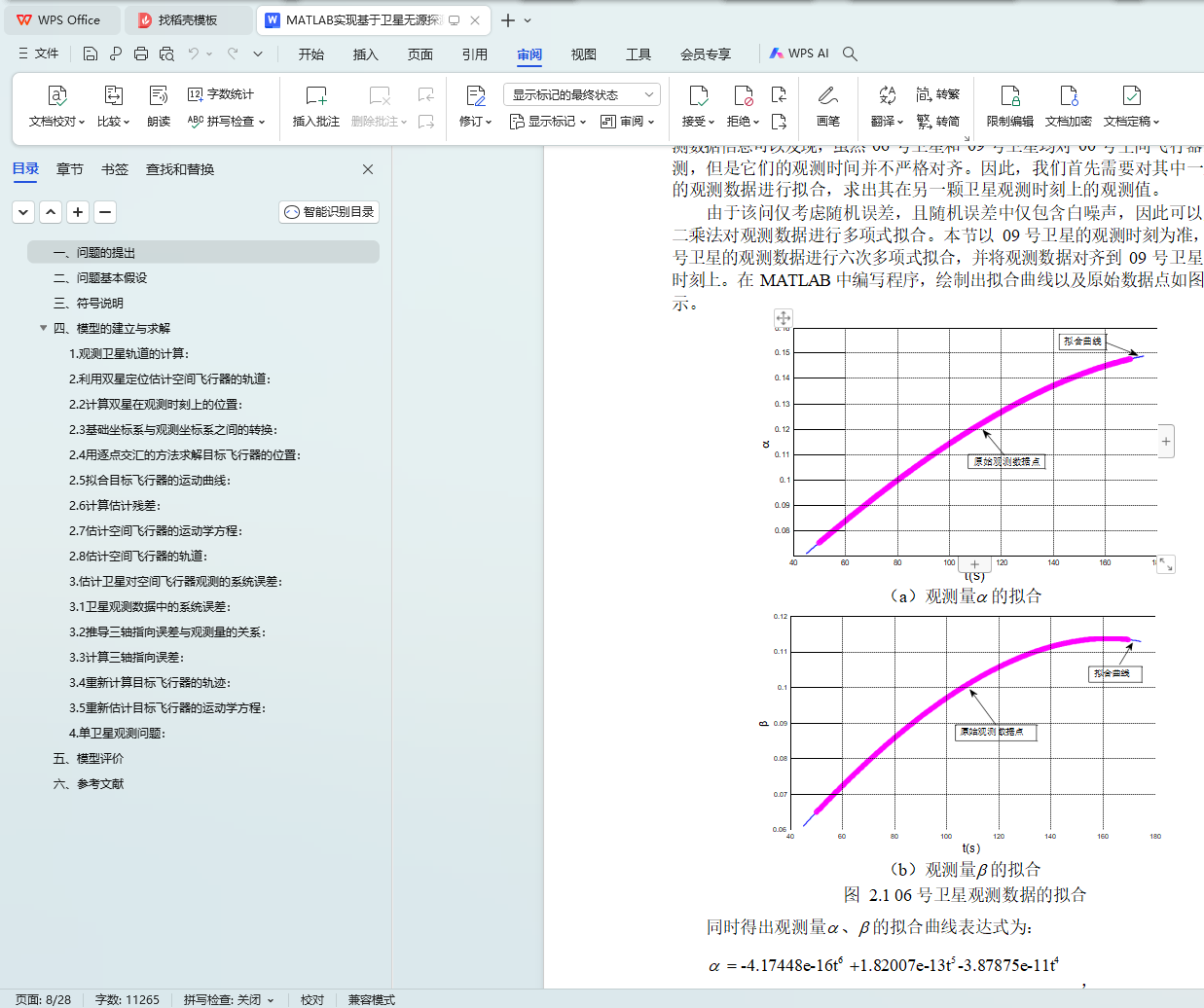
2.5 拟合目标飞行器的运动曲线:
2.6 计算估计残差:
2.7 估计空间飞行器的运动学方程:
2.8 估计空间飞行器的轨道:
3. 估计卫星对空间飞行器观测的系统误差:
3.1 卫星观测数据中的系统误差:
3.2 推导三轴指向误差与观测量的关系:
3.3 计算三轴指向误差:
3.4 重新计算目标飞行器的轨迹:
3.5 重新估计目标飞行器的运动学方程:
4. 单卫星观测问题:
五、模型评价
六、参考文献