题 目 基于伴随同化方法的空间飞行器轨道估计与误差分析
摘 要:
利用观测卫星获得的空间飞行器的轨道参数,结合动力学方程对空间飞行器的轨道进行估计,能够为飞行器类别、飞行意图的判断提供信息基础。
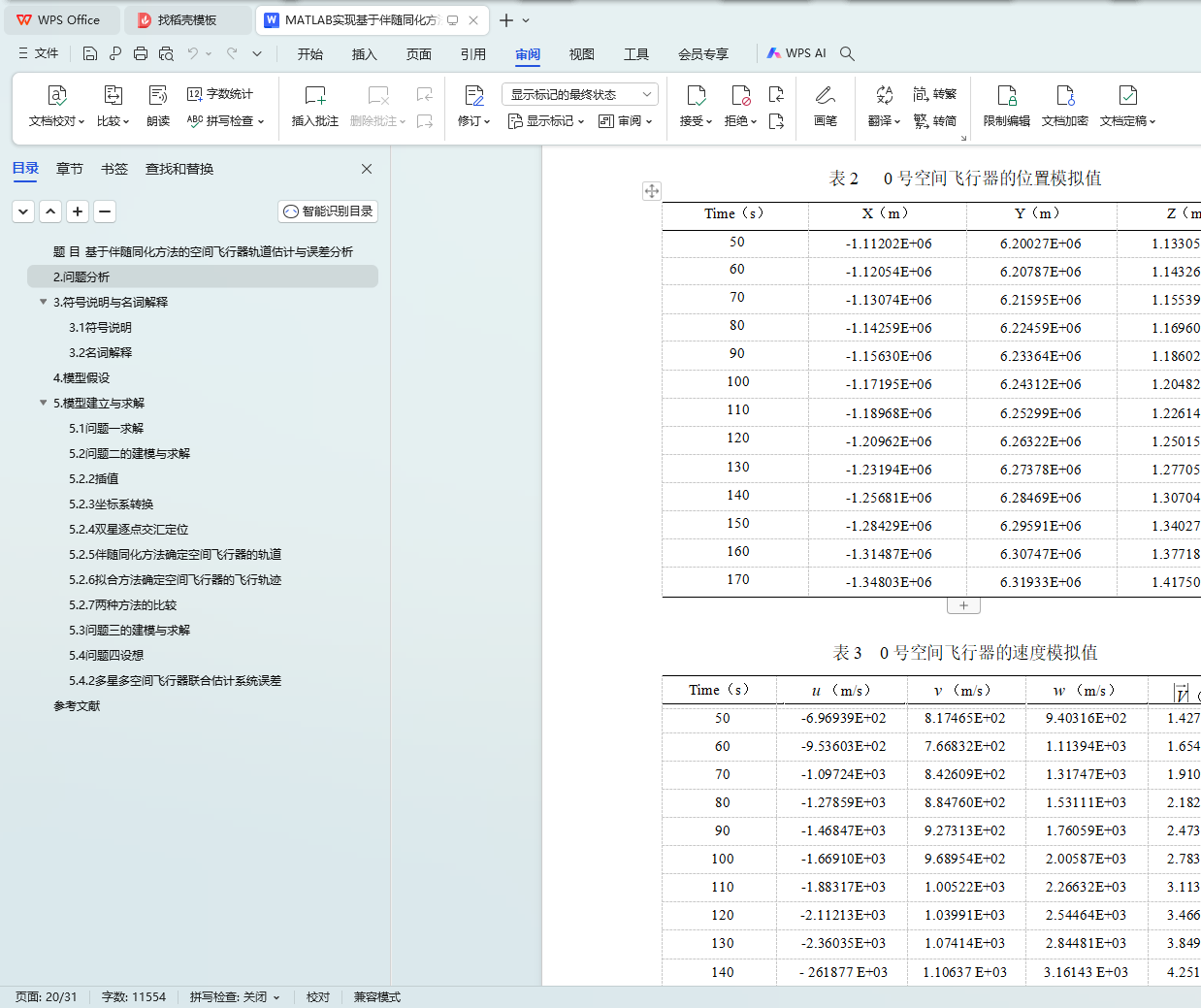
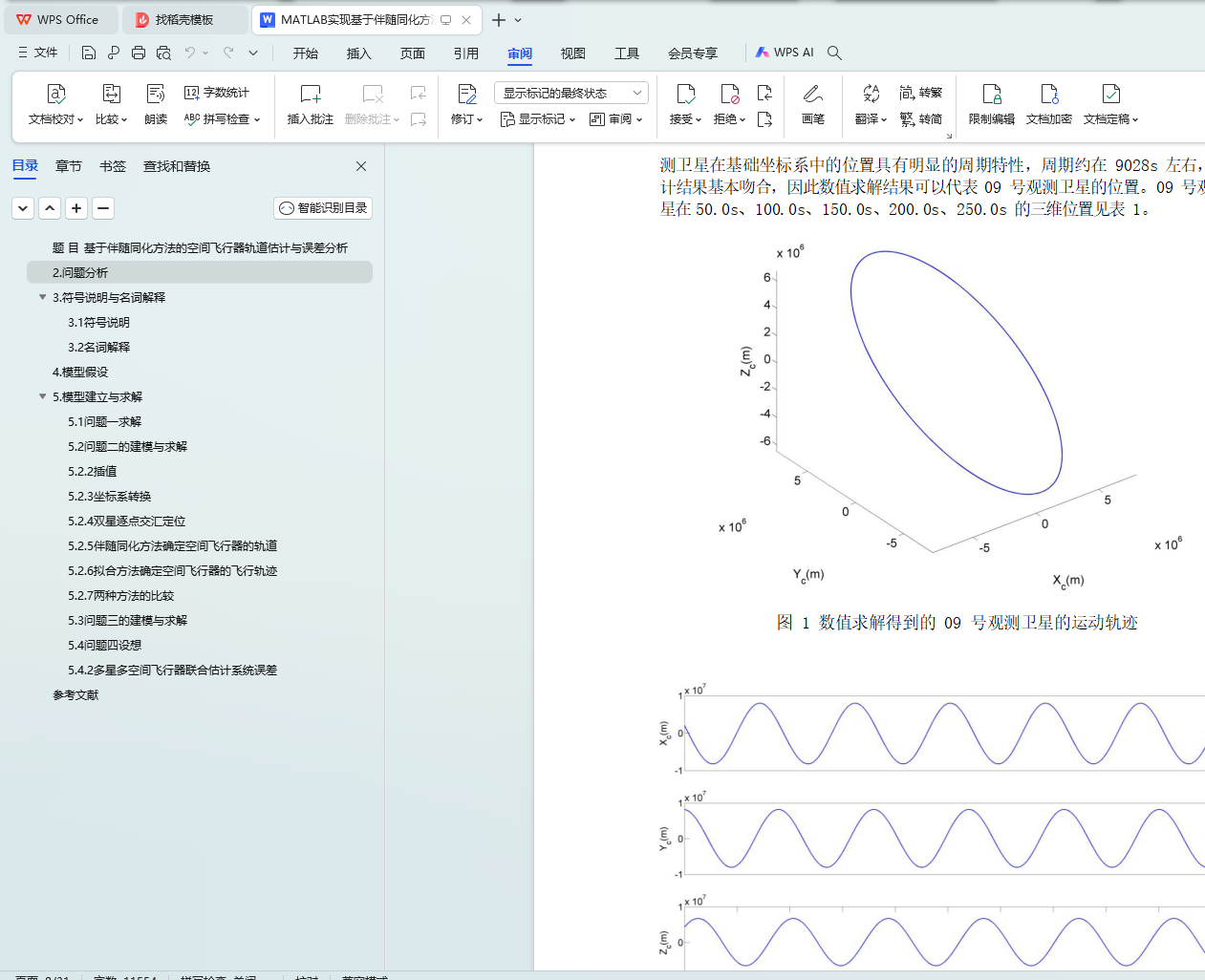
问题一对观测卫星的三维位置估计是基于卫星简化运动方程,利用观测卫星零时刻的位置和速度作为初始条件对运动方程数值求解, 得到观测卫星的运动轨迹,并得出观测卫星运行周期。通过与中低轨近圆轨道卫星运行轨迹和周期的对比,验证了计算结果的准确性。
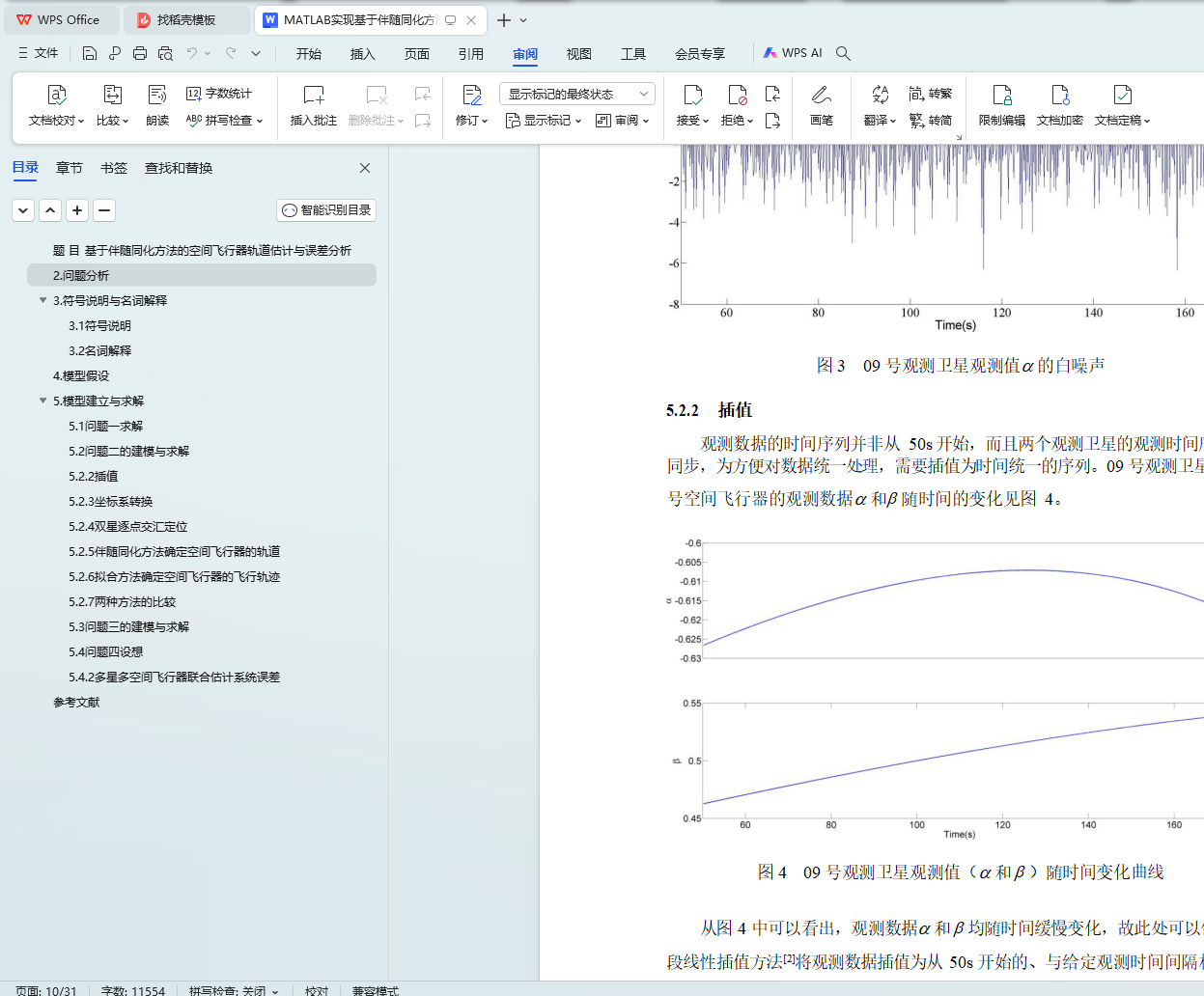
问题二中 06 号和 09 号观测卫星对 0 号空间飞行器的观测数据时间不同步而且数据中包含了随机误差(白噪声),故首先利用低通滤波器对观测数据进行滤波处理,再将观测数据插值为时间统一的序
列。然后将观测坐标系下的观测数据转化到基础坐标系中,根据逐点交汇定位的思路,计算出空间飞行器的所在位置。在此基础上,分别利用伴随同化方法和数据拟合方法给出了空间飞行器的位置和速度, 并给出位置的估计残差。两种方法得到的结果均与观测数据吻合较好,使用伴随同化方法的误差比使用数据拟合方法的小一个量级。
问题三在前文基础上考虑系统误差对观测数据产生的影响,根据对系统误差的认识和模型假设,认为逐点交汇定位方法可以对系统误差进行估计,推导出了观测数据和系统误差之间的转化关系。利用最小二乘原理,结合观测数据得到系统误差(两颗卫星的da 、db 和dq )。利用系统误差对原观测数据进行校正后,采用伴随同化方法给出了空间飞行器的位置和速度估计,并计算了位置的估计残差。
目录
题 目 基于伴随同化方法的空间飞行器轨道估计与误差分析
2. 问题分析
3. 符号说明与名词解释
3.1 符号说明
3.2 名词解释
4. 模型假设
5. 模型建立与求解
5.1 问题一求解
5.2 问题二的建模与求解
5.2.2 插值
5.2.3 坐标系转换
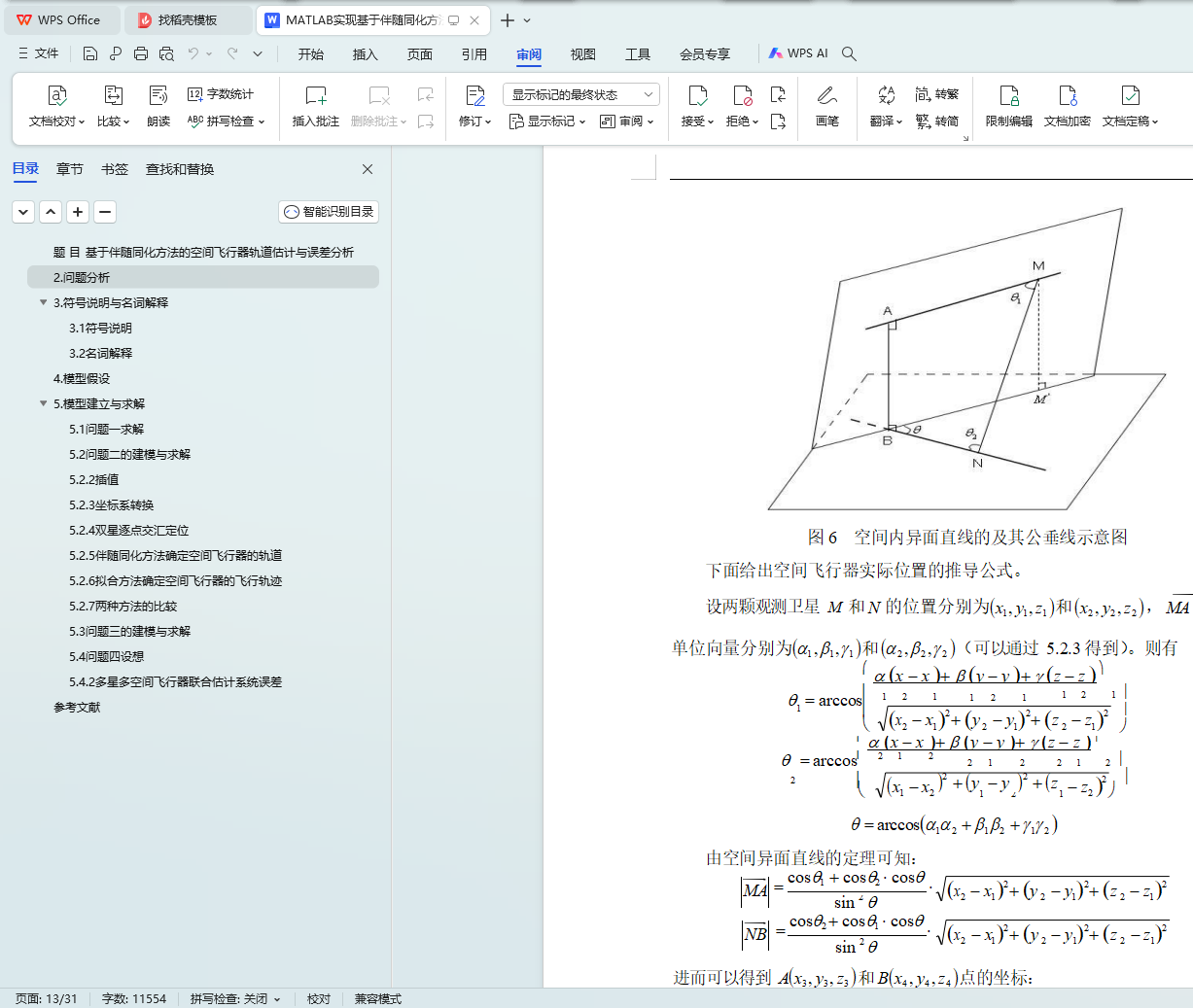
5.2.4 双星逐点交汇定位
5.2.5 伴随同化方法确定空间飞行器的轨道
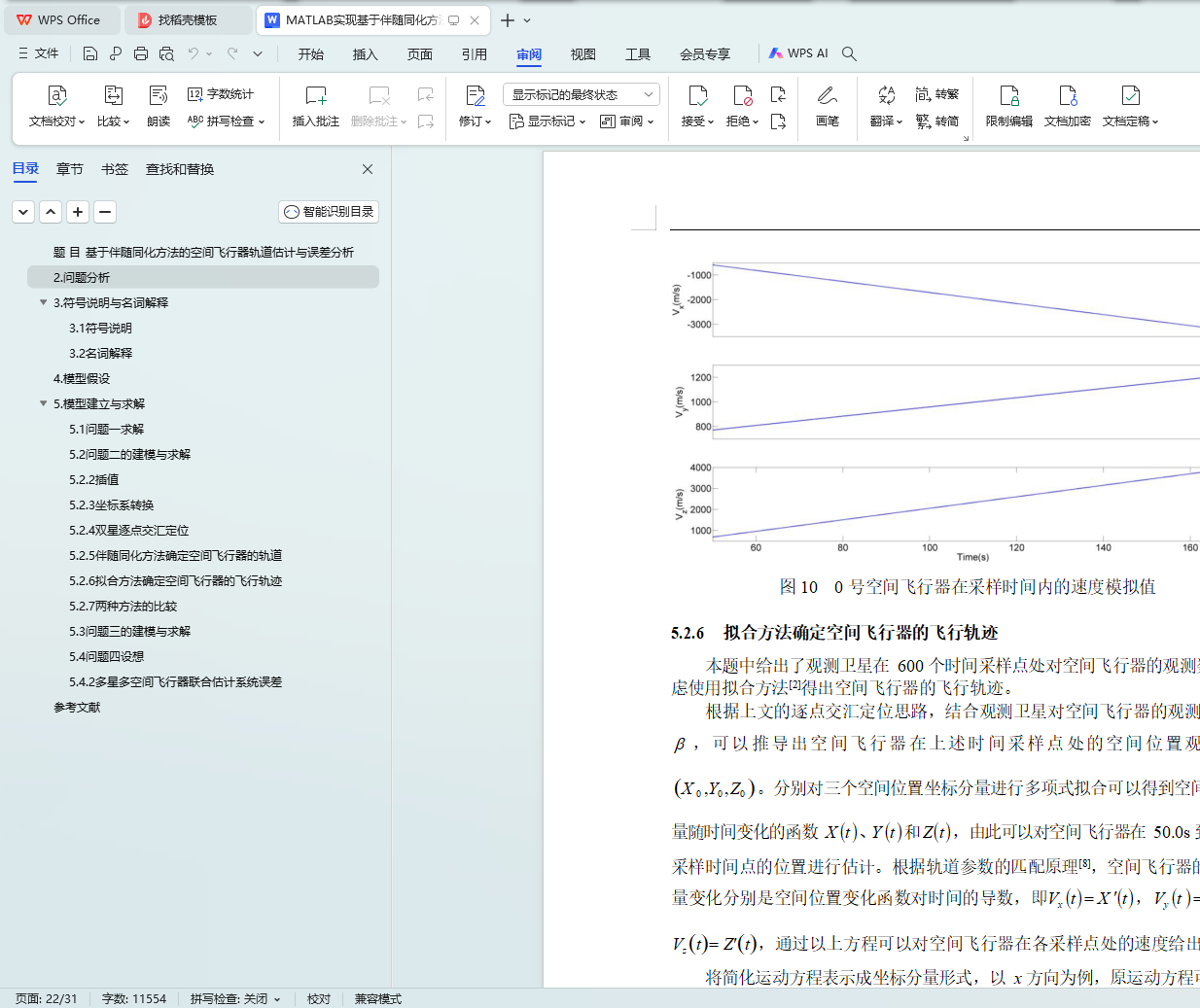
5.2.6 拟合方法确定空间飞行器的飞行轨迹
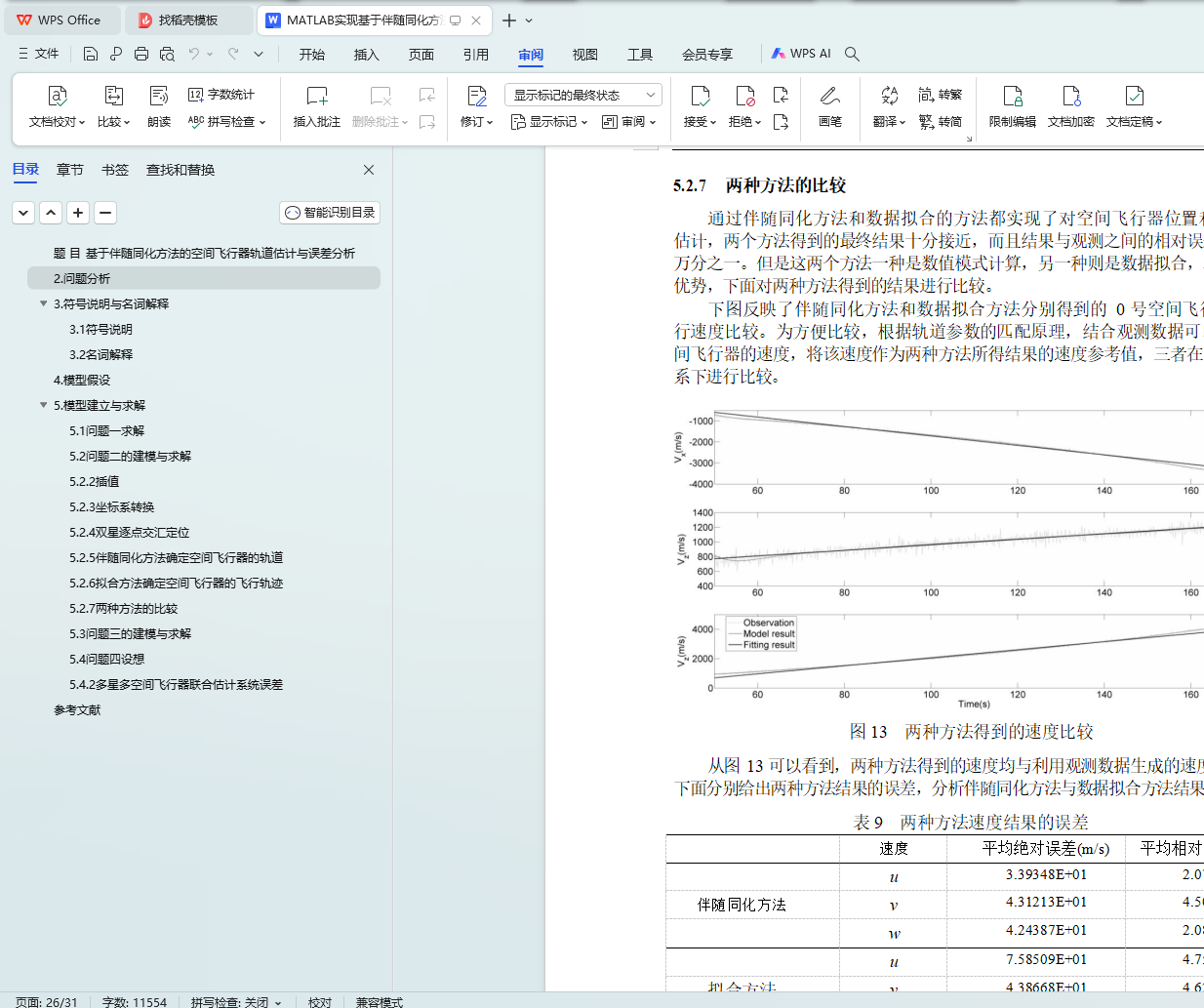
5.2.7 两种方法的比较
5.3 问题三的建模与求解
5.4 问题四设想
5.4.2 多星多空间飞行器联合估计系统误差
参考文献