题 目 与封堵溃口有关的封堵物落水后运动过程的数学模型研究
题 目 与封堵溃口有关的封堵物落水后运动过程的数学模型研究
摘 要:
本文针对落水后的封堵物,从受力角度出发,利用小型试验数据和系统辨识理论, 建立了封堵物落水后运动过程的数学模型。并据此模型和相似准则对封堵物的投放位置进行了预测以确保封堵物沉底到预定位置。
对于问题一,通过查阅文献和物理书籍,确定了影响封堵物在水中运动过程的因素,并对所有的小型试验数据进行统计分析、校正获得有效数据。然后依据牛顿运动定律和流体力学知识建立系统的模型结构;根据大实心方砖小型试验的有效数据,利用参数辨识获得最优参数值,最终建立了大实心方砖落水后运动过程的数学模型。
对于问题二,首先对问题一中的数学模型进行分析,确定所要求解的部分隐性影响因素,通过数据分析得到这些影响因素与物体运动模型参数见的关系,从而建立具有普适性的、描述封堵物水下运动过程的数学模型。
对于问题三,将建立模型的运动轨迹与小型试验所得轨迹进行比较,所得误差较小,验证了模型的合理性、有效性。在水深、水流速、投放高度已知的前提下,基于模型猜想封堵物恰好在最有效位置触底与投掷点与溃口的水平距离有关。
对于问题四,1、小型试验满足重力相似准则。根据试验与实际情况确定长度比尺,然后根据对流动受力情况,满足对流动的主要作用力相似,选择重力相似准则。通过选定的长度比尺和相似准则,确定各物理量的比尺,这样小型试验的结果就可以推广到真实情况。2、水深 3m 和 4m,流速 4m/s 和 5m/s 时,分别提前 0.244m 和 1.06m 投放。
关键词:封堵物落水运动过程模型 二分法 参数识别 相似准则
目录
一.问题的重述
二.问题的假设
三.符号说明
4.1 问题分析
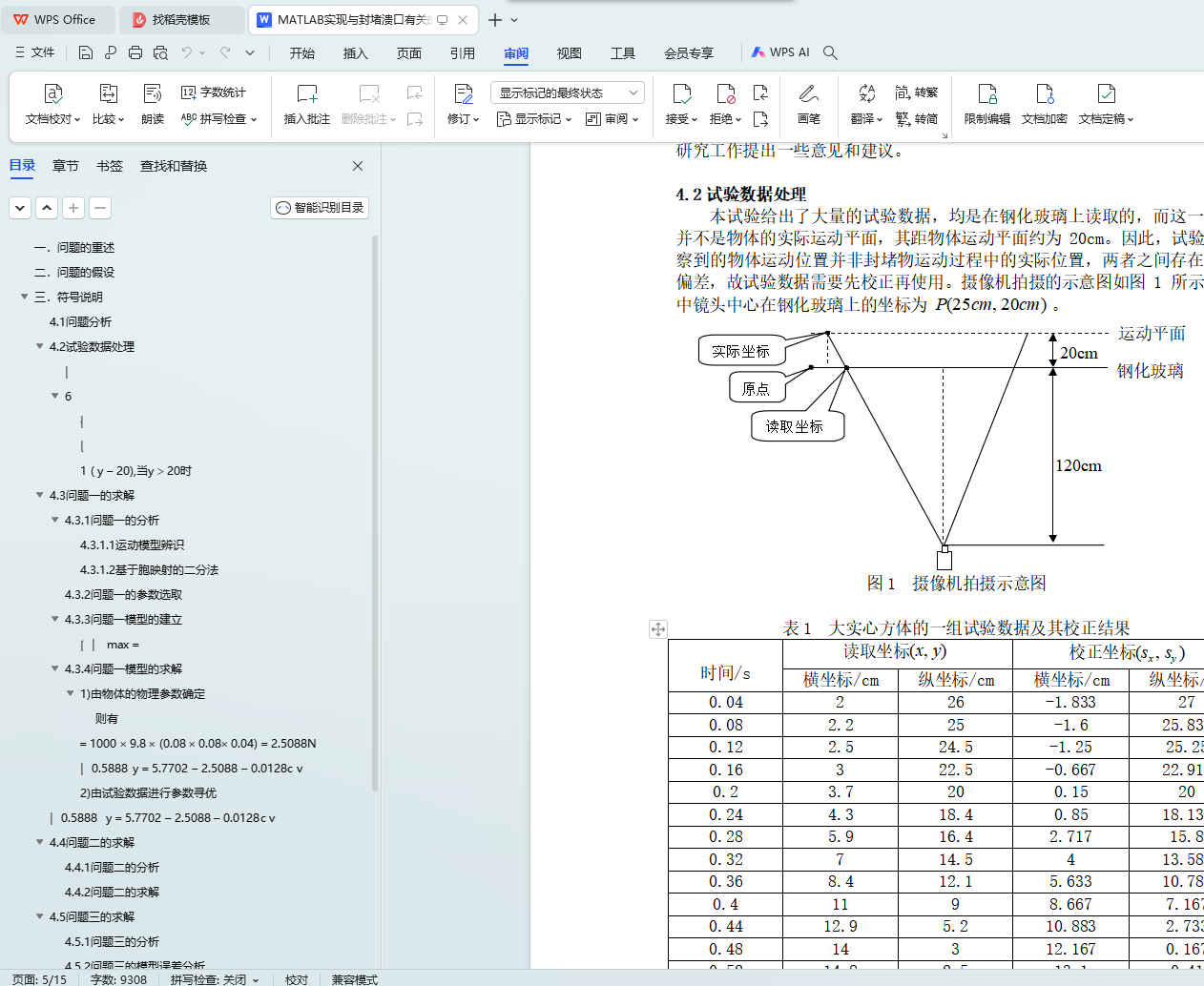
4.2 试验数据处理
⎪
6
4.3 问题一的求解
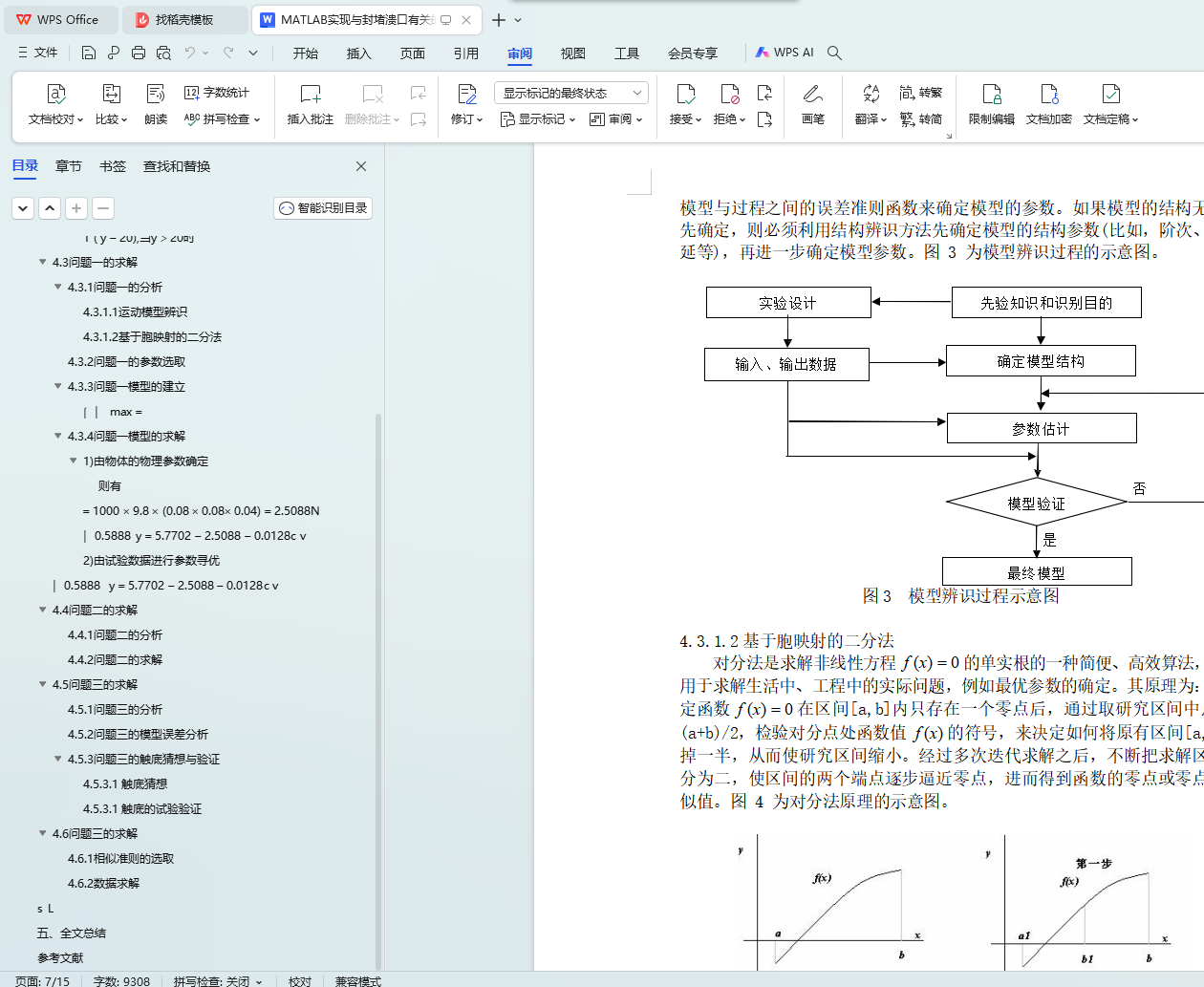
4.3.1 问题一的分析
4.3.2 问题一的参数选取
4.3.3 问题一模型的建立
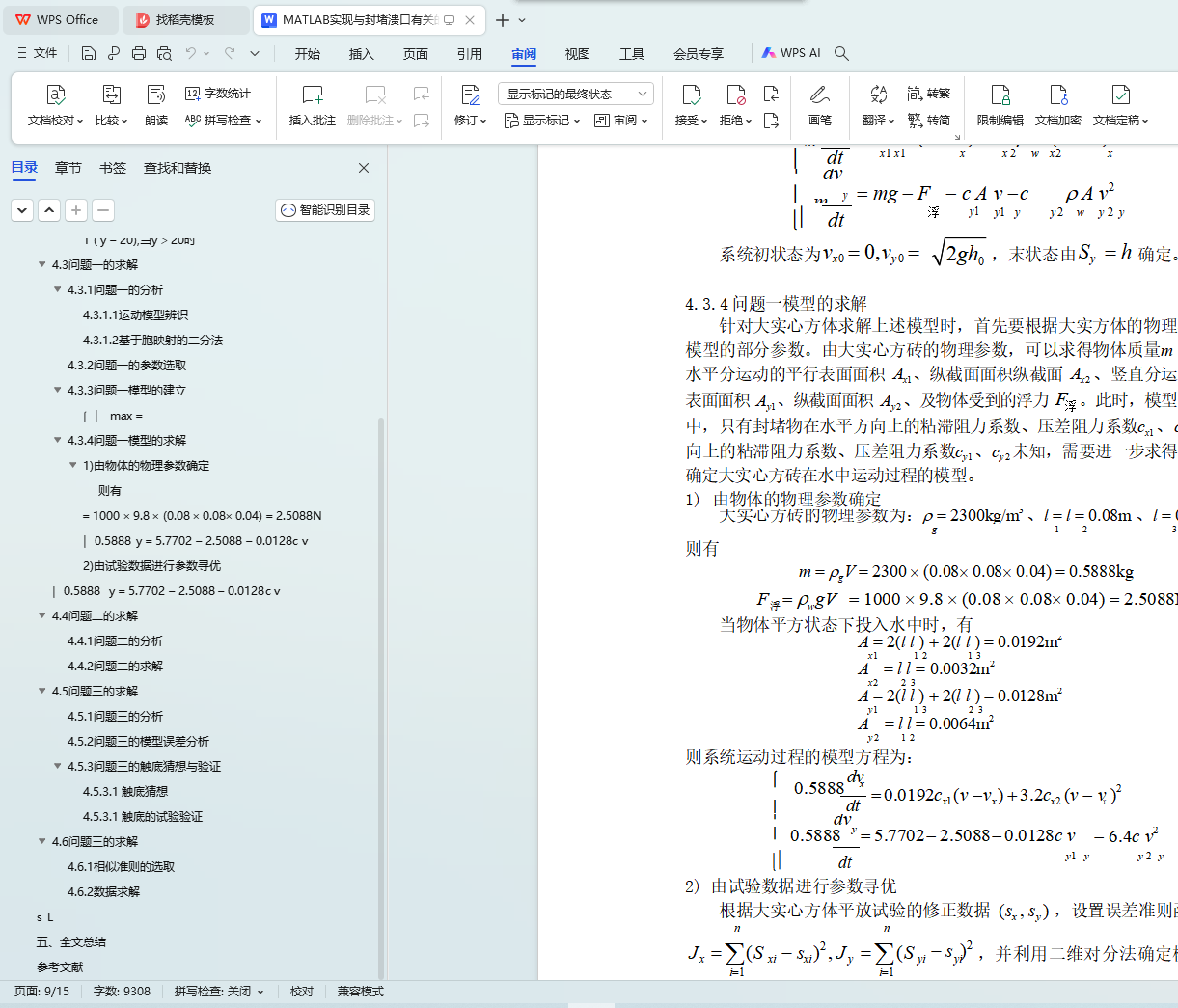
4.3.4 问题一模型的求解
⎪0.5888 y = 5.7702 - 2.5088 - 0.0128c v
4.4 问题二的求解
4.4.1 问题二的分析
4.4.2 问题二的求解
4.5 问题三的求解
4.5.1 问题三的分析
4.5.2 问题三的模型误差分析
4.5.3 问题三的触底猜想与验证
4.6 问题三的求解
4.6.1 相似准则的选取
4.6.2 数据求解
s L
五、全文总结
参考文献