激活函数可调的神经元网络的一种快速算法

沈艳军 汪秉文

（华中科技大学控制科学与工程系,武汉,430074）

目录

激活函数可调的神经元网络的一种快速算法

摘要

关键词 神经网络，RLS算法，神经元模型，学习算法

前言

1 TAF模型以及多层前向TAF网络

2 TAF多层前向神经网络(TAF-MFNN)的一种快速学习算法

3  模拟实验与仿真结果

3.1 XOR问题

网络输出是

3.2 非线性函数逼近

用于训练网络的数据被定义为

3.3 逼近非线性多维函数

4 多层前向TAF网络的改进

5 结论

参考文献

摘要

    本文提出了一个具有激活函数可调的神经元网络的改进结构,给出了神经网络学习的一种快速算法。XOR问题, Feigenbaum函数和Henon映射的仿真结果表明, 新算法比BP（向后传播）算法具有很短的收敛时间和很高的收敛精度。具有更快学习算法的神经网络结构的进一步改进演示了具有更快收敛速度和更好收敛进度的简单结构。

   关键词 神经网络，RLS算法，神经元模型，学习算法

前言

神经网络及其相关技术是强大的工具,提供了在现实世界的工程应用中的高效性,如联想记忆、组合优化问题,系统辨识和自适应控制、预测、语音识别、以及信号处理。人工神经网络的研究可以追溯到1940年。M-P模型是W.C.McCulloch和数学家W.Pitts于1943年提出的。在各种人工神经网络的研究中得到广泛的应用。在这个模型中，连接权值和非线性激活函数分别模仿神经元的突触和细胞体的功能。在训练过程中，权值是可调的，但激活函数是固定的。显然，这种模型过于简单，和生物神经元不同，其性能受到极大的限制。人工神经网络的研究在过去的五十年取得很大的进步。然而，一些问题暴露出来，阻碍了研究工作的进展。这三个问题总结如下^[1]：

（1）因为M-P模型的激活函数固定不变，所以不适合某些问题的求解。Segee等对一些普通有用的BP网络有深入理解。他发现,当采用固定的S-型激活函数神经细胞网络来解决一些问题时，很难得到满意的结果,因为网络收敛速度非常慢，而且对某些参数变化过于敏感。Segee^[2]的结论具有启发意义.基于有关采用s-型、Gauss型和正弦型激活函数的神经网络模型的映射能力的模拟实验，Lee和Kil^[3]等人发现在这三种网络中采用s-型激活函数的网络映射能力最差。

（2）网络的容量与网络的规模有关。一般来说，解决较复杂的问题时需要采用规模较大的网络。然而，人工神经网络的设计目前还缺少系统的理论来指导。通常是根据研究人员的经验，先选用某一合适的网络结构，再依靠试错法来决定较好的网络。如果网络结构和规模选择不当，则训练将十分困难。因此，如何设计所需的网络，依然是一个未解决理论问题。

（3）在设计网络时，引入先验知识可以使网络结构大大简化，但是如何把先验知识引入网络设计还是一个公开问题。Stork等曾利用先验知识来选择神经网络的激活函数，使网络大大简化。为了解决N-位奇偶校验问题，他们采用一种特殊的非线性函数作为激活函数，仅需要2个隐层单元^[4-5]。Wu Youshou等从理论上研究了这个问题^[6-7]，他们利用待解决问题的先验知识来确定激活函数，得到很有意义的结果。例如，使用仅含一个隐层单元的BP神经网络，诸如N位奇偶校验和N编码问题就可被解决。

在M-P的传统模型中，神经细胞之间的连接被认为是能够储存信息的、可调节的。但模拟细胞体的激活函数是固定的。它的作用是只对激活信号进行非线性处理。显然，这种模型过于简单。人工神经网络在众多很困难的问题上失败的原因很可能是这个模型的简单性。事实上，生物神经元的类型是多种多样的。处理不同的信息的神经元也是多种多样的。基于这个假设，吴佑寿等^【8-9】提出一种激活函数可调的多层前馈神经网络（TAF-MFNN）。它的学习算法是反向传播（BP）算法。若干实验表明，对比MFNN, TAF-MFNN可以较容易地解决困难的问题，简化网络结构并且有优良的网络性能和泛化能力。

然而，众所周知BP算法是一种古典算法和一种用于对一个特定网络输入最小化期望输出和实际输出之间的均方误差的迭代梯度算法。尽管它成功地应用于很多情形，但是BP还是有很多缺点。一个缺点在于算法收敛速度。对甚至是很简单的问题，都需要多次迭代。根据求和（非线性层的输入），RLS算法^[12-14]利用改进的BP算法去最小化期望输出和实际输出之间的均方误差。这一点和根据权值最小化均方误差的标准BP算法不同。由反向传播算法产生的误差信号被用于估计求和输出的值，将改善网络总误差。这些估计连同相应节点的输入向量，通过在每个节点上的一个线性方程系统，被用于产生一个权重的更新设置。用在每层上的Kalman滤波器，可解这些线性方程的系统。训练模式运行于整个网络直到收敛。 

基于此，我们改进了TAF神经模型的结构并提出了一个训练神经网络的快速学习算法。XOR问题，Feigenbaum函数和Henon映射的仿真结果, 在收敛时间短和较高的收敛精度方面，新算法具有比BP算法更好的性能。关于具有更快的学习算法的神经网络结构的进一步改进的实验演示了收敛速度更快、收敛精度更好的简单结构。

1 TAF模型以及多层前向TAF网络

TAF模型如图1所示。在这个模型中，一个神经细胞被分为两部分：突触和细胞体。前者的作用是将一个多维信号映射到另一个多维信号：S=g(X,W),其中S被称为“内部激活”, 是细胞体的输入信号。胞体的功能是非线性地变换内部激活。它的输出是O,O=f(S，α)，其中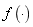是一个非线性函数，称为可调激活函数（TAF）。在这个函数中，α是一个可调参数。通过调整α，可以通过训练来改变，从而适应该问题。

图1普通TAF模型

TAF模型给出了一般形式：