表 2.1	数据变量介绍. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	7
表 2.1	Variables introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	7
表 2.2	各变量统计特征. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	7
表 2.2	Summary of variables. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	7
表 2.3	划分数据集. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	8
表 2.3	Partition dataset. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	8
表 2.4	标准化训练集. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	8
表 2.4	Standardize training set.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	8
表 5.1	MCMC 方法运行结果. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	20
表 5.1	Result of MCMC method. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	20
表 5.2	MCMC 方法区间估计. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	20
表 5.2	Interval estimation using MCMC method. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	20
表 5.3	MCMC 方法参数估计标准误. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	21
表 5.3	Estimation standard error using MCMC method. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	21
表 5.4	INLA 运行结果. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	22
表 5.4	Result of INLA method. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	22
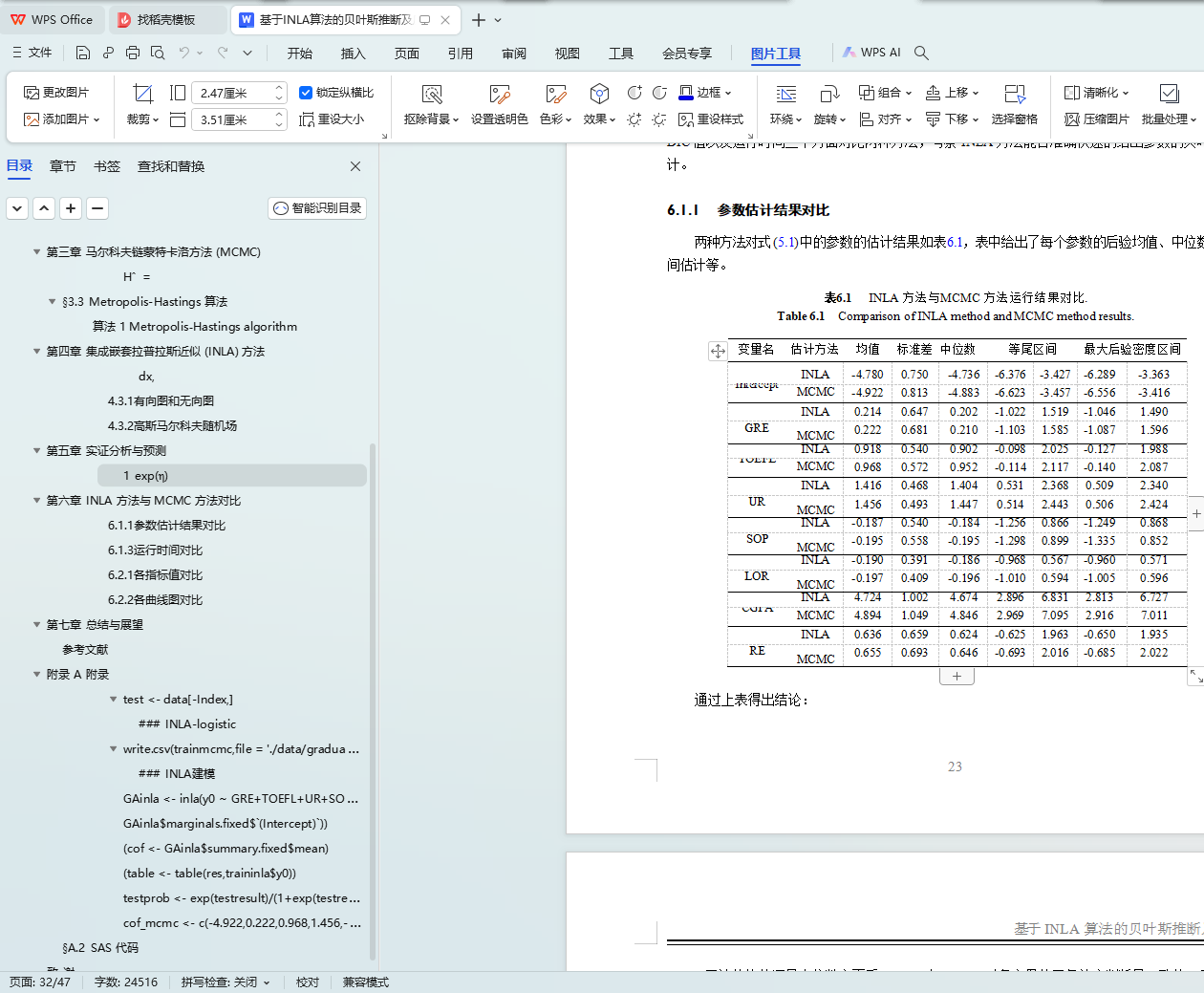
表 6.1	INLA 方法与 MCMC 方法运行结果对比. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	23
表 6.1	Comparison of INLA method and MCMC method results. . . . . . . . . . . . . . . . . . . . . . . . . . . .	23
表 6.2	INLA 方法与 MCMC 方法的 DIC 值. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	24
表 6.2	DIC value of INLA method and MCMC method. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	24
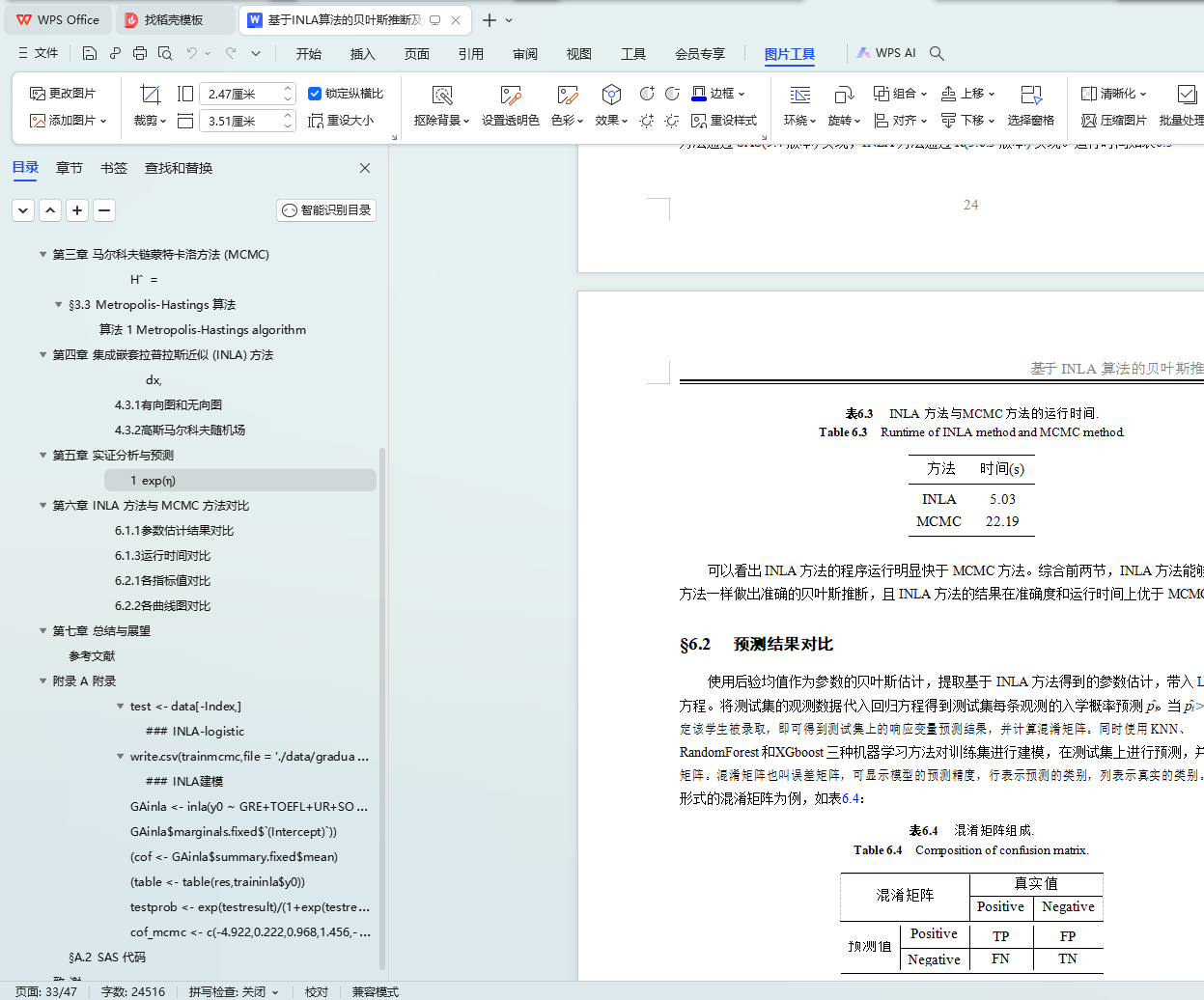
表 6.3	INLA 方法与 MCMC 方法的运行时间. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	25
表 6.3	Runtime of INLA method and MCMC method. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	25
表 6.4	混淆矩阵组成. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	25
表 6.4	Composition of confusion matrix. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	25
表 6.5	各方法混淆矩阵. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	26
表 6.5	Confusion matrices of each method. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	26
表 6.6	模型评价指标比较. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	26
表 6.6	Comparison of model evaluation indices. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	26

摘要

在贝叶斯理论中，我们将参数视为随机变量并具备先验分布，将先验与现有数据的似然结合得到后验分布并进行参数推断，因此计算后验分布的积分是关键。然而实证中的后验分布往往是高维的，使得传统计算方法无法得到理想结果。随着近代计算机科学的发展，马尔科夫链蒙特卡洛 (MCMC) 方法产生，MCMC 方法通过构造马尔科夫链，使其收敛后的平稳分布为待积后验分布，得到后验分布的经验样本，进而可以准确的得到参数估计。然而，当前的世界已经逐步进入了大数据的时代，数据在时间和空间上的结构复杂性大大增加了

MCMC 方法的时间成本，这也限制了 MCMC 方法在实际中的应用。

在此之前，拉普拉斯近似也可以计算后验积分，对被积函数在峰值点进行二阶泰勒展开并作高斯近似，以得到被积函数的积分近似。但随着 MCMC 方法出现，此方法逐渐失去了关注度。本文引用 Rue 等基于拉普拉斯近似提出的进行贝叶斯推断的新方法——集成嵌套拉普拉斯近似 (INLA) 方法。INLA 方法作用于属于高斯马尔科夫随机场的隐高斯模型，将拉普拉斯近似与数值积分结合，超参数分布近似使用拉普拉斯近似，再利用数值积分得到参数的后验边际，进而做出较为精确的推断，且运算效率远高于 MCMC 方法。

本文使用预测研究生录取的数据集，建立 Logistic 回归模型，并对参数分别进行基于

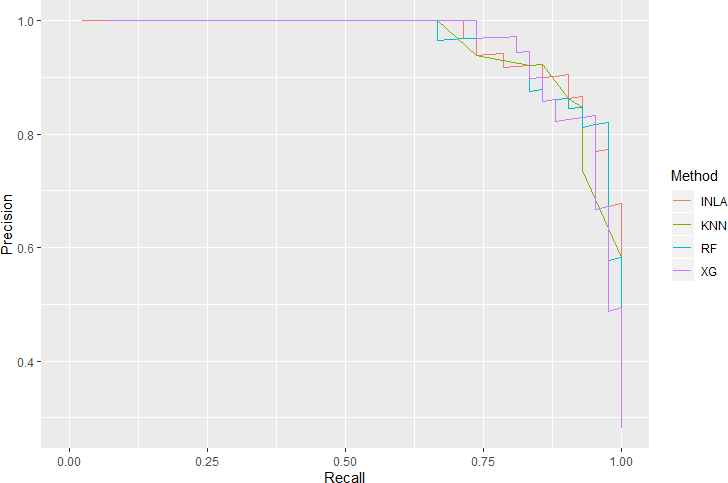
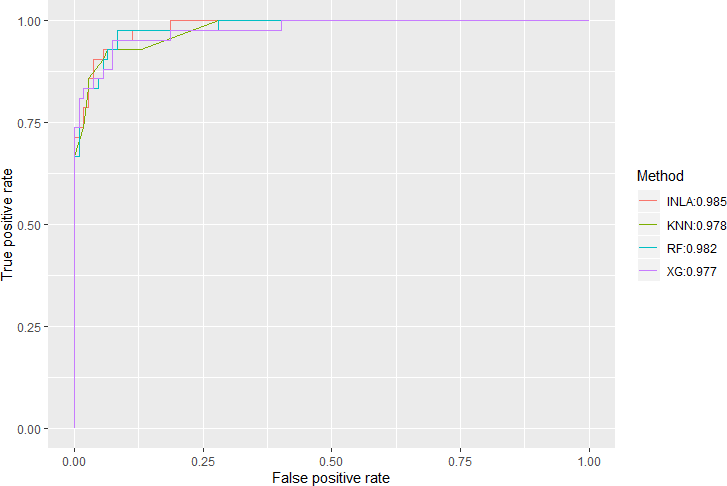
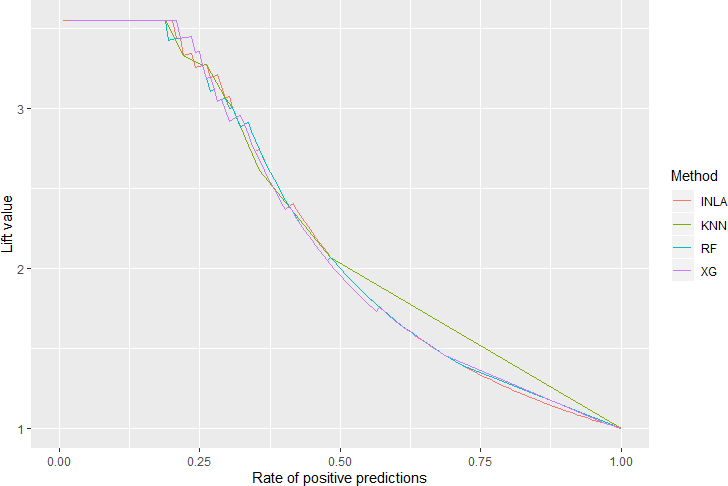
MCMC 和 INLA 方法的贝叶斯推断。使用 SAS 和 R 分别完成 MCMC 方法和 INLA 方法的实现，并从参数估计结果、运行时间和 DIC 值三个方面对两种方法进行比较。结果显示 INLA 方法可以得到精确的参数估计，且在运行时间方面明显优于 MCMC 方法，这说明了 INLA 方法对参数的贝叶斯推断有十分理想的效果，对 MCMC 方法也有很好的的替代性。本文最后使用参数估计结果代入模型对测试集进行预测，同时使用 KNN、随机森林和 XGboost 三种机器学习算法建模，并从混淆矩阵、衍生指标 (准确率、Kappa 值和 AUC 值等) 和曲线

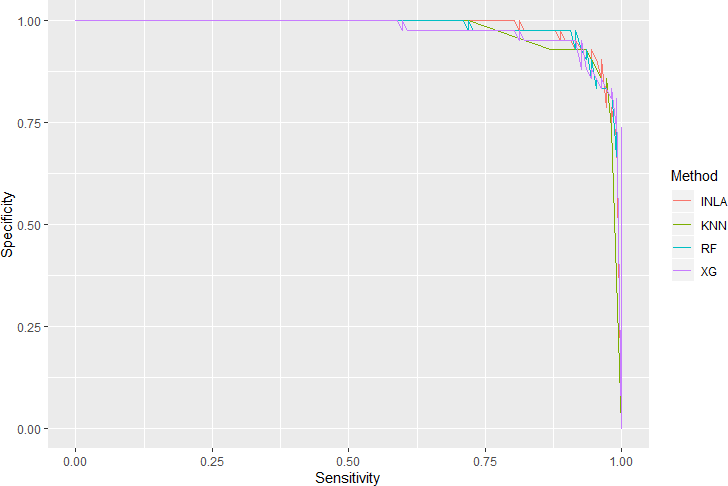
(ROC 曲线、提升图等) 三个方面对比模型预测效果，结果显示基于 INLA 方法估计参数的

Logistic 回归模型具备较好的预测效果，并不逊于这三种机器学习算法。

关键词: INLA，MCMC，拉普拉斯近似，Logistic 回归，DIC，机器学习

Abstract

In Bayesian theory, we treat the parameters that have a prior distribution as random variables. The inference of parameters is based on posterior distribution, which is obtained by combining likelihood from existing data and prior. Therefore, the key is to calculate the integral of poste rior distribution. However, in the past, statistical analysis based on the Bayes theorem was often daunting as the posterior distribution is often in a space of high dimension. With the development of modern computer science, for many years, Bayesian inference has relied upon Markov chain Monte Carlo method to compute the posterior distribution. The MCMC method constructs a Markov chain so that the stationary distribution of this chain when converged is the posterior distribution, then we get empirical samples of posterior, which can accurately obtain the estimates of parameters. However, with the advent of big data era, the structural complexity of data in time and space has greatly increased the time cost of MCMC method, which also limits its application.

Before that, there is a Laplace approximation method that can also calculate posterior integral, by performing a secondorder Taylor expansion of integrand at the peak point and make a Gaussian approximation to obtain an integral approximation of the integrand. However, with the emergence of MCMC method, this method gradually lost focus. This paper cites a novel approach for Bayesian inference proposed by Rue et al: the integrated nested Laplace approximation (INLA) method. The INLA method focuses on latent Gaussian model that can be expressed as latent Gaussian Markov random fields (GMRF). It combines the Laplace approximation with numerical integration. The ap proximation of hyperparameter distribution uses the Laplace approximation, and we use numerical integration to obtain the posterior marginal distribution for further inference of parameters, which

is more efficient than the MCMC method.

In this paper, we use a dataset for prediction of Graduate Admissions to establish a Logistic regression model, and perform Bayesian inference for the parameters based on MCMC and INLA method respectively. Use SAS and R to complete the implementation of MCMC and INLA method respectively, and compare the two methods from parameter estimation results, program running time and DIC value. The result shows that the INLA method can obtain an accurate parameter estimation, and is significantly better than the MCMC method in terms of running time. This shows that the INLA method can be regarded as a valid alternative to the MCMC method. Finally, we model a Logistic regression using the parameter estimation results from INLA method to forecast the test set. Furthermore, we use three machine learning algorithms (KNN, random forest and XGboost) to model and forecast, and compare these four methods from derived indicators (accuracy rate, Kappa value and AUC value, etc.) calculated from confusion matrix and curves (ROC curve, lifting chart, etc.). Results show that the Logistic regression model with parameters estimated by INLA method also has good predictive effect, which is not inferior to these three machine learning algorithms.

目 录

摘 要

is more efficient than the MCMC method.

目录

摘要