2设计问题一：基于SAT的数独游戏求解程序

2.1 问题概述

SAT问题即命题逻辑公式的可满足性问题（satisfiability problem），是计算机科学与人工智能基本问题，是一个典型的NP完全问题，可广泛应用于许多实际问题如硬件设计、安全协议验证等，具有重要理论意义与应用价值。SAT问题也是程序设计与竞赛的经典问题。

对于任一布尔变元x，x与其非“¬x”称为文字(literal)。对于多个布尔变元，若干个文字的或运算l1∨l2∨…∨lk称为子句(clause)。只含一个文字的子句称为单子句。不含任何文字的子句称为空子句，常用符号□表示。子句所含文字越多，越易满足，空子句不可满足。

SAT问题一般可描述为：给定布尔变元集合{x1, x2, ..., xn}以及相应的子句集合{c1, c2, ..., cm}，对于合取范式（CNF范式）：F = c1∧c2∧...∧cm，判定是否存在对每个布尔变元的一组真值赋值使F为真，当为真时（问题是可满足的，SAT），输出对应的变元赋值（一组解）结果。

一个CNF公式也可以表示成子句集合的形式：S={c1,c2,...,cm}.

例如，由三个布尔变元a,b,c所形成的一个CNF公式（¬a∨b）∧（¬b∨c）,可用集合表示为{¬a∨b,¬b∨c}，该公式是满足的，a=0, b=0,c=1是其一组解。

一个CNF SAT公式或算例的具体信息通常存储在一个.cnf文件中，下图2.1是算例problem1.cnf文件前若干行的截图。

图2.1 cnf文件格式

在每个cnf文件的开始，由‘c’开头的是若干注释说明行；‘p’开头的行说明公式的总体信息，包括：范式为CNF；公式有200个布尔变元，由1到200的整数表示；320个子句。之后每行对应一个子句，0为结束标记。46表示第46号变元，且为正文字；-46则是对应的负文字，文字之间以空格分隔。

DPLL算法是经典的SAT完备型求解算法，对给定的一个SAT问题实例，理论上可判定其是否满足，满足时可给出对应的一组解。本设计要求实现基于DPLL的算法与程序框架，包括程序的改进也必须在此算法的基础上进行。

2.2 DPLL算法思想

DPLL算法是一种基于树的回溯算法，主要使用两种基本处理策略：

单子句规则。如果子句集S中有一个单子句L,那么L一定取真值，于是可以从S中删除所有包含L的子句（包括单子句本身），得到子句集S1，如果它是空集，则S可满足。否则对S1中的每个子句，如果它包含文字¬L,则从该子句中去掉这个文字，这样可得到子句集合S2。S可满足当且仅当S2可满足。单子句传播策略就是反复利用单子句规则化简S的过程。

分裂策略。按某种策略选取一个文字L.如果L取真值，则根据单子句传播策略，可将S化成S2；若L取假值（即¬L成立）时，S可化成S1.

根据上述规则可不断对公式化简，并最终达到终止状态，其执行过程可表示为一棵二叉搜索树,如下图2.2所示。

图2.2 DPLL算法搜索树

基于单子句传播与分裂策略的DPLL算法可以描述为一个如后所示的递归过程DPLL( S ),为了优化执行效率，一般用非递归实现。

DPLL( S) :

/* S为公式对应的子句集。若其满足，返回TURE；否则返回FALSE. */

{

while(S中存在单子句) {//单子句传播

在S中选一个单子句L；

依据单子句规则，利用L化简S；

if S = Φ return(TRUE);

else if (S中有空子句 ) return（FALSE）；

}//while

基于某种策略选取变元v；//策略对DPLL性能影响很大

if DPLL（S ∪v ）return(TURE);

return DPLL(S ∪¬v);

}

对于公式{¬1∨2, ¬3∨4, ¬5∨¬6, 6∨¬5∨¬2},大家可以利用DPLL算法进行手动推理其处理过程与求解结果。

2.3 功能要求

本设计要求精心设计问题中变元、文字、子句、公式等有效的物理存储结构，基于DPLL过程实现一个高效SAT求解器，对于给定的中小规模算例进行求解，输出求解结果，统计求解时间。要求具有如下功能：

⑴ 输入输出功能：包括程序执行参数的输入，SAT算例cnf文件的读取，执行结果的输出与文件保存等。(15%)

⑵ 公式解析与验证：读取cnf算例文件，解析文件，基于一定的物理结构，建立公式的内部表示；并实现对解析正确性的验证功能，即遍历内部结构逐行输出与显示每个子句，与输入算例对比可人工判断解析功能的正确性。数据结构的设计可参考文献[1-3]。(15%)

⑶ DPLL过程：基于DPLL算法框架，实现SAT算例的求解。(35%)

⑷ 时间性能的测量：基于相应的时间处理函数（参考time.h），记录DPLL过程执行时间（以毫秒为单位），并作为输出信息的一部分。(5%)

⑸ 程序优化：对基本DPLL的实现进行存储结构、分支变元选取策略[1-3]等某一方面进行优化设计与实现，提供明确的性能优化率结果。优化率的计算公式为：[(t-to)/t]*100%,其中t 为未对DPLL优化时求解基准算例的执行时间，to则为优化DPLL实现时求解同一算例的执行时间。(15%)

功能（1）至（5）为基础功能，占功能分值的85%。

⑹ SAT应用：将数独游戏[5]问题转化为SAT问题[6-8]，并集成到上面的求解器进行问题求解，游戏可玩，具有一定的/简单的交互性。应用问题归约为SAT问题的具体方法可参考文献[3]与[6-8]。（15%）

2.4 实现与测试说明

数独游戏格局生成

数独游戏要求在9×9的网格中每个单元（cell）填入1至9的一个数字，必须满足：每一行、每一列及9个3×3的盒子中的数字都不重复。

一个数独游戏初始时已经提供了一些提示数，如图2.3，要求在剩下的空格中填满数字。初始游戏格局要求只有唯一解（一般至少要有17个提示数），基于推理可以求解。如何生成一个有效的数独游戏格局？一种方案可以从互联网（http://www.puzl.be/en/puzl_list.html）读取不少于50个不同的初始合法格局（此生成设计计分评定为良）；另一种方案是设计一种算法自动生成（此生成设计计分评定为优），一般可采用从完整合法填充开始，基于挖洞法生成[9]。

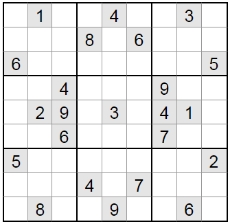
图2.3一个Sudoku格局

程序主控流程

根据设计问题的功能要求，图2.4提供了一个程序处理流程图，红色部分为程序中实现基于DPLL的SAT求解相关功能模块，蓝色部分是数独游戏生成、转化、求解等处理模块。此流程图仅供参考，不限定同学们的设计，可以以此为参照自由发挥。

图2.4参考程序流程图

程序模块化

设计程序要求模块化，程序源代码进行模块化组织。主要模块包括如下：

主控、交互与显示模块（display）

CNF解析模块（cnfparser）

核心DPLL模块( solver)

数独模块,包括数独生成、归约、求解(Sudoku)

CNF公式的内部存储结构

本应用处理的主要数据对象有变元或文字、子句、公式等。同学们可以分析这些数据的逻辑关系及其施加的基本运算而建立相应的抽象数据类型，设计其物理存储结构。如子句有创建createClause、销毁destroyClause、增加addClause、删除removeClause、判断是否为单子句isUnitClause、评估子句的真假状态evaluateClause等运算。由于每个CNF公式变元数与子句数可能不同，同一个实例中子句长度也可能不等,一种基本的处理方式是子句表示为由文字构成的链表；而整个公式又是由子句构成的链表，如图2.5所示，这里仅供参考（也许并非最优结构），同学们可自行设计相应的物理存储结构并进行优化。

图2.5 参考cnf公式存储结构图

测试算例要求(建议在内存≥8G的计算机上执行测试)

不少于30个SAT算例，其中可满足的算例不少于25个，不满足的算例不少于5个，大中小算例各占三分之一。鉴于大家实现的可能只是初级求解器，对算例规模的要求为：小型算例变元数为100个左右；中型算例变元数介于200-500个； 大型算例变元数600个以上。本设计提供部分cnf算例集,同学们可寻找与选择、扩充测试算例。在设计报告的测试分析部分列表给出每个测试算例下列信息：算例名、算例变元数、子句数与变元数比值、满足还是不满足或不确定、DPLL求解时间(t与to)以及优化率等信息。课堂检查时，主要对基准算例进行测试。

输出文件规范

对每个算例的求解结果要求输出到一个与算例同名的文件（文件扩展名为.res），文件内容与格式要求如下：

s 求解结果//1表示满足，0表示不满足，-1未定

v -1 2 -3 … //满足时，每个变元的赋值序列，-1表示第一个变元1取假，2表示第二个变元取真，用空格分开，此处为示例。

t 17     //以毫秒为单位的DPLL执行时间，可增加分支规则执行次数信息

2.5参考文献

[1] 张健著. 逻辑公式的可满足性判定—方法、工具及应用. 科学出版社，2000

[2]Tanbir Ahmed. An Implementation of the DPLL Algorithm. Masterthesis, Concordia University,Canada,2009

[3] 陈稳. 基于DPLL的SAT算法的研究与应用.硕士学位论文，电子科技大学，2011

[4]Carsten Sinz.Visualizing SAT Instances and Runs of the DPLL Algorithm.J Autom Reasoning (2007) 39:219–243

[5]360百科：数独游戏https://baike.so.com/doc/3390505-3569059.html

[6] Tjark Weber. A sat-based sudoku solver. In 12th International Conference on Logic for Programming, Artificial Intelligence and Reasoning, LPAR 2005, pages 11–15, 2005.

[7]Ins Lynce and Jol Ouaknine. Sudoku as a sat problem. In Proceedings of the 9th International Symposium on Artificial Intelligence and Mathematics, AIMATH 2006, Fort Lauderdale. Springer,2006.

[8] Uwe Pfeiffer, Tomas Karnagel and Guido Scheffler. A Sudoku-Solver for Large Puzzles using SAT. LPAR-17-short (EPiC Series, vol. 13), 52–57

[9] Sudoku Puzzles Generating: from Easy to Evil.

http://zhangroup.aporc.org/images/files/Paper_3485.pdf

[10] Robert Ganian and Stefan Szeider. Community Structure Inspired Algorithms for SAT and #SAT. SAT 2015,223-237360