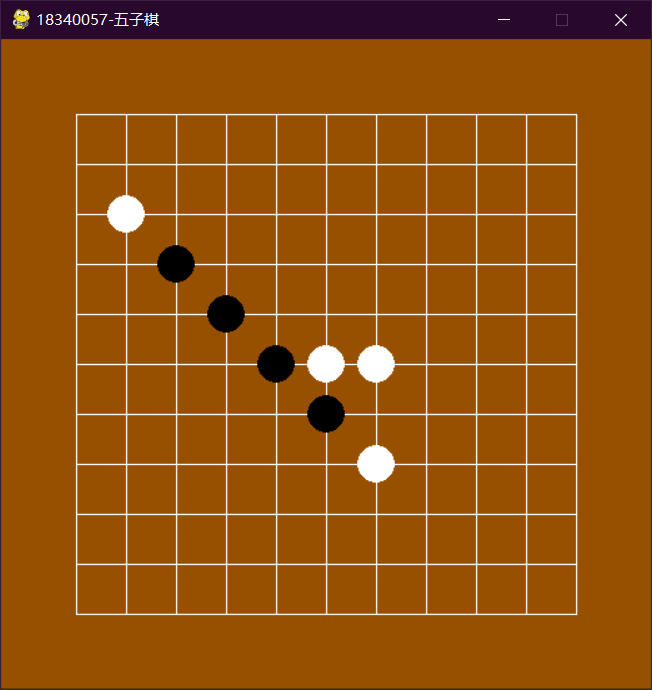
人工智能实验博弈树搜索

博弈树搜索

目录

人工智能实验博弈树搜索

博弈树搜索

1. 算法原理

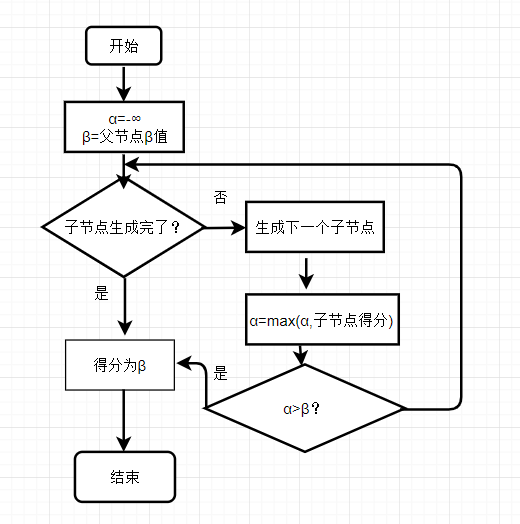
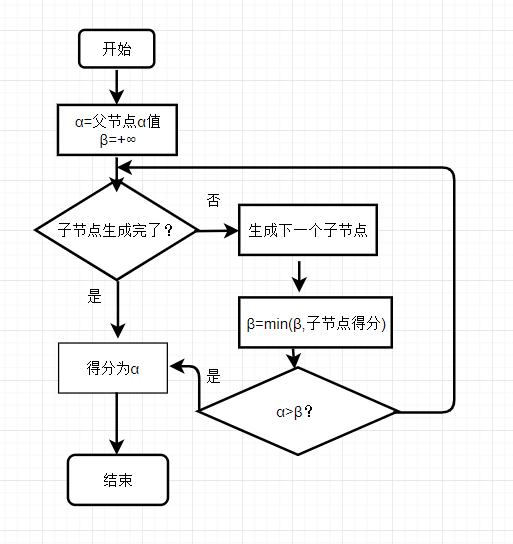
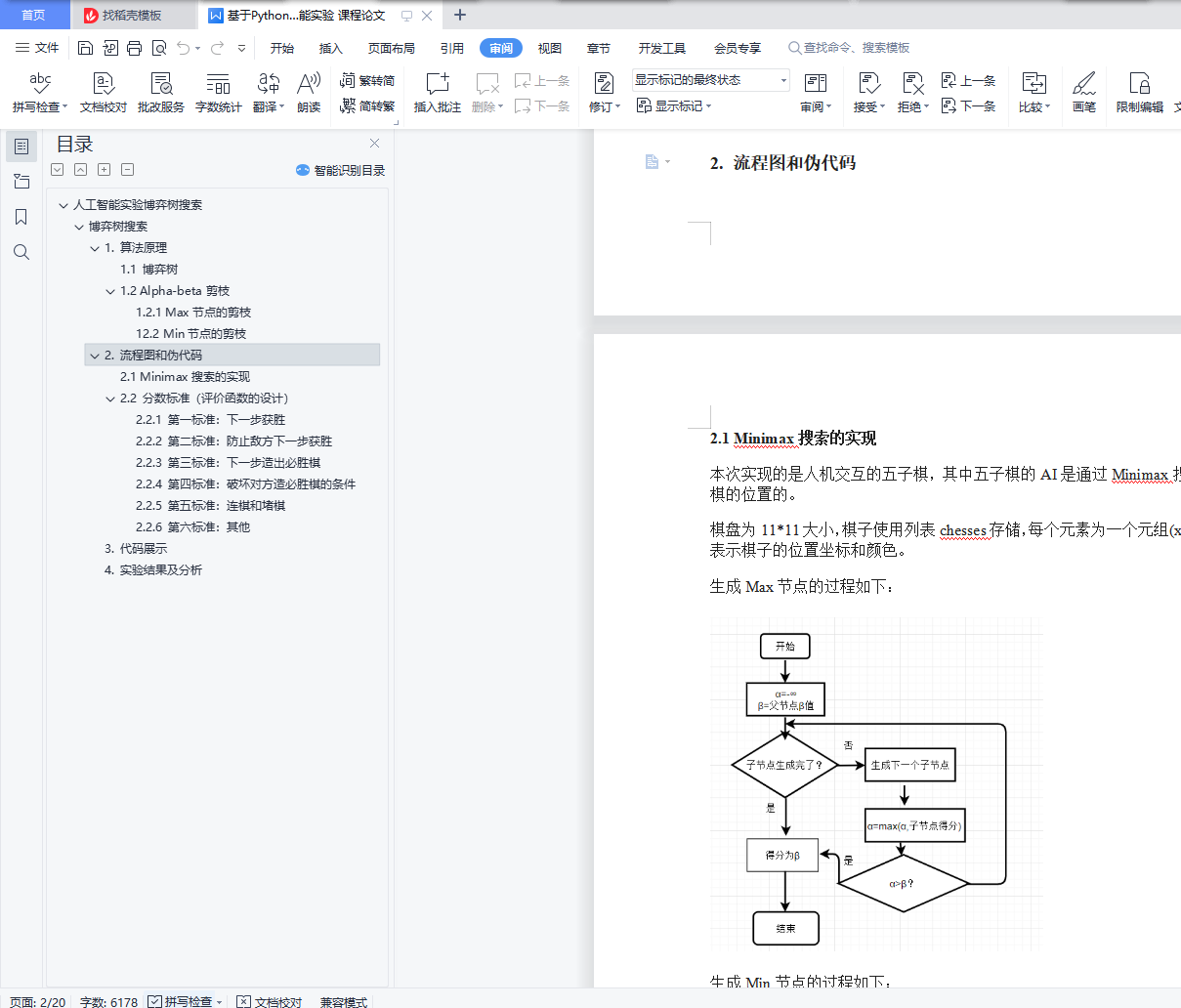
2. 流程图和伪代码

3. 代码展示

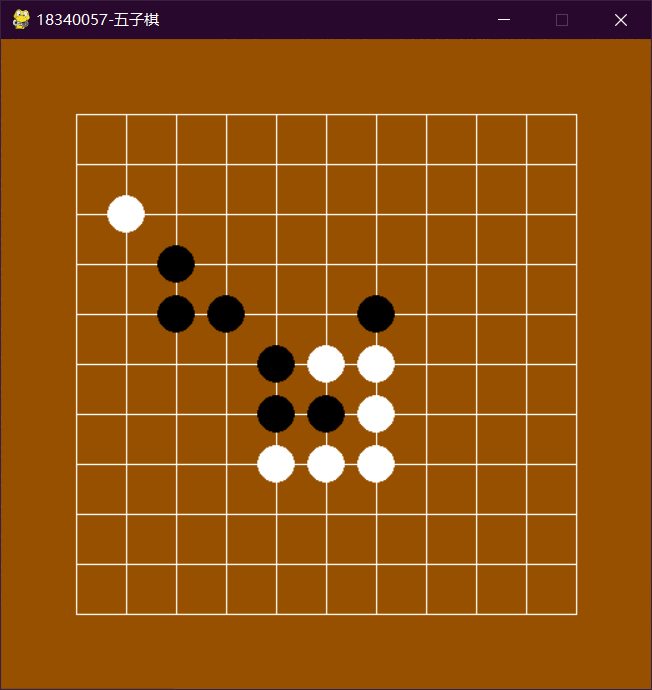
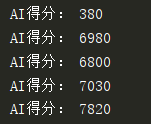
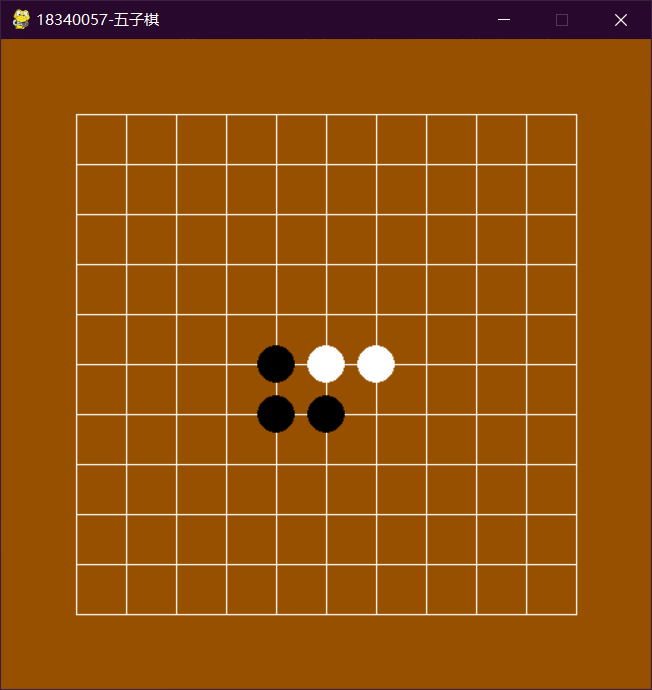
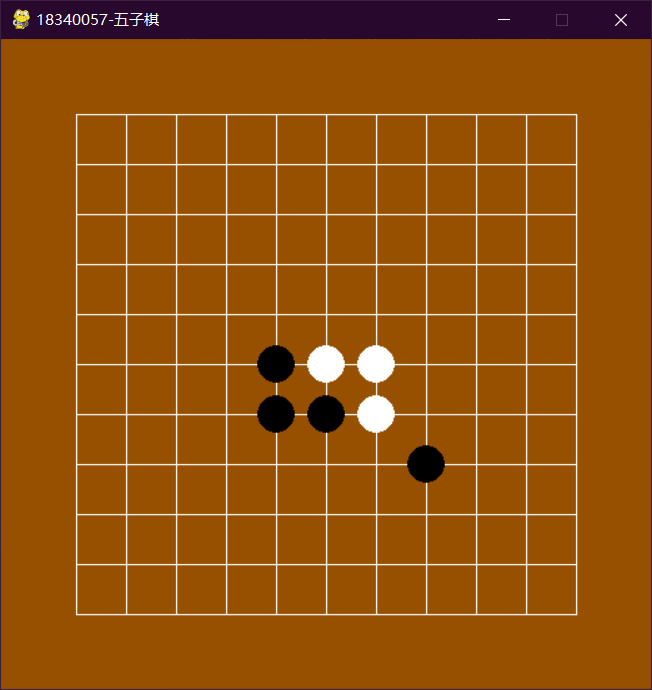
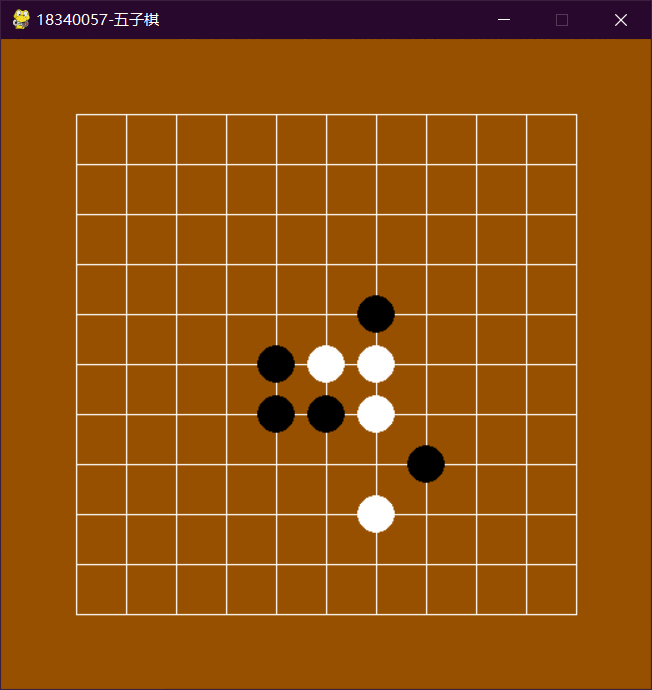
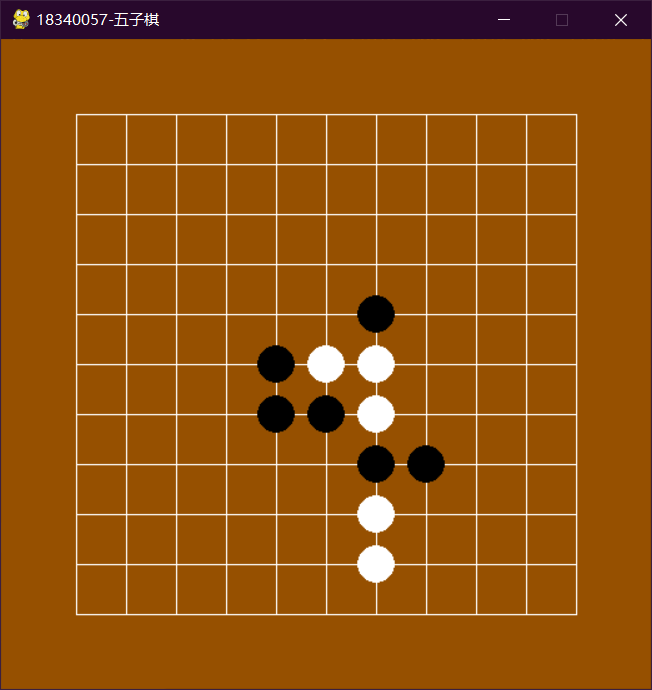
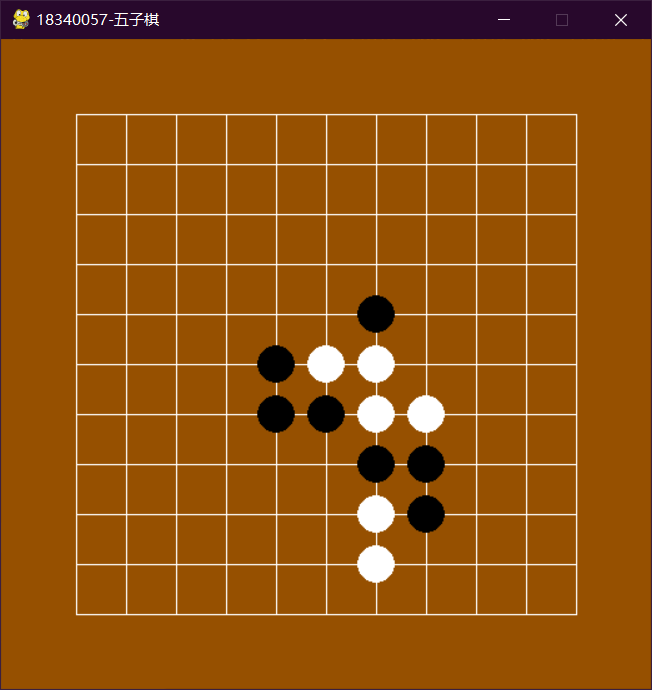
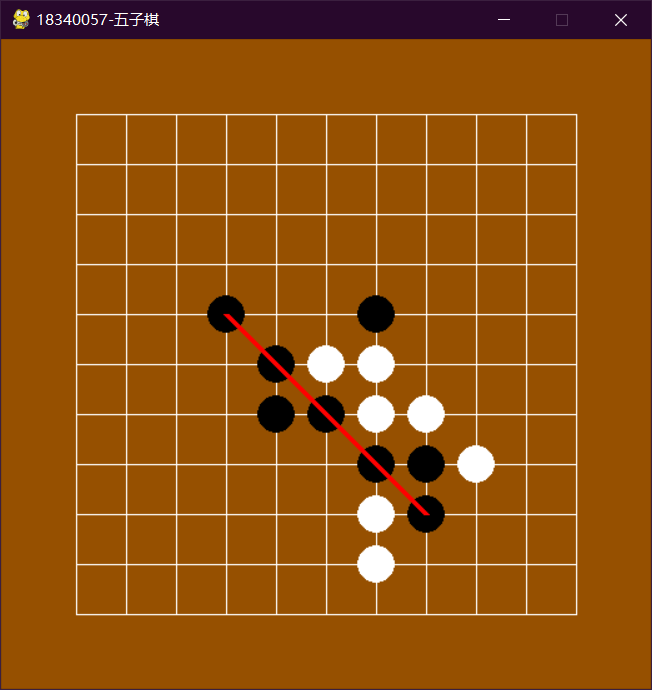
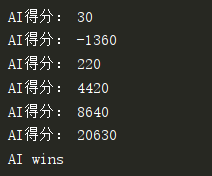
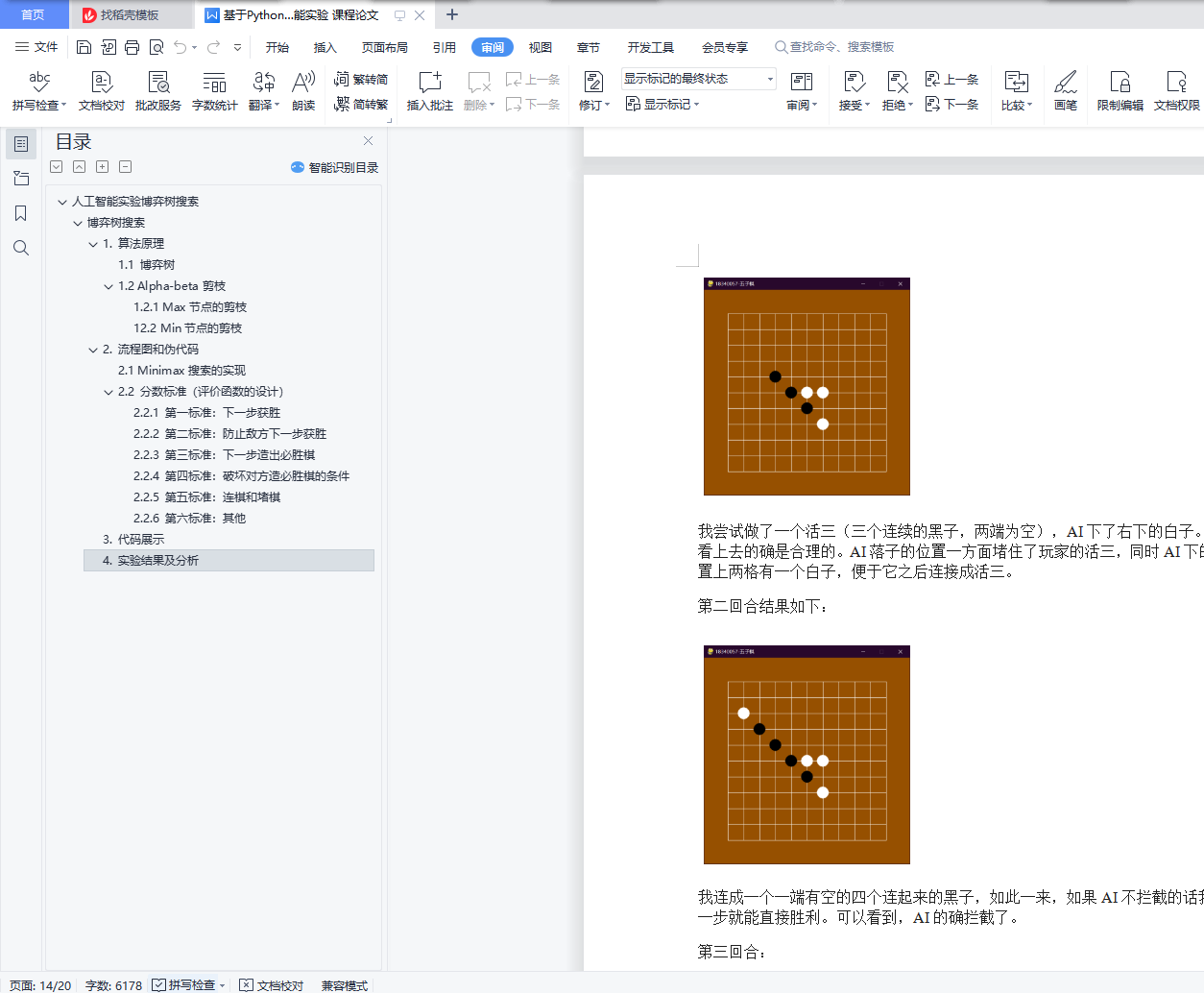
4. 实验结果及分析

1. 算法原理

1.1 博弈树

博弈树针对的是二人零和博弈的问题，二人轮流行动，行动时令自己的优势最大。二人零和博弈有如下特点：

· 确定性：二人的行动有多种选择，但最终的行动是确定的

· 信息完备性：博弈双方知道当前局势（即空间状态）的全部信息

· 零和性：一方的损失等于另一方的收益，二者得分相加恒为零

由以上特点，我们可以构造博弈树。因为信息完备性和确定性，可以用博弈树的每个节点表示一个确定的状态，在动作后得到的新状态作为子节点。对于每个状态都有同一个评价函数来评估双方的得分。因为零和性，一方通过决策使得自身的评价函数尽可能的大，另一方让队手的评价函数尽可能的小。因为二者是轮流行动的，在树的每一层让一方的评价函数取最大和最小交替进行。

由上述的特性，博弈树的搜索过程又被称为minimax搜索。博弈双方行动逐层交替，将评价函数值看做一方的分数，在那一方行动时要让分数尽可能的大，这样的节点被称为Max节点；在另一方行动时要让分数尽可能的小，这样的节点被称为Min节点。

要让一方的下一步采取最优的策略，需要进行树的搜索。在实际问题中，树往往非常大，因此只考虑一定的深度，而不是整个遍历。进行深入搜索时，轮流考虑Max节点和Min节点，每次都采取最优策略，最终得到本步的最优策略。