a) 选择合适的数据结构生成建立R-MAT图，计算图建立的时间（图数据规模Scale < 23, Edge-factor = 16）；

b) 选择合适的编程语言（OpenCL、Verilog等）在FPGA上实现BFS算法，在给定不同根节点的情况下计算每个点的深度，计算平均所达到的TEPS指标；

c) 对前面产生的结果进行验证和分析。

参考文献

[1]. 林子雨. 大数据技术原理与应用[M]. 人民邮电出版社, 2015.

[2]. Malewicz G, Austern M H, Bik A J C, et al. Pregel: a system for large-scale graph processing[C]. Proceedings of the 2010 ACM SIGMOD International Conference on Management of data. 2010: 135-146.

[3]. Salihoglu S, Widom J. GPS: a graph processing system. Proceedings of the 25th International Conference on Scientific and Statistical Database Management. 2013: 1–22.

[4]. Kyrola A, Blelloch G E, Guestrin C. Graphchi: Large-scale graph computation on just a pc. Proceedings of the10th USENIX Symposium on Operating Systems Design and Implementation, 2012: 31–46.

[5]. Gonzalez J E, Low Y, Gu H, et al. Powergraph: distributed graph-parallel computation on natural graphs. Proceedings of the 10th USENIX Symposium on Operating Systems Design and Implementation. 2012: 17–30.

[6]. Roy A, Mihailovic I, Zwaenepoel W. X-stream: Edge-centric graph processing using streaming partitions. Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles. 2013: 472-488.

[7]. Salihoglu S, Widom J. Optimizing graph algorithms on pregel-like systems. Proceedings of the VLDB Endowment, 2014, 7(7): 577-588.

[8]. The Laboratory for Web Algorithmics, http://law.di.unimi.it/datasets.php.

[9]. Tian Y, Balmin A, Corsten S A, et al. From think like a vertex to think like a graph. Proceedings of the VLDB Endowment, 2013, 7(3): 193-204.

[10]. Yan D, Cheng J, Lu Y, et al. Blogel: A block-centric framework for distributed computation on real-world graphs. Proceedings of the VLDB Endowment, 2014, 7(14): 1981-1992.

[11]. The Center for Discrete Mathematics and Theoret- ical Computer Science, http://www.dis.uniroma1.it/challenge9/download.shtml.

[12]. Simmhan Y, Kumbhare A, Wickramaarachchi C, et al. Goffish: A sub-graph centric framework for large-scale graph analytics. Proceedings of the 2014 European Conference on Parallel Processing. 2014: 451-462.

[13]. Xie W, Wang G, Bindel D, et al. Fast iterative graph computation with block updates. Proceedings of the VLDB Endowment, 2013, 6(14): 2014-2025.

[14]. J. Shun, G. E. Blelloch. Ligra: a lightweight graph processing framework for shared memory. Proceedings of the 2013 ACM SIGPLAN Symp. Principles and Practice of Parallel Programming, 2013: 135–146.

[15]. Nguyen D, Lenharth A, Pingali K. A lightweight infrastructure for graph analytics. Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles. 2013:456-471.

[16]. YUAN, P., ZHANG, W., XIE, C., et al. Fast iterative graph computation: a path centric approach. Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, 2014:401–412.

[17]. Zhu X, Han W, Chen W. GridGraph: large-scale graph processing on a single machine using 2-level hierarchical partitioning. Proceedings of the Usenix Conference on Annual Technical Conference. 2015:375-386.

[18]. LOW, Y., BICKSON, D., GONZALEZ, J., et al Distributed graphlab: a framework for machine learning and data mining in the cloud. Proceedings of the VLDB Endowment, 2012, 5(8):716–727.

[19]. Beamer S, Asanovic K, Patterson D. Direction-optimizing Breadth-First Search. Proceedings of the International Conference for High PERFORMANCE Computing, Networking, Storage and Analysis. 2012:1-10.

[20]. Liu H, Huang H H. Enterprise: breadth-first graph traversal on GPUs. Proceedings of the International Conference for High PERFORMANCE Computing, Networking, Storage and Analysis. 2015:1-12.

[21]. Pascal Architecture Whitepaper – Nvidia. https://images.nvidia.com/content/pdf/tesla/whitepaper/pascal-architecture-whitepaper.pdf

[22]. Merrill D, Garland M, Grimshaw A. Scalable GPU graph traversal. Acm Sigplan Notices, 2012, 47(8):117-128.

[23]. Wang, Yangzihao, et al. "Gunrock: A high-performance graph processing library on the GPU." Proceedings of the 21st ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. 2015: 265-266.

[24]. Han W, Mawhirter D, Wu B, et al. Graphie: Large-Scale Asynchronous Graph Traversals on Just a GPU. Proceedings of the International Conference on Parallel Architectures and Compilation Techniques. 2017:233-245.

[25]. Jeffers, James, James Reinders, Avinash Sodani. Intel Xeon Phi Processor High Performance Programming: Knights Landing Edition. Morgan Kaufmann, 2016.

[26]. Maass S, Min C, Kashyap S, et al. Mosaic: Processing a Trillion-Edge Graph on a Single Machine. Proceedings of the Twelfth European Conference on Computer Systems. 2017:527-543.

[27]. S. Beamer, K. Asanovic, D. Patterson, “Locality Exists in Graph Processing: Workload Characterization on an Ivy Bridge Server,” Proceedings of IEEE International Symposium on Workload Characterization, 2015:56-65

[28]. L. Nai, Y. Xia, I. G. Tanase, et al, “GraphBig: Understanding Graph Computing in the Context of Industrial Solutions,” Proceedings of IEEE International Conference for High Performance Computing, Networking, Storage and Analysis, 2015:1-12.

[29]. G. Dai, T. Huang, Y. Chi, et al. “ForeGraph: Exploring Large-Scale Graph Processing on Multi-FPGA Architecture,” Proceedings of ACM International Symposium on Field-Programmable Gate Arrays, 2017:217-226

[30]. S. Zhou, C. Chelmis, V. K. Prasanna, “High-Throughput and Energy-Efficient Graph Processing on FPGA,” Proceedings of IEEE International Symposium on Field-Programmable Custom Computing Machines, 2016:103-110.

[31]. G.Dai, Y. Chi, Y. Wang, et al, “FPGP: Graph Processing Framework on FPGA: A Case Study of Breadth-First Search,” Proceedings of ACM International Symposium on Field-Programmable Gate Arrays, 2016: 105-110.

[32]. T. J. Ham, L. Wu, N. Sundaram, et al, “Graphicionado: A High-Performance and Energy-Efficient Accelerator for Graph Analytics,” Proceedings of IEEE International Symposium on Microarchitecture, 2016:1-13.

[33]. M. M. Ozdal, S. Yesil, T. Kim, et al, “Energy Efficient Architecture for Graph Analytics Accelerators,” Proceedings of ACM/IEEE Annual International Symposium on Computer Architecture, 2016:166-177.

[34]. N. Sundaram, N. Satish, M. M. A. Patwary, et al, “GraphMat: High Performance Graph Analytics Made Productive,” Proceedings of the VLDB Endowment, 2015, 8(11): 1214-1225.

[35]. https://en.wikipedia.org/wiki/PageRank

[36]. https://en.wikipedia.org/wiki/Bellman%E2%80%93Ford_algorithm

[37]. Ullmann J R. An algorithm for subgraph isomorphism[J]. Journal of the ACM, 1976, 23(1): 31-42.

[38]. Shang H, Zhang Y, Lin X, et al. Taming verification hardness: an efficient algorithm for testing subgraph isomorphism[J]. Proceedings of the VLDB Endowment, 2008, 1(1):364-375.

[39]. Zhao P, Han J. On graph query optimization in large networks[C]. Proceedings of the VLDB Endowment, 2010, 3(1):340-351.

[40]. He H, Singh A K. Graphs-at-a-time: query language and access methods for graph databases. Proceedings of the 2008 ACM SIGMOD international conference on Management of data. 2008: 405-418.

[41]. Agrawal R, Borgida A, Jagadish H V. Efficient management of transitive relationships in large data and knowledge bases. Acm Sigmod Record, 1989, 18(2):253-262.

[42]. Graph500 : http://www.graph500.org/

[43]. Chakrabarti D, Zhan Y, Faloutsos C, et al. R-MAT: A Recursive Model for Graph Mining. Proceedings of the siam international conference on data mining, 2004: 442-446.

[44]. SNAP : http://snap.stanford.edu/

[45]. The Game Trace Archive : http://gta.st.ewi.tudelft.nl/

[46]. Murphy R C, Wheeler K B, Barrett B W, et al. Introducing the graph 500. Cray Users Group, 2010, 19: 45-74.

[47]. 衡冬冬, 唐玉华, 易晓东,等. 并行原型系统上BFS算法设计实现与测试分析. 计算机工程与科学, 2017, 39(1):27-34.

索引

ASIC 42

BSP（Bulk Synchronous Parallel）5

编程模型   5

单机图计算 20

FPGA 40

GAS（Gather-Apply-Scatter）7

Graph500 53

高访存/计算比  4

局部性差  4

混合划分 16

MIC 38

Push消息交换模式 17

Push消息交换模式 17

PSW模型 26

SIMD 35

双滑动窗口 33

同步模式 18

图计算   2

图划分 14

拓扑属性算法 45

图数据结构  1-2

图数据驱动  4

图数据管理和查询算法 50

TLAV（Think Like a Vertex） 5

异步模式 19

以边为中心模型  8

以边为中心划分 15

以点为中心模型  5

以点为中心划分 15

以路径为中心模型 9

以子图为中心模型 13

6.7 图计算性能评价

随着大数据时代的到来，涌现出越来越多的数据分析应用，包括医疗大数据查询、生物信息基因测序、社交网络关系数据挖掘等。对于这些应用，图计算算法是它们的核心部分。图计算的算法与传统的规则程序相比，在计算和访存上千差万别，有着不同的性能特性和结构需求，所以传统的评测程序对这一类应用已经不具有代表性，亟需新的评测标准。

Graph500是由来自学术界、工业界和国家实验室的多位国际HPC专家共同为面向数据密集的大规模图分析应用提出的评测标准[42]。它在基于随机图生成器Kronecker生成的无向大图中执行广度优先搜索（Breadth-First Search, BFS）、单源最短路(Single Source Shortest Path, SSSP)算法来更加全面地对超级计算机系统性能进行评价。如图 6-7-1所示，Graph500基准测试程序（benchmark）主要包括图生成、图建立（Kernel 1）、图搜索（Kernel 2-BFS或Kernel 3-SSSP，该部分以BFS为例进行详细说明）、验证、结果输出[47]。

图 6-7-1  Graph500基准测试程序流程示意图

图生成：可扩展数据生成器将构建包含节点（vertex）标识符的边元组（edge tuples）列表。边元组具有<StartVertex, EndVertex, Weight>的形式，用于表示每一条无向边。其中StartVertex是一个节点标识，EndVertex是另一个节点标识，Weight是边的权重。节点标识空间是[0,N)（N是图中节点数量）的整数集合。权重空间是[0,1)的单精度浮点数集合。如果边元组用于运行BFS，则不需要生成边权重。图的规模是有由用户输入的参数SCALE、edgefactor确定的，其中SCALE表示图节点规模，edgefactor表示图的边数与其节点数之比，即图中节点的平均度数，事实上，Graph500 推荐edgefactor 设为16。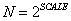 表示图节点个数，可以使用任意N个不同整数的集合来对节点进行编号，但是每个节点编号必须至少分配48个bit，必要情况下为边权重分配32个bit。 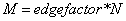表示图边数。图生成器是类似于递归矩阵（R-MAT）的图生成算法的Kronecker[43]。为了便于讨论，这个R-MAT生成器使用了一个邻接矩阵数据结构; 然而，具体实现可以使用任何替代方法来输出边元组的等价列表。该模型将图的邻接矩阵递归地细分为四个相等大小的分区，并以不等概率在这些分区内分布边。最初，邻接矩阵是空的，接着一次添加一个边，每个边分别以A，B，C和D的概率选择四个分区中的一个。这些概率也是固定的，A=0.57、B=0.19、C=0.19、D=1-(A+B+C)=0.05。边权重从[0,1)区间随机选取，均匀分布。图生成器可能在两个节点之间创建少量的多条边或在单节点上创建环。在随后的计算中，可以忽略多个边、环和孤立的节点，但必须将其包含在提供给图建立部分的边列表中。该算法还生成具有高度局部性的数据元组。因此，作为最后一步，必须随机置换节点数，然后随机调整边元组。图生成阶段允许并行运行数据生成器，在这种情况下，有必要确保节点全局命名，并且生成的数据不具有任何局部性。如表 6-7-1所示，根据Graph500基准测试程序输入参数的不同，可以将求解问题划分为六个不同的数据规模，分别为Toy、Mini、Small、Medium、Large、Huge[42]。表 6-7-2总结了Graph 500基准的建议数据集类别，代表了关键的商业和科学问题。广泛使用的数据集有SNAP[44]、The Game Trace Archive[45]。

表 6-7-1  Graph500的六种数据规模

图建立（kernel 1）：该部分将边元组转换为用于后续部分的任何表示图的数据结构（例如CSR （压缩稀疏行）或CSC（压缩稀疏列）），生成的数据结构不能被后续部分更改。用户只需要为该部分提供边表和边表的大小，更多的信息需要在该部分计算，如顶点的数量等。需要注意的是该过程的运行时间称为图建立时间，不计入性能计算。

表 6-7-2  Graph500建议的数据集类别[46]

图搜索（kernel 2–BFS或kernel 3-SSSP）：程序随机生成一个根节点，BFS从单个根节点开始，然后分阶段地发现和标记它的邻居，然后标记它的邻居的邻居等。Graph500指定BFS的输入和输出，并且对计算施加一些限制。然而，并不限制BFS算法本身的选择，只要它产生一个正确的BFS树作为输出。这部分运行时间计入性能计算，但是根节点产生的时间不计入性能计算。

验证：在每个根节点的图搜索完成之后，该部分会对搜索结果进行验证，该部分运行时间不计入性能计算。验证程序需要确保如下条件：

1. 图搜索阶段产生的结果BFS/SSSP树是树结构，不包含环。

2. BFS树上的每条边连接的两个节点的深度（每个节点的深度是该节点到根节点的距离）差为1；SSSP树上的每条边连接的两个节点的深度差至多为该边的权重。

3. 对于输入的边元组中每一条边的两个节点的深度差不大于1（针对BFS）或边权重（针对SSSP），或者这两个节点都不在树上。

4. 树上的任意两个节点都连通。

5. 树上的边为边元组中的边。

图搜索验证部分循环执行64次，每次随机生成一个非孤立节点作为根节点。

结果输出：包括基本参数图规模SCALE、节点平均度数edgefactor、根节点数目，以及一些统计结果，主要有BFS/SSSP图搜索时间、访问边数、每秒遍历边数（TEPS,traversed edges per second）。BFS/SSSP图搜索时间从访问根节点开始计时，当写入内存时终止计时，不计时任何I/O。Graph500衡量单个搜索的性能，但是为了计算均值，我们运行64次搜索，记录每一次搜索的时间。为了比较各种体系结构，编程模型和框架中graph500“图搜索”实现的性能，我们定义了新的性能指标，称为每秒遍历边数（TEPS）：，其中为生成图的边数，为图搜索部分的时间。Graph500最终将产生五个TEPS指标，分别为最小值、四分之一位数、调和平均值、四分之三位数和最大值。

针对一个图计算系统的评价指标主要包括图计算BFS性能指标、BFS性能功耗比指标、每轮迭代所需时间、可扩展性。例如，评价一个基于FPGA的图计算系统好坏，可以从两个指标分析。第一BFS性能指标，现有的FPGA方案性能约为0.3GTEPS（参考ForeGraph，按照Graph500标准测试方案，采用SCALE不大于22的图数据集运行BFS标准代码，进行实际性能测试）；第二BFS性能功耗比指标，经典的CPU与GPU系统性能功耗比约为0.002GTEPS/W（参考GraphChi与Medusa）；某个基于FPGA的图计算系统的BFS性能指标比0.3GTEPS越大，性能功耗比指标比0.002GTEPS/W越大，说明该系统越好。

表 6-7-3  Graph500 2017年11月公布的BFS排名

表 6-7-4  Graph500 2017年11月公布的SSSP排名

在2010年国际超级计算大会（Supercomputing Conference, SC10）首次发布Graph500排行榜，用于测量超级计算机在复杂图问题应用方面的吞吐能力，以补充传统的TOP500和Green500。最新的Graph500（2017年11月公布）排名中已经包括235台机器，可见业界对Graph500的重视程度。表 6-7-3、表 6-7-4列出了最新Graph500的前十名机器。

6.8 本章小结

图计算是大数据时代的关键分析手段之一。它能够挖掘事物之间潜在不易洞察的联系。图计算应用和相关系统的研究在近年来一直处于火热状态。本章首先介绍了图计算的应用需求，列举了图计算几个常见的应用场景，并分析了图计算的特点，比如数据访问非规则性、高访存/计算比等特点。图计算的天然特性给图计算系统的设计带来了诸多挑战。本章随后介绍了图计算系统设计中常见的技术手段，包括并行编程模型，图划分和通信策略等。接着，本章列举了典型图计算系统示例。除此之外还介绍了近年来研究火热的图计算加速技术，利用新兴的物理器件来实现高效的图计算。最后，本章介绍了常用的图算法以及图计算性能评测标准Graph500[42]。本章全面系统的介绍了图计算的特征和前沿的研究成果，给未来图计算领域研究给出一定参考和指导。

6.9习题

名词解释

1. 解释以下名词

图结构、图计算、图划分、图查询、核外图计算、内存图计算、GTEPS

基础性算法设计题

2. 采用Scatter-Gather编程模型，写出广度优先搜索算法BFS、网页排名算法PageRank、单源点最短连接算法SSSP和强连通算法SCC伪代码。

进阶性算法设计题

3. 最经典的大规模图划分算法是散列划分，即每个顶点首先赋予唯一的ID号，将图的顶点散列划分到p个分区中，那么

a) 每条边被切割的数学期望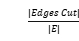是多少？因切割而产生的复制点，数学期望是多少个？

b) 对于指数为α的幂律图，因切割而产生的复制点，数学期望是多少个？

c) 散列划分的优势和缺陷是什么？

4. 对于幂律图中的高维度节点（例如Twitter中具有大量粉丝的美国总统），有以下几种处理方式：

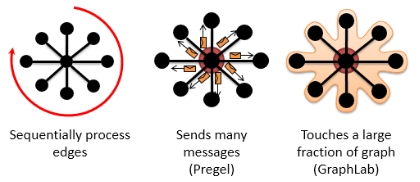
顺序处理            发送消息          接触大部分图

共享状态：异步执行                共享状态：同步执行

请写出以上几种方法的缺陷。

观察多层划分算法的伪代码，尝试理解操作Coarsening和Uncoarsening的意义

Multilevel Graph Partition (Graph G)

①  Take the weighted undirected graph as input

②  While (|V|> coarsening threshold) perform

Coarsening (Gi to Gi +1 )

③  For all v in V

If vertex degree (v) is high perform

Balanced partitioning

Else

Perform Greedy partitioning

④  Simulated annealing(initial partition)

⑤  While (Gi!= G) perform

Uncoarsening (Gi to Gi-1 )

5. 下图是随机最小割的基本原理：点的收缩，请尝试使用伪代码写出该算法。

应用实践思考题

  全套毕业设计论文现成成品资料请咨询微信号：biyezuopin QQ：2922748026     返回首页 如转载请注明来源于www.biyezuopin.vip