6.4 单机图计算系统

单机图计算系统能充分发挥单台机器处理图计算任务的能力，避免分布式系统下代价高昂的网络通信开销，但是此类系统受限于固定的硬件资源，无法实现很好的扩展性，处理的时间通常和图数据大小成比例。单机图计算系统可以分为两类，面向高端多核、大内存服务器的内存（In-memory）图计算系统，以及面向商用PC的核外（Out-of-core）图计算系统。前者在处理过程中将图数据完全放入内存中，后者通常利用磁盘存放图数据，采取一定的划分策略分块处理。

一个典型的单机图计算系统通常会将点和边划分为小的分片，从而使得分片能够在高速的存储设备中进行处理，提供充分的并行性和优化的访存模式。对于内存图计算系统，图数据划分的目的是使得每个核心能够有效的处理各自的分片，有些内存图计算系统不需要显式的划分策略，只需在计算过程中对任务进行适应性的调度来取得很好的并行效果。对于核外系统，图数据无法被全部加载进内存，图划分使得分片能够被加载进内存进行处理，对于以点为中心的系统，一般将点和边的分片同时加载进内存中，以边为中心的系统只将点分片整个加载进内存，边数据从磁盘上以流的形式加载处理。

下面按照两个类别，分别介绍六个典型的单机图计算系统，它们在编程模型、执行模型、任务调度和图划分策略等方面采取了相应的优化手段。概括来讲有基于push/pull切换的编程模型，以点为中心、以边为中心和以路径为中心的执行模式，自主调度策略，基于路径和网格的划分策略等。

6.4.1 内存图计算系统

一、Ligra系统

Ligra[14]在PPoPP’13上被提出，是一个基于共享内存的轻量级单机图计算系统。Ligra是受到Beamer工作[19]的启发，其核心思想是根据执行过程中活跃点子集的大小、出度等情况，自动在push和pull计算模式之间切换，加快图计算特别是图遍历算法的收敛。

Ligra适用于共享内存的设备，现有的单个商用服务器已经能够容易的在内存中处理百亿条边级别的图数据，相比于分布式集群，单服务器上能够实现更优的单核性能，并且可靠性更高。大多数图算法例如BFS（Breadth First Search）、PageRank、SSSP等在处理的过程中存在多轮迭代，并且每次只处理所有点的一个子集，于是可以根据这个子集的特征选择合适的方式来执行。Ligra为此提供了一个基于边映射函数edgeMap、点映射函数vertexMap和点子集类型vertexSubset的编程抽象，在整个计算过程中，图的所有数据全部被加载到内存中。

Push模式和pull模式。在push模式中，子集中的点以一种稀疏的方式表示，即点的ID数组，大小为子集大小，根据点的度数以并行或者串行的方式循环处理子集中每个点的出边执行定义的操作；在Pull模式中，整个图的所有点以一个比特数组的方式表示，数组大小为原始点集大小，子集中的点对应的位置设为1，其他位置为0，对原始点集中所有点，如果其源点在子集中，则执行定义的操作。

Ligra的编程接口。前面提到，Ligra定义了一个点的子集类型vertexSubset，存放活跃点集，每轮迭代只对这个子集进行处理，根据计算会生成新的子集，中间生成的不同vertexSubset可以被保留以便重复使用。vertexMap函数对输入子集中的所有点执行用户定义的函数，返回一个新的子集；edgeMap函数根据输入子集大小和点的出度启发式的选择执行edgeMapSparse函数还是edgeMapDense函数，两个函数的详细过程如图 6-4-1所示，edgeMapSparse函数按照push模式执行，并行处理子集中的每个点，使用F(u, ngh)作用于点的所有出边，这个过程也是并行的，函数最后返回一个稀疏形式表示的新子集，复杂度相当于对子集中的点计算其出度之和；edgeMapDense函数按照pull模式执行，并行处理原始点集中的所有点，对源点在活跃点集中的边顺序的使用F(ngh, v)函数，直到C(u)返回负值，最终返回一个密集形式表示的新子集。

图 6-4-1  edgeMap中push和pull模式调用的函数执行过程[14]

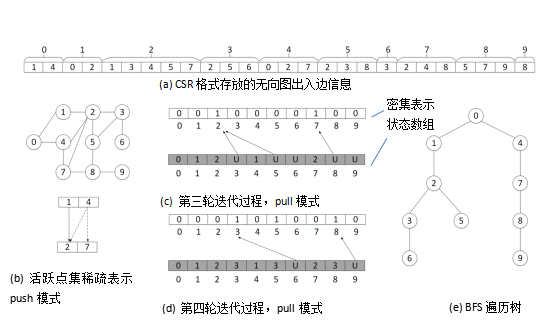
图 6-4-2  push和pull模式切换的BFS算法执行过程[20]

下面给出一个BFS的执行过程，详见图 6-4-2。0号点为根节点处在第0层，计算每个点所处层数，其中状态数组存放每个点的层数，U表示还没被访问到。b图中当前活跃点集是{1, 4}，该点集以稀疏形式存放，查找它们的出边节点2和7，赋予当前层数，生成新的活跃点集{2, 7}，进入下一轮迭代；c图是以密集形式存放的活跃点集，用[0,0,1,0,0,0,0,1,0,0]表示，对所有点中还没有被访问过的点找相应的源点如果在活跃集中则赋予当前层数。

Ligra在图数据表示方面同时采用CSR（Compressed Sparse Row）和CSC（Compressed Sparse Column）两种形式来分别存放点的出边信息和入边信息，在push模式下需要用到出边信息，在pull模式下需要入边信息，在执行过程中这两个边表都要求加载进内存。

总的来看Ligra特别适合处理图遍历算法，通过在运行过程中自动切换push和pull模式加快算法的收敛，对于power-law图和小直径的图加速效果最明显。但是Ligra缺乏调度策略的支持，这在处理某些算法时性能上会大打折扣。

二、Galois系统

Galois单机图计算系统[15]在SOSP’13上被提出，基于一个现有的系统Galois扩展设计。Galois图计算系统的核心思想是在数据驱动（data-driven）的计算模式下，充分发挥自主调度（autonomous scheduling）的优势。为此Galois设计了一个机器拓扑感知的任务调度器和优先级任务调度器，并提供了相应的扩展库和运行时系统，同时支持多种编程接口。

Galois指出现有的几个以点为中心计算的模型通常采用协调调度策略，在每一轮迭代设置同步保证操作的正确性，在处理多数具有一般性的高性能图分析任务时效率不高，而受数据驱动的自主调度（autonomous scheduling）通常能够实现更好的性能。Galois总结了图计算执行过程的几个特点：（1）作用于活跃点的operator功能函数在功能上可以修改图的属性值或者图的结构，在执行方式下有push和pull两种；（2）operator作用范围的设置有两种策略，一种是基于拓扑结构固定设置好，一种是根据计算过程中数据驱动动态的生成相应的活跃点集，前者在实现上简单，后者实现上更有挑战，但是更加高效；（3）在任务调度策略上，当任务多于处理器线程的时候，可以采用自主调度策略或者协调调度策略，前者根据任务优先级异步执行任务，保证并行任务可串行化即可，后者需要线程在执行分配的任务后等待每一轮的同步然后继续执行。通常数据驱动的执行模式和自主调度策略下的执行速度比其他方式更快，然而它们需要有相应的任务优先级设置和细粒度调度来支持负载均衡充分发挥并行性。常见的几个图计算系统不完全支持上述特性，Galois为此设计了一个机器拓扑感知的任务调度器和优先级任务调度器，并提供了一个扩展库和运行时系统，能够支持上述所列图计算特性。

机器拓扑感知的任务调度（Machine-topology-aware Scheduling）。这是Galois调度器的核心所在，当没有设置优先级的时候，Galois使用一个并发包（concurrent bag）来装载任务（活跃点集），包里面的任务是无序可并行执行的，可以插入新的任务或请求内部的任务。详细的过程如图 6-4-3(a)所示，机器的每个计算核心拥有一个称为chunk的数据结构，这是一个可以容纳8-64个任务的环状缓冲区。计算核心通过chunk插入新任务或者获取任务工作。Bag中有多个package，每个package关联一堆chunk，当计算核心的chunk为满状态就会到package这一层插入任务到其他chunk，当计算核心的chunk为空就会到package这一层寻找其他chunk中的任务，如果package也为空就去另一个package查询。

图 6-4-3  Galois调度机制数据结构[15]

优先级调度。在任务具有优先级的情况下，Galois结合前面的机器拓扑感知任务调度策略，设计一个称为obim的调度器，obim中包含多个并发包，每个包中放置同等优先级的任务，同等优先级的任务可以并发执行，同时优先级靠前的任务先执行。如图 6-4-3 (b)所示，obim的全局映射包含三个包，分别存放了任务1、3、7，全局维护一个操作日志记录全局包的活动；每个线程维护一个本地包映射，缓存全局的包结构，同时记录日志点，当线程需要插入和获取任务的时候在本地对相应优先级的包进行操作，如果本地无法找到特定优先级的包，根据全局日志记录，将全局最新结构拷贝，如果仍然没有找到特定优先级的包，则创建一个新优先级的包，同步全局和本地包和日志。所有线程会共享当前处理任务的优先级，提高任务获取效率，保证任务的执行顺序。

Galois还提供了一套扩展库和运行时系统来支持其任务调度策略，包括内存分配机制、拓扑感知的同步机制和代码优化机制。用户能够通过Galois灵活丰富的编程接口尽可能简单的实现复杂的功能。Galois作为一个一般性的图计算编程框架除了自身提供的基于任务调度策略的执行模式之外，还可以支持其他图计算系统的API，例如GraphLab[18]的点程序执行模式，PowerGraph[5]的GAS执行模式，GraphChi[4]部分利用外存计算的手段，Ligra[14]的push和pull切换策略，以及将核外计算和push/pull结合执行的模式。

总的来看，Galois利用更加一般性的编程框架处理图算法，相比于其他系统取得了更好的性能，其任务调度机制在处理大直径的图数据时可获得数量级的性能提升，并且基于Galois的其他图计算系统的API实现能比原生系统获得更好的性能。

6.4.2 核外图计算系统

一、GraphChi系统

GraphChi [4] 是Kyrola等人在OSDI’12上提出来的一个以点为中心的单机图计算系统。该系统提出了并行滑动窗口（Parallel Sliding Windows, PSW）技术优化图计算过程中对磁盘的访问，同时使用了空间高效的图数据结构和划分策略，并且它具有动态选择性调度模块，能在更新或图结构发生改变的时候能够将按需求将某些点进行调度从而进一步提高性能。

利用分布式图计算系统处理大规模图计算任务，需要对图进行划分以最小化节点之间的通信开销，同时也要保证负载均衡，这是很困难的事情，此外维护一个大集群的正常运行也会面临各种无法预测的故障。从编程者的角度看，在分布式系统上进行测试调优也很困难。研究在单机上高效处理同等规模的图计算任务时，一个方案是使用具有大内存的高端服务器进行处理，然而价格十分昂贵，另一个方案是基于外存的图计算系统。GraphChi是第一个基于磁盘的图计算系统，设计该系统面临的最主要问题是计算过程中对磁盘的随机访问行为，GraphChi的解决方案是将边数据进行预处理，按照特定的格式存放，用并行滑动窗口的方式减少对磁盘的随机访问次数。

图划分策略。GraphChi在图的预处理过程中将边划分为多个shard，将整个点集分为不相交的interval，其中每个interval对应一个shard，shard中存放对应interval 中所有点的入边信息，shard中的边按照源点的顺序排序并以压缩邻接矩阵的格式存放在磁盘上，最终使得每个shard能够被完全的加载进内存，如图 6-4-4所示。这样的设计基于以点为中心的计算特征，通过读边的信息获取邻居节点的数据，计算后将新的值赋给当前顶点，同时把新的数据更新到边上分发给邻居节点。这样的划分保证在每次处理一个interval中的点的时候点的入边和出边的信息能够同时被完全的加载进内存，每个interval中点的入边在磁盘上是连续存放的，按照源点的排序使得访问多个shard中相应出边信息也是顺序的。不过这种划分在预处理的时候有较大时间开销。

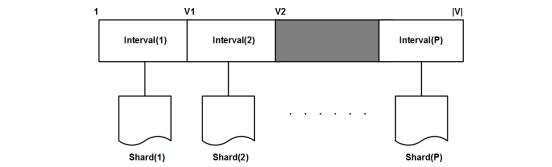
图 6-4-4  GraphChi的点集和边集划分示意图[4]

并行滑动窗口。GraphChi使用了一个新颖的计算模型称为并行滑动窗口（PSW），PSW是一个异步计算模型，能够从磁盘处理边数据，只涉及到很少的随机访存。PSW分三个阶段处理一个图：从磁盘加载图的一个子集，然后对点和边进行更新操作，最后新值会被写回磁盘。每次处理一个interval中的点，interval对应的shard被加载进内存称为memory-shard，剩下的shard称为sliding-shard，每个shard上会维护一个滑动窗口覆盖对应interval中点的出边信息，这些出边信息也需要被加载进内存。在处理下一个interval的时候为了获得出边信息每个shard的窗口往后移动即可，详细过程如图 6-4-5所示。这种数据布局和计算模型可以保证每次计算的I/O是顺序的，整个过程磁盘读操作和写操作的数目也是一样的。

图6.29

图 6-4-5 行滑动窗口计算模型[4]

GraphChi是第一个研究如何避免边的随机访问的图系统，能够进行高效的基于磁盘的图计算任务，在单机上处理十亿级条边级别的图数据，并可达到和分布式系统相当的性能。同时在GraphChi的设计中存在一些缺陷，例如PSW有四个问题：为了更新一个shard中的点和边，它们的入边必须全部加载到内存，这就使得前面的三个过程不能相互交叠；对所有shard文件内的边，如果源点和目标点都在同一个interval中会导致顺序的执行，阻碍了完全的并行性；每个迭代的过程中，会有大量的边需要写回硬盘，如果图的数据量非常大并且存在很多个迭代过程，那么GraphChi会有显著数量的I/O；尽管可能一个查询只需要访问图的一小块数据，它还是会在第一轮迭代的时候把整个图读一遍，从线程数量上将或者整个的硬件资源上讲它的扩展性不好。

二、X-Stream系统

X-Stream单机图计算系统[6]在SOSP’13上被提出，X-Stream提出以边为中心的计算思想，用流的方式处理外存或者内存中的边，提高访存的连续性，充分利用存储设备的带宽来提高性能。

以点为中心的图计算系统通常会涉及大量的随机访存行为，为了优化访存，需要根据点集对边数据进行排序等处理，以期在随机访存和连续访存中获得平衡。X-Stream发现用流的方式顺序访问所有的存储介质（包括主存、SSD和磁盘）能够比随机访存取得更大的带宽利用率，图结构中边集通常要比点集大得多，对边和更新数据的访问决定了处理过程的开销，因此将边以流的方式进行处理会比随机访问更有优势。基于此，X-Stream提出了以边为中心的scatter-gather计算模型，将状态存放在点中。当点的状态无法全部加载进内存时，为了减少对点的随机访问，X-Stream还设计了streaming-partition划分机制对图进行划分，相比于GraphChi大大减少了预处理时间开销。这种处理方式在核内和核外两种情况下都能获得较好的性能，并且扩展性较强。

流处理划分策略。X-Stream使用以边为中心的计算模型，并且所有的状态都保存在点中，当以流的方式将边从外存加载进内存处理的时候，对点的访问是随机的，理想的状况是将点全部加载进内存，但是实际情况中点往往无法全部放进内存，这就需要对点和边进行一定的划分。X-Stream设计了streaming-partition数据结构在预处理的时候对图数据进行划分，每个partition包含一个点集、一个边表和一个更新表，见图 6-4-6。这些点集互斥，边表存放相应点集中点的所有出边，更新表存放部分入边，因为不涉及边的排序，在预处理的时候只用消耗很小的时间。实际处理过程中每次对一个partition进行处理，边和更新都以流的方式传输。

图 6-4-6  X-Stream图划分示意图[6]

以边为中心的scatter-gather计算模型。X-Stream实际执行过程中分为scatter、shuffle和gather三个阶段。如图 6-4-7所示，在scatter阶段，X-Stream以流的形式从磁盘取出相应划分区域的边，对每条边的源点应用定义的操作计算，如果需要将产生的更新传递给目标点，则会把更新信息通过出边添加到更新表进行传递。shuffle阶段对前面产生的更新进行分类，将总的更新表打散写到对应的划分当中。实际执行的时候为了减少scatter的随机写更新，将shuffle阶段融合到scatter阶段的最后，采用双缓冲区策略，每个划分块在scatter阶段把更新写到缓存，当scatter阶段处理完所有边之后进入shuffle阶段，按照前面讲的在缓存中对更新分类，某些情况下可以避免更新写回直接提供给gather阶段。在gather阶段，同样需要从磁盘读取更新表，更新对应点的状态值。

图 6-4-7  X-Stream的scatter-shuffle-gather执行过程[6]

总的来看X-Stream的设计使得对点的随机访问发生在小而快的高层存储结构中，对边的访问和更新安排在大而慢的存储结构中，通过流的方式进行顺序访从而存取得最大化的吞吐量。相比于GraphChi[4]，X-Stream对边的顺序访问，能够充分利用存储介质的带宽，同时预处理阶段无序对边进行排序处理，避免了额外的巨大开销，因此能够获得较好的图处理性能。对于Streaming partition的划分策略，虽然partition的数量很小并且不需要对边进行排序，然而选择性调度策略在这样的划分下不适合，在很多只有部分点需要被使用的迭代过程中，缺乏相应的调度策略会导致较大的性能损失。在scatter-gather的计算过程中需要先产生更新表才能更新，会有多次对边的读写操作，比如X-Stream需要在scatter阶段读取边的信息产生更新，然后在gather阶段读取更新，因此总共有三倍于边数目的I/O通信，这对性能也有很大的影响。

三、PathGraph系统

PathGraph单机图计算系统[16]于2014年在ACM/IEEE高性能计算大会(SC’14)上被提出，该系统提出了以路径为中心（path-centric）的图计算方法，并设计了以路径为中心的压缩存储结构来提升计算过程中的局部性和数据访问的连续性，从而加速图计算任务。

PathGraph发现迭代的图计算算法通常有三个特点：（1）每个点在执行的时候需要它所有的入边和出边以及邻居节点的数据；（2）对每个点执行的迭代计算收敛之前必须有沿着它的边遍历整个图的过程；（3）整个图的迭代计算只有在所有的点完成了迭代计算才会收敛。一般的以点为中心或者以边为中心的图计算系统在处理迭代的图计算算法时会存在大量的随机访存，对大图数据的随机划分也会破坏局部性特征，导致大量的分块之间的通信开销。基于此PathGraph提出了以路径为中心的图划分和计算模型，优化了图数据存储结构，并能够在单机上处理十亿条边的真实图数据，整体性能优于GraphChi[4]和X-Stream[6]。

不同于以点为中心（vertex-centric）和以边为中心（edge-centric）的计算模型，以路径为中心的抽象是将原始的图进行基于深度优先遍历树的划分并对每个划分沿着树的路径来计算从而提升图计算性能。在这种方法下，每个划分包含一个前向遍历树和反向遍历树，划分与划分之间可以并行的进行迭代计算，从而缩短了完整的一轮迭代的时间，见图 6-4-8。一轮迭代分为scatter-gather两个阶段，并提供了两个path-centric的编程抽象，分别为path-centric scatter和path-centric gather函数，它们能够提供给用户来定义遍历每个树要执行的算法，用户同样能够定义点更新函数，在遍历的过程中由path-centric函数执行。在scatter阶段活跃点将自己的状态沿着前向遍历树传播给邻居节点，而在gather阶段活跃点通过逆向遍历树从邻居节点收集数据重新计算新值，详细过程见图 6-4-9。在每一轮的scatter阶段后会紧跟一个同步操作，对划分之间共有的边缘节点进行归约，保证下一轮迭代使用的是最新的值。以路径为中心的计算模式在每个遍历树内按照遍历的顺序访问各个节点，在遍历树之间是并行处理的，这种处理方式符合很多迭代的图算法搜索整个图的过程，呈现出很好的数据局部性和并行性，唯一需要同步的地方是边缘节点的同步，每轮迭代时间只受限于最慢的一个划分，大大缩短了整体收敛时间。

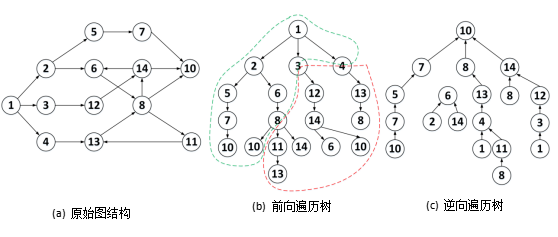
图6.32

图 6-4-8  PathGraph深度优先遍历树划分[16]

图 6-4-9  PathGraph遍历树的并行处理过程[16]

在大规模图数据的存储方式上面，传统的以点为中心或者以边为中心的方案是将图划分为一系列的分片，将点和出边或者入边按一定顺序放在一起存储，当一个分片被加载到内存中的时候会有大量的点和边在计算中没有被使用，导致局部性差和资源浪费的问题。为了进一步优化以路径为中心的计算模式的局部性，PathGraph设计了一个以路径为中心的压缩存储结构，包含基于深度优先遍历顺序的邻接表压缩存储以及基于遍历树的边块存储方式。其中涉及对点的ID编码压缩，邻接表压缩和块索引压缩等技术，节省了存储空间，增强了以边为中心的计算访问磁盘的连续性，进一步提高了带宽利用率，提升了在磁盘中查找大图数据中点边信息的速度。

PathGraph的以路径为中心的计算方法能够大大提升迭代图算法处理超大规模图的速度，这种方法很好的挖掘利用了图的局部性特征，同时高效的压缩存储方案加速了图数据的访问。PathGraph最终能够在一系列迭代图算法的执行上同时优于以点为中心和以边为中心的图计算系统。

四、GridGraph系统

GridGraph[17]在ATC’15上被提出，是一个在单机上处理大规模图数据的系统。GridGraph对图数据采用两层划分策略，将点进行一维划分，边划分为二维网格，同时在运行时进一步对边进行粗粒度的动态划分以提高访存效率，执行模式上采用了新颖的双滑动窗口技术，并且提供了灵活的选择性调度策略优化。该系统利用外存进行图计算，优于当前最好的核外系统，并可获得同分布式系统相当的性能表现。

单机图计算系统GraphChi[4]将图划分为shards存放在磁盘上，利用并行滑动窗口的技术对图进行处理，shard中边需要按照源点排序，预处理时间开销巨大，并且多个shard之间存在大量分段访问，带宽利用不足；X-Stream[6]基于以边为中心的计算模式，采用流的思想将边从磁盘加载到内存中进行计算，scatter-shuffle-gather计算过程中涉及到边数量级别的大量更新写回，在此过程中会触发较多的I/O，严重影响系统的性能。为此GridGraph设计了两层划分策略，在预处理过程中进行一个细粒度划分，得到一维分区的顶点块chunk和二维分区的边块block。在运行时应用粗粒度划分。通过一种双滑动窗口方法，GridGraph在以流的方式处理边同时进行顶点的更新，从而减少了计算所需的I/O量，通过选择性调度可以进一步减少I/O。

图划分策略。GridGraph提出了如图 6-4-10 (a)所示的Grid划分方式。首先，将整个点集划分成相同大小的P个均等的chunk，然后将边集按照格子的形式进行划分，每一行对应在某个chunk内的点相关的所有出边，每一列对应在某个chunk内的点相关的所有入边，通过选择P使得每个块足够小以适合快速存储，当访问与块相关联的顶点数据时，可以确保良好的局部性。具体划分示例如图所示，{1，2}和{3，4}是两个顶点chunk，最后边被分成四块。在实际过程中，利用两层划分策略，调整P使得每个小块能够放进缓存，然后在运行过程中动态的将小块联合成大块优化内存到磁盘之间的访问，如图 6-4-10(b)所示。

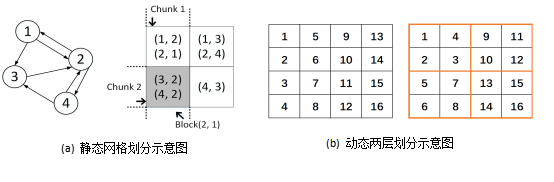
图 6-4-10 GridGraph两层网格划分策略[17]

双滑动窗口（dual sliding windows）。GridGraph设计了streaming-apply执行模型，利用双滑动窗口对边进行处理。如图 6-4-11计算PageRank算法的一次迭代，计算点的更新值需要读取其入边源节点的值，为此从上到下，依次读取该列每个格子内的边进行计算，然后当一列计算完毕后，即完成一个子点集中点的值的计算，窗口滑动到下一列，继续进行计算，直至所有的格子都遍历完毕。像这种读取源顶点数据并写入目的顶点数据的情况，GridGraph选择从上到下地流式处理每一个边块，目标顶点块缓存在高速存储器中，磁盘写入操作被聚集和最小化，点的数据访问的局部性也有提升。基于streaming-apply执行模式的即时就地更新策略，使得结果对随后的顶点立即可见，从而加速迭代算法的收敛，而且不会产生中间的更新结果，极大地减少了I/O。

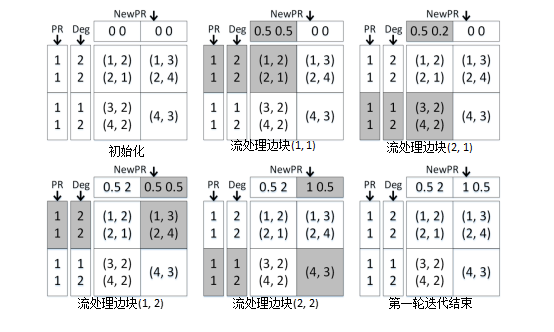
图 6-4-11  PageRank算法一轮迭代执行过程[17]

总结来看，Gridgraph使用了划分后的点块和边块以及双滑动窗口算法来处理硬盘上的图数据，它能进行选择性的调度避免处理未激活的边块，减少必要的I/O数量。Gridgraph提出了streaming-apply执行模型，在流动处理边的同时对点进行更新，使用原子操作解决更新过程中的数据竞争。GridGraph在内存和带宽上具有很好的扩展性，并且优于GraphChi[4]和X-Stream[6]等基于外存的图计算系统。部分情况下GridGraph的性能与分布式图计算系统相当，GridGraph尤其适用于云环境下的图计算。