导读

由于图计算能够用于分析数据之间的关联关系，因此其在互联网应用、科学计算、社会计算、商业计算等诸多领域得到应用广泛，已经成为大数据处理的主流模式之一。当前，随着互联网的快速普及，社会的数字化变革以及经济的快速发展，表达数据关联性的图数据的规模正在呈爆发式增长。如何有效地分析海量图数据已引起工业界和学术界的广泛关注，成为大数据处理的关键问题。本章的目标在于让读者了解图数据本身的组织特点，理解图计算对计算机系统的重要挑战，熟悉图计算系统的编程模式和运行时系统，掌握典型图计算算法的特征和应用方式和图计算系统性能评估的各种方法。具体来说，本章首先希望读者能了解图计算的背景和意义，并宏观了解图计算流程以能够初步使用图计算系统进行数据分析；其次介绍图计算随机数据访问和高访存/计算比等特征给传统计算机系统带来的挑战，并详细阐述现有图计算系统采用的主流编程模型和运行时优化方法；然后本章将介绍现有的各类典型图计算系统和硬件加速技术；接着将介绍典型图拓扑分析和图数据查询等算法是如何解决现实问题的；最后，本章将介绍现有的图计算系统性能评估方法。

6.1 图计算背景

6.1.1 图计算简介

图在结构和语义等方面具有很强的表达能力[1]，能够很好的描述事物之间的关联性。在实际生活中，诸多场景都采用图来描述关联关系。例如社交网络将用户作为图顶点，而用户好友关系等作为边来构成图；城市道路系统将路口作为图顶点，道路作为边来构成图等。关联分析是大数据处理的关键操作之一。图计算是以图数据结构来抽象描述事物之间的关联性，并且在该数据结构上进行处理分析的模式。通常，在图计算中，基本的图数据结构为：G =（V，E，W），其中V，E和W分别表述图的顶点、边以及权值。在此计算过程中，顶点和边都会包含计算过程中的状态数据，然后通过对每个顶点和边进行一系列的迭代计算来完成状态数据的更新。图计算的结果为图中所有顶点和边的最终状态的聚合。

图计算能够挖掘事物之间潜在不易洞察的行为和联系，而这些关联性很难使用传统数据库来描述。这使得图计算在经济建设、国防安全和社会生活等的方方面面都能够发挥重要的作用。例如，图计算在互联网金融行业和反欺诈有着重要的意义。尤其在当前普惠金融的市场环境下，线上欺诈风险变化非常迅速，而且数据量巨大。然而，传统的反欺诈手段无法根据数据之间复杂的关系挖掘出潜在的群体欺诈。因此，它可以通过描述事物关系的图来有效解决。

在银行借贷中可以通过不一致验证来判断某人的欺诈风险，在如图 6-1-1所示的图结构中，若借款人Abel和借款人Bob填写的公司电话相同，但是公司却不相同，那么这样的借贷可能存在风险。同时，在异常检测中可以通过分析找出图中的异常图顶点和图结构，或者异常的图结构变化，下面简单介绍静态分析和动态分析两类方法。

图 6-1- 1 一致性检测

静态分析是指在静态的图结构中找出异常图顶点（例如，异常子图等），在图 6-1-2所示的图结构中，虚线框中的顶点紧密度非常强，那么可能是欺诈组织，针对这样的异常结构，可以进行进一步分析。

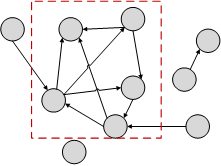
图 6-1- 2 静态分析

动态分析，即分析图结构随时间变化的趋势。如果假设图结构在短时间内不会发生较大变化，否则说明该变化存在异常。图 6-1-3表示了某一时段图结构随时间的变化情况，可以看出图顶点之间的关联性发生了较大的变化，则该变化存在异常。

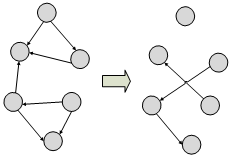
图 6-1- 3 动态分析

由此可见在反欺诈的场景中，图结构能够聚合各类数据源，通过对图结构进行分析，进而发现存在的风险，提高规避风险的效率。

6.1.2 图计算特点

随着互联网的高速发展，图数据规模正在爆发式增长。根据2016年12月Facebook最新发布数据显示，其社交网络已超过17.1亿个图顶点以及1千亿条边。如果考虑用户的“点赞”信息，图的边及其关联信息将达到万亿级规模以上。可见随着对数据关联性分析需求日益增加的同时，图数据的规模也在日益增大。同时，由于图结构的非规则特点，大图计算除了拥有大数据处理的基本特点外，还存在诸多新的挑战。近年来，图计算领域相关研究呈现爆发式增长，已经成为大数据处理领域的研究重点。

首先，图计算具有数据局部性差的特点。由于图结构是不规则的，因此图数据访存缺乏好的局部性，然而，在现有的计算机体系架构上，局部性的好坏往往决定了程序性能的好坏，因此，如何提升图计算数据局部性，是提高图计算性能的重要方面。另外，对这种非规则的图数据如何进行有效的划分，从而达到存储、通信和计算的负载均衡的效果是非常棘手的问题。一旦划分不合理，计算节点间不均衡的负载将会使系统的扩展性受到严重限制，处理能力也将无法符合计算系统的规模。

其次，图计算是图结构驱动的计算。由于在图算法执行中，图算法是根据图结构来进行处理，而不是直接通过程序中的代码展现出来，因此它在不同的图结构上执行相同的算法会得到不同的计算性能。从而，如何使得不同图结构在同一个系统上都有较优的处理性能也是需要解决的问题。

最后，图计算存在高访存/计算比的特征。由于图数据规模巨大，内存中往往不能完整的存下图数据。这使得计算中磁盘的I/O必不可少。然而，大部分图算法都需要进行多次迭代，每次迭代需要遍历整个图结构，同时迭代中计算量相对较小。这导致高的访存/计算比。另外，由于图计算的局部性差，这使得计算在等待I/O上花费了巨大的开销。

6.1.3 图计算实例

下面通过图计算系统Gridgraph上如何执行网页排名算法（PageRank）任务来解释图计算执行的主要过程。一般情况下，为了提高数据访存效率以及内存大小的限制，首先它需要对原始图数据进行预处理。Gridgraph采用一种两层划分策略，将点进行一维划分，边划分为二维网格，同时在运行时进一步对边进行粗粒度的动态划分以提高访存效率。在对图数据进行预处理完成后，它依次将图数据块加载到内存中，通过图计算系统的编程模型实现图算法来进行相应的计算。Gridgraph采用streaming-apply执行模型。它在流动处理边的同时对点进行更新。本质上它是以边为中心的计算模型。PageRank算法在Gridgraph上的实现如图 6-1-4所示。首先，它通过函数CONTRIBUTE(e)来遍历边，将源图顶点值传递到目的图顶点，并更新目的图顶点的值。然后，它通过对图顶点的遍历来计算出这一轮计算的图顶点最终值，并将新旧值的差值∆返回。最终，Gridgraph通过∆值来判断算法是否收敛。

图 6-1-4  PageRank算法

6.2 图计算并行编程模型

为了简单高效得实现并行图计算，目前主流图计算系统采用四种编程模型：以点为中心的编程模型、以边为中心的编程模型、以路径为中心的编程模型和以子图为中心的编程模型。其中以路径为中心的编程模型可以看成是以子图为中心的编程模型的特例。

6.2.1 以点为中心的编程模型

由于图数据结构内部存在复杂的依赖关系，图计算系统存在不易扩展和难以并行化的问题。为了解决这些问题，需要提出一种适合图计算的编程模型作为系统设计的基础。Google在2010年发表的Pregel [2]计算框架所采用的TLAV （Think Like a Vertex）思想，正是针对图计算的特点所采用的一种新式编程模型。该模型把计算范围限定在图数据中的单个点，即从单个点的角度考虑图算法的执行过程，包括每个点上的计算以及相邻点之间的消息传递。这样各个点可以实现相互独立的计算，从而进行细粒度的并行。

如图 6-2-1所示，最早的TLAV是建立在BSP（Bulk Synchronous Parallel）模型之上,即把计算过程分割为多个超级步，超级步之间通过屏障（Barrier）来保证信息被同时传送和接受，从而避免了数据竞争和死锁。但以点为中心的模型并不局限于上述的同步执行模型，还支持异步执行模型。与同步执行模型不同的是，异步执行模型不需要屏障来限定超级步之间的信息传输，即每个点的更新值可以在当前的超级步中立即可见，从而加速算法的收敛速度。但是，异步执行模型需要考虑数据竞争、一致性等问题。

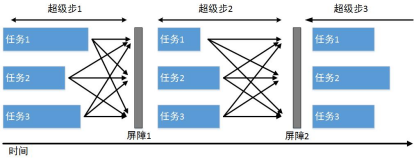
图 6-2-1  BSP模型

以点为中心的模型处理图数据中的每个点都需要采取三种操作：收取信息，更新信息和分发信息。如图 6-2-2所示，收取信息操作是点获取所有邻接点更新的状态信息，并为点的状态更新做准备。更新信息操作是点根据收取邻接点的状态信息来更新自身的状态。分发信息操作是点把更新的状态信息通过边传送出去。根据编程实现上述操作的方式不同，以点为中心的编程模型被分为一阶段编程模型、二阶段编程模型和三阶段编程模型。

图 6-2-2 以点为中心的模型处理点的三种操作

一阶段编程模型中，用户定义单个目标函数来实现上述的三种操作。比如Pregel[2]系统，用户定义处理点的Compute()函数，该函数中，每个点获取状态信息并更新自身的状态，最后把更新的状态信息传送到邻接点，如图 6-2-3所示。采用一阶段编程模型的典型代表系统有Pregel[2]，GPS[3]等等。

图 6-2-3  Compute() 编程模型

二阶段编程模型中，用户需要定义两个函数来实现上述的三种操作，其最具有代表性的模型为Scatter-Gather编程模型。如图 6-2-4所示，Scatter-Gather编程模型定义vertex_scatter()和vertex_gather()两个函数来实现上述的三种操作。vertex_scatter()函数把点的状态信息传送出去，而vertex_gather()函数收集邻居点的状态信息并更新自身的状态。该模型的每个函数的输入对象为图数据中的点，其终止的条件为所有的点不再产生更新。此外，二阶段的编程模型还有Scatter-Combine模型、Gather-Apply模型等等。采用二阶段编程模型的典型系统有GraphChi[4]等。

图 6-2-4  Scatter-Gather编程模型

三阶段编程模型把上述的三种操作分别用三个函数来实现，其典型代表为GAS（Gather-Apply-Scatter）模型(如图 6-2-5所示)。在该模型中，每个点首先在vertex_gather()函数中聚集其所有邻居点的状态信息，然后在vertex_apply()函数中更新自身的状态信息，最后使用vertex_gather()函数把更新的状态信息传送出去。采用三阶段编程模型的典型系统有PowerGraph[5]等。

图 6-2-5  Gather-Apply-Scatter编程模型

以点为中心的编程模型实现的图计算系统需要对顶点数据和边数据进行访问操作，如图 6-2-6所示，数据访问过程存在大量的随机访存操作，这将导致较大的时间开销。由于现代计算机体系结构的特点，随机访存往往比顺序访存的性能低。例如，访问内存、固态硬盘和磁盘，随机访存比顺数访存分别慢 2倍，20倍和500倍[6]。因此如何采用顺序访存进行图计算的问题受到业界广大的关注。同时，以点为中心的编程模型需要对原始的图数据进行排序等预处理操作，这也增大总的时间开销。

图 6-2-6  以点为中心模型的访存情况

6.2.2 以边为中心的编程模型

如前所述，以点为中心的编程模型存在大量的随机访存和排序预处理等问题，为了解决这些问题，以边为中心的模型被提出[6]。

图 6-2-7给出了以边为中心的Scatter-Gather模型实例，其函数输入不再是图顶点，而是图中的边。在该模型中，它遍历所有边，将源顶点的最新信息通过边传送出去以更新目的顶点。

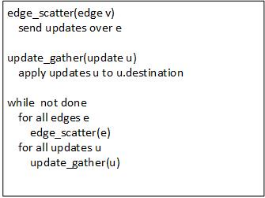
图 6-2-7 以边为中心的Scatter-Gather模型[6]

以边为中心的模型不再采用随机访存的方式来访问边数据（如图 6-2-8），而是采用顺序访存的方式。X-Stream[6]通过试验证明以边为中心模型运行算法比采用以点为中心模型运行算法在处理速度上提高了2到3倍。同时，以边为中心的模型不需要对原始的图数据进行排序等预处理操作，从而降低了时间开销。

图 6-2-8  以边为中心模型的访存情况

6.2.3 以路径为中心的编程模型

TripleGraph [16]提出了以路径为中心的编程模型，与以边为中心的编程模型相似，该模型同样采用的顺序访存替代随机访存，以此可以提高定义和执行图局部更新的收敛性。

以路径为中心的编程模型包含两个基本操作，如图 6-2-9所示，分散（Scatter）操作和整合（Gather）操作。主函数通过迭代器对所有节点循环执行Gather或Scatter操作。TripleGraph将树中需要遍历的节点集看作路径。

图 6-2-9 路径为中心计算模型

如图 6-2-10所示，Scatter操作接收一个节点的状态并利用它沿着路径生成更新。在每次迭代计算的Scatter阶段，读取该节点和该节点的数据字段，更新数据字段中的后续节点，然后读取后续节点中某一节点的目标节点序列，继续更新其数据字段。在每次迭代结束时，系统进行数据的同步。

图 6-2-10  Scatter算法

Gather操作则是获取一个节点的所有入边，并利用入边信息来更新该节点的数据，如图 6-2-11所示。Gather操作以节点的入边作为输入，但是沿着节点的反向路径进行计算。

图 6-2-11  Gather算法

在每个区间内，Gather操作或者Scatter操作读取节点集合，利用路径数据流信息，产生更新流。如若输出流中目的节点属于其它区间，将其更新信息添加到相应区间的待更新序列中。当本次迭代过程结束时，同步步骤即可开始。对于每一个区间，读取节点集合，将更新列表的数据读出并计算出节点集合新的数据。最后将节点的权重更新为新值。与GraphChi将节点的新值分配到边权重中不同的是，TripleGraph不需要改变边的权重。

图数据处理是基于其允许顺序访问和更新边的数据。TripleGraph并不和X-Stream一样需要较多的随机访问节点数据。在计算的过程中，Gather和Scatter操作都是顺序地将数据从多个缓冲区读入，或者是将数据分散，写入到多个缓冲区中。Gather和Scatter作用是将数据聚集在一起，或分散到给定的缓冲集中。

以路径为中心的并行计算模型能够顺序处理大规模图数据，在图数据处理过程中只需要很少量的随机数据的读写。顺序读写不仅减少了数据在定位时所耗费的时间，同时对减轻了系统在I/O上面的负载。另外，常规的算法如X-Stream的每次迭代计算需要三步骤：Gather，Shuffle和Scatter。而该模型只需要两个步骤：Gather或Scatter。因此，以路径为中心的模型简化了迭代计算的步骤，减少了系统迭代计算的时间，加快了算法的执行速度。

6.2.4 以子图为中心的编程模型

以点或边为中心的编程模型是一种细粒度的编程模型，由于其状态信息在每个超级步内只能被传播一跳，导致某些特殊的算法不能有效的执行。例如，文章[7]在图数据UK-2005和SK-2005数据集[5]上采用以点为中心的模型来运行SCC（Strongly Connected Components）算法，分别需要4546和6509个超级步，其收敛速度十分缓慢。针对细粒度编程模型的局限性，一种以子图为中心（Subgraph-Centric，也称为以块为中心Block-Centric）的粗粒度编程模型被提出[9]，且子图是由相互关联性较强的图顶点构成。

以子图为中心的模型先把图数据划分为不同的子图，然后更新子图中所有的点直到子图收敛，最后把子图更新的状态信息传送到其它子图。如图 6-2-12所示，以子图为中心的模型的函数block_update()处理的对象为子图整体，该函数终止条件为子图中的点不再产生更新。

图 6-2-12 以图为中心的模型

例如，图 6-2-13（a）和（b）分别为Connected Component算法（简称为CC算法）在以点为中心的模型和以图为中心的模型上执行的情况。当采用以点为中心的模型来运行算法，系统需要7个超级步才能够使算法达到状态收敛，而采用以图为中心的模型来运行该算法，系统仅仅需要3个超级步便可以使算法达到状态收敛，后者大大减少了超级步的数量从而降低了计算的时间。同时，文章[10]在USA Road数据集[11]上进行SSSP（Single Source Shortest Paths）算法的测试，采用以点为中心的模型运行算法需要10789超级步（2832s），而采用以子图为中心的模型运行算法需要59超级步（11s），后者在计算速度上提高了两个数量级。以子图为中心的编程模型可以加快算法收敛的速度，但该模型存在一些挑战，比如对图数据进行子图划分等问题。采用以子图为中心的编程模型典型的系统有Blogel[10]，Giraph++[9]，GoFFish[12]和BlockGRACE[13]等。

图 6-2-13 执行算法CC情况