Reliability of Frame and Shear Wall Structural Systems. I: Static Loading

Ahmed Ghobarah

Abstract:

An efficient and accurate algorithm is developed to evaluate the reliability of a steel frame and reinforced concrete shear wall structural system subjected to static loading. In a companion paper, the algorithm is extended to consider dynamic loading, including seismic loading. The concept integrates the finite-element method and the first-order reliability method, leading to a stochastic finite element-based approach.

In the deterministic finite-element representation, the steel frame is represented by beam-column elements and the shear walls are represented by plate elements. The stiffness matrix for the combined system is then developed. The deterministic finite-element algorithm is verified using a commercially available computer program. The deterministic algorithm is then extended to consider the uncertainty in the random variables. The reliability of a steel frame with and without the presence of reinforced concrete shear walls is evaluated for the strength and serviceability performance functions. The results are verified using Monte Carlo simulations. The algorithm quantitatively confirms the beneficial effect of shear walls, particularly when the steel frame is weak in satisfying the serviceability requirement of lateral deflection. The algorithm can be used to estimate the reliability of any complicated structural system consisting of different structural elements and materials when subjected to static loading. The procedure will be useful in the performance-based design guidelines under development by the profession.

keywords: Limit states; Simulation; Shear walls; Static loads; Steel frames; Finite element method.

Introduction

The realistic reliability analysis of complicated structural systems consisting of different types of structural elements and materials is a major challenge to our profession. In most cases, the limit state or performance function (a functional relationship between the load- and resistance-related variables and the performance criterion) is implicit in evaluating the reliability of such systems. The analytical technique most frequently used to capture the mechanical behavior of complicated structural systems consisting of different materials appears to be the finite-element method (FEM)-based approach. Finite-element analysis is a powerful tool commonly used in many engineering disciplines to analyze simple or complicated structural systems. With this approach, it is straightforward to consider complicated geometric arrangements，various sources of nonlinearity, different materials, and the load path to failure. However, the deterministic finite-element method fails to consider the uncertainty in the variables, and thus cannot be used for reliability analysis. On the other hand, the available reliability methods fail to represent structures as realistically as possible. If the basic variables are uncertain, every quantity computed during the deterministic analysis is also uncertain. The currently available reliability methods can still be used if the uncertainty in the response can be tracked in terms of the variation of the basic variables at every step of the deterministic analysis. To capture the desirable features of these two approaches, they needed to be combined, leading to the concept of the stochastic finite-element method (SFEM) (Haldar and Mahadevan 2000b)。

The SFEM algorithm for frame structures has been developed by several researchers. However, the main drawback of frame structures is their inability to transfer horizontal loads (e.g., wind, earthquake, and ocean waves) effectively. They are relatively flexible. To increase their lateral stiffness, bracing systems or shear walls are needed. Haldar and Gao (1997) Attempted to consider bracing systems in a steel frame structure. They used truss elements in their model. However, there has not been an attempt to consider shear walls, represented by two dimensional plate elements, in a frame in the context of SFEM.

Numerical Examples

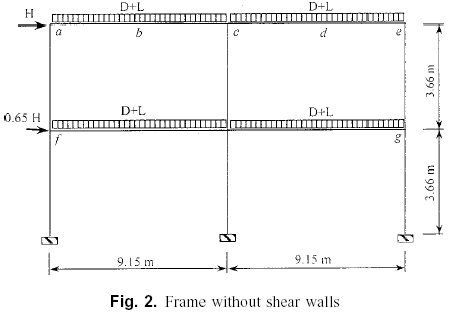
To investigate the effect of shear walls on the overall reliability, both a frame without shear walls and a frame with shear walls are studied in this study. All loads are applied statically. The reliability of the frame with and without shear walls is evaluated using the proposed algorithm. The accuracy of the proposed algorithm is established using Monte Carlo simulations.

Reliability Analysis of Frame without Shear Walls

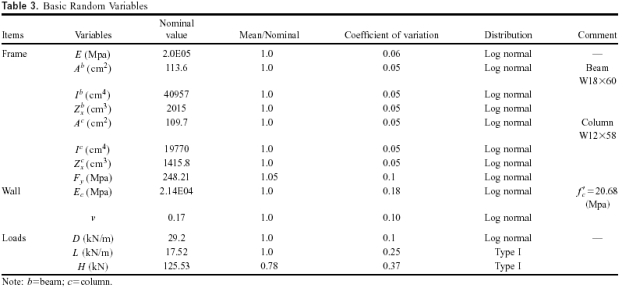
A two-story two-bay frame shown in Fig. 2 (Fig. 1 without the shear walls) is considered first. A36 steel is used. The statistical characteristics of the cross-sectional and material properties required for the reliability analysis are given in Table 3. The frame is subjected to dead, live, and horizontal loads. The statistical properties of these loads are given in Table 3.

For the strength limit state, the reliability of the most critical beam at node e and the most critical column at node c are evaluated using the proposed algorithm with the performance functions represented by Eqs. (13) and (14). For the serviceability limit state, the horizontal drift of the top floor at node a and the vertical deflection of the beam at the midspan at node d are checked. In Eq. (20), the prescribed horizontal drift at the top floor is considered to not exceed h/400, where h is the height 006Ff the frame. Thus, 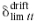 is equal to 1.83cm in this example. Similarly, the prescribed vertical deflection in the midspan of the beam is considered to be l/360 under the unfactored live load, where l is the span length of the beam. In this case,  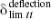is considered to be 2.54cm.

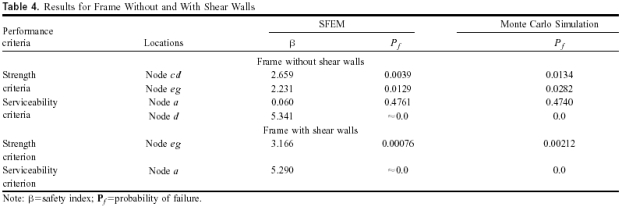
Considering all the random variables given in Table 3, the corresponding reliability indexes and the probabilities of failure at different node points are evaluated. The results are summarized in Table 4. For the frame without shear walls, the probability of failure of the beam is found to be 0.0039, and 10,000 simulations were used to capture this behavior. For the horizontal drift, the probability of failure is close to zero. Considering the practical aspects of supercomputer utilization, 100,000 simulations were used to capture this behavior: The Monte Carlo simulation results are summarized in Table 4.

Reliability Analysis of Frame with Shear Walls

The frame shown in Fig. 2 is reinforced with shear walls as shown in Fig. 1. The statistical properties of two additional variables related to the shear walls, Ec and ν, are given in Table 3. The building is assumed to contain five similar frames connected by rigid diaphragms at the floor levels. Only the center frame of the building is assumed to have shear walls. Although the physical thickness of the shear wall is 12.7cm,considering the presence of five similar frames and the rigid behavior of diaphragms, the effective thickness per frame is assumed to be 2.54 cm in this study. The combined system is subjected to the three static loads given in Table 3. After the tensile stress of each shear wall exceeds the prescribed tensile stress of concrete, the degradation of the shear wall stiffness is assumed to be reduced to 40% of the original stiffness.

The probability of failure of the combined system is calculated using the proposed algorithm. For the strength limit state, the probability of failure of a column, represented by Node eg in Figs. 1 and 2, is estimated. For the serviceability limit state, the horizontal deflection at the top of the combined system (point a in Figs. 1 and 2) is evaluated. The results are summarized in Table 4.

As before, 10,000 simulations are used for the strength limit state and 100,000 simulations are used for the serviceability limit state. For both the strength and serviceability limit states, the reliability indexes estimated by the proposed algorithm and the Monte Carlo simulation technique are similar. The results clearly indicate that the proposed algorithm can be used to estimate the probability of failure of a combined system consisting of frame and shear walls under static loading. The reliability of the column did not change significantly due to the presence of shear walls. However, the horizontal drift at the top of the frame reduced significantly and the probability of failure of the combined system in serviceability became almost zero. This is expected. For the combined system, the controlling limit state has changed from serviceability to strength. This simple example clearly demonstrates the beneficial effect of shear walls in carrying horizontal loads. It also demonstrates that the proposed algorithm can be used to estimate the reliability of a complicated structural system under static loading conditions, broadening the application potential of reliability methods.

Conclusions

An efficient and accurate algorithm is developed to evaluate the reliability of a steel frame and RC shear wall structural system. The steel frame is represented by beam-column elements and the shear walls are represented by plate elements. A stochastic finite element-based approach consisting of the reliability approach, the first-order reliability analysis procedure, and the finite-element method is proposed. The reliability of a frame with and without shear walls is evaluated for the strength and serviceability performance functions. The results are verified using the Monte Carlo simulation technique. The proposed stochastic finite-element-based algorithm is reasonable for evaluating the reliability of a combined system consisting of frame and shear walls for static loading. It gives similar results for both the strength and serviceability performance functions compared to the results from Monte Carlo Simulation. As expected, this study showed that the reliability of a frame for horizontal deflection could be significantly improved with the help of shear walls. The proposed algorithm to evaluate the reliability of a combined system consisting of steel frames and RC shear walls for static loading is very unique. It produces accurate and efficient results, and can be used in the future to evaluate the reliability of complicated structural systems. The proposed algorithm demonstrates how reliability methods can be applied to evaluate the risk of a real structural system capturing its realistic mechanical behavior. The procedure will be useful in the performance-based design guidelines under development by the profession.

References

[1]  Chaallal O, Nollet M-J, Perraton D. Shear strengthening of RC beams by externally bonded side CFRP strips. Journal of Composites for Construction, ASCE 1998;2(2):111–3.

[2]  Spadea G, Bencardino F, Swamy RN. Structural behaviour of composite RC beams with externally bonded CFRP. Journal of Composites for Construction, ASCE 1998;2(3):132–7.

[3]  Saadatmanesh H, Ehsani MR, Li MW. Strength and ductility of concrete columns externally reinforced with fibre composite straps. ACI Structural Journal 1994;91(4):434–47.

[4]  Saadatmanesh H, Ehsani MR, Jin L. Seismic strengthening of circular bridge pier models with fibre composites. ACI Structural Journal 1996;93(6):639–47.

[5]  Saadatmanesh H, Ehsani MR, Jin L. Seismic retrofitting of rectangular bridge columns with composite straps.Earthquake Spectra 1997;13(2):281–304.