摘要

本文主要对受压区由钢纤维（SF）高强度混凝土（HSC）和受拉区由标准混凝土构成的双层受弯预应力梁的分析。这类梁的研究对钢筋混凝土结构设计是很重要的，特别是纤维体积率的计算就如同普通混凝土中配筋率的计算那么重要。换句话说，这些构件是由高性能混凝土（HPC）构成的。首先对于预应力构件，更趋向于用更有效的高性能（HPC）结构取代标准强度混凝土（NSC）构件。其次给出了应用于双层预应力梁的高强混凝土强度等级下限的定义。实验结果表明，钢纤维（SF）对梁的弹性变形几乎没有影响。然而，因为受弯构件增加了塑性耗能（PED）的潜能，它的极限变形能力增加了。相比于单层高强混凝土梁，受拉截面处改用标准强度混凝土的双层预应力梁，它有助于截面塑性耗能能力增加20%。为了保证需承受动力荷载的预应力梁截面有足够的延性，这里提出了最低钢纤维（SF）体积率。在混凝土基体产生裂缝时，纤维承受拉应力。提出了所需延性的应变量即钢纤维体积率的计算的设计方法。同时也提出了说明这个方法效率的一个数值例子。

关键词：标准强度混凝土，高强混凝土，钢纤维，高性能混凝土，双层预应力梁

1、 引言

在过去的数十年，在混凝土结构中，高强混凝土（HSC）是一个有趣且富挑战性的创新。因为这种材料不仅仅只是一个学术研究的课题，而且正被逐渐应用于实际结构。现在高性能混凝土（HPC），代替高强混凝土（HSC）成为一个更普遍的话题。许多实验研究的目的是研究高强混凝土（HSC）和高性能混凝土（HPC）结构的性能。因为在2002年国际研讨会上针对高强混凝土（HSC）和高性能混凝土（HPC）的定义并没有最终达成协议。所以作者给出了高强混凝土（HSC）的定义。根据该定义，混凝土被界定为高强混凝土（HSC）须满足下列条件：混凝土抛物线图在卸载时没有分支；混凝土“应力——应变”函数的最小指数；混凝土在受压时的最小延性参数。另外，据报道，高强混凝土（HSC）的强度值可由相应于由弹塑性石材转变为脆性材料所需的强度来刻画。

根据作者给出的定义，高强混凝土（HSC）的抗压强度应达到fc≥70Mpa。但是，此时材料呈现出完全的脆性性能。为了尽可能地充分利用高强混凝土（HSC）的强度，确保混凝土块必须的延性就要求采取更多的结构措施。为了改善高强混凝土（HSC）的性能，即增加其延性，钢纤维（SF）通常被加入到混凝土基质中。不管怎样，裂缝是出现在受拉区了，因此，他对受弯构件承载能力的提高是不容忽视的。因此，使用由在受压区用钢纤维高强混凝土（SFHSC），在受拉区用标准应力混凝土（NSC）组成的双层梁是合理的。这种做法降低了钢纤维（SF）的消耗，防止了受压截面的脆性破坏，从而形成了一个更有效，更经济的设计方案。

据显示，对于在梁受压区由钢纤维(SF)增强高强混凝土（HSC）塑性的弯曲预应力构件用双层梁是很有效的。此外，用纤维还大大改善了混凝土模块与预应力钢筋间的粘结。而且，对先张法混凝土构件的作用而言，缩短先张法构件的传递长度是钢纤维（SF）的最大作用。这意味着由高强度混凝土（HSC）和标准强度混凝土（NSC）组成的预应力双层梁成了高性能混凝土（HPC）构件。使用钢纤维（SF）也有利于在较大位移阶段消耗能量，从梁的承载能力来看这一点尤为重要。

对由钢纤维混凝土（SFHSC）和标准强度混凝土（NSC）构成的双层预应力梁的设计方法仍然不够发达。而且，在钢筋混凝土结构中这类梁的设计形成了新的问题：

·根据所给的标准强度混凝土（NSC）的等级确定预应力梁的高强混凝土（HSC）的等级；

·预应力截面所需的延性的应变量钢纤维率的计算；

·计算最小和最大的钢纤维体积率。

一般情况下，钢纤维（SF）体积率的选择是基于工程经验，技术要求等的。为了确定钢纤维（SF）体积率，许多实验研究正在进行。钢纤维（SF）体积率将从0.5%到2.5%的变化范围这个方法选择。这个比例的下限值在前面已经介绍。

因为高性能混凝土（HPC）更有效，而且取代了标准强度混凝土（NSC），尤其是在预应力构件中，所以为这类构件的设计形成一个强有力的理论背景很重要。这篇文章将侧重于对上述问题从由钢纤维混凝土（SFHSC）和标准强度混凝土（NSC）构成的预应力梁的观点出发进行理论分析。它是建立在其他研究人员完成的实验研究的基础上的。对现代结构设计，解决这些问题就如同对普通钢筋混凝土（RC）结构的钢筋率计算一样重要。

2、 对双层预应力梁较低高强混凝土（HSC）等级限制的计算

处于受拉区的弯曲钢筋混凝土构件，出现裂缝前，先在混凝土模块中出现塑性变形，同其他受拉材料一样。对受拉区混凝土，符合理想状态的“应力-应变”曲线见图1。

图1.出现裂缝前预应力弯曲构件的性能：（a）受拉混凝土理想“应力-应变”曲线；（b）在外部弯矩作用下构件裂缝极限状态；（c）预应力作用下的裂缝极限状态。

在这个图中各符号意义如下：

fctm一代表混凝土沿轴向拉伸的强度值；

Mr一结构底部预应力区的开裂弯矩；

Xr一受压区相应中性轴高；

M’r一结构顶部开裂弯矩（无筋区）；

x’r一受压区相应中性轴高；

Asp一预应力钢筋束贯穿的截面面积。

结构底部开裂弯矩（见图1.b）

                   其中   ，

例如，对一个给定的矩形梁结构，它的数据如下：

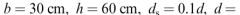
则结构底部的开裂弯矩为

给定能够得到顶部（无筋区）截面的开裂弯矩如下：

许多研究人员都在用实验的方法研究M’r和Mr之间的关系。根据前面的方法，对三根梁进行试验，它们之间的比值从1.252变到1.716（平均值是1.536），它很好地符合了从理论上获得的结果。（见公式（2））

如果一个预应力构件的截面有两层，对顶部高强混凝土（HSC）层的最小混凝土拉伸强度为：

在这种情况下，由于预应力的存在，在负弯矩作用下，裂缝将不再出现在那一层中。这一条件可以用于根据给定的标准强度混凝土（NSC）等级计算高强混凝土（HSC）等级。这个条件也可用来减少顶部（受压区）额外预应力钢筋的使用量。同时，对于一个给定的标准强度混凝土（NSC）的等级，公式（3）定出了可以用于双层梁的高强混凝土（HSC）的等级的最小值。现实中，高强混凝土（HSC）的采用应根据受压区混凝土强度的设计值选定。

3、 无纤维预应力混凝土截面的延性

表3.1定义了混凝土等级从16到90的强度和变形的特点。对应力有σc=0-0.4fcm的混凝土的各个等级的弹性模量也给出了。表中没有包括混凝土的极限弹性变形值为截面延性计算所用。

可以计算上述变形如下：

按照这个公式，对上述混凝土等级的极限弹性变形是（见表2）

对于处于受压区的高强混凝土（HSC）的弹性势能是

为了计算处于受压去的混凝土截面的全部耗能量，混凝土应力—应变关系应当被运用。根据欧拉规则（Euro code）

其中n是根据表3.1确定的指数，εc2是混凝土极限强度状态时的应变。

正如作者在此之前论证的一样，对强度等级大于等于70的高强混凝土（HSC）

n=1.4=常数，εc2=0.0026=常数                       （8）

整个受压区截面消耗的势能是

例如，对于90号高强混凝土（HSC），根据公式（6）

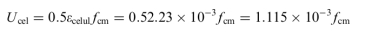
根据公式（9）和公式（8）

延性参数

即其结果接近1.0，就如弹性材料的情况一样。

有人认为根据线性图的上涨（见图2）处于受压区的预应力钢筋变形了。两条直线坐标分歧的坐标是(fFPK01，fPK01/ESP）,终点坐标是（fPK，εSPUL），但极限变形点是εSPUL是未知之数。在这里，fPK是预应力钢筋拉伸强度特征值，fFPK01是预应力钢筋0.1%保证应力的特征值；ESP是预应力的弹性系数设计值；εSPUL是预应力钢筋在极限荷载作用下的变形。

图2. 预应力钢筋拉伸是应力—应变图

接下来，预应力高强钢筋（HSS）的弹性和塑性势能是：

其中

相应的延性系数是

如果预应力梁的钢筋应力那么该截面的拉伸对于塑性耗能几乎没有作用，在这种情况下μSP=1。然而，如果σSP＞fpk01,那么μSP=f（εSPUL）＞1，钢筋最终变形未知数εSPUL应该能计算了。因为这个原因紧接着需要增加一个公式。对于受弯构件，平面假设或截面能量公式都可以用。

4、 最小钢纤维（SF）体积率定义

有两个因素可以使双层预应力受弯截面降低塑性耗能（PED）：

·高强混凝土（HSC）在受压区

·高强钢筋（HSS）在受拉区

很显然应该预防能量耗散，即高性能混凝土（HPC）应当被使用。但是这仅仅是指在受压区合理使用高性能混凝土（HPC），因为在受拉区混凝土的作用是可以忽略的。一般来说，为了改善截面的塑性耗能（PED），会在截面上添加钢纤维（SF）。但是，同样不是在整个截面上添加钢纤维（SF），一方面是因为像上面所说的混凝土的作用在受拉区是可以忽略的，另一方面是因为钢纤维（SF）对预应力钢筋一点不起作用。因而只在混凝土受压区使用钢纤维（SF）已经足够了。此外，只存在于受拉区的标准强度混凝土（NSC）增加了整个截面的延性，随着高强混凝土（HSC）和标准强度混凝土（NSC）等级的不同，它的影响也在增加（见表1）。因此，我们（从结构角度）用一个经济的方法处理，改成了由钢纤维高强混凝土（SFHSC）和标准强度混凝土（NSC）组成的预应力梁。

从表中可以得到一些结论

·钢纤维（SF）对梁的弹性变形不起作用；

·钢纤维（SF）使截面极限应变增加大约2倍，对受弯构件产生附加塑性耗能的潜力

·相比于高强混凝土构件，在截面受拉层的标准强度混凝土（NSC）增加了约20%的截面塑性耗能潜力。

基于这些条件，作为截面延性的应变量，定量地计算钢纤维（SF）的含量是有可能的。

活动在截面上的纤维混凝土承受横向（泊松）拉应力，在这种情况下，钢纤维（SF）的作用是取代传统的钢筋。为了提供足够的延性，如果混凝土模块开裂，为了保证纤维能承受拉应力，就需要满足最小纤维含量。根据这个方法，最小纤维体积比minρf定义如下：

其中minρf是最小钢纤维体积率，%和Wallow受裂缝计算限制。这个计算建立在“应力—裂缝宽度”的关系的基础上，或者说是建立在“应力—应变”的关系的基础上的。相应的最小钢纤维（SF）体积率的值是根据表2确定的。

5、 截面延性应变量—钢纤维（SF）体积率的计算

在普通钢筋混凝土（RC）构件中，为了追求最小钢纤维（SF）体积率，设计计算就有必要了。这个设计的主要原则是：

—通过分析实验研究的结果，可以得出，处于受压区弯曲预应力截面的钢纤维（SF）在混凝土模块的变形量达到εC2后增加塑性变形量εCf。（见下图3）；

—额外的塑性变形量εCf应被认为是所需截面延性μreq的应变量，反过来作为一个设计参数给出；

—附加塑性变形的总变形量（考虑到纤维作用的局限性）应当小于或等于没有纤维的塑性变形量：

—钢纤维（SF）体积率假定是所需截面延性的线性应变量

公式（5）限制了附加塑性变形量εCf的最大值。限制它的最小值也很重要。根据公式（14），它应当符合最小钢纤维（SF）体积率minρf。如上所述，按最小钢纤维（SF）体积率的定义，如果在混凝土模块中出现裂缝，纤维能够承受横向拉应变。在这种情况下

其中ν=0.2是混凝土的泊松系数。

可以得到钢纤维（SF）增加的附加延性△μ为：

其中

考虑到纤维作用的局限性，根据公式（15），最大附加延性为：

必需的延性的最大值（根据公式（17））为：

其中Uctot和Ucel的含义分别见公式（9）和公式（6）

Uctot是通过标准抛物线函数的指数相当于n表述的变量

根据下面给出的两条限制条件，函数ρf=f（μreq）：

根据上面的这些条件，钢纤维（SF）体积率能够用所需延性的应变量μreq表述：

接近线性函数的ρf（μreq）可以根据下式计算：

ρf一μreq曲线见图4

6、 数例

为了证明提出的设计方法，来分析受压区添了纤维的高强混凝土（HSC）预应力量。受压区梁截面的高强混凝土（HSC）等级是90，根据欧拉规则，它的（见表2）， εc2=0.0026， ν=0.2，fctm=5Mpa,     εctul=0.12×10-3。对于给定的梁它的钢纤维（SF）体积率ρf可以根据所需的延性参数μreq=2μHSC计算。

根据公式（16），纤维提供的最小塑性变形量是

根据公式（10）可以得到受压区梁截面的延性参数如下：

=98×0.0026×〔1.4/（1+1.4）〕/（0.5×0.0023×98）=1.36

双层量

=1.36×1.2=1.64

然后，根据给出的设计材料，所需的延性参数等于

μreq=2μHSC=2×1.64=3.28

根据公式（20），允许必需延性的最大值为

即延性参数的计算值小于允许最大值。

（根据公式（12））最小钢纤维（SF）体积率为

根据公式（20），所需延性的最小值为

=（2×0.6/2.23）+1.64=2.18

根据公式（23）钢纤维（SF）体积率的设计值为

应该提及的是在大多数实验研究中钢纤维（SF）体积率ρf≤2.5%。

根据公式（23）μreqmax代替μreq就能相应地得到ρf的最大值

设计值ρf=4.0%属于ρfmin=2%到ρfmax=8.63%的范围，满足条件ρfmin≤ρf≤ρfmax

7、 结果与讨论

在受弯预应力构件中，用由在受弯截面用高强混凝土（HSC），在受拉截面用标准混凝土（NSC）构成的双层梁是有效的。众所周知，预应力钢筋束的出现大大提高了截面的延性，因为钢筋束的高强钢筋存在脆性性能，即应力—应变曲线图中没有屈服点。

高强混凝土（HSC）也能使用钢纤维（SF），这能改善受压梁的塑性能力。而且，增加钢纤维（SF）大大改善了混凝土模块与预应力钢筋的粘结。它能更好地促进混凝土和钢筋混凝土的共同作用，这对结构形式很重要。

钢纤维（SF）的另一项重要作用是缩短了先张法构件的传递长度。顺着梁的两端它能承受更多的预应力均布荷载，同时提高了构件的利用率，换句话说，由在受弯截面用高强混凝土（HSC），在受拉截面用标准混凝土（NSC）构成的双层梁成了高性能构件。

预应力双层钢纤维（SF）梁的设计对钢筋混凝土（RC）结构造成了一系列新问题。它包括了一些创新的子问题，像高强混凝土（HSC）等级的定义，最小最大钢纤维（SF）体积率的获得，作为预应力截面延性应变量的钢纤维（SF）体积率的计算等等。作者在前面已经给出了高强混凝土（HSC）的定义。

在这篇文章中，对双层预应力梁的最低高强混凝土（HSC）等级的计算方法已经提出来了。在受压区有高强混凝土（HSC）的双层梁在弯曲时具有较高的开裂承载力。使用根据上述方法选择的高强混凝土（HSC）等级能制止对受压区截面预应力钢筋束使用的必要性。

很明显，由受压区的高强混凝土（HSC）和受拉区的标准混凝土（NSC）组成的双层截面的延性参数是很小的，它的值接近于1.0，即受弯构件截面是脆性的。它限制了这类结构在地基及其它动力荷载作用区运用的可能性。因此使用钢纤维（SF）的附加原因是为了在受压截面获得高性能混凝土（HPC），当然因为在受拉区混凝土的作用是可以被忽略的，所以在受拉截面区没有必要使用高性能混凝土（HPC），当然标准强度混凝土（NSC）也没必要增添纤维。仅在受压区使用高性能混凝土（HPC）就能达到钢筋混凝土（RC）截面必须的延性。

对各个等级的高强混凝土（HSC），最小钢纤维（SF）体积率是不同的，为许多研究人员所用的0.5%到2.5%范围的钢纤维（SF）体积率是很接近于最小钢纤维（SF）体积率的。这些比例符合了混凝土横向（泊松比）拉应变，但它们并不能完全保证截面的延性。钢纤维（SF）体积率的真实值应是必须延性的应变量，反过来说，应是一个设计参数。而且，考虑纤维的作用，在梁中附加的最大塑性变形量不能超出没纤维梁的塑性变形量。根据这些规则，“钢纤维（SF）体积率—所需延性”函数被确认接近于线性。这样根据所需截面延性就能计算钢纤维（SF）体积率了。

8、 结论

对由受压区的钢纤维高强混凝土（HSC）和受拉区的标准强度混凝土（NSC）组成的双层弯曲预应力梁的设计方法被提出来了。很明显，对双层弯曲构件计算纤维体积率是很重要的，就跟对普通钢筋混凝土（RC）计算钢筋含量一样重要。实验结果表明，在这种情况下，由钢纤维高强混凝土（HSC）和标准强度混凝土（NSC）构成的双层构件成了高性能混凝土（HPC）。

对给定标准强度混凝土（NSC）等级的受压区双层预应力梁，确定高强混凝土（HSC）最低限制的强度等级的方法被提出来了。实验结果表明，钢纤维（SF）对梁的弹性变形几乎不起作用，但是，由于钢纤维（SF）的塑性耗能潜力，梁的极限变形量增加了。

相比于单层高强混凝土（HSC）量，在受拉截面使用标准强度混凝土（NSC）又增加了20%的截面塑性耗能潜力。

基于在混凝土模块中钢纤维、能够在产生裂缝时承受拉应力的事实，作为所需延性应变量的钢纤维（SF）体积率的计算设计方法被提出来了。说明这个方法的有效性的数例，表明用于先前的由其他研究人员开展的实验工作的钢纤维（SF）体积率只要符合纤维的最低含量的需要即可。

在这篇文章中，为定量地定义双层梁钢纤维（SF）体积率的理论背景包括了所需截面的延性参数，并且为新设计技术运用奠定了基础，它也进一步推动了高性能混凝土（HPC）结构的实验研究。