摘要：

本文是两篇配套论文的第二篇，旨在探讨钢筋混凝土框架结构在地震中的抗倒塌安全性，并检验加利福尼亚州在20世纪70年代中期之前所建非延性框架结构建筑的可靠性。基于对结构响应的非线性动态模拟进行概率评估，以此来计算对应于不同的地运动特性和结构类型时结构倒塌的危险。评估的对象是一套不同高度的非延性钢筋混凝土框架结构原型，它们是根据1967年版《统一建筑规范》中的抗震规定设计的。结果表明，当处于一个典型的加利福尼亚高震场地时，非延性钢筋混凝土框架结构发生倒塌的年平均频率范围为（5～14）×10-3，这比按现代规范设计的结果高出约40倍。这些数据表明新规范对延性构造和能力设计要求是行之有效的，这使得在过去的30年中新建的钢筋混凝土建筑物的安全性得到明显改善。通过对延性和非延性结构的安全性比较，有助于出台新的规章来评估和减轻现有的钢筋混凝土框架结构建筑物地震倒塌的危险。

关键词：倒塌；地震工程；结构可靠度；钢筋混凝土结构；建筑；商业；地震影响。

引言

20世纪70年代中期以前加利福尼亚州建设的钢筋混凝土框架结构缺乏好的抗震设计理念（例如：加强柱子、钢筋延性构造），这使得它们很容易在地震中发生倒塌。 这些非延性钢筋混凝土框架结构在经历了加利福尼亚州1971年圣费尔南多大地震，1979年英皮里尔谷大地震，1987年惠蒂尔纳罗斯大地震，1994年北山大地震和世界上其他地方发生的无数地震之后，已经遭受了很严重的地震损害。这些因素促使人们关注加利福尼亚州的近40000栋钢筋混凝土建筑，其中的一部分在未来地震中可能会发生倒塌而危害生命财产安全。然而，我们缺乏足够的数据来衡量建筑的危险程度，因而无法确定是大量的建筑均存在这种危险，还是只有特定的建筑物才存在危险。一栋建筑物发生倒塌的危险大小，不仅取决于其原设计采用的建筑规范中的规定，也取决于结构布置、施工质量、建筑位置和场地的地震特性。除了需要准确评估倒塌的风险之外，选择合适的危险承受值和最低的安全标准也是需要考虑的问题。在这方面，通过比较评估根据新老建筑规范设计出的建筑物，能帮我们找到一种评估手段来确定目前设计能够接受的风险水平。

20世纪70年代中期以来，随着对地震破坏和钢筋延性的深入了解，建筑规范中对于钢筋混凝土抗震设计和构造措施的要求发生了显著变化。同老式非延性钢筋混凝土框架结构相比，现代规范要求在高地震地区的框架结构要进行各种能力设计来防止或延缓不利的破坏形式（如柱剪切破坏，梁柱节点破坏）。虽然人们普遍同意对于建筑规范的这些修改是适当的，但还是缺少足够的数据以量化其对地震安全性的改善程度。这项研究采用基于性能的地震工程方法，以评估地震引起非延性钢筋混凝土框架结构倒塌的可能性。基于性能的地震工程提供了一个概率框架，利用非线性时程模拟将地面运动强度与结构响应和建筑性能联系起来。对非延性钢筋混凝土框架结构的评估基于原型结构所做的测试，这套结构是根据1967年《统一建筑规范》设计的。这些原型结构代表了1950年至1975年间在加州建造的普通钢筋混凝土框架结构。通过对非延性混凝土框架结构原型的非线性动态分析可以预测倒塌的发生，而在结构倒塌过程中利用仿真模型能够捕获强度和刚度的变化特征。抗倒塌性能评估的成果是一系列保障建筑安全的措施，并将地震中抗倒塌能力与地震灾害联系到一起。我们将这些结果与另一篇配套论文中的关于延性钢筋混凝土框架结构的数据进行比较。

原型钢筋混凝土框架结构

这些非延性钢筋混凝土框架结构原型考虑了结构高度的变化，结构布置和细部设计，能够覆盖加州旧钢筋混凝土框架结构建筑物设计和性能的的预期范围。制作原型时，我们查阅了钢筋混凝土部件和框架的关键参数，这些参数是由哈兹尔顿等人通过分析和实验获得的。本项研究共制作了26个非延性钢筋混凝土框架原型建筑物。 本文主要侧重于这些设计中的12个，高度从2层到12层变化，并包括具有可替换设计细节的周边和空间框架侧向抵抗系统。原型建筑均设计为有着20厘米平面楼板系统和7.6米柱间距的办公楼房。2层和4层建筑的平面尺寸为38.1m×53.3m，8层和12层建筑的平面尺寸为38.1m×38.1m。建筑首层层高4.6m，其余层层高4.0m。我们参考了20世纪60年代在加州建设的钢混建筑的原结构图，来为原型结构选择典型的结构部置和几何形状。原型仅限于无填充墙的钢筋混凝土框架，并且在高度和平面上比较规则，没有出现明显的强度或刚度突变。

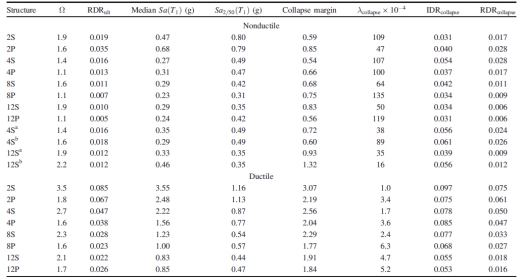
非延性钢混原型结构是按照1967年《统一建筑规范》中的最高地震烈度区（3区）设计的，那个时代加州的大部分都属于这个烈度区。二维框架的结构设计是由所需的强度和刚度控制的，应满足重力和地震荷载组合的要求。设计也符合所有相关的建筑规范要求，包括最大和最小配筋率和最大箍筋间距。1967年《统一建筑规范》规定，如果采用了延性构造措施，可以适当地减小基底剪应力。然而，本研究并没有进行这种折减，只考虑标准的细部构造。表1总结了每个结构的设计细节，在Liel 和Deierlein处可以获得非延性钢混原型的完整资料。有4个4层和12层的原型做了细部加强，这会在随后的文章里作介绍。

我们将非延性原型钢混框架结构的抗倒塌性能与配套论文中的延性原型钢混结构做了对比。如表2总结，这些延性框架的设计依据了《国际建筑规范》（ICC  2003）、ASCE 7 (ASCE 2002),、和 ACI 318 (ACI 2005)中的规定，并符合所有相关规范中关于强度，刚度，承载能力和特殊框架构造的要求。这些结构得益于自20世纪70年代以来钢筋混凝土抗震设计规范不断增加的条款，包括各种关于能力设计的规定（例如：强柱弱梁，节点抗剪承载力设计）和构造措施的改进（例如，在梁柱塑性铰区增加横向约束，提高对搭接的要求，闭合箍筋）。这套延性钢混框架是按照在土壤类型为Sd类的典型高震洛杉矶场地设计的，它处在2003版IBC设计地图的过渡区域。

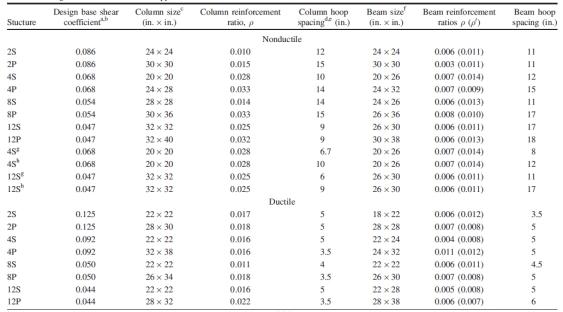
表1  原型延性和非延性框架的设计属性

附注：

a) 1967年《统一建筑规范》（UBC）中设计基底剪切系数取值为C=0.05/T（1/3）≤0.10。对于抵抗力矩的框架T=0.1N，N是层数（ICBO 1967）；

b) 现代建筑的设计基底系数根据设计场地的反应谱取值。洛杉矶场地的设计反应谱SDS=1.0g，SD1=0.60g。计算式采用的周期根据规范公式算得，是结构的高度（英尺），并且规定了计算周期的上限（）(ASCE 2002)；

c) 柱子的属性沿结构高度变化，此处列出的是首层柱子的属性；

d) 各构件横向钢筋的配置由所需的剪切强度确定。每个位置至少有两根3号钢筋；

e) 延性钢筋混凝土框架横向钢筋的配置由所需的剪切强度确定。所有的弯锚都有抗震构造，并使用4号钢筋(ACI 2005)；

f) 梁属性沿结构的高度变化，此处列出的是第二层梁的属性；

g) 所设计结构的梁柱构造优于平均水平；

h) 所设计结构的节点构造由于平均水平。

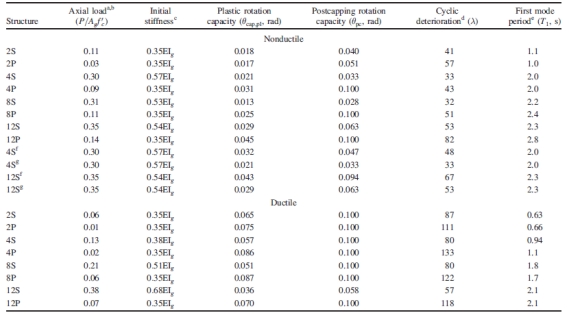
表2  原型延性和非延性框架的建模参数

附注：

a) 此处列出的是首层柱的参数；

b) 轴向荷载包括恒荷载和25%的活荷载；

c) 有效割线刚度为通过40%屈服强度时的割线刚度；

d) 滞后能量耗散的计算公式为；

e) 参数获得于对结构模型的特征值分析；

f) 所设计结构梁柱的构造优于平均水平；

g) 所设计结构的节点构造优于平均水平。

对比表1所示的结构，我们可以看出在过去四十年间钢筋混凝土框架抗震设计规范的变化。尽管对设计基底剪力的方程进行了修改，但对于相同高度的延性和非延性钢混框架结构，计算的结果还是相当接近的，只有在计算最矮的结构时才有较大的偏差。两组建筑物之间明显的差别是部件的设计和构造措施，特别是在数量、布局、和横向加固方面。现代钢混框架结构受剪切能力设计规定的影响，对于箍筋间距有着更严格的限制，例如：在延性钢筋混凝土梁和柱中横向钢筋要加密2到4倍。最小配箍率保证了柱子有足够的强度来延缓楼层机构的形成。因此，在节点处柱强度与梁强度的比值延性钢筋混凝土框架结构平均比非延性钢筋混凝土框架结构高出约30％。非延性钢混框架结构对于梁柱节点区域的设计或加固也没有特别规定，而延性钢混框架结构的柱子则要求规定的尺寸并添加横向钢筋，以满足节点剪力的需要。为满足特殊框架结构对节点剪切强度的要求，通常增加柱子的尺寸，从而减小轴压比。

非线性仿真模型

每个原型非延性钢混框架的非线性分析模型，都包括一个二维三开间的侧向抗力系统，如图1所示。分析模型能够体现柱子、梁、梁柱节点材料的非线性和大尺寸效应（P-Δ效应），这对于模拟框架的倒塌时十分重要的。我们用端部部分铰接的构件模拟梁、柱及其节点，这些铰被部分约束以模拟真实情况，类似于弹簧铰。  结构模型不包括任何非结构构件或支撑重力荷载的部件，它们都不属于横向支撑系统。本模型是在OpenSees中建造的，该软件具有强大的计算功能。

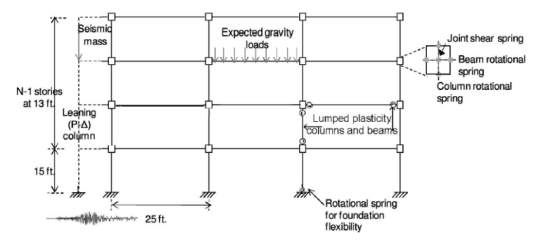
图 1. 钢筋混凝土框架结构分析模型示意图

在另一篇配套论文中，用集中弹簧模拟非弹性的梁、柱、节点，它们是根据三线图和伊瓦拉等人的滞后原则理想化而来的。根据一系列经验关系，我们对代表梁和柱构件的非线性弹簧特性进行了预测，这些关系将柱子的设计特征同建模参数联系起来，并与实验数据进行了校核。用于改进经验关系的试验，包括大量非延性构造的钢筋混凝土柱。预测的模型参数反映非延性和延性钢筋混凝土构件的弯矩-转角行为的差异。正如配套论文中所说的，由于缺少足够的梁的数据，对于钢筋混凝土梁的模型参数的校核是建立在柱子在低轴压水平下被测试的基础上的。图2（a）显示了延性及非延性柱（均为4层建筑）的单调骨干曲线的性质。众所周知，最大塑性转角θcap,pl对预测倒塌的发生有重要影响，它是柱子约束钢筋和轴压水平的函数，延性钢筋混凝土柱比非延性钢筋混凝土柱大约大2.7倍。延性钢筋混凝土柱还有更强的后期旋转能力（θpc），这决定了的柱子屈服后强度退化的速度。图2(b)表明在一个典型的地震加载过程中，柱的强度和刚度不断下降。起始曲线的减弱过程由弱化参数λ控制，这是一个耗能的过程。在非延性柱中由于缺少足够的约束，并且轴压荷载更大，其耗能的能力要比延性柱小很多。模型参数需要校准到预期的水平。在分析时需计入重力荷载，并忽略轴向、弯曲、剪切变形之间的相互作用，而这些因素对高层建筑物的影响是十分明显的。

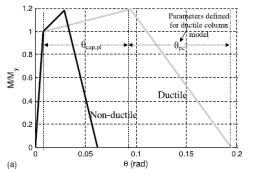
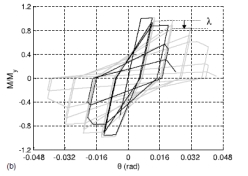
图 2. 用非弹性弹簧模拟位于4层框架结构首层中的钢筋混凝土柱

，其特点是：（a）单调；（b）循环。

表2中为非延性和延性的原型钢筋混凝土柱的建模参数。钢筋混凝土梁的属性也是类似的，它们在其他地方被列出。所有模型元件的属性值都取为为测试值的中值尽管原型梁和柱的建模参数已经考虑了构件端部的粘结滑移，但它们还是不能模拟到由于非延性框架锚固或搭接失效而引起的显著破坏。

同延性框架设计时限制节点剪切变形不同，非延性框架可能会有明显的剪切变形而加快倒塌过程。如图1所示，用非弹性弹簧来模拟节点的剪切行为，模型需遵循单调曲线和滞后原则（与图2中柱的图形类似）。参考了仅有极少横向钢筋的节点的数据，并结合了其他非延性特性，我们为节点剪切弹簧赋予了属性。不幸的是， 可获取的不合格节点的数据是十分有限的。

节点剪切强度使用ACI318公式的改进版本进行计算，大小取决于节点尺寸（bj是节点宽度，h是节点高度）、混凝土抗压强度（fc′，单位：psi），约束系数（γ，取值为12～20），公式为：V = 0.7γ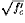bjh 。根据米特拉和罗斯的实验数据，我们引进了0.7的修正系数。修正系数反映了具有抗震构造的节点与没有横向钢筋的节点剪切强度的差异。我们假定约束钢筋混凝土节点呈线弹性变化，但非延性钢筋筋混凝土却只有有限的塑性，其内外节点的最大塑性剪切变形分别为0.015和0.010。根据Pantelides等人的研究数据，轴压比低于0.095的节点可近似看做变形呈线性变化（至 0轴轴向荷载最大值的0.025）。现有数据表明，有效初始刚度大约会下降10%。由于缺少足够的数据，我们假设钢筋混凝土梁柱的削弱特性是相同的。

表2为计算所得的钢筋混凝土框架的弹性基本周期，它反映了梁柱的开裂刚度（梁：0.35 EIg；柱：0.35～0.80 EIg）、节点尺寸和面板柔度。构件的有效刚度对应于达到屈服强度的40%时的变形 ，并包括构件端部的粘结滑移。由于建模时采用的假定不同（有效刚度的取值差异和不考虑重力支撑系统），并且计算结构周期的公式偏于保守，所以计算出的周期会明显大于按其他简化公式的计算结果。

分析模型的非线性静态分析结果表明：现代的钢筋混凝土框架结构比老式的非延性框架结构更坚固，而且有更强的变形能力，从图3中我们可以清楚地看到对比的结果。分析时荷载采用ASCE 7-05等效地震荷载分布。横向强度的高低根据安全系数来比较，安全系数是极限强度同设计强度的比值。延性的好坏是根据最大层间位移角来判断的，即当结构丧失20%横向强度时的层间位移角。正如表3所示，延性钢筋混凝土框架与非延性框架相比，安全系数大约高40%，最大层间位移角大3倍。导致延性框架有更强的结构变形能力和更多的安全储备的原因是：（1）延性构件的变形能力更强；（2）延性框架发生的屈服更多；（3）框架柱的强度更大；（4）梁的屈服耗能更多。图3（b）表明地震对于建筑低层的破坏更严重，在非延性结构中这种现象更为突出。然而非线性静态分析的方法并不是对动态分析的简单叠加，实验结果有助于找到动态分析结果的规律，从而总结出非线性静态评估的方案。

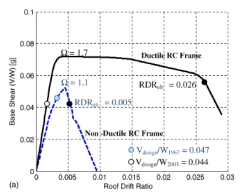
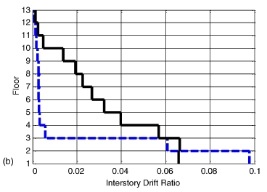
图 3.  12层延性与非延性钢筋混凝土框架分析图：

（a）内力-位移响应；（b）最终楼层位移分布。

抗倒塌性能评估步骤

对非延性钢筋混凝土原型框架的抗倒塌性能的评估与对延性框架的评估方法相同。用非线性仿真模型的增量动态分析（IDA）来评估抗倒塌性能，通过增大振幅来模拟结构所处的不同地运动。对于每种地运动，当出现过大的层间位移时，我们就认为结构失效。分析过程中，我们对 80种不同的地震记录进行了测试。评估的结果显示，结构倒塌的可能性与地震强度呈对数正态分布关系（中位数、标准差），这可以整理为一个计算结构倒塌危险性的函数。但对于地震的记录不是那么可靠的，这与地震频谱的不断变化和地震记录的特点有关。

尽管钢筋混凝土框架结构的非线性分析模型可以模拟出由梁柱强度、刚度丧失或梁柱节点剪切变形所引起的倒塌，但却不能直接模拟柱子的剪切破坏。我们期望在测试过程中柱子先屈服后剪切破坏，而不是像非延性短柱那样直接发生剪切破坏。可观测的地震破坏和实验研究表明柱子剪切破化和重力支撑系统的损坏会导致非延性框架连续倒塌。由于难以准确地模拟剪切、弯剪破坏和轴向受荷能力的丧失，所以不能直接模拟出柱子的剪切破坏。

对构件极限状态的后期动态分析，可以检测出与柱子剪切破坏有关的倒塌模式。从非延性梁柱的实验数据中可以推导出构件的极限状态函数，用这个函数可以预测当发生剪切破坏和垂直受荷能力丧失时，柱子的平均位移比（CDR）。这里所说的CDR与层间位移角类似，因为这个函数是建立在柱构件的实验数据的基础上的，所以不包括梁旋转和节点变形对位移的贡献。

当柱子发生弯剪破坏时，构件间的关系我们直接采用已有的研究成果。对于本研究中未进行延性设计构造和轴压比P/Agfc′在0.03到0.35之间的柱子，Aslani 和 Miranda预测当CDR在为0.017～0.032rad时，柱子就会发生剪切变形，当然这还与柱子的性质和轴压下变形能力下降的程度有关。当CDR为0.32～0.10rad时，柱子的垂直承载能力就会不断丧失，当然这也与柱子的属性有关。

由于柱子竖向承载能力的丧失会导致结构倒塌，所以我们将这种破坏状态也归类于结构倒塌破坏在分析过程中，任何一根柱子的位移超过了按函数计算出的容许值，结构都会进入竖向倒塌临界状态。如果在较小强度的地震中，结构更容易发生竖向倒塌，而不是侧向倒塌，那么对于倒塌的统计结果就需要更新。柱位移的概率分布是地震强度与构建性能的函数，可以用这种简化方法将其积分为一个可比较的数值结果。我们假定对于只有侧向位移的情况和既有侧向位移又有轴向削弱的情况，其倒塌的不确定性是相同的，这是因为它主要是由建模和记录的不确定性确定的，而不是由构件性能的不确定性。

考虑垂直倒塌极限状态会降低结构预期的抗倒塌能力。图4是8层钢筋混凝土框架结构的倒塌概率曲线，分别对应于计入和不计入剪切破坏和由剪切引起的轴向失效的情况。如图所示，如果考虑柱子的剪切破坏，倒塌的可能性就会比侧移模式大大降低。然而，如果我们假设柱子的剪切失效不会直接导致倒塌，而是柱子轴向承压能力的丧失导致的倒塌，那么这样的结果只会比只考虑侧移的计算结果稍小一点。对本文所研究的非延性钢筋混凝土框架而言，极限状态计入竖向承载力的损失比不计入这种损失的统计结果平均小2%～30%。

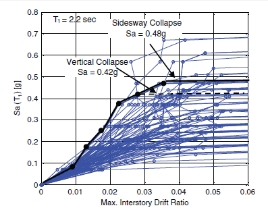
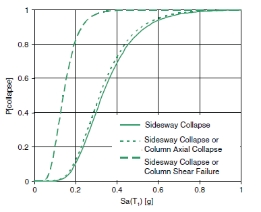
图 4.   8层框架结构的IDA结果分析：

（a）增量动态分析时，对于选定的地震，竖向失效模式对抗倒塌能力的影响；

（b）只有侧移失效时的倒塌概率与既有侧移又有竖向失效的倒塌概率对比。

记录变化的计算值为0.35到0.45之间。非线性模拟模型究竟能有多符合实际建筑是不确定的，这就是所谓的建模不确定性，我们通过增加结构倒塌概率的离散度来考虑这种不确定性。Liel等人以前就证明过在评估地震倒塌危险时考虑建模的不确定性是十分重要的，这是因为构件的变形能力、结构的后续变化和建筑倒塌时的明显的非线性都很大的潜在不确定性。总的不确定性的平方等于记录不确定性的平方与建模不确定性平方之和：σln⁡,Total2 = σln⁡,RTR2+σln⁡,Modeling2 。这种简化的方法提供了对倒塌概率合理的估计方法和年平均倒塌频率。假定建模误差σln⁡,Modeling = 0.50，则对于原型非延性框架结构总误差范围σln⁡,Total = 0.61～0.67。

正如Haselton等人所述，失效概率函数的参数还需要调整以考虑加利福尼亚罕遇地震与一般地震谱型的差异。一般情况下，这种调整会使非延性钢筋混凝土框架结构的抗倒塌能力增加25%，而延性混凝土框架结构会提高60%。造成这种差异的原因有：（1）非延性框架在倒塌前经历的周期范围更窄，这对于谱型发挥有利影响是必需的；（2）非延性框架倾向于在加速度频谱较小的位置发生倒塌，这个位置对应的地震比较频繁。 有兴趣的读者可以参考Haselton等人对于该步骤的详细描述。随后会讨论原型建筑最终的倒塌概率曲线，包含了建模不确定性和谱型调整。

评价抗地震倒塌性能的关键指标包括：抗倒塌能力的中值、倒塌安全保证率和倒塌的年平均频率。根据地震强度Sa(T1) (g)我们可以给出抗倒塌能力的中值，大小主要取决于原型的自振周期。用倒塌安全保证率可以更容易地比较结构的抗倒塌性能，它是在50年范围内超越概率为2%的地震强度Sa2/50(T1)下，结构抗倒塌性能的中值。Sa2/50作为标准参数，是确定大多数场地需考虑的最大地震强度的依据。第三个指标是倒塌的年平均频率(λcollapse)，它是通过将倒塌概率函数与特定场地的危险曲线整合后获得的 。危险曲线代表了在一个选定的场地发生超过某个特定强度的地震的可能性。出于研究目的的考虑，危险曲线定义为在一个洛杉矶盆地的高震场地，其不受近场方向性的影响，而且一般代表高震区域。对特定场地的地震危险性分析将会改变在其他加利福尼亚场地的做出的评估，但对于所有处在1967版《统一建筑规范》的第3区的场地，其原型建筑的设计是相同的。

地震倒塌评估的结果

表2  原型延性和非延性框架的建模参数

附注：

a) 所设计结构梁柱的构造优于平均水平；

b) 所设计结构的节点构造优于平均水平。

所有原型钢筋混凝土框架的抗倒塌性能的评估结果在表3中被列出。倒塌评估考虑了侧移倒塌（模拟）和垂直失效（未模拟）两种模式，并且包含了结构建模的不确定性。相应的倒塌危险曲线如图5 所示，为了方便对比，每座原型建筑的水平轴向地震强度都利用Sa2/50(T1)进行了标准化。倒塌的年平均频率如图6所示。除了特定地震强度下的倒塌性能外，表中也列出了楼顶位移比(RDRcollapse)和层间位移比(IDRcollapse)。这些位移是在结构侧移倒塌之前的最大地震强度下记录的。

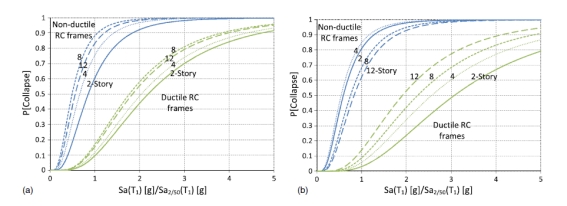
图 5. 倒塌危险曲线：

（a）原型钢筋混凝土四周框架；（b）原型钢筋混凝土空间框架

.

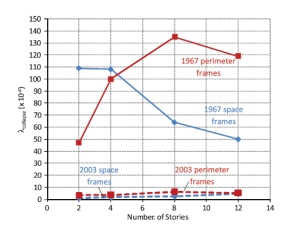
图 6. 原型非延性和延性框架倒塌危险评估的对比（倒塌的年平均频率）

非延性和延性钢筋混凝土框架评估的对比

如表3所总结的，分析结果表明非延性钢筋混凝土框架的倒塌安全储备从0.54到0.85，这表明倒塌时强度中值比Sa2/50(T1)强度小。形成对比的是，延性钢筋混凝土框架的倒塌安全储备率几乎大三倍，从1.77到3.07。非延性钢筋混凝土框架建筑已经计算出了倒塌的年平均频率为47～135×10-4，相当于处在加利福尼亚高震场地的建筑物在50年间发生倒塌的概率为21%～50%。对于延性钢筋混凝土框架建筑，倒塌的年平均频率为1～6×10-4，相当于在50年间发生倒塌的概率为0.5%～2.9%。一般来说，空间框架比四周框架的倒塌安全储备要更大，这主要是因为空间框架设计时附属重力荷载更明显，有更多的强度富余。

倒塌的年平均频率在图6中做了进一步的对比，它说明了延性（2003）与非延性（1967）框架建筑倒塌危险的巨大区别。非延性四周框架与延性四周框架相比，发生倒塌的可能性大约大了20倍。非延性空间框架与延性空间框架相比，发生倒塌的可能性大了60倍。图6还表明即使对于每套建筑倒塌的危险性也有十分明显的变化，例如2层和8层的非延性空间框架危险指标相差了大约3倍。为了验证造成倒塌指标差异的可能原因，我们在图7中将倒塌的年平均频率与静态强度富余关系绘出。无论是延性还是非延性框架，倒塌的年平均频率都是随着静态强度富余的减少而增加的，但这个关系在非延性框架中不明显，年平均频率的变化远大于延性框架。由于数据量比较少，变化反映了每个原型设计的独特性，虽然非延性框架有较大的离散性，我们仍可以从这些对比中得到可靠的结论，随后的部分将会对非延性框架行为的差异做出更深入的讨论。总的来说，从1967的设计到2003的设计中预期抗倒塌能力、延性、一致性的改善反映了近几十年钢筋混凝土规范中对于抗震总体设计和构造措施的改变。

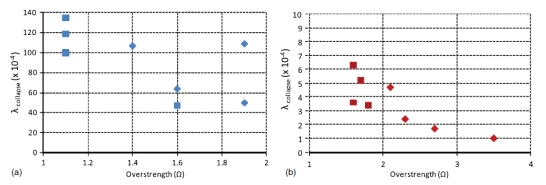
图 7. 静态超强值与倒塌的年平均频率之间的关系（菱形标志为空间框架）：

（a）非延性钢筋混凝土框架；（b）延性钢筋混凝土框架。

抗倒塌性能评估从更深层次反映了倒塌行为与结构整体延性间的关系。参照表3，延性框架在倒塌前的最大楼顶位移比(RDRcollapse)为1.6%～7.5%。这些值大约比非延性框架（RDRcollapse = 0.6% to 2.8%）大2.4倍相应的延性框架倒塌前的层间位移比非延性框架大1.8倍。造成这些不同的部分原因是构造措施的改进使构件变形能力的增加，如表2所示。1967年到 2003年设计中的RDRcollapse的增大也表明了现代建筑要求的强柱弱梁比有助于将破坏扩散到更大的范围，增加结构的能量耗散和改善体系的延性。图8中是8层和12层原型框架的倒塌模式对比。非延性框架建筑一般只在第一层和第二层发生破坏，然而现代延性框架会发生更分散的屈服和失效模式。

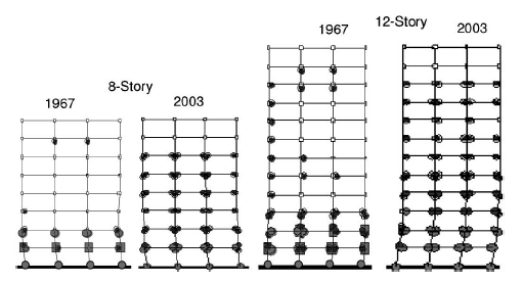
图 8. 原型空间框架预期的侧移倒塌模式简图

非延性钢筋混凝土框架抗倒塌性能的变化

这套原型非延性钢筋混凝土框架设计上的区别导致了预期抗倒塌性能的变化，代表了具有一般几何形状和设计特点的非延性钢筋混凝土框架性能的可能范围。四周框架结构和短的空间框架结构的抗倒塌性能最差。四周框架结构的抗倒塌安全性随着高度逐渐削弱，这是因为侧向荷载会随着建筑高度的增加逐渐成为设计的控制因素，而这会使侧向超强值降低。与此相反，在空间框架和较短的建筑的设计中重力荷载更为重要，间接提供了额外的侧向强度富余。因此，相对较小的基底抗剪承载力和刚度的累积效应使较高的四周框架对于P-Δ效应更敏感。空间框架比四周框架更有可能因为剪切破坏而引起重力承荷能力的损失，这种破坏模式未在被模拟。然而，本研究将四周框架与空间框架性能之间的区别放大了，这是因为四周框架体系的模拟模型忽略了重力体系构件（例如：无梁楼板和内部承重柱）对侧向强度和刚度的作用。Haselton等人发现在倒塌评估时考虑承重体系，会使4层现代框架结构的抗倒塌能力中值提高大约10%。

除了考虑建筑高度和框架体系的变化外，与典型结构相比有着较好构造措施的非延性框架结构也被认为是本研究的研究对象。到十九世纪六十年代，工程师们开始意识到抗震构造的重要性，在一些设计中，他们选择施加更多的横向钢筋，并加强了 梁、柱或节点处钢筋的锚固。这些理念被Blume等人在报告中提出，并在“加利福尼亚实践”中被实施。通过考虑两种设计的变体来检验采用更好构造措施的影响首先，假定柱子的箍筋在节点处连续（表1中4Sh 和 12Sh）。现代标准对节点处横向钢筋有着严格的规定，但在1967年的《统一建筑规范》中却没有相关确定。在非线性分析模型中，假定额外的节点横向钢筋会使节点抗剪强度提高20%。第二种设计变体假设梁柱箍筋间距缩小33%，这表示横向钢筋的使用量会增加50%。这种变化会增加钢筋混凝土构件的塑性和最大扭转能力，并减小循环强度和刚度退化，如表2所示。

对有着较好构造的原型结构评估的抗倒塌性能在表3中被列出，并与从4层和12层原型空间框架所获得的结果做比较。对于节点横向钢筋的规定只使4层框架的倒塌安全提高了11%，却使12层框架的倒塌安全提高了57%。之所以12层框架提高的更多，是因为节点强度的增强足以使损伤从节点转移到延性更好的梁和柱上。除了增加局部延性，这种变化还会使地震损伤延建筑高度更广泛地分布（表3中12S和12Sb RDRcollapse的增加表明了这种变化）。梁柱横向钢筋数量的增加导致了4层框架倒塌安全度增加了33%，12层框架倒塌安全度增加了12%。梁柱更好的构造通过增强构件变形能力和消除由于剪切破坏引起柱子倒塌的可能性，来达到增强抵抗侧移倒塌能力的目的。尽管如此，设计和构造分析的结果表明为使抗倒塌能力明显提高仍需进一步的改善。

结论

本研究评估处在地震区域的钢筋混凝土框架的抗倒塌性能的方法是设计、模拟和评估两套原型钢筋混凝土框架结构（现代延性框架和老式非延性框架）。原型框架高度变化从2层到12层，框架体系分为四周框架和空间框架。它们是按照1967年的《统一建筑规范》（UBC）和2003年的《国际建筑规范》（IBC）中的规定设计的，代表了各自时代具有抗震设计的框架结构。采用非线性模型来寻找因设计和构造特性而引起的性能上的区别。

正如预想的那样，对于任意高度和体系类型，延性框架（2003）都要明显优于非延性框架（1967）。现代框架结构能够经受住更大烈度的地震，在倒塌前会发生更明显的变形。延性框架的倒塌安全比比非延性框架大约大3倍。按照倒塌的年平均频率，在典型加利福尼亚高震场地的非延性框架倒塌的危险性是非延性框架的40倍。对现代延性建筑体系与既存非延性体系抗倒塌性能的对比评估为衡量易受地震影响的老旧建筑的安全性提供了依据。

在过去40年间钢筋混凝土框架抗震性能有了大幅度提升，这要归功于单个构件构造的改进（横向钢筋间距减小，封闭地震钩的使用，节点横向钢筋）和整体设计的要求（强柱弱梁比，其他能力设计要求）。现代钢筋混凝土框架梁、柱和节点的钢筋构造提高了构件的变形能力，减弱了随结构变形发生的强度和刚度的退化。能力设计防止剪切破坏和节点剪切变形的发生，并促进柱子屈服，使损伤和能量耗散沿着延性框架的高度更均匀地分布。这些构件和整体水平的改进导致了研究中倒塌安全结果的不同。

抗倒塌性能评估也用来证明对于非延性框架结构预期抗震性能的多变性。在这套规则的评估结构中，较高的四周型非延性框架结构最易发生侧移倒塌，这是因为他们的侧向超强值和柔度都比较小。空间框架的柱子承受了更大的轴向荷载，可能会发生柱子的剪切破坏和柱子承荷能力的损失，而导致结构较早地倒塌。本研究没有考虑高度不规则或设计施工有缺陷的结构，它们的抗震性能可能会更差。十九世纪六十年代加利福尼亚地区采用了一些构造措施在一定程度上改善了非延性钢筋混凝土框架的抗震性能，但与现代规范相比仍有较大差距。

在结果的推导，地震特性的描述，结构系列的识别和建立简化分析模型时我们都采用了各种各样的近似处理。尽管本研究进行了详细的分析，但仍有很多因素被忽略。例如，在四周框架中平面板重力体系提供的附加侧向抗力就没有被纳入模拟分析。此外，这些原型设计也没有考虑这些旧式建筑的设计师在规范的基础上对结构进行的加强。但与此相反，分析中也忽略了很多其他的破坏模式，如：搭接处的锚固破坏，柱子的倾覆，柱节点的冲剪破坏等。由于地震危害特点的不同，对于加利福尼亚不同的场地结论也会有所不同。抗倒塌性能评估结果的准确性是简化近似值的函数。结构建模和地震参数的巨大不确定性使本研究中对倒塌危险的测量值相对偏高。然而，倒塌能力参数的相对值和比较为地震安全提供了更重要的指标。

倒塌性能评估结果验证了预期的设想：非延性钢筋混凝土结构更易遭到破坏。结果还将现代延性结果与老式非延性结构安全性上的区别做了系统的量化处理。本研究所获得的非延性框架结构地震倒塌危险的参数可以被用于评估加利福尼亚地区的地震安全性。联邦政府已经出台了规定要求评估，改造或拆除无钢筋砌体结构。利用本研究的数据，并对改造或拆除进行成分效益评估，有助于评估有关消除非延性框架结构倒塌危险的政策的效果和确定最危险的建筑缺少对预期安全度和可接受危险程度的规定仍是政策的一个漏洞，我们可以通过本研究这样的基于性能的工程评估来弥补这个漏洞。

鸣谢

PEER中心通过国家自然基金的“地震工程研究中心计划”和应用技术委员会的“联邦紧急事务署P695 (ATC-63)计划”资助了本研究。此外，“斯坦福研究生奖学金”和“NSF研究生奖学金计划”也对本文作者进行了资助。作者感谢来自PEER，ATC和FEMA的合作者的参与及贡献，并鸣谢Jack Baker、 Brian Dean、 Charles Kircher、 Helmut Krawinkler、Eduardo Miranda、C. Marc Ramirez及三位匿名审稿人的建设性意见。