关于焊接滚轮架轴向窜动的实验研究

摘  要

文章引入焊接滚轮架轴向窜动的基本理论,并同时在焊接滚轮架的实验模型上进行了试验研究. 结果表明, 焊接滚轮架轴向窜动的主要原因在于工件的翻转存在着螺旋夹角. 轴向相对运动产生螺旋运动,弹性滑动与摩擦滑动. 其中有与理论相符的内容以及和理论不符合的内容,文中了轴向运动滚筒. 他是相对于轴运动的圆筒形工件. 相对轴的运动包括滚轮与工件相互协调的弹性滑动和摩擦滑动

关键词:焊接滚轮架; 圆筒工件; 滚轮; 轴向运动; 螺旋角

1 介绍

在焊接生产中,常会遇到旋转焊接圆形工件的情况。如焊接锅炉、石油化工压力容器等,就必须用到焊接滚轮架. 进行旋转焊接时，由于制造、装配公差 ，焊接滚轮和工件的表面平滑与否等因素(理想的旋转工件表面是平滑的)，使焊接不可能理想化的进行，工件必然会产生轴向窜动 。研究提供了当圆形工件焊接时，轴向窜动的机制. 这项研究成果将有利于研究与设计反窜动焊接滚轮架. 尤其是应用于滚轮架之上, 并确定了制造及滚轮架的装配公差 ，为通过机械调节的方式，避免轴向窜动的方法供理论依据。调整模式采用闭环控制电路,并推选有价值的提案

2理论分析

2.1焊接滚轮架一般由四个滚轮组成.由主动滚轮驱动,滚筒匀速绕轴旋转(例 1), 其间放圆形焊接工件（如图1）,其中,s 为滚轮支架距离,L同列两滚轮距离. Ve是圆形工件滚动的线速度,也被称为焊接速度

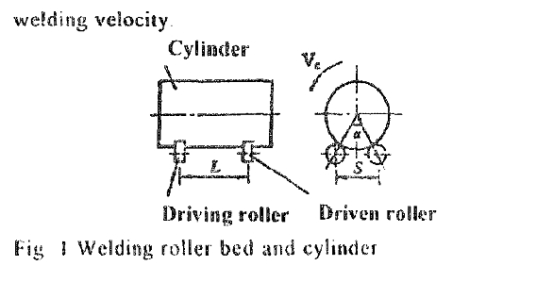
图1 焊接滚轮架

同行的滚轮的的轴并不平行, 从某个角度看,滚轮架的四辊所在的顶点组成一个简单的四边形 但如果四滚轮所在顶点不在同一平面 或因为制造及装配滚轮的圆柱是不规则的圆形. 那么. 工件就会在轴转动时窜动。滚轮架的滚轮与工件有一个接触点. 假设P为这个接触点. 工件的标准平面的定义是一个平滑的平面,平面A为圆柱母线与轴的切入点组成的平面,与工件相切点不在此平面内, 一平面垂直于平面A切线，过P和所在平面B 就是滚轮的切线过相同点P, 一般说来, θ被定义为滚轮轴和圆柱行工件的轴线的偏斜夹角! 定义螺旋夹角母线N和M'. 如图2、图3所示，其射影线取得的突出辊母线横跨点P 。 B定义为N和M线的投影夹角。如例3其中三个角度关系tanβ = tan2θ * tan 2γ  轴向偏差位移矢量和射影位移矢量它们的关系是:

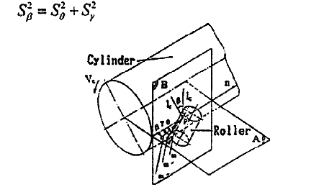
图 2滚轮和工件几何关系

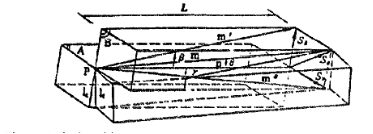
图3个角度矢量和位移矢量的关系

2.2轴向相对关系

(1)螺旋运动

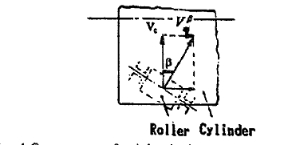
因为滚轮轴线与中线不平行, 在Vr和Vc之间就有一个螺旋角β存在,如图 2. 当辊筒围绕自己的轴线转动时,使在切线上产生摩擦力. 因为滚轮和工件各个线速度在不同的方向，由于螺旋效应也就是窜动就会发生在点p-滚轮和工件的接触点(图4).

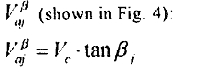
式中：VC是圆柱的线速.

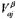是工件的轴向分量,

1.2.3.4, 分别代表四个滚轮.

(2)弹性滑动

由于存在一种螺旋角,在工件上产生轴向力Faj. 当力量小于最大轴向摩擦力fnj(其中f是摩擦系数,单滚和工件正常的压力) 工件会下滑超过滚轮轴 [2~3]mm

的下滑速度为.

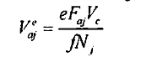
式中e是金属滚轮的弹性滑动系数：e= ool~~0.005.

(3)摩擦滑动时faj大于最高摩擦力fnj, 工件将在滚轮之上做摩擦滑动. 滑动阻力为fnj3. 工件的摩擦滑动速度的大小和方向可确定 由环球关系工件和四滚轮摩擦滑动导致滚轮表面的磨损. 这是意料之外的,在焊接进行时,工件发生漂移。以上三种运动不同时发生 。工件的轴向漂移速度不是代数的三个组成部分的速度.

whilst  in  the  case  of  frictional  sliding,  the  axial  velocity  is发生摩擦滑动的轴向速度

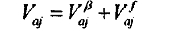
2.3工件滚轮的轴向运动

2.3.1与理论相符的部分

在理想的条件下, 工件和四滚轮之间的当螺旋角j都是一样时,即: 1=2=3=4工件的运动将与理论值相同. 可以将两个范畴对比分析:

(1)由于重力不存在轴向分量. 工件的轴向窜动速度:

Va=Vc * tanβ

(2)当存在一个有重力Ga因素，轴向窜动速度存在一个轴力. 现在,四滚轮有相同的方向

与重力G等效的轴向窜动速度 是：

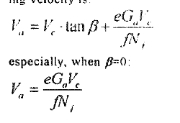
2.3.2.与理论不同的关于轴向窜动的内容.

工件与四滚轮之间螺旋角j大小和方向不相等.工件和四滚轮的几何关系也不相同时 ,工件和四滚轮之间的轴向窜动是个不相同的. 工件与滚轮轴向速度应该是同样的,因为工件被作为一个整视为一个刚体体,. 然而. 有些滚轮和工件的实际上轴向速度是不完全相同的, 所以轴向摩擦力几乎肯定会出现这种滚轮和工件之间以下两类分类讨论不同与理论的摩擦力的大小

(一)当轴向摩擦力确保每个滚轮和工件均低于最大轴向所需对摩擦力 滚轮和工件将产生弹性滑动单个滚轮和工件可以协调它们的弹性滑动

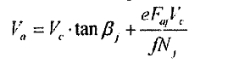
当工件的轴向速度是常量, 如果忽略重力工件与四个滚轮的轴向窜动的总和将为0

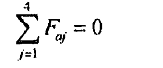
四个滚轮并没有什么差别因此他们大致是相同的

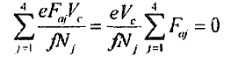
根据上述两个方程,工件的轴向窜动为：

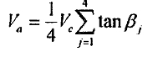
凡是0.25∑tant范围内.使用滚轮架的情况下,工件只长生产生弹性滑动,这可能是所谓工件 螺旋率螺旋问题

(2)当工件与滚轮的轴向摩擦力大于最大轴向摩擦力, 工件与滚轮的圆柱体之间将发生摩擦滑动,这滚那. 最大轴向力作用于滚轮轴承

Ffmax=fFNfmax

由于这种摩擦滑动的存在. 单个滚轮与工件之间轴向传动并不协调， 现在，轴向窜动并不完全由滚轮与工件的相对关系所决定. 很难写一个轴向传动速度的普遍相容方程,因为这样的条件 很复杂. 以下是进一步的分析和讨论这一问题时,首先,为便于分析问题, 螺旋角定义为

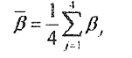
而相对螺旋角度

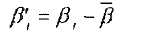
按由大到小的顺序排列β表达为

β1≥β2≥β3≥β4

同样的,滚轮与圆形工件的正常的相互作用力为n(j). 轴向力为

Fj≤fNj

一般 工件的轴向运动由螺旋角的平均值β决定

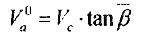
工件的轴向窜动,由相对螺旋角的定义窜动为不完全的组成部分, 当圆柱体沿着轴向，恒定速度 ，其速度表示分析表明asVa\n是平衡状态下的四滚轮轴力. 如果不考虑它的重力. 假设最大相对螺旋角对应工件的最大窜动速度为：

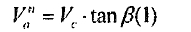
四个轴向力不可能相等

F1-(F2+F3+F4) ≤0

因为四个常力之间没有太大的区别, 四轴正常的力和摩擦所造成的窜动无疑高于其他三因素

否则,如果工件与滚轮之间螺旋角为最小相对螺旋β角时. 其速度. Va”  =  Vc * tanβ(4)

同样. 四轴向力无法平衡,即: [F(l)  + F(2)  + F(3) J  - F(4)  > 0因此,工件只能视为不兼容的轴向窜动的第二代或第三螺旋角,即:

If  N(I)  + N(2)  > N(3)  + N(4)

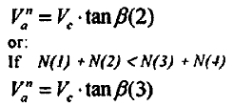
在上述意思的何种情况下. 有不完全平衡的轴向运动,有两个比较大的力滚轮驱动，另外两个较小的力阻碍滚轮的转动。即

f(1)+f(2)=f(3)+f(4)

根据上述分析,因为负荷而产生的不稳定的摩擦系数影响。材料，表面接触条件不完全的组成了轴向速度. 当工件作不完全的轴向运动时, 轴向速度是由一个协调因素va\0和一个非协调因素va\ni组成

Va=Va\0+Va\n

轴向窜动的最优化调整是为了使非协调因素尽可能协调和稳定从而减小小轴向窜动. 假设在某一特定滚轮架，轴向窜动的大小和方向是一定的.他对滚轮架将产生固定的影响 。

3. 实验

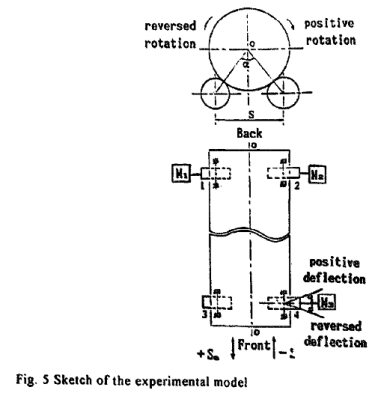
3.1.实验描述

在图5中试验表明,.初步的试验研究了两个因素:螺旋角和工件的线速度-影响轴向窜动的主要因素. 在实验过程. 轴向位移SA和轴向窜动速度va测量方法如例 5 。而进行的方法是将轴向位移传感器安装到的圆筒的一端.与传感器相连的X-Y记录器记录工件的轴向位移,每5s记录一次.,平均窜动速度va在每个角度可以计算出数据. 在试验阶段. 实验模型是如下:一.调节四滚轮 高度在同一用水平线上,

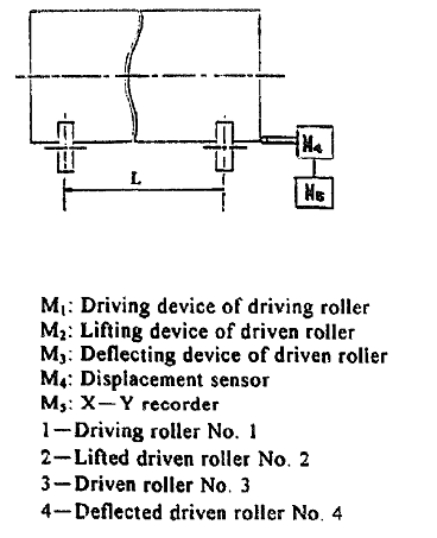
并在四矩形的个顶点.那么滚轮使旋转工件的相对平衡. 然后. 工件不窜动一段很长的时间. 或定期窜动一个很小的范围

3.2实验结果的讨论

3.2.1螺旋角的影响

(一)例如图六所示 。VA的变化检测条件是: vc=35m/h  L=422mm , α=60"

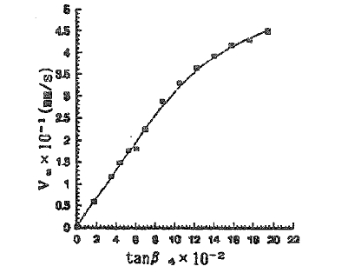
va是与tanβ4成正比的.β4 是与(1~~~6c )相关的.坡度线为3. 06毫米/秒,va不再正比tanβ4时, 当β4大于6c。轴向窜动是随着β4逐渐减小 。 由于只有一个驱动滚轮(roller  No.  4)的影响, β4  可以改变的,而其他的仍然是零,工件作出了协调的运动. 当β4的比例较小,va也小. 圆柱体轴向摩擦力,滚轮最大轴向摩擦力,汽缸产生弹性滑针对滚轮. 轴向运动之间各滚轮和工件协调弹性滑动. 因此,va是:

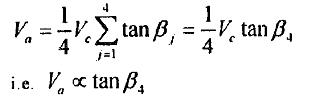
在理论曲线的斜率k'可以按下列公式计算:

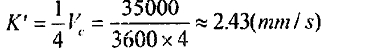
k=3.06mm/s的实验曲线. 因此,在考虑到各方面的实验,两个斜坡上可被认为是大致相等. 当β4  比较大, 滚轮与工件之间大于最大轴向摩擦力大于最大摩擦力, 工件产生摩擦滑动抵抗滚轮存在滑动摩擦力由于窜动的存在. va不再随着tanβ4  的增加而增加,而是逐渐减小

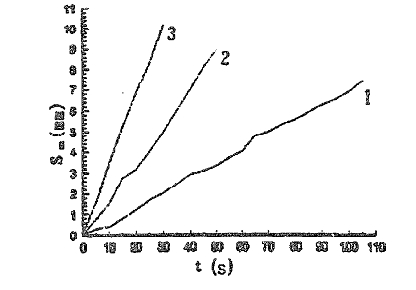
(2)以下三个实验,工件的不协调轴向窜动随之改变。由同一螺旋角度来衡量的一个主动滚轮及两个，三个主动滚轮 。三曲线之间的SA和V显示在 研究结果显示,在图7. 随着滚轮数量的增加,va逐渐增大.

Va 3 >  Va 2 > Va1

当驱动滚轮的数量变化时, 度气缸的非兼容轴运动将会有所改变. 随着同一螺旋角影响下滚轮数量的增加. 兼容的分量越来越大,但互不兼容的分量越来越小. 换句话说,工件的轴运动将转化为兼容的问题. 因此,va越大,轴向窜动越由β角所决定. 四辊有相同的螺旋角. va为:

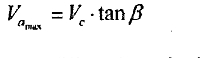
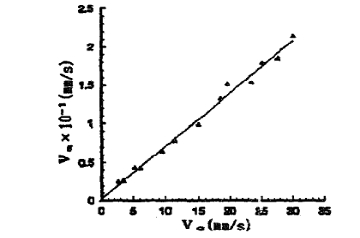
3.2.2 圆形速率的影响

螺旋角从平衡位置+2"对4号驱动滚轮的影响。, 工件将影响轴向窜动（例如图 8）所显示va-VC的曲线,后者表明va是与VC成正比的, 曲线的斜率大约是0.00708。因为β4=+2实在太小, 工件相对每一滚轮没有形成轴向窜动. 因此,相对与轴滚轮和工件之间的运动是完全协调的弹性滑动va为

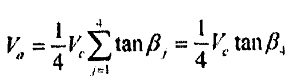
va正比于ve。理论曲线的斜率K*,可以按下列 方程K"=0.25tan4=0.25tan2'=0.00873wherek=0.00708mm/s. 因此,在考虑到各方的实验,协调的两个斜坡上可被认为是大致相等.

4结论

1. 因为制造及装配的偏差. 工件的中心线与滚轮轴线不平行. i. E。他们没有在同一平面,在他们之间 有一种螺旋角β. 存在β是发生轴向窜动的主要原因. 重力的影响,工件的轴线方向,也是轴向窜动的一个原因.

2. 单个滚轮和工件的相对轴向窜动包括弹性滑动与摩擦滑动,当轴向摩擦滑动没有出现在工件和单滚之间, 工件和滚轮的轴向窜动被他们的弹性滑动完全抵消, 存在关系：

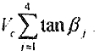
3轴向窜动可以分为完全的和不完全的,有很大的窜动力在的轴承之上, 虽然不完全的窜动还没有被定义，当存在不完全的窜动时，将造成滚轮和工件之间的磨损. 轴向窜动常被定义在一个特定的滚轮架上而言的。它的窜动速度的大小和方向是固有的.

4合理调整轴运动,使不兼容的分量尽可能小和 兼容分量尽可能大从而减小轴向窜动.

5随着滚轮数量的增加相同β角下的轴向窜动将增大,但不兼容的部分减少. 随着兼容部分的增加工件的轴向窜动速度将增加当轴向滑动摩擦发生在滚轮和工件之间时. 轴向窜动将被弹性摩擦和滑动摩擦所协调，但Vc并不与βj成正比 。关系如下

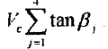
参考资料：

(1) Z Wang. 焊接机械设备教材，甘肃兰州工业大学， 张培源(1992)pp85-98

(2)武汉材料技术研究所，南京化工研究所,与华南工学院，水泥生产机械设备,      建筑工业出版社，中国北京,(1981)pp,184-187

(3) J . Halling(ed.)， 麦克米伦出版社,(1975)pp. 174-200