摘  要

计算机图像生成系统常常以一个平面多边形网格来描绘曲面，如此当被着色之后可还原一个平滑的曲面外观。冯氏着色是一种众所周知用于生成逼真的着色效果的算法但它并未在实时系统中使用，由于其求值每个像素需要三次加法，一次除法，一次平方根缘故。我们描述了一个新的构想用于冯氏着色，这将减少每个像素的计算量至只有二次加法用于简单的朗伯反射和五次加法和一个存储器参量用于冯氏完全反射模型.我们也会展示如何继承我们的方法去计算镜面反光使用从场景中视点的有限的距离而不是通常假设的无限视点距离。这个方法可以在硬件中实现用于实时应用程序或者在软件中来加速图像生成这可用于几乎任一个系统。

关键词：着色，快速，冯氏

引言

绝大多数计算机图像生成（CIG）系统以一个平面多边形网格描绘曲面因为多边形可以被快速转换和渲染当使用众所周知的算法的时候。尽管多边形表现的是图像生成方法的假象但通常这对于观察者来说是不感兴趣的,（见 图示1）,这些系统通过变化多边形面的亮度变化试图还原表面的平滑外观.这种着色操作的效率对于CIG系统的性能是取决定性作用的，因为它必须在每张图像上处理一百万或更多的像素.尽管用于多边形的真实着色的那些算法是众所周知的，实时CIG系统并未使用这些算法由于它们需要在每个像素上执行的大量运算。这篇文章描述了一个新的冯氏着色公式相对于前一个公式来说可以大幅度减少运算量. 同时这个新的公式是很好地被实现于用专用的硬件来实时显示,它同样也合适用软件实现用于各种各样的显示系统.读者如果不熟悉表面表现或着色可参考标准的图形文本了解更多的信息，[Newman and Sproull ,1979;Foley and Van Dam,1983].

背景

为了简单起见,假设着色的输入由三角形,屏幕上的坐标,法线向量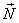组成，以及由每个原曲面上顶点指定的.这个公式可被扩展用于4边或更多边的多边形.

着色算法必须决定一个三角形中每个点的亮度从表面的法线向量和一个到光源的向量,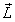.光源被假设为在无穷远处因此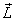独立于那个光照耀的点.我们将以漫反射开始,

，

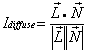稍候将展示如何扩展这个结果来包含冯氏高亮模型和一个已扩展的高亮模型。

高洛德着色：最常用的用于实时系统中的着色方法高洛德着色[高洛德,1971]，通过每个顶点间的线性插值来计算每个点的亮度.这个方法在实时系统中非常受欢迎因为它生成可接受质量的图像只要每个像素一次加法即可，但这个着色有几个令人不安的特性，（1）在确定的，可见的角度下移动物体将趋向于“水平飞行”.（2）表面表现为阴暗的白垩的,（3）图像表现出显著地马赫波段,夸张了不连续顶点间的亮度跨度.图示2是高洛德着色过的国际象棋棋子.

冯氏着色：冯氏着色，[冯氏,1973]，消除“水平飞行”和无光面并且减少马赫波段，但是并没有，据我所知,被用于任一个实时系统是由于大量的计算是必须的究其缘由为其常用的公式.冯氏方法决定每个点的亮度通过使用了一个近似于表面的法线，这个法线是从真正的在顶点中定义的表面法线之间通过线性插值而得到的.

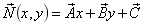
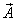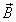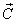,,被选择插值横贯多边形的法线,插值用于连续的x，y值和照度模型求值需要每像素七次加法,六次乘法,一次除法和一次平方根计算.但它并未实现,据我所知.图示3是一个冯氏着色的国际象棋棋子.Tom Duff 已经展示,在[Duff，1979]，冯氏着色可被实现的更有效率通过组合插值和反射方程.

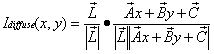
上面方程可以被重写为

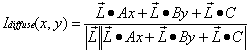
执行点乘运算和扩展向量的数学运算变为如下所示

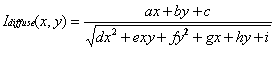
和

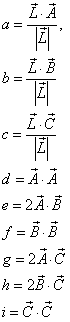
使用于先前的不同，这个格式可以求值通过三次加法，一次除法一次平方根每个像素.这是一个实质的节约上面的冯氏公式但是除法和平方根还是代价太高了对于实时下使用.

一个新方法

为了显示目的我们不需要求值反射方程；一个好的近似方程将足够胜任.近似方程引入的误差是不关紧要的因为冯氏法线插值和反射方程已经是近似的.一次泰勒级数广泛用于近似函数,比如正弦和对数操作，用多项式。较少的使用，二次

用于近似反射方程。

泰勒级数用于两个变量的函数是：

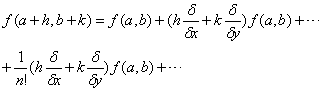
移动三角形从而使（0,0）位于其中心，展开项使用二阶泰勒级数得到

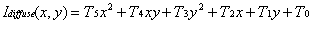
和

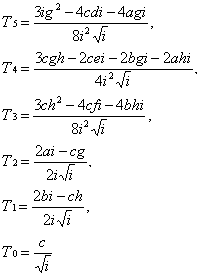
使用这个展开过的公式和与前一个公式的差异，亮度的求值可以只要每像素二次加法.

这个方法可以被扩展来处理冯氏镜面反射模型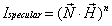，,通过泰勒级数来求值点乘和查询表来计算幂乘.（一个1K 字节的表允许幂乘到20次以不到百分之一的误差同时一个8K字节的表可幂乘到164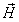）.是一个向量朝着最大高光值的方向，此方向介于光源方向,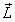和眼睛的方向,.

.

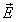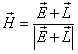眼睛，类似光源，被假设处于无穷远处.冯氏反射方程 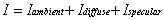.现在可以求值只要每像素五次加法和一次内存操作（环境反射成分可以卷进漫反射的级数之中而镜面反射级数可以测量以允许幂乘表的直接访问）.它应该可更简单如果配置硬件来做这些操作，那每个像素可在100纳秒内处理完成.

在我们的新方法中额外的计算必须用于计算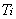，而它的补偿是大量减少多边形每像素的计算量.

这个估计是基于以下假设:(a)算法被实现于连续处理器的常规设计之中,

(b)现代硬件，时间用于浮点加法，乘法以及内存引用是相差不大的(c)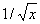的运算量需要大约10次操作(d)通用的子表达式已从公式中移除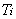.此方法的时间和分析实现于光栅试验台下[Whitted and Weimer，1982]也支持一个10像素保本的点.这保本点可以更小在我们的方法中如果有简易的硬件被加入来做这些加法和表查询相对比的话.当然,专用硬件可以设计用于其他方法但是它会更加复杂且可能不会这么快速.图像我们生成的使用这种近似方法是不易察觉的从那些使用冯氏方法生成的.对于那些大于60度以上的曲率多边形,这个新的扩展公式生成着色将会显著不同于冯氏着色但是如此大的曲率应该从不通过单一的多边形来展示.

走的更远

尽管多项式的形式我们必须用于每个像素上求值的是不依赖于源反射方程.

我们可以使用更详尽的模型.一个有用的扩展是提供一个有限距离的视点，这需要到视点的向量,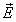，多次变化的穿过场景。如此变化的结果在镜面反射部分会产生更自然的照明效果在通过投影渲染的场景之中.同时将会更明显当在场景内有平坦的表面时因为用无穷远视点的冯氏着色就好像平坦着色一般，使用同一种亮度来渲染所有类似的表面.图示4是用无穷远视点的冯氏着色和真实投影距离的冯氏着色的比较图.视点在有限距离的镜面部分的反射方程现在变为这样

.

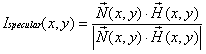其中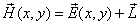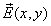，插值穿过三角形的视点向量.这个可以像先前一样被展开.

.

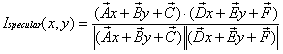在执行点乘运算和扩展向量的数学运算之后像先前一样，如下所示:

.

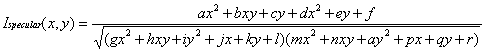和

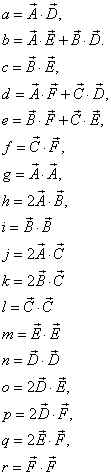
以及相对于位置（0,0）的泰勒级数展开项，如下所示：

.

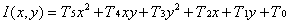和

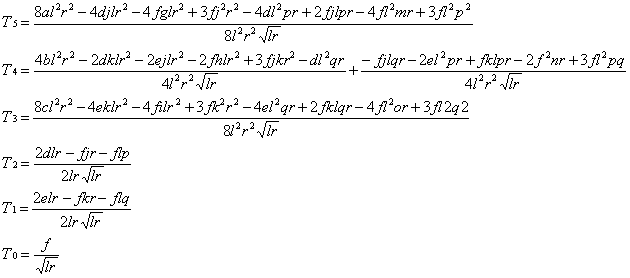
总结

我们已经展示了计算机图像生成系统可以使用冯氏着色的同时每个像素只比高洛德着色多一点的计算量.这个结果应该允许实时系统生成更逼真的场景和在传统的系统中更快速地生成图像.

为了测试这个方法,我们已经实现它用作一个光栅测试床的子路由着色器,渲染图示4有着14620个多边形在2048x2048分辨率下在一个DEC微型VAX-II下运行所用的CPU时间是

渲染方法        CPU时间      注解