摘要

宽度优先搜索(BFS)算法是许多图形处理应用程序和分析工作负载的基础。虽然图形处理单元(GPU)提供了大量的并行性，但是在GPU上实现高性能的BFS算法还是需要高效调度大量GPU      线程和有效利用GPU内存层次结构。在本文中，我们提出了一种基于GPU的BFS算法——Enterprise，它结合了三种技术来消除潜在的性能瓶颈:(1)通过构造一个没有并发线程争用的边界队列来简化GPU线程调度，同时不包含重复的边界，并且对自顶向下和自底向上的BFS都进行了优化。(2) GPU工作负载均衡，根据不同的出度数对边界点进行分类，从而利用GPU的所有大小的并行粒度，这大大提高了线程级的并行性;(3)基于GPU的BFS方向优化量化了关键顶点对方向切换的影响，从而在有限的GPU共享内存中有选择地缓存少量关键顶点，这减少了昂贵的随机数据访问。我们已经用不同的GPU设备用各种图的数据对Enterprise进行了评估。2014年11月，Enterprise在NVIDIA Kepler K40上实现了760亿条每秒的穿越边(TEPS)，在图500中排名第45位的两个GPU上实现了1220亿条每秒穿越边。在GreenGraph 500(小型数据类别)中，Enterprise以4.46亿条穿越边（TEPS）/瓦的成绩成为了能源效率最高的算法。

1. 介绍

宽度优先搜索(BFS)算法是许多分析工作负载的构建块，如单源最短路径、中介中心性[16,31,32,42]和亲密中心性[37,40]。值得注意的是，图500基准使用幂律图上的BFS来评估高性能的被设计用来运行数据密集型应用程序的硬件架构和软件系统 [1]。在这项工作中，我们特别感兴趣的是加速可以在生物医学细胞[26]、WWW[9,25]和社交网络[17,27]等广泛的应用中找到的在幂律图上的BFS遍历。

传统的(自顶向下)BFS算法从图形的根开始，并检查与之所有相邻(或相邻)顶点的状态。如果有任何未被遍历过的相邻点，算法会将其识别为一个边界点，并将其放入我们在本文中称为边界点队列的队列中，然后将其标记为已访问的。检查当前遍历层次的结果是，边界点队列由所有刚刚访问过的顶点组成，这些顶点将用于下一遍历级别的展开。由此，BFS迭代地选择边界点队列中的每个顶点，检查其相邻的顶点，并标记刚访问的这个顶点。展开和遍历的过程一层一层地重复，直到图中没有未访问的顶点。对于最近提出的自底向上BFS算法[10]，工作流类似于将不同的顶点标识为边界点。显然，边界点队列是BFS算法的核心——在每一层，BFS从前一层检查准备的边界点队列开始，以一个新的边界队列结束，该队列将用于下一层的扩展。

图形处理单元(GPU)不仅提供了大量的并行性(在100k线程中)，还提供了快速的I/O(具有100s GB/s的内存带宽)，这使得它成为运行BFS算法的优秀硬件平台。不幸的是，尽管最近的尝试[21,33,36,24]取得了显著的进展，但运用GPU的全部力量来实现高性能BFS仍然具有极大的挑战性。在本文中，我们主张高性能的BFS系统应该通过对大量GPU流处理器的高效管理和独特的内存层次结构来仔细匹配GPU的硬件特性。

本文提出了一种基于GPU的BFS系统Enterprise(企业号是1976年为美国宇航局建造的第一架航天飞机的名字。)，该系统充分利用了GPU的高线程数和大内存带宽优势，对BFS的执行流和数据访问模式进行了定制。Enterprise在单个NVIDIA Kepler K40上可实现760亿TEPS/秒，在两个GPU上可实现1220亿TEPS/秒和4.46亿TEPS /瓦特，在2014年11月，这个成绩在图500上排名45，在GreenGraph 500小数据类中排第1位。这是通过三种新技术的设计实现的:

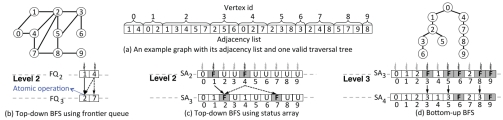
图1:(a)一个示例图及其邻接表和一个有效的BFS遍历树(可能存在多个有效的BFS树)。我们在整篇论文中都使用了这个例子。自顶向下BFS使用(b)中的边界点队列或(c)中的状态数组，而(d)则是自底向上BFS所用。状态数组中的数字表示访问顶点的层次。F和U的标签分别表示边界顶点和未访问顶点。在(c)和(d)中，分配给非边界顶点的灰色线程将空闲且不做任何工作。

首先，简化的GPU线程调度是通过两个不同步骤生成的边界点队列来实现的:先扫描当前级别的图的状态数组，然后根据前缀和生成边界点队列。在将边界点入队时，需要原子操作来确保队列中每个边界顶点的唯一性，然而，对于GPU来说，这种操作可能会导致大量GPU线程的开销。通过将队列生成分为两个步骤，Enterprise不仅可以通过并行地更新和访问状态数组来消除线程同步的需要，还可以从队列中删除重复的边界，从而避免将来可能无用的工作。这进一步结合内存优化来加速自顶向下和自底向上的BFS。评估表明,尽管它可能需要花费少量的时间生成队列，但我们的GPU线程调度可以将整个BFS运行时间加快37.5倍。

其次，通过将边界点分类来平衡GPU的工作负载。为了减轻线程间工作负载的不平衡，Enterprise根据外部性(到相邻顶点的边的数量)将边界点分类放到多个队列中，并为每个队列分配不同数量的线程。具体来说，Enterprise创建了四个不同的边界点队列，分别对应于Thread、Warp、Cooperative Thread Array (CTA)和Grid[4]。例如，企业可以为输出度小于32的边界分配一个Thread，为输出度小于256的边界分配一个Warp。企业甚至可以将一个block上的所有线程分配给一个边界点，以处理极端高的出度数(例如10^6)。以前的工作使用固定数量的线程(通常为32或256)，其中静态分配常常导致线程之间的工作负载倾斜[21,33,23,29]。边界点分类大大缓解了这一不平衡,可以为上面提出的GPU线程调度技术提供1.6-4.1倍的加速。

第三，在Enterprise中开发出了GPU感知的方向优化，以此在GPU上高效运行自底向上的BFS。具体地说，我们提出了一个使用边界点队列中关键节点的比率定义的新参数，通过这个参数来确定在GPU上由上而下到由下到上的一次性切换的开销。这个参数在不同的图中是稳定的，不需要像前面的[10]方法那样进行参数调整。更重要的是，Enterprise有选择地缓存GPU共享内存中的关键顶点，以减少昂贵的随机全局内存访问。有趣的是，这种基于共享内存的缓存的大小很小，只有48kb，当缓存几千个关键顶点时，可以帮助自底向上BFS减少高达95%的全局内存事务。

我们所知,Enterprise是第一个不仅利用各种各样的GPU线程组来平衡不规则的工作负载，同时使用不同的GPU缓存来减轻随机访问的基于GPU的BFS系统, ,这两点都是幂律图在进行遍历时所固有的特性，所以在现代GPU上对其的优化十分具有挑战性。Enterprise可用于支持多种图形算法，如单源最短路径、直径检测、强连通分量、中介中心性等。

本文的其余部分组织如下:第2节介绍了本文中使用的GPU、BFS和图的背景。第3节介绍了在GPU上运行BFS算法的挑战。第4节描述了三种技术及其优点。我们在第5节中展示了Enterprise的整体绩效和能源效率。第6节讨论了相关工作，第7节总结。

2. 背景

2.1广度优先搜索

传统的(自顶向下)BFS算法在每个层次上进行扩展和检查，即从每个边界(最近访问的)顶点v开始，检查相邻的顶点w是否首次访问。如果是，则v成为父结点，w也被加入到边界点队列中。

边界点可以通过两种方式生成。在图1(b)的第一种方法中，称为基于边界点生成[30]的原子操作，在第2级分配两个线程来检查FQ2队列中顶点1和4的邻接表，两个线程都想把顶点2加入FQ3。在这种情况下，使用原子操作(例如，CUDA[4]中的atomicCAS)来确保FQ3没有重复的边界，其中最先结束的线程将成为顶点2的父线程。如果没有原子操作，顶点2将被入队两次，导致第3级的工作冗余。

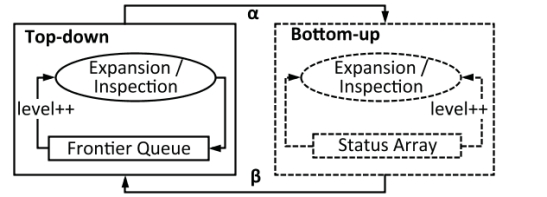
图2:混合(方向优化)BFS。

由于线程间同步在GPU上代价高昂，第二种方法[24,36]使用名为状态数组(SA)的数据结构来跟踪图中每个顶点的状态。状态数组基本上是由顶点ID索引的字节数组。顶点的状态可以是未访问的、边界的或已访问的(由其BFS级别表示)。在每一层，每个顶点被分配一个线程，而只有那些在边界点上工作的线程才会执行扩展和检查。因此，如图1(c)所示，虽然第2级将使用10个线程，但只有在顶点1和4上的2个线程会工作。这种方法的优点是不再需要原子操作——顶点1和4都可以是顶点2的父节点，并且可以按顺序执行顶点2状态的更新。在这里，与第一种方法不同的是进程最后结束的那个点会成为顶点2的父结点。

使用自顶向下方法初始化混合BFS，并在切换参数达到预定义阈值时在自顶向下和自底向上之间切换方向。图2展示了混合(方向优化)BFS的工作流程。自顶向下的BFS旨在识别将边界点和未访问的顶点连接起来的边，而自底向上的目的是识别边界点及其连接的已访问的顶点。本文正式将边界点定义为:

定义(边界点)令v为图g的顶点。在第i层，v为边界，如果：

•自上而下BFS:v在i-1层被访问;

•自下而上BFS: v在0 – i-1层中未被访问过。

使用图1中的相同示例，在第2级，自顶向下算法选择顶点{1,4}作为边界。相对的，自底向上算法使用未访问的顶点{3、5、6、8、9}作为级别3的边界。当自底向上发现顶点{3,5}连接到访问过的顶点2时，它们被遍历标记为以2作为父节点的顶点。类似地，顶点8被遍历标记为以7作为父节点。

方向切换的目标是减少潜在的大量不必要的边缘检查。混合BFS在此过程中可能会两次切换方向，即，从自上而下到自底向上和自底向上到自顶向下，每一个切换都与一个参数相关联。在图2中,α是通过mu和mf的比率计算出的,其中mu表示未访问的边数,mf表示将被自顶向下算法访问的边;β是通过n和nf的比例计算出的,其中n表示图的顶点数和nf表示边界队列中的顶点的数量。目前阈值是启发式（探索式）确定的。

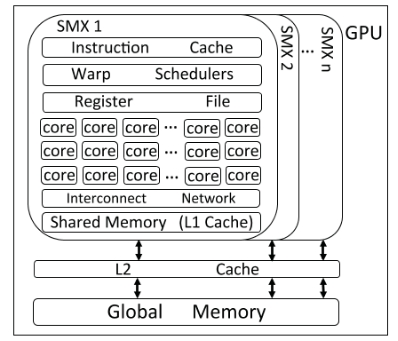
图3:GPU架构的简化视图。

在BFS的最后阶段，为了避免图中的对Enterprise来说既没有必要也没有好处的长尾现象，我们从自底向上到自顶向下进行了切换，。在本文中，我们将展示构建一个高效的混合BFS系统需要大量的GPU感知优化，包括稳定的方向切换参数、关键顶点缓存、流线型GPU线程调度和工作负载平衡。

2.2通用的GPU

在本节中，我们将主要介绍GPU硬件，以NVIDIA Kepler K40为例[8]。K40由15个流媒体处理器(SMX)组成，每个处理器有192个单精度CUDA核和64个双精度单元。每个GPU线程运行在一个CUDA内核上，SMX将32个线程安排在一组中(称为Warp)。图3展示了GPU架构的概述。

一个SMX最多可以支持64个warps。一个warp中的所有线程都以单指令、多线程方式执行。但是，如果一个warp中的线程有不同的控制路径，那么warp会依次执行所有的分支，并禁用不在该路径上的所有线程。这被称为分支发散问题，如果存在的话，可以大大降低SMX的利用率。

每个SMX都有4个warp调度程序，它们轮流选择4个warp，并从已准备好执行的warp调度程序中发出指令。跳过由于长延迟的数据访问而没有准备好的warp。通过在每个SMX中的超额线程，数据访问可以与调用重叠。

协作线程数组(CTA)，线程块，由多个warps组成，通常是1到64个，它可以用来运行大量的线程。GPU上所有CTA的集合称为一个Grid。CTA的数量及每个CTA中的线程数是可配置的。CTA中的每个线程都有一个唯一的线程ID，每个CTA都有自己的CTA ID。有了这些内置变量，就可以识别grid中的每个线程，并调度不同的线程处理不同的数据。

表1:图的说明

Kernel定义为运行在GPU上的任何函数。通常，一个内核可以使用相对确定数量线程的不同的并行粒度。(线程、warp、CTA或grid)。Kepler引入Hyper-Q来支持并发内核执行，换句话说，当几个内核在同一个GPU上执行时，Hyper-Q能够将它们安排在不同的SMX上并行运行，从而充分利用所有GPU资源。

GPU内存层次结构。每个SMX都有大量寄存器，例如，每个K40 SMX有65,536个寄存器。每个线程最多可以使用255个寄存器，并为每个时钟周期执行4个寄存器访问。此外，每个SMX提供软件可配置的共享内存(L1缓存)，用于内部传输和CTA内部数据通信。每个K40 SMX有64 KB的共享内存。与CPU上的L1缓存不同，可以在程序运行时分配16、32或48 KB的共享内存。一旦加载，共享内存中的数据对一个CTA中的所有线程都是可读和可写的。

GPU还具有所有SMX共享的L2缓存和全局内存。K40有1.5 MB L2和12GB的全局内存。每次全局内存访问都返回一个数据块，该数据块根据类型包含32、64或128个字节。如果一组线程恰好访问同一块中的数据，则只执行一个硬件访问事务。通过这种方式，将全局内存访问合并为更少的传输次数，K40能够实现接近300GB/s的DRAM带宽。

表2:CPU (Xeon E7-4860) vs. GPU (K40)内存:大小和访问延迟(CPU和GPU周期)[28,4]

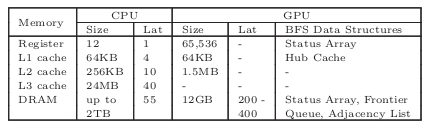
表2总结了CPU和GPU内存层次结构。注意，K40没有L3缓存。我们无法为寄存器和共享内存找到正式的延迟数，但是我们的测试表明，它们至少比全局内存快一个数量级。在这项工作中，我们利用了GPU支持的并发内核和不同并行粒度来动态匹配BFS工作负载，并对各种BFS数据结构使用了不同的GPU内存，例如对关键顶点使用共享内存。

GPU硬件性能计数器。今天的GPU可以支持100多个硬件指标[5]。在这项工作中,我们的目标是理解内核性能,GPU I / O吞吐量和我们系统的能源效率,包括不同内核的时间表,利用内存加载/存储功能单元(ldst_fu_utilization),由数据请求引起的停机的百分比(stall_data_request),全局内存负载事务(gld_transactions),IPC和性能。我们使用两个NVIDIA工具，即nvprof和nvvp。

2.3图形测试基准

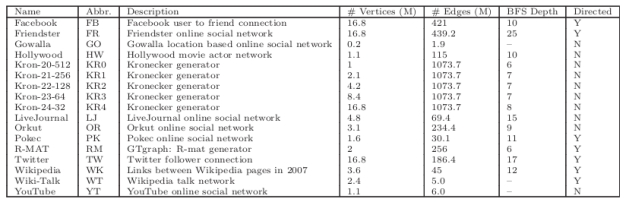
本文一共使用了17张图，如表1所示，顶点数为100万 - 1700万，边数为3千万- 10亿。对于无向图，我们将每条边算作两条有向边。包括Facebook[19]、Twitter[27]、Wikipedia[7]等11个真实世界的图，以及斯坦福大学大型网络数据集[6]中的LiveJournal、Orkut、Friendster、Pokec、YouTube、Wiki-Talk和Gowalla社交网络图。此外，我们使用了两种广泛使用的图生成器，Kronecker[1]和递归矩阵(R-MAT)算法[13][3]。两种生成器都带四种可能性A,B,C和D  = 1.0−A−B−C，Kronecker生成器产生的Kron-Scale-EdgeFactor图，其中有2^scale个顶点，每个顶点拥有EdgeFactor的平均数的出度。在这项工作中，我们对Kronecker使用(0.57,0.19,0.19)的(A, B, C)，对R-MAT图使用(0.45,0.15,0.15)。值得指出的是，真实图和合成图都具有微型世界特征——由于大多数顶点的出度数较小，占总边数的百分比较小，因此存在大量的有较多出度的顶点。

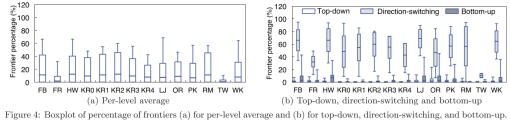
图4.边界点所占百分比的盒图

3.设计的挑战

挑战1:好好利用GPU线程

消除GPU生成边界队列需要的原子操作是之前的重点工作(24,33,29,36,35,30]，它只解决了一半的问题——队列应该仅由边界点（需要探索的下一层的顶点）构成。使用状态数组进行下一层遍历，尽管避免了原子操作，但是会为每个顶点分配一个GPU线程，而不管这个点是否是边界点[36,24]。这种低效的方法会过度申请GPU线程，因为在大多数遍历层次上，大多数顶点都不是边界点。或者，另一个工作[33]通过warp和历史剔除生成边界队列，但是同样，这种方法不能完全避免跨扭曲的重复顶点被加入队列。图4(a)显示了不同图中每一层边界点百分比的箱线图，其中显示了平均值和最大值百分比以及标准差。请注意，这里的数字包括自顶向下和自底向上方向的边界点。结果显示，图中每层平均有9%的边界点，标准差为15%。其中R-MAT图的平均比例最大，为11%，最大值为57%，而Twitter的平均比例最小，为1%，最大值为10.2%。如果在每一层为每个顶点分配一个线程，平均至少有31%的线程会空闲。因此，关键是有一个只包含边界点的队列，而不是将宝贵的GPU线程浪费在那些没有工作要执行的队列点上。

由于需要在自顶向下和自底向上之间切换方向，从而通过关注两组不同的顶点(自顶向下访问vs.自底向上访问)来生成边界，这进一步加剧了这一挑战。为了说明这个问题，我们在图4(b)中用BFS遍历方向表示边界的百分比。一般来说，自底向上的级别比自顶向下的级别具有更多的边界点，即1.5%对0.4%。特别是，从自顶向下切换到自底向上时，同一级别队列的边界点平均最多为52%。在这个级别上单独使用状态数组仍然是低效的。通过以上观察，Enterorise开发了新的GPU线程调度，其目标是准备一个根据GPU内存层次结构做方向优化的边界点队列。

挑战2:在GPU线程之间平衡工作负载

这一挑战源于边界点的出度数存在着巨大的差异事实。如果一个边界点有更多的边，分配给它的GPU线程自然需要进行更多的扩展和检查。为了说明这种不平衡，我们在图5中绘制了两个社交网络的边数的CDF，其中Gowalla和Orkut的平均出度分别为19和72。在Gowalla中，86.7%和99.5%的顶点有小于32和256条边。相比之下，Orkut中国，有32条边以下的顶点所占的比例较小(37.5%)，而有32到256之间的顶点所占比例较大(58.2%)。此外，在Gowalla和Orkut中，有一小部分(0.5%和4.2%)顶点的边超过256条，且尾部较长，有约为30K边。

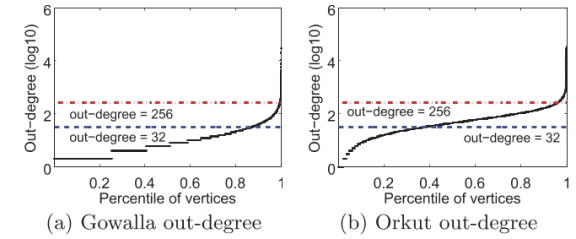
图5:顶点按出度排序的出度累积分布函数(CDF): (a) Gowalla (b) Orkut。

静态地分配固定数量的线程(例如，一个warp或CTA)是低效的，因为每个层次的运行时间将由工作量巨大的线程控制。另一个效率低下的原因可能是线程数和工作负载不匹配。例如，如果一个CTA被分配在有少于32个相邻顶点的边界点上工作，那么这个CTA中的200多个线程将没有工作要做。在另一个极端情况下，一些具有非常多出度的边界点将需要多个CTA，例如，我们检查的一些图的顶点最多有106条边。为了解决这一挑战，Enterprise引入了一种新的方法，根据出度数对边界点进行分类，并在运行时分配适当的GPU并行粒度。

挑战3:让自底向上的BFS适应GPU

在GPU上实现方向优化的BFS本身就是一个挑战。方向优化的BFS最初是在[10]中的多核CPU上提出并实现的，但是如果没有进一步的优化，就无法在可以运行数千个线程的GPU上高效地运行，而全局缓存的大小(例如12GB)和速度(例如200-400个周期)相对较小。

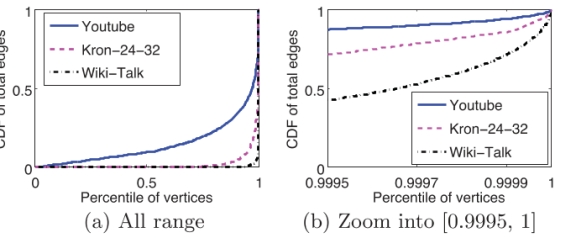
图6:Youtube、wikitalk和Kron-24-32图中所有边的CDF。顶点按出度排序:(a)为所有范围内的顶点(b)缩放范围[0.9995,1]。

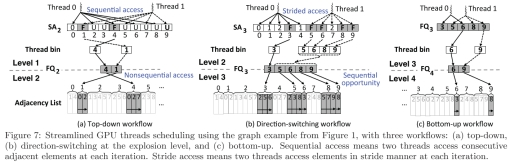
图7 使用图1中的示例来进行简化的GPU线程调度。（a）自上而下（b）爆炸层的方向转换（c）自下而上。顺序访问意味着两个线程在每次迭代中访问连续的相邻元素。跨步访问是指两个线程在每次迭代中以跨步方式访问元素。

与此相反，如表2所示，现代CPU有几十个拥有具有较大的L3缓存和较短的访问延迟的主存的内核和线程。幸运的是，大量的寄存器和可配置软件的共享内存(L1缓存)可以弥补GPU在全局内存上的不足，这可以用来加速像BFS这样的内存密集型算法。

基于CPU的自底向上BFS使用状态数组支持未访问的顶点的检查，自顶向下和自底向上之间的方向切换取决于未探索的边的数量。在Enterprise中，基于GPU的自底向上BFS利用一小组称为中心顶点的高度连接的顶点。形式上，我们定义一个中心顶点如下。

定义(中心顶点):若v是图G的一个顶点 .定义顶点v是一个中心，如果它的出度大于阈值τ。

τ是依图而变的,例如,在Twitte中，定为100 K s。幂律图中少数中心顶点与大量顶点相连接是很常见的。图6显示了所有边的CDF和顶点范围[99.95%，100%]的放大视图。对于YouTube图，可以看到330个hub顶点(即， 0.03%的顶点)拥有所有边的10%。类似地，Kron-24-32中的770个hub顶点(0.005%)拥有所有边的10%，Wiki-Talk中的96个hub顶点(0.004%)拥有所有边的20%。

我们基于gpu的自底向上的BFS最独特的特性为:1)Enterprise在本文所说的爆炸级（这一层需要访问大量的中心点）进行方向切换。在这项工作中，我们发现边界点队列中中心顶点的数量可以作为更好的方向切换的指示器，者可以很容易地在GPU上实现。更重要的是，缓存中心顶点对自底向上的BFS非常有益。

4. Enterprise:基于GPU的BFS

4.1简化GPU线程调度

结合状态数组和边界点队列的强大功能，Enterprise可以通过扫描状态数组在每一层生成边界点队列，从而实现对GPU线程的流线型调度。在每个层次上，Enterprise都以类似于[36,24]的方式识别边界点并更新状态数组。完成此步骤后，Enterprise将分派GPU线程扫描状态数组中的顶点。当发现一个边界点时，该线程将把这个顶点存储在它自己的线程库中。所有线程库都存储在全局内存中。接下来，使用前缀和计算每个库在边界点队列中的偏移量[34,22]。最后，将每个库中的边界点并行复制到队列中。总之，避免线程同步(使用数组)和减少下一层的空闲线程(使用队列)的好处是显而易见的。然而，正如我们所展示的，BFS的方向会导致在每层上边界点数量的巨大差异。

为此，Enterprise计划使用三个GPU线程用于自顶向下、方向切换和自底向上的队列生成工作流，以优化所有情况下的内存访问。状态数组、前沿队列和邻接表驻留在GPU全局内存中，随机访问全局内存只能实现3%的连续读取带宽。为了最大化总体性能，优化BFS不同阶段的访问模式至关重要。

自上而下的工作流。在这个方向上，Enterprise使用GPU线程以交错的方式扫描状态数组。对于图7(a)中的示例，在第1级分派了两个线程:线程0检查5个顶点{0,2,4,6,8}的状态，而线程1检查其他的顶点{1,3,5,7,9}。这部分工作执行顺序访问内存中的状态数组。当前缀和完成时，线程0和1将并发地将它们自己的线程库复制到FQ2中。在这种情况下，FQ2将两个无序的边界存储为{4,1}，这将在第2级引入非顺序内存访问，即BFS在顶点1之前访问顶点4的邻接表。幸运的是，状态数组顺序访问的好处超过了邻接表随机访问的潜在缺点。对于自顶向下，状态数组中相邻的顶点不太可能成为同一级别的边界，因为只有少量(平均0.4%)的边界，如图4(b)所示。

图8:Facebook爆炸式发展前后的GPU线程调度和工作负载平衡的执行时间线。

方向切换 (explosion-level)工作流。这种情况不同。在这里，GPU线程被分配到状态数组的特定部分进行扫描。使用相同的示例，在第2级，将再次使用两个线程:这次线程0检查5个顶点{0,1,2,3,4}的状态，而线程1检查5个顶点{5,6,7,8,9}的状态。与自顶向下的工作流不同，这种方法在扫描期间会导致跨区内存访问。接下来，在线程库中执行前缀和，在本例中，FQ3由{3,5,6,8,9}组成。性能优势来自于(自底向上)边界可能按顺序出现在队列中，从而导致下一层的顺序内存访问。在爆炸级别，相邻的顶点很可能都是未访问的，因为大多数顶点如图4(b)所示。这个工作流利用这个事实来加速下一层的遍历，例如，在第4层，加载顶点5和6的邻接列表是顺序的邻接内存访问，顶点8和9也是如此。

在爆炸的层面上, 相较于自上而下的工作流，这种方法将花费平均2.4×的时间扫描状态数组。例如，在好莱坞，使用自顶向下工作流的爆炸级别需要0.57 ms。相比之下，使用方向转换工作流将花费更长的时间0.86 ms。但这种方法将使下一层遍历的性能平均提高37.6%，例如，在爆炸级后的级别上的Hollywood 运行时间将从2.7 ms减少到2 ms。由于后一个步骤需要更长的wall clock时间，因此在所有图中，整体性能平均提高了16%以上，其中Facebook的改进幅度最大，达到33%。

自底向上的工作流。关键的见解是，对于自底向上，当前层的队列始终是前一个队列的子集，因为边界始终是未访问的顶点。我们没有继续使用状态数组，而是直接使用前一层的边界点队列来生成当前层的队列，如图7(c)所示。这是通过删除属于当前级别的顶点来完成的。这种方法消除了扫描整个状态数组的需要。在每层上只检查一个小的(快速收缩的)子集。例如，在第3级，FQ4是通过从FQ3中删除顶点{3,5,8}来创建的。我们的测试表明，这种方法在不同的图表中提供了3%的改进。

总而言之，这种技术增加了活跃在边界上并发出内存加载/存储请求的GPU线程的数量，我们将在实验中看到内存加载/存储函数单元的利用率显著提高。使用这个设计,队列在不同的图中仍然生成的很快，用时2.2ms到53.7ms,约占整体的BFS遍历用时的11%,提供了2×到37.5×的加速。图8显示了Facebook爆炸式增长时BFS的执行轨迹。显然，尽管生成前沿队列需要23.6 ms，但由于准备了一个良好的工作队列，新线程调度将扩展和检查的运行时间从490 ms减少到419 ms，净节省46 ms。

4.2 GPU工作负载均衡

现在，Enterprise可以快速生成良好的前沿队列，但是如果队列会导致工作负载不平衡，那么收益将是最小的。在这项工作中，我们认为在从前沿队列调度工作时，应该利用GPU的并行粒度，以确保较高的线程级并行性。理想情况下，每个线程，无论是否独立，在warp或CTA中，在每一层都应该有等量的工作(展开和检查)。为了实现这一目标，Enterprise根据边界点的出度(潜在的工作负载)对边界点进行分类，并分配匹配的并行粒度。与以前的工作不同，Enterprise侧重于在warp或CTA上使用线程[23,33]。这是由图中的大多数顶点都仅有小的出度这一事实所造成的。对于研究的图来说，小于32条边的顶点的平均百分比是68%，在Twitter上可能高达96%。

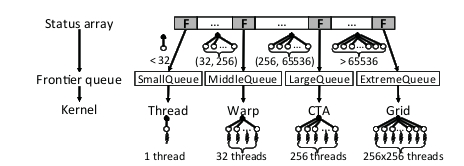
图9:GPU工作负载平衡。

Enterprise根据每个边界的出度，将前面技术生成的边界划分为四个队列:SmallQueue、middle queue、LargeQueue和ExtremeQueue。具体来说，小队列中的边界点小于32条边，MiddleQueue在32到256条边之间，LargeQueue在256到65,536边之间，Extreme-Queue在65,536边以上。在边界队列生成期间，每个线程根据它们的出度将发现的边界点放入四个线程库中的一个。在下一层中，将分配4个线程数量不同的内核(线程、warp、CTA和grid)在不同的前沿队列上工作，以平衡线程之间的工作负载，如图9所示。所有内核都是使用Hyper-Q支持并发执行的。

我们维护一个极值队列来处理具有高出度的顶点。例如，KR2中的一个顶点有超过250万条边。如果指定一个CTA来检查这个顶点，它将需要10,000次以上的迭代。正如我们在图5和图6中看到的长尾一样，这种类型的顶点存在于许多图中。随后，从这些顶点展开将需要相当长的运行时间，如果不进行特殊处理，可能会大大延长整层的遍历时间。使用整个grid可以大大加快执行,例如,在KR0实现了1.6x加速。

在图8(b)和(c)中，可以看到工作负载平衡前后运行时的变化。同样，尽管这种优化又增加了5 ms的开销来对边界进行分类，但是我们能够大幅缩短整个运行时间，从419 ms缩短到76.5 ms。特别是线程内核需要63.5 ms、Warp 需要17.8 ms和CTA内核需要10.5 ms，这三个内核之间存在明显的重叠。简而言之，与以前的方法相比，这种技术进一步消除了每个CTA和warp中的空闲线程，与第一种技术类似，这将导致GPU内存单元的更高利用率。

4.3基于Hub顶点的优化

方向切换参数。在这项工作中,我们发现调优参数α来决定何时从自上而下切换到自下而上是繁琐的。相反，由于中心顶点在爆炸级别上占很大比例，我们建议使用边界队列中中心顶点的比例作为方向切换的指示器。我们定义参数γ的正式名称为:

γ= Fh/Th×100%       (1)

其中Fh是边界队列中hub顶点的数量(每层收集)，Th表示hub顶点的总数量，可以在第一层非常快速地计算。我们的实验表明,γ是稳定而不需要手动调整。图10显示了所有图在γ∈(30，40)%时应切换方向,相较于α在2和200之间波动，是一个非常小的范围。在这项工作中,我们设置方向切换的条件为γ大于30。

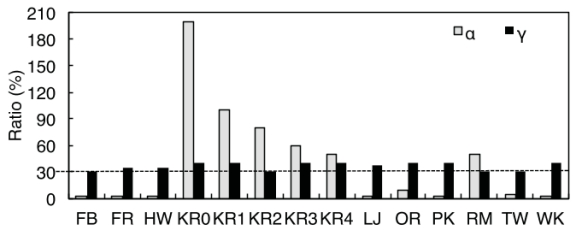
图10:方向切换参数的比较。

Enterprise平均在不同的图上自顶向下遍历4层，自底向上遍历8层，比之前的方法[10]快了大约1层。在Kronecker图中,使用α会检查分别在自顶向下和自底向上的4%和17%的边,避免了访问其余79%的边缘。使用基于我们中心顶点参数γ将检查自顶向下和自底向上的1%和36%的边。乍一看，Enterprise会检查更多的边缘，从而损害效率。幸运的是，正如我们所展示的，方向切换发生在由中心顶点控制的爆炸层，而自底向上遍历的重点是识别连接边界到最近访问的中心顶点的边。因此，中心顶点的良好缓存非常适合这两种场景。

中心顶点缓存。在这项工作中，我们建议在方向切换和自底向上时，将hub顶点缓存到GPU共享内存中，这可以大大降低随机全局内存访问的开销。这种好处是可实现的，因为自底向上的大量边界很可能连接到中心顶点。然而,因为GPU共享内存很小(64 KB),我们需要仔细平衡中心顶点缓存的数量和GPU的占有率（定义为运行在一个SMX上的活跃的warp与一个SMX理论上可以支持warp的最大数量(64个)的比例)。如果一个grid包含256×256个线程,K40意味着运行8个 CTA的会占用一整个流处理器,因此每个CTA只有6 KB共享内存来构造顶点缓存，可存约1000个中心。

Hub顶点缓存(HC)分两步实现。首先，在边界队列生成期间，Enterprise缓存上一层刚刚访问过的顶点的id，这些顶点id也具有较高的出度。我们使用一个哈希函数来计算存储每个顶点ID的索引，即HC[hash(ID)] = ID。其次，在边界识别过程中，Enterprise会加载边界点的邻接点，并检查是否缓存了任何邻接点的顶点ID。如果是这样，检查将提前终止，缓存的邻接点将被标识为该边界的父节点。在这种情况下，缓存将避免访问该邻接点在全局内存中的状态。

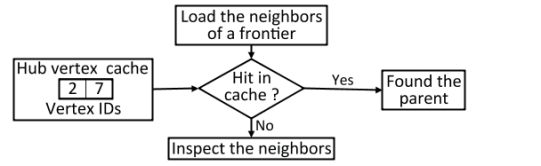
图11:Hub顶点缓存设计，使用图1示例图中的第4级遍历。

图11展示了hub顶点缓存的工作流。在本例中，Enterprise将顶点id{2,7}放在hub顶点缓存中，因为这两个顶点是在前一层访问的，并且具有较高的出度。在当前级别，Enterprise加载顶点3的邻接点{2,5,6}进行检查。当顶点2被缓存时，Enterprise将把顶点2标记为顶点3的父节点，并终止检查。另一方面，如果像顶点6这样的边界点没有缓存的邻接点，Enterprise将继续检查驻留在全局内存中的邻接点的状态。如图12所示，hub顶点缓存在各种图上非常有效，节省了10%到95%的全局内存访问。值得指出的是，缓存中心顶点对于自顶向下BFS的好处有限，因为它可能遇到的中心顶点很少。

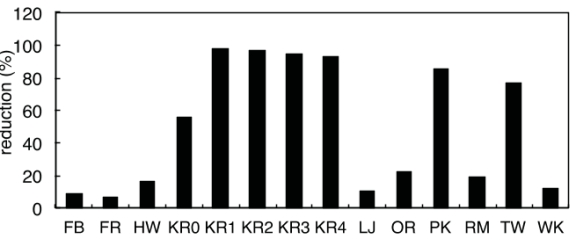
图12:中心点缓存缓存减少了全局内存访问。

4.4 多GPU的Enterprise

Enterprise利用一维矩阵划分方法[11]将图分布在多个GPU上。具体地说，每个GPU负责图中相同数量的顶点，因此也负责类似数量的边。我们把二维划分的研究留到以后再做。在遍历过程中，Enterprise分为三个步骤:(1)每个GPU通过从私有的边界点队列展开来标识私有状态数组中的当前级别顶点。(2)所有的GPU通信它们的私有状态数组，以获得最近访问顶点的全局视图。在这一步中，每个GPU使用一个CUDA指令__ballot()将私有状态数组压缩为一个位数组，其中一个位用于指示一个顶点是否被访问了。这种压缩将通信数据的大小减少了90%。(3)每个GPU扫描更新后的私有状态数组，生成自己的私有前沿队列。

5. 实验

我们已经用C++和CUDA在3000行代码中实现了Enterprise。源代码使用NVIDIA nvcc 5.5和GCC 4.4.7编译，优化标志为O3。在这项工作中，我们使用三个GPU: NVIDIA Kepler K40, K20和Fermi C2070。我们对如表1所示的图进行了测试。所有的图都用压缩稀疏行(CSR)格式表示。提供边的元组的数据集转换为了CSR格式，保留边元组的序列。大多数的图表都是排序的，例如Twitter和Facebook。我们不执行如删除重复的边缘或自循环的预处理。所有数据都用uint64类型表示，并被加载到GPU的全局内存中。计时开始于搜索信号被赋给GPU内核时；当搜索完成并写入GPU内存时，计时结束。对于每个实验，我们在伪随机选择的顶点上运行BFS 64次，并计算其平均值。每秒遍历的边(TEPS)计算如下:设m为搜索遍历的有向边数，计算任意多条边和自循环，t为上述BFS搜索所花费的时间。然后，用m/t计算TEPS。

5.1Enterprise性能

由于基于原子操作的前沿队列会慢得多，因此我们使用状态数组方法作为基线(BL)实现了方向优化BFS。在这里，我们使用CTA处理状态数组中的每个顶点，这比分配线程或warp要快得多。图13描绘了每次优化带来的性能改进，包括流线型GPU线程调度(TS)、GPU工作负载平衡(WB)、中心顶点缓存(HC)。

在所有的图上，流线型的 GPU线程调度是基线速度的2x到37.5×。特别是，Twitter (TW)获得了最大的加速，从0.4亿TEPS增加到15亿TEPS。原因是Twitter的最大边界点比例只有10.2%，平均每个级别只有1%的边界点。Kron- 20 - 512 (KR0)收益2×加速,达到340亿TEPS。一般来说，生成边界点队列平均消耗BFS运行时的11%。

GPU的工作负载平衡技术加快了所有图的遍历速度2倍以上,在第一个技术上平均2.8×。例如,LiveJournal (LJ)达到4.1×最大的改进,从9亿TEPS到37亿TEPS。在这个图中，总工作负载是均匀分布的，因此SmallQueue包含78%的边界点(或22%的工作负载)，MiddleQueue包含21%的边界(或58%的工作负载)，LargeQueue包含1%的边界(20%的工作负载)。

中心顶点缓存技术可帮助将性能提高55%。Facebook (FB)和Friendster (FR)都有一个小的收获，因为它们不包含出度极高的顶点，例如Facebook的最大出度是9170。对于其他图，改进幅度超过10%，对于拥有数千个顶点、超过105条边的Kronecker图，改进幅度高达30%到50%。这表明缓存这些中心顶点是非常有益的。

总之,Enterprise提高了BFS算法的TEPS 3.3×至105.5×。最高的TEPS在KR0中达到，超过760亿TEPS；最小的在FR中达到，为31亿TEPS。

比较。图14比较了Enterprise与几种基于GPU的BFS实现，包括B40C[33]、Gunrock[44]、MapGraph[18]和GraphBIG[2]。我们评估了幂律图，如FB、TW和KR-21-128，它有200万个顶点，平均每个顶点的出度为128，以及长直径图，如audikw1[7]、roadCA[6]和europe。osm [7]。

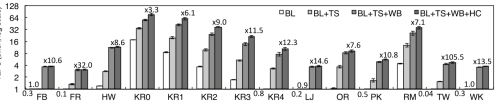
图13:各种图上的Enterprise绩效。在GPU上使用状态数组方法对BFS进行方向优化作为基线(BL)。三种技术分别为用于流线型GPU线程调度的TS、用于工作负载平衡的WB和用于中心顶点缓存的HC。

对于幂律图,Enterprise分别比B40C ，Gunrock， MapGraph和Graph-BIG快4×，5×，9×，74x。对于长直径图,Enterprise平均达到14.1亿TEPS，优于Gun-rock (0.72) 1.95×，优于MapGraph (0.25) 5.56×，优于GraphBIG 42×(0.03)。在这些图中，Enterprise交付的性能类似于B40C。它在europe.osm上的运行速度略慢，因为这个图的出度很小，最大的出度是12，平均值是2.1。

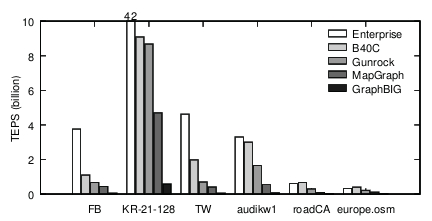
图14:性能比较

5.2Enterprise的可扩展性

图15显示了Enterprise的强可扩展性和弱可扩展性。我们使用表1中最大的图，即KR4，测试强可扩展性。在2、4和8个gpu上，Enterprise分别实现了150、180和184亿TEPS，即加速43%、71%和75%。

我们用两种方法来评估弱可扩展性，边尺度和顶点尺度。当GPU数增加时，我们固定顶点数同时增加边因子——平均出度，或者使用固定平均出度数同时增加顶点的数量。如图15所示,我们在边尺度上获得更好的可扩展性,我们获得超线性加速,也就是说,9.1×，960亿TEPS在 8 GPU上。这是因为当edgeFactor增加时，图中中心顶点的数量也会增加，中心顶点缓存将减少更多的全局内存访问。另一方面，方向切换可以避免更多不必要的边缘检查。

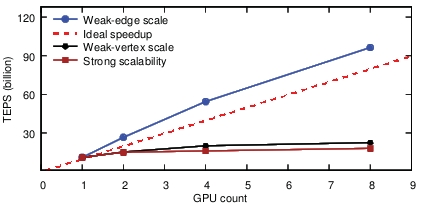
图15:Enterprise的强可伸缩性和弱可伸缩性。

5.3 GPU计数器分析

由于BFS是一种I/ o密集型算法，因此GPU线程能够快速访问数据至关重要。如图16(a)所示，我们的前沿技术(TS和WB)显著提高了GPU读取/存储功能单元的利用率，平均分别提高了8%和24%，最高可达68%。此外，我们的中心顶点缓存(HC)如图16(b)所示，减少了40%的数据请求延迟，此类事件的发生率从4.8%下降到2.9%。这也解释了图16(c)中在GPU上观察到的IPC的两倍。

为了便于比较，我们还在Hollywood graph上对[33]进行了描述，在该图传输效率为27亿TEPS，消耗40瓦功率，实现了40%的负载/存储单元利用率和0.68 IPC。在同一图中，Enterprise实现了50%的负荷/存储单元利用率和1.32 IPC，拥有120亿TEPS的效率和76瓦的功耗。

图16(d)为不同技术对应的GPU功耗图。这里我们只报告GPU的功率来了解每种技术的能力。在我们的GPU线程调度下，平均功耗从86瓦下降到81瓦，最大的节省在Twitter图上，是14.5瓦。这主要来自系统中更好的IO性能和更少的空闲GPU线程。另外两种技术(WB和HC)进一步将功率降低到78瓦。

6. 相关工作

我们的系统Enterprise在图遍历的设计和实现方面处于领先水平。先前的工作要么使用前沿队列[30,33]，要么使用状态数组[24]。即使一起使用这两种数据结构时，现有的解决方案也是在不同的地方使用它们，例如，[36,29]在扩展阶段使用状态数组和在其他阶段使用前沿队列方法，[10]以及在自上而下方法中使用前沿队列，自下而上方法中使用状态数组。Enterprise自始至终都在同时使用这两种数据结构，并在GPU上提供了前所未有的性能。

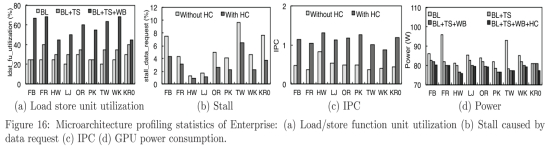
图16.Enterprise的微结构的统计数据（a）加载/存储功能单元利用率（b）由数据请求引起的停顿（c）IPC（d）GPU功耗。

最近提出了几种用于GPU的工作负载平衡技术，如任务窃取[15,12]和工作负载捐赠[41,14]。然而，这种类型的技术通常只在一小部分线程中使用，在我们的工作中，对数千个线程之间进行协调是极具挑战性的。相反，Enterprise瞄准BFS工作负载不平衡的根源，并对不同的边界进点行分类，以减轻问题。

有许多项目[39,20,38]利用中心顶点来减少通信开销，特别是在分布式BFS中。例如，[39]在每一层复制所有机器上的中心顶点的状态，[20]和[38]将中心顶点划分为多个分区，并以基于树的方式进行通信。相比之下，当围绕中心顶点展开和检查时，Enterprise只支持自底向上阶段的中心顶点缓存。此外，由于GPU共享内存是有限的，Enterprise在每一层都使用在下一层最有可能访问的对象更新缓存。

功率效率[45]对于系统设计非常重要，如[43]提前关闭GPU流处理器以节省功率。我们的工作表明，基于GPU 的图算法在提供高性能和高能效方面具有巨大的潜力。

7. 结论

在这项工作中，我们开发了一个新的基于GPU的BFS系统Enterprise，该系统在一个GPU上可以产生超过700亿TEPS，在两个GPU上可以产生1220亿TEPS，可以达到4.46亿TEPS/瓦。这是通过高效管理众多的GPU流处理器和独特的内存层次来实现的。作为未来工作的一部分，我们计划将Enterprise与高速存储和网络设备集成，并在更大的图上运行。

致谢

我们感谢匿名审稿人的有益建议。我们也要感谢英伟达的学术合作奖和硬件捐赠。本材料基于部分由国家科学基金会职业奖CNS-1350766和奖助金IOS-1124813支持的研究。

8. 参考文献

[1]Graph500. http://www.graph500.org/.

[2]GraphBIG. https://github.com/graphbig.

[3]GTgraph: A suite of synthetic random graph generators. http://www.cse.psu.edu/~madduri/software/GTgraph/.

[4]NVIDIA Corporation: CUDA C Programming Guide.

[5]NVIDIA Profiler Tools. http://docs.nvidia.com/cuda/profiler-users-guide/.

[6]SNAP: Stanford Large Network Dataset Collection. http://snap.stanford.edu/data/.

[7]The University of Florida: Sparse Matrix Collection. http://www.cise.ufl.edu/research/sparse/matrices/.

[8]NVIDIA Corporation: Kepler GK110 Architecture Whitepaper. 2013.

[9]R. Albert, H. Jeong, and A.-L. Barab´asi. Internet: Diameter of the World-Wide Web. Nature, 401(6749):130–131, 1999.

[10]S. Beamer, K. Asanovi´c, and D. Patterson. Direction-Optimizing Freadth-First Search. In Proceedings of the Conference on High Performance Computing, Networking, Storage and Analysis (SC), 2012.

[11]E. G. Boman, K. D. Devine, and S. Rajamanickam. Scalable Matrix Computations on Large Scale-Free Graphs Using 2D Graph Partitioning. In Proceedings of the Conference on High Performance Computing, Networking, Storage and Analysis (SC), 2013.

[12]D. Cederman and P. Tsigas. On Dynamic Load Balancing on Graphics Processors. In Proceedings of the SIGGRAPH/EUROGRAPHICS Symposium on Graphics Hardware, pages 57–64. Eurographics Association, 2008.

[13]D. Chakrabarti, Y. Zhan, and C. Faloutsos. R-MAT: A Recursive Model for Graph Mining. In SDM, volume 4, pages 442–446. SIAM, 2004.

[14]A. Cohen, T. Grosser, P. H. Kelly, J. Ramanujam, P. Sadayappan, and S. Verdoolaege. Split Tiling for GPUs: Automatic Parallelization Using Trapezoidal Tiles to Reconcile Parallelism and Locality, avoiding Divergence and Load Imbalance. In Proceedings of Workshop on General Purpose Processing Using GPUs (GPGPU), 2013.

[15]J. Dinan, D. B. Larkins, P. Sadayappan, S. Krishnamoorthy, and J. Nieplocha. Scalable Work Stealing. In Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis (SC), 2009.

[16]S. Dolev, Y. Elovici, and R. Puzis. Routing Betweenness Centrality. Journal of the ACM (JACM), 57(4):25, 2010.

[17]D. Easley and J. Kleinberg. Networks, Crowds, and Markets: Reasoning About A Highly Connected World. Cambridge University Press, 2010.

[18]Z. Fu, M. Personick, and B. Thompson. MapGraph: A High Level API for Fast Development of High Performance Graph Analytics on GPUs. In Proceedings of Workshop on GRAph Data management Experiences and Systems (GRADES), 2014.

[19]M. Gjoka, M. Kurant, C. T. Butts, and A. Markopoulou. Practical Recommendations on Crawling Online Social Networks. Journal on Selected Areas in Communications, 29(9):1872–1892, 2011.

[20]J. E. Gonzalez, Y. Low, H. Gu, D. Bickson, and C. Guestrin. PowerGraph: Distributed Graph-Parallel Computation on Natural Graphs. In Proceedings of USENIX conference on Operating Systems Design and Implementation (OSDI), 2012.

[21]P. Harish and P. Narayanan. Accelerating Large Graph Algorithms on the GPU using CUDA. In High Performance Computing (HiPC). Springer, 2007.

[22]M. Harris, S. Sengupta, and J. D. Owens. Parallel Prefix Sum (Scan) with CUDA. GPU gems, 2007.

[23]S. Hong, S. K. Kim, T. Oguntebi, and K. Olukotun. Accelerating CUDA Graph Algorithms at Maximum Warp. In Proceedings of SIGPLAN Symposium on Principles and Practice of Parallel Programming (PPoPP), 2011.

[24]S. Hong, T. Oguntebi, and K. Olukotun. Efficient Parallel Graph Exploration on Multi-Core CPU and GPU. In Proceeding of the Conference on Parallel Architectures and Compilation Techniques (PACT), 2011.

[25]B. A. Huberman and L. A. Adamic. Internet: Growth Dynamics of the World-Wide Web. Nature, 401(6749):131–131, 1999.

[26]H. Jeong, B. Tombor, R. Albert, Z. N. Oltvai, and A.-L. Barab´asi. The Large-scale Organization of Metabolic Networks. Nature, 407(6804):651–654, 2000.

[27]H. Kwak, C. Lee, H. Park, and S. Moon. What is Twitter, A Social Network or A News Media? In Proceedings of International Conference on World Wide Web (WWW), 2010.

[28]D. Levinthal. Performance Analysis Guide for Intel Core i7 Processor and Intel Xeon 5500 Processors. Intel Performance Analysis Guide, 2009.

[29]D. Li and M. Becchi. Deploying Graph Algorithms on GPUs: An Adaptive Solution. In International Symposium on Parallel & Distributed Processing (IPDPS), 2013.

[30]L. Luo, M. Wong, and W.-m. Hwu. An Effective GPU Implementation of Breadth-First Search. In Proceedings of Design Automation Conference (DAC), 2010.

[31]K. Madduri, D. Ediger, K. Jiang, D. A. Bader, and D. Chavarria-Miranda. A Faster Parallel Algorithm and Efficient Multithreaded Implementations for Evaluating Betweenness Centrality on Massive Datasets. In International Symposium on Parallel & Distributed Processing (IPDPS), 2009.

[32]A. McLaughlin and D. A. Bader. Scalable and High Performance Betweenness Centrality on the GPU. In Proceedings of the Conference on High Performance Computing, Networking, Storage and Analysis (SC), 2014.

[33]D. Merrill, M. Garland, and A. Grimshaw. Scalable GPU Graph Traversal. In Proceedings of SIGPLAN Symposium on Principles and Practice of Parallel Programming (PPoPP), 2012.

[34]D. Merrill and A. Grimshaw. Parallel Scan for Stream Architectures. Technical report, University of Virginia, 2009.

[35]R. Nasre, M. Burtscher, and K. Pingali. Atomic-Free Irregular Computations on GPUs. In Proceedings of Workshop on General Purpose Processor Using GPUs (GPGPU), 2013.

[36]R. Nasre, M. Burtscher, and K. Pingali. Data-Driven Versus Topology-Driven Irregular Computations on GPUs. In International Symposium on Parallel & Distributed Processing (IPDPS), 2013.

[37]P. W. Olsen, A. G. Labouseur, and J.-H. Hwang. Efficient Top-k Closeness Centrality Search. In International Conference on Data Engineering (ICDE), 2014.

[38]R. Pearce, M. Gokhale, and N. M. Amato. Scaling Techniques for Massive Scale-Free Graphs in Distributed (External) Memory. In International Symposium on Parallel & Distributed Processing (IPDPS), 2013.

[39]Z. Qi, Y. Xiao, B. Shao, and H. Wang. Toward a Distance Oracle for Billion-Node Graphs. Proceedings of the VLDB Endowment, 7(1):61–72, 2013.

[40]A. E. Sarıy¨uce, E. Saule, K. Kaya, and ¨U. V. Cataly¨urek. Regularizing Graph Centrality Computations. Journal of Parallel and Distributed Computing, 2014.

[41]S. Tzeng, A. Patney, and J. D. Owens. Task Management for Irregular-Parallel Workloads on the GPU. In Proceedings of the Conference on High Performance Graphics, 2010.

[42]V. Ufimtsev and S. Bhowmick. Application of Group Testing in Identifying High Betweenness Centrality Vertices in Complex Networks. In Workshop on Machine Learning with Graphs, KDD, 2013.

[43]P.-H. Wang, Y.-M. Chen, C.-L. Yang, and Y.-J. Cheng. A Predictive Shutdown Technique for GPU Shader Processors. Computer Architecture Letters, 2009.

[44]Y. Wang, A. Davidson, Y. Pan, Y. Wu, A. Riffel, and J. D. Owens. Gunrock: A High-Performance Graph Processing Library on the GPU. In Proceedings of SIGPLAN Symposium on Principles and Practice of Parallel Programming (PPoPP), 2015.

  全套毕业设计论文现成成品资料请咨询微信号：biyezuopin QQ：2922748026     返回首页 如转载请注明来源于www.biyezuopin.vip