目录
一、实验目的及要求
二、算法原理概述
1、图的基本概念
2、最短路径(Prim算法和Dijkstra算法)
3、拓扑排序
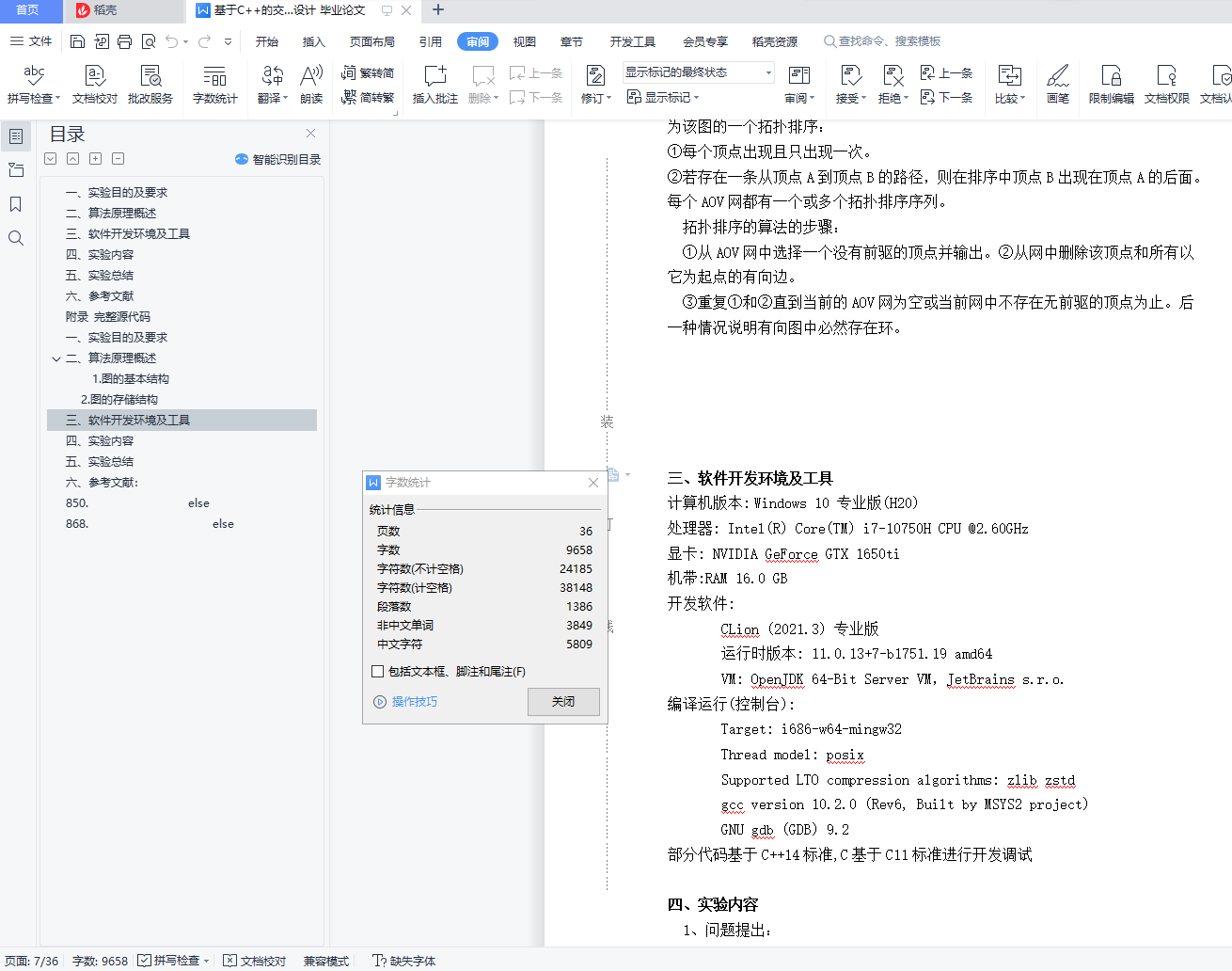
三、软件开发环境及工具
四、实验内容
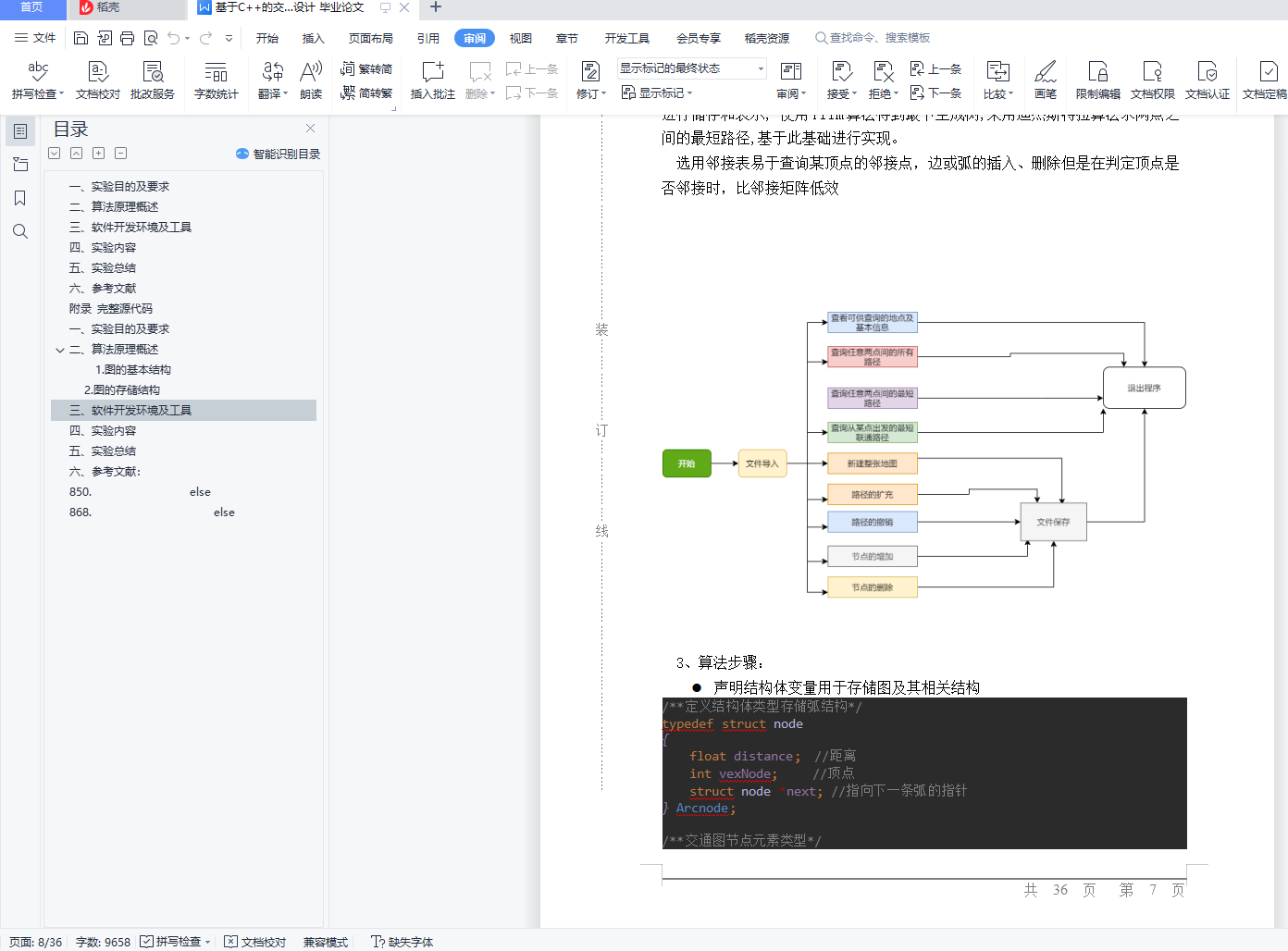
1、问题提出
2、解决思路
3、算法步骤
4、结果分析
5、实验核心代码
五、实验总结
六、参考文献
附录 完整源代码
一、实验目的及要求
（1）图的存储表示及其基本操作实现。
（2）最短路径算法。
（3）系统功能：要求设计一个简易的交通咨询系统，可让用户咨询任意两
个城市之间的最短距离、最低花费或最少时间等问题。
（4）对于不同的咨询要求，输入咨询的内容。
（5）用户界面的友好性：程序能提供菜单供用户选择以及相应的交互信息。
二、算法原理概述
  1.图的基本结构
（1）有向图。若E是有向边（弧）的有限集合时，则图G为有向图。弧是顶点的有序对，记为<v，w>，其中v，w是顶点，v称为弧尾，w称为弧头，<v，w>称为从顶点v到顶点w的弧。
（2）无向图。若E是无向边（边）的有限集合时，则图G为无向图。边是顶点的无序对，记为（v，w）或（w，v），因为两者相等，其中v，w是顶点，顶点V，w互为邻接点。边（v，w）依附于顶点v，w，或者边（v，W）和顶点v，w相关联。
（3）简单图。一个图G若满足：①不存在重复边；②不存在顶点到自身的边，则称图G为简单图。
（4）多重图。若图G中某两个结点之间的边数多于一条，又允许顶点通过一条边和自己关联，则图G为多重图。
（5）完全图（筒单完全图）。对于无向图，任意两个顶点之间都存在边。
对于有向图，任意两个顶点之间都存在方向相反的两条弧。
（6）子图。设有两个图G=（V，E）和G'=（V，E），若”是V的子集，且E'是E的子集，则称G'是G的子图。若有满足V（G）=V（G）的子图G，则称其为G的生成子图。
（7）连通、连通图。
在无向图中，若从顶点v到顶点w有路径存在，则称v和w是连通的。
若图G中任意两个顶点都是连通的，则称图G是连通图。极小连通子图是既要保持图连通又要使得边数最少的子图。
（8）生成树。连通图的生成树是包含图中全部顶点的一个极小连通子图。
（9）顶点的度、入度和出度。
对于无向图，顶点v是依附于该顶点的边的条数。无向图的全部顶点的度的和等于边数的两倍。
对于有向图，入度是以顶点v为终点的有向边的数目。出度是以顶点v为起点的有向边的数目。顶点的度等于入度和出度之和。有向图的全部顶点的入度之和与出度之和相等，并且等于边数。
（10）边的权和网。在一个图中，每条边都可以标上具有某种意义的数值，该数值称为该边的权值。这种边上带有权值的图称为带权图，也称网。
2.图的存储结构
图的存储结构有四种：邻接矩阵法、邻接表法、十字链表法、邻接多重表法。（11）路径、路径长度和回路。
顶点v。到顶点v，之间的一条路径是指顶点序列Ve，V1，Ve…，Vm，Ve。
路径上边的数目称为路径长度。第一个顶点和最后一个顶点相同的路径称为回路或环。