|
1. 毕业设计(论文)综述(题目背景、研究意义及国内外相关研究情况)
1.1选题背景及意义
共轭梯度法因无需计算和存储目标函数的Hesse矩阵,而具有易操作、速度快、存储小等特点,使其成为求解大规模无约束优化问题的有效工具,并广泛应用于求解大型稀疏线性系统、地震图像数据的拟合、压缩感知等实际问题。非线性优化是运筹学与计算数学的交叉学科。许多实际问题如国防、石油勘探、天气预报、管理、金融学等一些问题都可归纳为非线性优化问题.例如信息科学中的模式识别问题、金融学中的投资组合问题、地球科学中的反演问题等。这些实际问题通常都是高维度的非线性问题,所以研究高效的求解非线性优化问题的方法具有十分重要的意义。
1.2国内外相关研究情况
共轭梯度法最早是由计算数学家Hestenes和几何学家Stiefel在20世纪50年代初为求解线性方程组

而独立提出的。他们奠定了共轭梯度法的基础,他们的文章详细讨论了求解线性方程组的共轭梯度法的性质以及它和其他方法的关系。当 对称正定时,上述线性方程组等价于最优化问题 对称正定时,上述线性方程组等价于最优化问题

基于此,Hestenes和Stiefel的方法可视为求解二次函数极小值的共轭梯度法。1964年,Fletcher和Reevse将此方法推广到非线性优化,得到了求一般函数极小值的共轭梯度法。
而本书中,戴彧虹和袁亚湘介绍了多种类型的共轭梯度法,各方法的区分主要在于每次迭代的方向上,并且他们检验了每种方法在不同搜索下的全局收敛性。在他们的研究中,目标函数连续可微有下界,导数满足Lipschitz条件,他们通过对Zoutendijk条件的判断,通常用反证的方法来考察全局各共轭梯度法的全局收敛性问题。
对于无约束优化问题
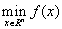
一般给出一初值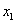 ,经由算法迭代产生 ,经由算法迭代产生 。在第k次迭代,当前迭代点为 。在第k次迭代,当前迭代点为 ,用一种方法产生一搜索方向 ,用一种方法产生一搜索方向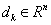 。然后下一迭代点为: 。然后下一迭代点为:
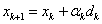
其中,迭代方向 的不同选取产生了不同的共轭梯度法, 的不同选取产生了不同的共轭梯度法,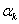 为步长因子,步长的不同选取产生了不同的搜索准则。而本书着重研究各方法在精确线搜索,Curry原则,强Wolfe线搜索和推广的Wolfe线搜索下的收敛性。其中: 为步长因子,步长的不同选取产生了不同的搜索准则。而本书着重研究各方法在精确线搜索,Curry原则,强Wolfe线搜索和推广的Wolfe线搜索下的收敛性。其中:
精确线搜索要求每次迭代的步长满足:
Curry原则要求每次迭代的步长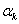 为一维函数 为一维函数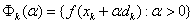 的第一个极小点。 的第一个极小点。
强Wolfe线搜索要求每次迭代的步长满足:

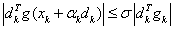
其中,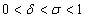 。 。
推广的Wolfe线搜索要求每次迭代的步长满足:


其中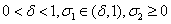 。 。
而迭代方向一般为:
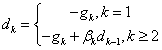
可知迭代方向的不同由 产生,故 产生,故 的不同选取产生的各种共轭梯度法,戴彧虹和袁亚湘介绍了如下方法,有: 的不同选取产生的各种共轭梯度法,戴彧虹和袁亚湘介绍了如下方法,有:
Fletcher和Reeves在1964年求解线性方程组推广而得的共轭梯度法,简称FR方法。
Polak和Ribiere和Polyak在1969年独立提出的一种非线性共轭梯度法,简称PRP方法。Hestenes和Stiefel给出的另一种HS方法。
Fletcher在1987年引入的共轭下降法,简称为CD方法。戴彧虹和袁亚湘在1995年提出的新的共轭梯度法,简称为DY方法。本书中给出了各种方法在不同搜索标准下的收敛性条件和全局收敛证明。
2. 本课题研究的主要内容和拟采用的研究方案、研究方法或措施
2.1研究主要内容
本文拟对共轭梯度法中搜索方向的迭代参数进行改进,并基于新公式给出算法框架。证明由算法框架产生的迭代方向均满足充分下降条件,且在适当条件下证明算法的全局收敛性;最后,对新算法进行数值测试,以验证方法的有效性。
2.2研究方案
第一,首先给出本文研究课题的现实背景,其次给出共扼梯度法的发展历程,最后给出本文的结构安排。
第二,首先介绍无约束优化问题的一些基础理论知识,包括无约束问题的最优解的判断条件等;之后介绍方程组怎样转化成无约束问题进行求解;最后介绍一些常用的线搜索及搜索方向的技术。
第三,采用一种改进的三项共扼梯度法结合投影技术求解非线性方程组问题,且在满足适当的假设条件下,证明该算法具有充分下降性和全局收敛性。最后通过数值实验说明该算法的有效性。
第四,采用改进的HZ共扼梯度法结合投影技术求解非线性方程组问题,且在满足适当的假设条件下,证明该算法具有充分下降性和全局收敛性。最后通过数值实验说明该算法能较好的求解此类非线性方程组问题。
2.3研究方法或措施
本文通过改进的共辘梯度算法,结合投影技术,将方程组问题转化为无约束问题后进行求解,并在一定的条件下证明了算法的充分下降性、自动信赖域性质以及全局收敛性。
3. 本课题研究的重点及难点,前期已开展工作
3.1重点
对于非线性方程组问题,本文修正一个新的搜索方向。在适当的假设条件下证明其充分下降性和全局收敛性。通过数值实验中,证明本文所设计的算法NN的数值结果优于算法PRP。
3.2难点
对新算法进行数值测试,以验证方法的有效性。通过数值实验,并在与原算法的比较中,证明数值结果更好。
3.3前期已开展工作
目前已经结合任务要求,掌握了一些关于无约束优化问题的基本定义,以及最优解的判断条件等;熟悉了一些转换手段,和一些线搜索技术。
4. 完成本课题的工作方案及进度计划(按周次填写)
第1周—第2周 查阅资料,熟悉共轭梯度算法步骤及基本理论;
第3周—第8周 查阅资料,对基本的共轭梯度算法进行改进并上机实现,撰写提纲;
第9周—第13周 着手写论文,师生讨论相关问题,完成初稿;
第14周—第16周 修改论文;
第17周—第18周 定稿,准备答辩。
|



