带有光学感应器的非圆轮磨的过程控制
摘要:圆柱形磨床(CGM)正越来越多地用于生产非圆零件的轮廓。这意味着新的需求来进行生产过程监控和全过程测量以生产这些非圆轮廓。一个新的光学传感器系统集成到这样一个研磨机,使得它可以通过测量来保证质量,研磨过程的最佳化和减少建立和加工的时间。
关键词:过程测量,光学,磨床
1简介
圆柱形磨床遭受各种干扰,如刀具磨损、温度漂移、轨迹控制偏差等。这导致生产率下降和工件尺寸偏差。多种监测量具可以帮助提高研磨过程[1]。测量控制程序可以用于补偿大多数外圆磨削中的干扰。这得益于在磨削过程中的自动测量和定位工具。测量头采用触碰探头。现在这些测量控制被广泛使用并且稳固建立; 在高精度加工中,他们对高效率、稳固制造工艺是必要。可以预料,智能监测磨削过程中发挥着越来越重要的作用[2]。大多数的触碰探头只用于坐标测量机床(CMMs) [3];他们中的一些也适用于工作母机。
今天的现代化圆柱形磨床还可以用于高精度磨削加工非圆轮廓。为此,圆柱形磨床在X轴和C轴的轨迹控制中被持续使用,例如偏心磨削。测量头当受剪切力时受破坏而不能工作 [4]。由于在非圆磨削中不能测量,这一新技术的巨大潜力不能充分利用了。
当使用非接触式测量头,没有剪切力。为此,他们在圆磨机床中尤其可用[5]。很长一段时间,高要求,不利的环境条件阻碍了光传感器在圆柱形磨床中的使用。这就是为什么光学测试原理能够测量不同的材料而被用于非圆磨床。
2机器概念和光学传感器
距离测量传感器被安装在磨床轮上的头部(图1)。作为替代磨轮的头部,它可以实现自动测量,否则它将被放在机床的背部。圆柱形磨床的测量原理的选择标准是[6]静态测试,例如,重复性,局部再生性、操上的重复能力/测量范围等。斜度极限, 举例来说,点对点的范围内的探测误差。动态测试,例如,扫描探测误差等遵照以下各种测试,彩色共焦距离传感器[7]被选作测量头。该传感器采用多色点信号源。由于彩色偏差的使用,每一个焦点,或传感器和工件表面之间的距离,相当于一个特定的波长。
分光仪用于测量反射光的波长。这种测量原理比其他测量原理最重要的优点是它不受不同表面的影响,它也适合于光滑的表面。由于传感器被安装在磨轮的头部,它像磨轮一样沿x轴移动。在高精度测量中,它仅需要一个为1毫米的小的测量范围就可测量一个大的工作距离。测量头上x轴(增量线编码器)与传感器信号之间的同步性增加了测量范围并且可以测量的整个x轴。
3设计和功能
光学传感器是完全集成在圆柱形磨床数控单元中。这允许来自传感器、X 轴、C 轴 和Z轴的信息能够同时地被记录和连接。为了方便检验,
基于单个元件与坐标变换之间的通信,对整个系统进行设计,这个系统作为一个模拟装置被开发和使用(图2)。有了这个模拟器,它就能变得可见并且可以测试圆柱形磨床中传感器的不同分布,类似于一个三维CAD系统。此外,不同的工件轮廓可以被测量并且,虚拟的测量结果能被显示出来。
模拟器也可以用来开发校对规程和检查测量功能。校准程序被用来确定圆柱形磨床中传感器的位置与方向。这个信息被储存在系统中,使它可以在高精度要求下连接来自传感器的距离信息和圆柱形磨床各轴的位置信息。这个校准过程可以通过偏心盘来实现(图3)。
这个偏心盘作为校准工具,被安装在圆柱形磨床中并且被测量头测量。使用偏心盘做校准器的好处是在磨床中偏心盘本身就易于校准和测量。所有为传感器的位置和方向设置的三个变量可以通过一次测量中严谨的数据来确定。如果安装是最优的话,测量时会产生一个正弦信号。如果传感器的位置和方向不理想,就会产生偏离的正弦信号。传感器和工件之间的距离 (△t)、测量轴和旋转轴之间的垂直 距离 (△s)和传感器的偏移角(△u)全显示在传感器坐标系统---图3中。它们都可以通过这些偏差来确定。测量系统包括以下功能(图4);
·C角测量
·直径测量
·轮廓测量
在非圆工件的高精度磨削时,圆柱形磨床中工件方向的确定(C-angle) 能降低调定时间。直径和剖面的确定能优化磨削过程并且确保工件的质量。应该指出的是只有未进行机械加工的零件的测量是有价值的,因为在机加工工件的公差被广泛应用的今天系统不能足够精确地工作。
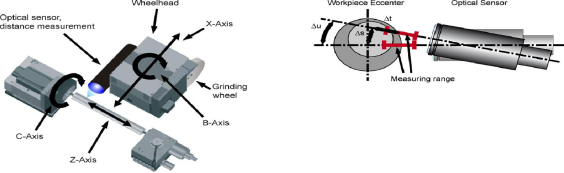
图3。带有偏心盘工具的测量系统校对。
图1 .磨床上轮盘头部光学传感器的分布
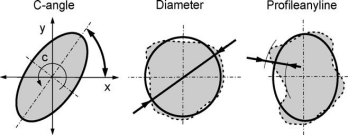
图4。系统的测量功能
光学距离传感器能够实现的根据是大量的测量原理[8]。每一个测量原理都有其优缺点。当设计测量系统时就要把他们考虑在内;它的设计是符合光学传感器接口规范的OSIS)[9],这个规范使它更容易替代来自不同厂家的传感器并且能使用不同的测量原理
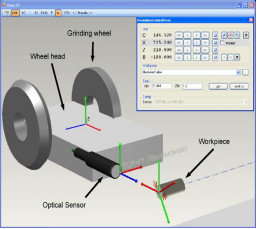

图2。配置模拟器,坐标变换和测试。图5。泵部件、典型测量任务
表1不确定性因素
|
不确定性因素
|
直径(mm)
|
C-角(°)
|
剖面(um)
|
|
重复性,ur
|
0.1
|
0.003
|
0.4
|
|
传感器线性度, ulin_s
|
0.2
|
–
|
0.2
|
|
轴线性, ulin_CGM
|
0.2
|
0.001
|
0.2
|
|
垂直度 ,Z up
|
0.7
|
–
|
0.3
|
|
温度 ,u
|
2.1
|
–
|
1.1
|
|
校准 u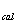
|
0.3
|
0.005
|
1.0
|
|
偏差,Dsys
|
0.4
|
0.005
|
0.9
|
|
结合标准不确定度, uc
|
2.3
|
0.006
|
1.6
|
|
扩展不确定度(k = 2) ,U
|
5
|
0.02
|
4
|
4实验性和结果
4.1 典型工件作测试品
测量不确定度总是依据测量任务 [10]。因为这个原因,在1999年以前一个典型的测量任务被定义并且以细化为精确的测量过程为标准[11]来比较3维坐标测量机械德效率。直到磨床被关注标准才开始变得先进。使用磨床时为了估计测量头的效率, 一个典型工件——泵部件(图5)的具体测量任务被确定了。
4.2。测量不确定性项
这些任务的测量不确定性项可以被确定。列在表1中的主要因素被考虑在内。个别的主要因素通过测试的方法被确定式确定。重复性的实验用以确定重复性(u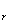 )。该测量数据也用来确定系统偏差(D
)。该测量数据也用来确定系统偏差(D )。圆柱形磨床轴(u
)。圆柱形磨床轴(u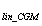 )线性度和传感器线性度(u
)线性度和传感器线性度(u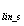 )来自制造商的规范。圆柱形磨床Z轴的垂直度能手动调节。被圆柱形磨床使用者使用的典型的垂直度通过实验确定;它被看做标准不确定度值。温度引起工件的热膨胀和整个磨床的变形。圆柱形磨床不是冷却的。周围环境波动1 8 ℃。为评估温度的效果,位置测量在经过较长一段时间后使用激光干涉仪。这个数据被用来确定温度效应(u
)来自制造商的规范。圆柱形磨床Z轴的垂直度能手动调节。被圆柱形磨床使用者使用的典型的垂直度通过实验确定;它被看做标准不确定度值。温度引起工件的热膨胀和整个磨床的变形。圆柱形磨床不是冷却的。周围环境波动1 8 ℃。为评估温度的效果,位置测量在经过较长一段时间后使用激光干涉仪。这个数据被用来确定温度效应(u ) ,在两个程序之间三十分钟被观察到校准间隔。工件在磨床上加工并且反馈给高精度坐标测量机械(u
) ,在两个程序之间三十分钟被观察到校准间隔。工件在磨床上加工并且反馈给高精度坐标测量机械(u ),这个工件就用作实验。个别主要因素与误差累加定律的延伸 (1)和计算不确定性(2)的扩展集合在一起。
),这个工件就用作实验。个别主要因素与误差累加定律的延伸 (1)和计算不确定性(2)的扩展集合在一起。
公式1.2

 ︱D
︱D ︱
︱
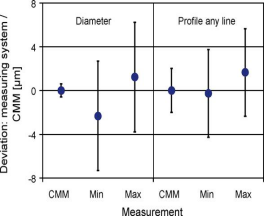

图6 集成光学传感器和工件的圆柱磨床。 图7 .测量系统的测量结果和坐标测量机械的比
4.3实验结果
整个传感器系统整合在一个高精度磨床[12]并且在制造商的实验性的研磨车间被测试 (图6)。采用各种测试计算测量头和效率的测量头和整个系统的效率(圆柱形磨床和传感器)。外圆磨床量方法和高精度坐标测量机床的测量法方法形成对比。3毫米到47毫米之间的尺寸规格的测量方法已经实行。一个最大半径22毫米最小半径17毫米的与椭圆形非圆轮廓轮也已经实施。尺寸的直径误差控制在0.5毫米内。测量头和坐标测量机床的测量尺寸 - 直径误差D在D =2.3毫米和D = + 1.2毫米之间。外圆磨床的剖面测量尺寸和那些在坐标测量机械的测量尺寸的不同是它在P =0.3毫米P = + 1.6毫米之间。图7表示了在直径测量和剖面测量中的极值; 此外,这些特征的测量不确定性同时被给出。
在这个新的测量系统中,这种不确定性在直径和剖面的测量范围内。这种不确定性不仅和坐标测量机床的不确定度范围相重叠而且还包括它。因此,这些实验测量方法确定了假设和计算的不确定项(表1)。
5结论
综上所述在磨床中使用光学传感器用以磨削非圆轮廓是可能并且有用的,尽管它不能在磨削过程中直接测得。为磨床的磨削间歇之前或期间的测量提供许多便利。利用监控磨削过程的新方法,这种计量方法在整个制造过程中产生了附加值。它成为有益的计量方法[13]。它不仅能够检测轮廓误而且能报废公差之外的工件。它也能获得来自测量结果的关于磨削工艺的新的信息和知识并且通过优化输入速率和转速用以交流和提高工艺。即使知道圆柱形磨床动力的限制可以提高的。例如,非圆轮廓的磨削能引起高加速度,这种加速度在轨迹控制中能引起极大地破坏。磨削后的轮廓测量能够检测超调量,这种超调量可以通过优化路径控制参数降低。
在测量工件直径中测量不确定度的程度足测量工件的瑕疵。相对位置的确定利用UC-angle = 0.028 (k = 2)是非常不错的方法。这意味着准备时间和加工时间可以缩短。此外, 当用磨床测量剖面时在微米范围内的测量不确定度可以实现,这时的磨床具有更高的精度,只能用高精度坐标测量机床来实现。这里的工件要被释放也许需要能重新被抓取定位。这通常非常费时并且高精度要求的抓取通常是不可能的。
目前测量头处在雏形阶段。不确定性因素的相当大的比例是由于磨床上的温度漂移造成的。此外,校准过程的工件和它的可描述性性扮演一个重要的角色。系统偏差受到进一步地研究。
该传感器不能区别工件的表面和冷却液的表面。这导致系统偏差在1毫米和4毫米之间,依靠冷却薄膜。因为这种重要因素在减少或补偿方面进一步的研究正在进行。
近些年,光学传感器领域已经取得巨大进步。其他的物理效应和组合测量已知的原则,将用于新的传感器系统。接口标准化将使新的光学距离传感器被整合,这里的风险和过程是可计算的并且浪费时间越来越少[14]。
鸣谢
作者要感谢CTI, 联邦政府部门的经济事务驻瑞士创新促进会在财政上的支持。
参考文献:
(1)To¨nshoff HK, Friemuth T, Becker JC (2002) Process Monitoring in Grinding.
Annals of the CIRP 51(2):551–571.
(2)Inasaki I, To¨nshoff HK, Howes TD (1993) Abrasive Machining in the Future.
Annals of the CIRP 42(2):723–731.
(3)Weckenmann A, Estler T, Peggs G, McMurtry D (2004) Probing Systems in Dimensional Metrology. Annals of the CIRP 53(2):657–684.
(4)Patzig C (2002) Maschinenintegrierte Post-process Form-Messung beim CNC-Unrundschleifen (Machine Integrated Post-process Form Measurement in CNC Noncircular Grinding), Dissertation (PhD), Technische Universita¨t Graz.
(5)Schwenke H, Neuschaefer-Rube U, Pfeifer T, Kunzmann H (2002) Optical Methods for Dimensional Metrology in Production Engineering. Annals of the CIRP 51(2):679–685.
(6) http://www.ntb.ch/files/1/4013/Vortrag_OSIS_Control_2005_englisch_Inter- net.pdf [accessed 08.03.08].
(7)Neuschaefer-Rube U. (2005) Sensoren und Gera¨teprinzipien fu¨r kleine Merkmale, Koordinatenmesstechnik (Principle of Sensors and Devices for Small Features). Koordinatenmesstechnik, Braunschweig. [VDI Bericht 1914:225–238].
(8)Keferstein CP, Ritter M, Honegger D (2006) Marktanalyse optischer 1D-, 2D-, 3D-Sensoren und optischer KMG (Market Analysis 1D–3D Optical Sensors and Optical Coordinate Measuring Machines). Qualitat und Zuverlassigkeit 8:40–41.
(9)Keferstein CP, Zu¨st R (2004) Minimizing Technical and Financial Risk when Integrating and Applying Optical Sensors for in Process Measurement. IMS International Forum. pp. 475–482, ISBN:88-901168-9-7.
(10)ISO/TS 14253-2 1999: GPS—Inspection by Measurement of Workpieces and Measuring Equipment. Part 2: Guide to the Estimation of Uncertainty in GPS Measurement, in Calibration of Measuring Equipment and in Product Verifi-cation.
(11)ISO 10360-2 2000: GPS—Acceptance Test and Reverification Test for Coordi-nate Measuring Machines (CMM). Part 2: CMMs Used for Measuring Linear Dimensions.
(12)Kunzmann H, Pfeiffer T, Schmitt R, Schwenke H, Weckenmann A (2005) Productive Metrology—Adding Value to Manufacture. Annals of the CIRP 54(2):691–704.
(13)Keferstein CP, Dutschke W (2007) Fertigungsmesstechnik (Dimensional Metrol-ogy). 6th ed. Teubner, Wiesbaden.



