基于EMD方法的风速模型分解

1.前言

经验模态分解EMD方法是由黄锷博士提出的一种信号分析方法[1]。它依据数据自身的时间尺度特征来进行信号分解，无须预先设定任何基函数。EMD 方法在理论上可以应用于任何类型的信号的分解，这种方法能够自适应的把非平稳信号分解成一系列零均值的AMFM信号(调频调幅) 的总和，适合于分析非线性、非平稳信号序列，具有很高的信噪比。所以，EMD方法一经提出就在不同的工程领域得到了迅速有效的应用。

MATLAB是一种具有广泛应用前景、全新的计算机高级编程语言[2，3]。它在自动控制、数字信号处理、通信系统设计与仿真等方面具有很好的应用前景。MATLAB已经成为运筹学、自动控制理论、多元统计、数字信号处理、时间序列分析、动态系统仿真、图像处理等高级课程教学中的必备教学工具。

MATLAB软件为工程计算领域提供了准确、高效的多种功能的工具箱，在信号和图像处理等领域具有无可比拟的优势，具有良好的人机交互界面、计算机图形化显示以及强大的数据处理分析能力。EMD是近年来应用前景比较好的信号处理方法之一。通过MATLAB和EMD的结合[4]，实现良好的人机交互界面、计算机图形化显示以及强大的数据处理分析能力的结合。

2.本课题的研究背景

由于风速和风向具有随机变动的自然特性，导致了风电场和系统进行能量交换时存在随机性，为了减少风电对电网造成的影响，扩大风电在电网中的规模比例，有效利用风能，必须提高风电的可控性和可预知性。对风速进行准确的预测可以有效减轻或避免风电场对电力系统的不利影响，同时提高风电场在电力市场中的竞争力。因此，提前准确预测风速参数就具有了重大的意义。进行风电场风速预测的方法有自回归滑动平均(ARMA)时间序列法[5]、神经网络法[6,7]、经验模式分解（EMD）等。

自回归滑动平均模型(ARMA)是将线性自回归模型(AR)和滑动平均模型(MA)结合起来构成的可以描述平稳随机过程的时间序列模型。风速变化的随机性很强，将多个历史风速数据按时间顺序构成一个时间序列，该时间序列即可由ARMA模型来描述。ARMA模型是有限参数模型，只要确定出有限个参数，模型即完全确定。风速时间序列一般是非平稳随机过程，如果希望用ARMA模型进行建模和预测，首先应该对原始数据进行差分运算，使其变为一个平稳随机过程。ARMA模型是时间序列分析与预测中最为常用的模型，但利用该模型的过程中模型识别是比较困难的。

神经网络法对复杂问题的求解十分有效，用于风速的预测结果的精度取决于网络的训练情况。网络训练的越好，预测精度越高。风速具有随机时序性和高度非线性,对于抽取和逼近非线型函数,神经网络是一种合适的方法,它不依靠专家经验,只利用历史数据,可以从训练过程中通过学习来抽取和逼近隐含的输入输出非线性关系。而风速又具有时序性,所以基于神经网络的时间序列分析方法适合于风速的预测。采用神经网络作预测时，没有一个便于选定最合适的神经网络结构的标准方法，只能花大量时间采用凑试法，从许多次实验中找出“最合适”的一种，以神经网络作预测需要更多数据，也需要用更多机时。

经验模态分解(EMD)法适合于分析非线性、非平稳信号序列，具有很高的信噪比。该方法的关键是经验模式分解，它能使复杂信号分解为有限个本征模函数（IMF)[8]，所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号。EMD依据数据自身的时间尺度特征来进行信号分解, 无须预先设定任何基函数。经验模态分解法与短时傅立叶变换、小波分解等方法相比，这种方法是直观的、直接的、后验的和自适应的，因为基函数是由数据本身所分解得到。由于分解是基于信号序列时间尺度的局部特性，因此具有自适应性。

以上分析了三种风速预测的方法，其中第一种方法的缺点是模型识别比较困难，对于没有这方面专业知识的人来说，很难做出准确的预测；第二种方法主要是通过不断的尝试，花大量的时间进行数据的预测校验；第三种方法不仅能预测非线性和非平稳信号，而且基函数是由数据本身分解得到。在本次课题中，我们主要采用EMD预测方法。

3.本课题基本理论

经验模式分解法是对时间序列进行平稳化处理，其结果是将信号中不同尺度的波动或趋势逐级分解开来, 产生一系列具有不同特征尺度的数据序列, 每一个序列称为一个本征模式函数（Intrinsic  Mode  Function ，IMF），最低频率的IMF分量通常情况下代表原始信号的趋势或均值。通过EMD处理,得到的本征模式函数IMF信号具有如下两个特点[9]:1）极值点(极大值和极小值)数目与跨零点数目相等或最多相差一个；2）由局部极大值构成的上包络和由局部极小值构成的小包络的平均值为零。

EMD分解方法假如一个原始数据序列X(t)的极大值或者极小值数目比上跨零点（或下跨零点）的数目多2个（或者2个以上），则该数据序列就需要进行平稳化处理。采用EMD方法对信号X(t)进行分解的步骤：确定信号的所有的局部极值点，然后用3次样条线将所有的局部极大值点连接起来形成上包络，再用3次样条线将所有的局部极小值点连接起来形成下包络线，上下包络线应该包络所有的数据点。下面对信号X(t)进行分解[10]。上下包络线的平均值为m1(t)，原始信号与m1(t)的差记为h1(t)，那么有：

h1(t)=X(t)- m1(t)                          (1)

特别地，如果m1(t)=0，则h1(t)为X(t)的第一个IMF。

但是一般情况下，第一个IMF分量h1(t)对应的m1(t)不可能满足上下包络线均值为零的条件，因此需要把h1(t)作为新的X(t)，重复(1)式，直到h1(t)满足IMF的两个条件，这时h1(t)就是从原始信号筛选出来的第一个IMF。一般的，h1(t)包含X(t)的高频成分。

将h1(t)从原始信号X(t)中分离出来，得到一个去掉高频成分的信号r1(t)，即：

r1(t)= X(t)- h1(t)                          (2)

将r1(t)作为新的信号，即当做X(t)，重新迭代式子(1)，则可以得到第二个IMF 分量h2(t)。通过不断的迭代式子(1) (2)可以分解出所有的IMF分量。直到第k阶的残余信号rn(t)成为单调函数，不能再筛选出新的IMF分量，则分解结束。最终的残余分量rn(t)为：

rn(t)= rn-1(t)-hn(t)                          (3)

最终，原始信号X(t)可以表示成n个IMF分量和残余分量rn(t)的和，即：

X(t)=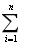hi(t) +rn(t)                       (4)

最终的残留分量rn(t)代表了信号的平均趋势。各IMF分量h1(t)、h2(t)……hn(t)代表了信号从高频到低频的成分，每一个频率所包含的频率分量是不同的。在同一个IMF分量中，不同时刻的瞬时频率也是不一样的，这种频率成分随信号本身的变化而变化。

Huang给出了筛选的偏差标准，即：

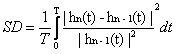                     (5)

当(5)式取值范围为0.2< SD <0.3时，筛选的过程就可以结束了。定义这个标准，主要是为了使hn(t)足够接近IMF的要求，又要控制筛选的次数，在有限多的次数内使所得的IMF分量保留原始信号绝大部分的信息。

由于每一个IMF分量是代表一组特征尺度的数据序列，因此“筛”的过程实际上将原始数据序列分解为各种不同特征波形的叠加，每一个IMF分量既可以是线性的也可以是非线性的。

4.本课题的研究内容

（1）了解EMD的基本原理[11](简述)：1、找到待分解信号的全部极大值和极小值点，利用三次样条函数分别把他们拟合为该信号的上下包络线，计算出两包络线的均值，进而求出待分解信号和均值的差值h(t)；2、若h不满足IMF的要求，则重复上述过程若干次，使得新的h满足IMF的条件；若h满足IMF的要求，则令h为原信号的第1个IMF，并求出原信号与该IMF的差值r(t)；3、将r(t)作为待分解信号，重复以上过程，直到剩余信号rn(t)满足预先给定的终止准则。

（2）详细学习端点处理方法以及包络提取方法[12]：

①极值点提取方法：

对于一个信号非端点处的数据，判断极值点我们用到两种方法。第一种方法：可以通过它与相邻数据的大小关系判断它是否是极值点；如果它同时大于它左右相邻的数据，即为极大值点；如果它同时小于它左右相邻的数据，即为极小值点。对于端点处的数据，例如左端点，如果它大于与它右相邻的那个数据，则它是极大值点。第二种方法：通过求导，在判断该点左右两边的导数符号是否相同，如果不同，即为极值点；否则，不是极值点。

②包络提取方法：

在对信号极值点包络的提取过程中，应用到插值方法。现在应用到的主要插值方法有：a、拉格朗日多项式插值；b、艾尔米特（Hermite）插值；c、三次样条插值等。

（3）使用Matlab编程，实现典型提取方法；

5.总结

经验模式分解法是一种分析非线性、非平稳时间序列的有效方法。对于风速时间序列，利用EMD对其进行平稳化处理，能得到一系列不同频率的平稳分量和趋势项，这些分量能准确地反映原时间序列的局部特征信息和基本趋势。

EMD作为一种新的复杂信号处理方法，自提出以来得到了广泛的认可，在各领域的信号处理方面发挥了很大的作用。Huang提出EMD方法以后，也对EMD进行了一些必要的修改，修补了其中存在的包络线拟合和端点问题。

一般我们采用插值方法提取包络线，通过EMD和MATLAB的结合，实现简单的包络线提取。MATLAB多样化的工具、人机交互界面和强大的数据处理能力，为EMD实现对序列的分解提供了良好的平台。

参考文献

[1]  熊学军，郭炳火，胡筱敏，刘建军．EMD 方法和Hilbert谱分析法的应用与探讨．黄渤海海洋，2002，26（2）．

[2] 余丽红．MATLAB课程教学改革浅探．广东白云学院学报，2009，16（4）．

[3] 朱艳科．MATLAB在大学数学教学和实验中的应用．广西科学院学报，2010年1（26）期（卷）．

[4] 付瑶，王红军，吴国新．EMD信号处理方法在LabVIEW和MATLAB中的实现．北京机械工业学院学报，2008，23（2）．

[5]  郭鹏．自回归滑动平均模型风速预测最大风能追踪策略研究．2010，37（2）.

[6] 杨刚，陈鸣．基于BP神经网络的风速预测和风能发电潜力分析．华东电力．2010，38（2）．

[7] 郭小燕，鲍海．风电场风速预测模型的研究．华北电力大学，2008.

[8] Ran Li, Yue Wang. Short-Term Wind Speed Forecasting for Wind Farm Based on Empirical Mode Decomposition. Proceedings of 11th International Conference on Electrical Machines and Systems, 2008.

[9] 栗然，王粤，肖进水．基于经验模态分解的风电场短期风速预测模型．中国电力，2009，9（42）．

[10] 王晓兰，李辉．基于经验模式分解的风电场风速趋势预测研究．兰州理工大学电气自动化，2010，2（32）．

[11] 胡晓，王志中，任小梅．一种改进的经验模型分解方法．信号处理，2006，22（4）．

[12] 刘慧婷等．基于多项式拟合算法的EMD端点问题的处理．计算机工程与应用，2004．