分形算法及C++实现
分形简介
我们人类生活的世界是一个极其复杂的世界,例如,喧闹的都市生活、变幻莫测的股市变化、复杂的生命现象、蜿蜒曲折的海岸线、坑坑洼洼的地面等等,都表现了客观世界特别丰富的现象。基于传统欧几里得几何学的各门自然科学总是把研究对象想象成一个个规则的形体,而我们生活的世界竟如此不规则和支离破碎,与欧几里得几何图形相比,拥有完全不同层次的复杂性。分形几何则提供了一种描述这种不规则复杂现象中的秩序和结构的新方法。
什么是分形几何?通俗一点说就是研究无限复杂但具有一定意义下的自相似图形和结构的几何学。什么是自相似呢?例如一棵苍天大树与它自身上的树枝及树枝上的枝杈,在形状上没什么大的区别,大树与树枝这种关系在几何形状上称之为自相似关系;我们再拿来一片树叶,仔细观察一下叶脉,它们也具备这种性质;动物也不例外,一头牛身体中的一个细胞中的基因记录着这头牛的全部生长信息;还有高山的表面,您无论怎样放大其局部,它都如此粗糙不平等等。这些例子在我们的身边到处可见。分形几何揭示了世界的本质,分形几何是真正描述大自然的几何学。
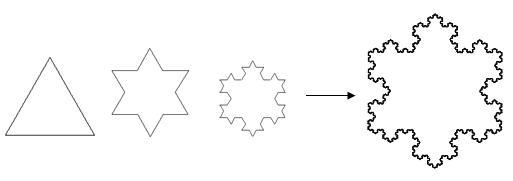
例如,首先画一个等边三角形,把边长为原来三角形边长的三分之一的小等边三角形选放在原来三角形的三条边上,由此得到一个六角星;再将这个六角星的每个角上的小等边三角形按上述同样方法变成一个小六角星……如此一直进行下去,就得到了雪花的形状。
2.分形中的迭代函数系统
相似变换是指在各个方向上变换的比率必须相同的一种比例变换;仿射变换是指在不同的方向上变换的比率可以不同的一种比例变换。
仿射变换的数学表达式为:
其中,a,b,c,d,e,f是仿射变换系数。
对于比较复杂的图形,可能需要多个不同的仿射变换来实现,而且,每个仿射变换被调用的概率不一定相同,所以引进一个参数概率p。a,b,c,d,e,f,p就构成了一个IFS码。
3.分形中计算机模拟算法
递归算法。
字符串替换算法。
迭代函数系统算法。
逃逸时间算法。
4.使用迭代函数系统算法对一棵树的C++实现程序
fractal.h文件:
#ifndef _FRACTAL_H
#define _FRACTAL_H
#include <cstdlib>
#include <ctime>
class CFractal
{
private:
float m[7][7];
float a;
float b;
float c;
float d;
float e;
float f;
float x;
float y;
float newx;
float newy;
int n;
public:
CFractal();
virtual ~CFractal();
void ifs(CDC* pDC);
};
#endif
fractal.cpp文件:
#include "stdafx.h"
#include "fractal.h"
CFractal::CFractal()
{
memset(m,0,49);
m[0][0]=-0.04; m[0][1]=0; m[0][2]=-0.19; m[0][3]=-0.47; m[0][4]=-0.12; m[0][5]=0.3;m[0][6]=0.25;
m[1][0]=0.65; m[1][1]=0; m[0][2]=0; m[1][3]=0.56; m[1][4]=0.06; m[1][5]=1.56;m[1][6]=0.25;
m[2][0]=0.41; m[2][1]=0.46; m[2][2]=-0.39; m[2][3]=0.61; m[2][4]=0.46; m[2][5]=0.4;m[2][6]=0.25;
m[3][0]=0.52; m[3][1]=-0.35; m[3][2]=0.25; m[3][3]=0.74; m[3][4]=-0.48; m[3][5]=0.38;m[3][6]=0.25;
x=0;
y=0;
a=0;
b=0;
c=0;
d=0;
e=0;
f=0;
newx=0;
newy=0;
n=300000;
}
CFractal::~CFractal()
{
}
void CFractal::ifs(CDC* pDC)
{
srand( (unsigned)time( NULL ) );
float r;
while (n>0)
{
r=(double)rand()/RAND_MAX;
char buffer[100];
if (r<=m[0][6])
{
a=m[0][0];
b=m[0][1];
c=m[0][2];
d=m[0][3];
e=m[0][4];
f=m[0][5];
}
else if (r<=(m[0][6]+m[1][6]))
{
a=m[1][0];
b=m[1][1];
c=m[1][2];
d=m[1][3];
e=m[1][4];
f=m[1][5];
}
else if (r<=(m[0][6]+m[1][6]+m[2][6]))
{
a=m[2][0];
b=m[2][1];
c=m[2][2];
d=m[2][3];
e=m[2][4];
f=m[2][5];
}
else
{
a=m[3][0];
b=m[3][1];
c=m[3][2];
d=m[3][3];
e=m[3][4];
f=m[3][5];
}
newx=(a*x) + (b*y) + e;
newy=(c*x) + (d*y) + f;
x=newx;
y=newy;
pDC->SetPixel( 300+100*x, 400-100*y, RGB(x*50*r,r*100,y*200*r));
--n;
}
}
可以在此程序上扩展,实现其他的一些分形图。
调用:
void CFractralView::Onfractral1()
{
// TODO: 在此添加命令处理程序代码
CDC *pDC=GetDC();
CFractal *f=new CFractal();
f->ifs(pDC);
ReleaseDC(pDC);
}
5.程序截图:



