1 实验目的

通过 matlab 简单的演示程序，理解 PCA 原理

2 实验原理

主成分分析 (principal component analysis PCA), 通过正交变换将一组可能存在相关性的变華转换成一组线性不相关的变華，转换之后的这组变華叫做主成分。常用千提取数据主要特征变華，常用千高维数据的降维。在用统计分析的方法研究多变華的时候，变華的个数太多，增加了复杂性，由千变華之间是有一定的相关性的，也就是说不同的变華所代表的全局信息是有重叠，有冗余的。其算法流程如图 1所示：

图 1: PCA 算法流程图

3 实验内容

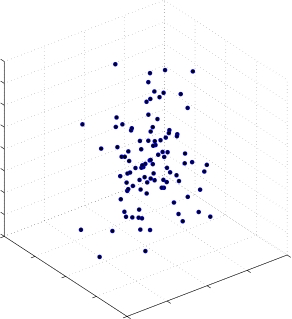
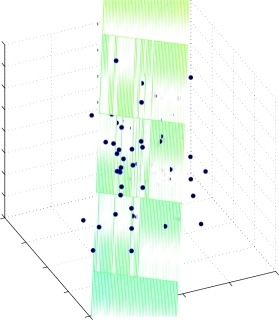
如图 2所示绘制随机的 3 维点，如图 3所示，选取特征值最大的两个特征向華进行投影，绘制其投影平面，如图 4所示，绘制出 3 维到 2 维的投影垂线以示意这个过程的原理。如图 5所示为最后投影得到的二维点在三维坐标中的位置，可以看到，这些点都位千一个平面上，如图 6所示为二维点到一维点的投影线，所选的投影基为特征值最大的特征向華，如图 7所示，绘制了二维到一维的投影垂线，如图 8所示为二维降为一维的点。整个过程演示了一个三维特逐渐降为一维的过程，特征有所损失，但是仍能被区分。

2

1.5

1

0.5

0

−0.5

−1

−1.5

−2

2

1 2

0 1

0

−1 −1

−2     −2

图 2: 随机三维点

x 2.67049435798803e1−y 5.058306494383652e−1

2

1.5

1

0.5

0

−0.5

−1

−1.5

−2

2

1

0

2

−1 1

0

−1

y −2 −2

x

图 3: 三维到二维投影面

2

1.5

1

0.5

0

−0.5

−1

−1.5

−2

2

1

0

−1

−2 −2 −1.5 −1 −0.5 0 0.5

y

x

1 1.5 2

图 4: 三维到二维的投影过程

x 2.67049435798803e1−y 5.058306494383652e−1

2

1.5

1

0.5

0

−0.5

−1

−1.5

−2

2

1

0

−1 2

1

y 0

−2    −2

x

图 5: 三维到二维的投影点

2

1.5

1

0.5

0

−0.5

−1

−1.5

−2

2 2

1 1

0 0

−1

−2 −2

y x

图 6: 二维到一维的投影线

x 2.67049435798803e1−y 5.058306494383652e−1

2

1.5

1

0.5

0

−0.5

−1

−1.5

−2

2 2

1 1

0 0

−1

−2 −2

y x

图 7: 二维到一维的投影过程

2

1.5

1

0.5

0

−0.5

−1

−1.5

−2

2 2

1 1

0 0

−1

−2 −2

y x

图 8: 二维到一维的投影点

4 心得体会

1. 使用 PCA 对数据进行降维的思路：将输入的样本看成一个随机向華，即

X⃗  = {X1, X2, X3, ...XN } N  = 0, 1, 2... (1)

有 M 个样本，说明发生了 M  次 X⃗

事件，X⃗

有 N 维，每一维为单独的随机变華 XN ，若要将降维，

降维后的需满足其内部各维之间的协方差为 0，已保证降维后的数据无冗余，每一位表示的信息不正交不重叠；同时各维的方差需要最大，因为方差大代表着数据集中性越差，说明越方便被卅别。随机向華协方   差矩阵中，各维均值位千对角线，协方差位千其他非对角线位置，我们需要对角线值最大，其他位置值为  0，这不免让我们想到了矩阵的对角化。对角化完成的功能真是将矩阵除对角线为其他元素变成 0. 矩阵的对角化表达式为

B  = T −1AT (2)

其中 A 为待对角化矩阵，T 为 A 的特征向華组成的矩阵，这里我们将 A 看成是的协方差矩阵，那么 T 就是这个协方差矩阵特征向華组成的矩阵。对角化的过程已经完成了协方差 0 的任务，接下来使各维的方差最大，即 B 的对角线元素最大。因为特征值大的特征向華是矩阵变换的主要方向，所以其占的变换成分应该比较大，对 B 的对角线元素影响也比较大，所以这里才有根据特征值来排序特征向華来组成矩阵 T 的方法。按照成分的贡献率，可以执行降维，维度贡献率不能少千 80%。

在使用式 3计算协方差矩阵的时候，A 为样本数据集矩阵，N 为样本维数，需要注意的是样本数据集

A 必须去均值，即使样本各维均值为 0，这样使用该公式计算出来的才是协方差矩阵。

C  = 1 AAT (3)

N

在执行数据降维的时候，从二维数据降至一维的变换为 A，得到的这个一维的数据是以 A 的基为基的坐标再乘以这个基的范数，若这个变换本身就同其基一致的话，得到的一维数据为其投影长度。Matlab 中计算特征向華的函数已经完成了特征向華单位化的操作，所以，将数据同其内积得到的便是投影长度。   实验中涉及将这个投影长度在原来的维度中显示的问题，只要将这个投影长度乘以原来投影的基向華就 行了。

Matlab 中如果要在上写文中索引当前 axes，进行绘图，只需要进行一次 hold on, 就可以防止 plot 旬柄的自动回收。

5 代码

PCAdemo.m

1 f u n c t i o n PCAdemo

2 c l o s e a l l ; c l e a r ; c l c ;

3 h_figure=f i g u r e ;

4 mu=[0 0 0 ] ;

5 %协方差矩阵 ， 对角为方差值 0 . 3 ， 0 . 3 5

6 dim=3;

7 var =[ 0.2 0 0 ; 0 0 . 5 0 ; 0 0 0 . 8 ] ;

8 samNum=100;

9 data=mvnrnd(mu, var ,samNum ) ;

10 h_plotMain=p l o t3 ( gca , data ( : , 1 ) , data ( : , 2 ) , data ( : , 3 ) , ’ o ’ , . . .

11 ’ MarkerSize ’ , 5 , ’ MarkerFaceColor ’ , ’ k ’ ) ;

12 xlim ([ −2 2 ] ) ; ylim ([ −2 2 ] ) ; z l im ([ −2 2 ] ) ;

13 g r i d on ; a x i s square ; hold on ;

14 pause ( ) ;

15 covdata = cov ( data ) ;%求协方差矩阵

16 [ e i g Ve cto r , e i g Val u e ]= e i g ( covdata ) ;%求 协 方 差 矩 阵 的 特 征 值 和 特 征 向 華

17 e i g Val u e=d iag ( e i g Val u e ) ’ ;

18 [ eigValue_sort , IX]= s o r t ( eigValue , 2 , ’ descend ’ ) ;

19 e i g Ve c to r _s o r t = [ ] ;

20 f o r i =1:dim

21 tempIX=IX( i ) ;

22 e i g Ve c to r _s o r t =[ e i g Ve c to r _s o r t e i g V e c to r ( : , tempIX ) ] ;

23 end

24 base_3to2=e i g Ve c to r _s o r t ( : , 1 : 2 ) ;%三维降 2 维

25 base_3to1=e i g Ve c to r _s o r t ( : , 1 ) ;%三维降 1 维

26   base_3to2=base_3to2 ’ ;

27   base_3to1=base_3to1 ’ ;

28 %%%%%绘制3 维变成 2 维度的投影平面%%%%%

29 A=base_3to2 ( 1 , : ) ;%新基 i 帽 ( 相对原基 )

30  B=base_3to2 ( 2 , : ) ;%新基 j 帽 ( 相对原基 )

31 C=[0 0 0 ] ;

32 syms x y z ;

33 D=[ ones ( 4 , 1 ) , [ [ x , y , z ] ; A;B;C ] ] ;%由 空 间 解 析 几 何 的 内 容 知 道D的 行 列 式 等 千 零 就 是 平 面 方 程 。

34 detd=det (D) ;

35 z=s o l v e ( detd , z ) ;

36 ezmesh ( z ,[ −2 , 2 , −2, 2 ] ) ;

37 pause ( ) ;

38  %%%%%%%%%%%%

39  data_proj3_2=base_3to2*data ’ ;%投影到新基坐标 ( 相对新基 )

40  data_proj3_1=base_3to1*data ’ ;%投影到新基坐标 ( 相对新基 )

41

42 data_proj3_2=data_proj3_2 ’ ;