行星齿轮变速箱的分析方法
摘要:本文提出了一种分析行星齿轮变速箱在外部因素作用下速度、扭矩和功率的评估方法,以及齿轮箱的总传动比的分析。该方法是基于描述每个行星齿轮机构方程和对于不同外部因素分配适当的代码的规则来分析的。该方法主要关注行星齿轮传动里功率流是怎么样传递的,以及功率损耗。以下分析一个行星齿轮箱,以说明所提出的方法的运用。
关键词:行星齿轮,行星齿轮箱
1.导言
《机械原理》(Principles of Mechanisms) (Willis, 1841)被广泛认为是是首个出版现在所谓的运动的专门领域的书籍,在其发表的文学作品里第一时间讨论分析周转轮系的模型。后来,Willis在Analysis and Design of Mechanisms 里详细的提出了的其发现的周转轮系每个部分的转速的计算方法,以及三和四的齿轮传动设计具体的方法。随后,Tsai (2001)进一步的发展了该方法,通过使用图论,并延伸“包括负杠杆比率的行星齿轮组的一个杠杆表示的传统的概念”。这些方法已经发现适合一系列的应用。由于它们的优点如:设计紧凑,自动转移,并增加了控制的可能性,行星齿轮箱已频繁被用来替代其他的传动方法。
分析了一种行星齿轮箱的目的是评估的齿轮传动比,功率流和每个阶段效率。本文提出了一种利用功率流元素分析行星齿轮变速箱理论的方法。这种方法是建立在能使用
高效的计算功能的计算机基础上,并评估齿轮传动比的符号表达式,扭矩和功率流等所有元素。本文提出的方法是应用在一个固定的不变的速度的工作制度条件下。(dω/dt=0);因此,齿轮和轴的惯性被忽略。
2.功率流理论的应用
行星齿轮箱是由一个或更多的行星齿轮机构(EGM)、离合器和飞轮组成。每一个元素可以用线性方程来描述,可以计算速度,力矩和功率(Fogarasy and Smith,1995; Du and Zhang, 2007)。
功率流图是一个系统线性方程组一种图形表示形式。功率流图建立了输入变量(速度,转矩和功率)和输出变量之间的联系,强调功率流是如何传递的(Ryu et al., 2009)。因此,功率流图表示了一个可视化工具,以及一个分析工具,很容易的就可以生成一个行星齿轮箱图。
通过一个元素功率的传递可以通过下面的公式计算:
P=M⋅ω (1)
其中P是功率(W);M是扭矩(Nm);ω是角速度(弧度/秒)。
上述公式表明,功率受到以下两个因素的作用而产生的:负载因子(转矩)和运动因子(速度)。转矩和速度是可正可负的;因此,功率是可正(输入或收敛的功率)可负(输出或紧急功率)。
功率流图使用以下的基本要素作出的:
l 节点,其至少传递一个因素(负荷或运动);
l 不改变的因素的传递功率流弧。
图形元素遵循以下两个原则:
(1)每一个节点,收敛功率的总和等于紧急功率和耗散功率总和;因此功率的总和是零:
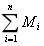 .
.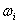 +P
+P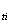 =0 (2)
=0 (2)
其中P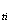 我代表节点i的耗散功率
我代表节点i的耗散功率
这条规则是来自于行星齿轮箱结构节能的一般规律
(2)对于每一个结点,其力矩之和为零(扭矩平衡定律):
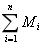 =0 (3)
=0 (3)
有好几种种用来描述行星齿轮变速箱运动学结构的节点类型。最常用的节点被总结在表1。使用下表中所列的图形符号可以将任何运动的变速箱可以转化为功率流图。
3。行星齿轮机构的基本原理
行星变速箱由一个或多个行星齿轮机构的离合器和制动器组成。其机构运动简图如图1所示。
因此,行星齿轮由3个固定轴元素(太阳轮,齿圈和载体臂)和一个旋转轴元素(行星齿轮)组成的。图1给出了行星齿轮机构。行星齿轮一般具有2个自由度(DOF),但也有更多的自由度的行星齿轮机构,例如,the Ravigneux mechanism.。
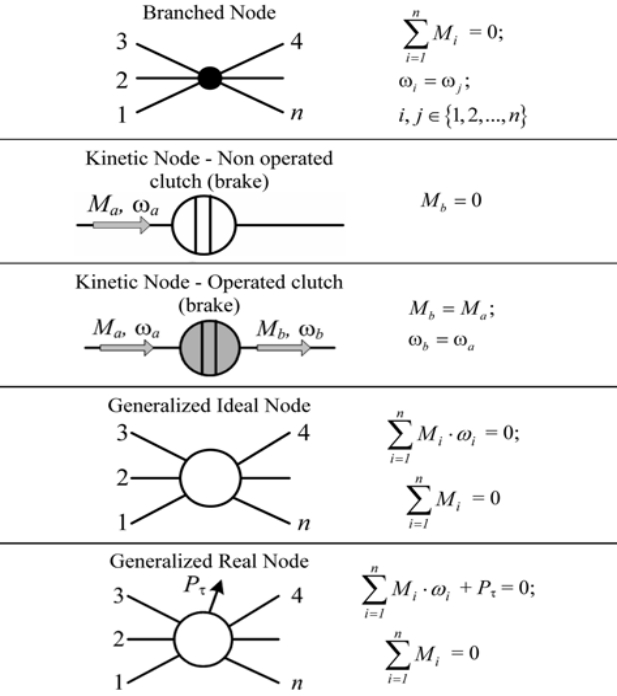
表1 主要类型的节点。
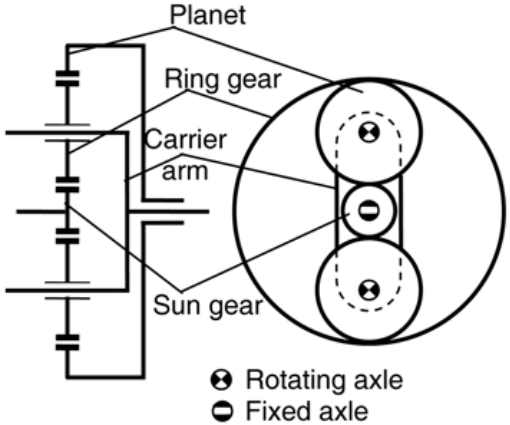
图2 行星齿轮
根据Willis原理,导出描述EGM的运动学方程如下:
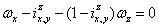 (4)
(4)
当功率从元素x传送到元素y并且z轴是固定是,这里的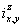 是传动比。
是传动比。
该指数表明EGM要素有以下规则(其中n表示在变速箱里EGM总数):
l 对于太阳齿轮:1, 4, …, 3j – 2, …, 3n – 2;
l 对于环形齿轮: 2, 5, …, 3j – 1, …, 3n – 1;
l 对于行星架:0, 3, …, 3j – 3, …, 3n – 3.
总的来说,应用上述列出的指标的,方程(4)成为下式:
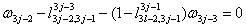 (5)
(5)
对于一个单一的EGM(在这种情况下,J = 1),方程具有以下形式:
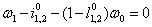 (6)
(6)
如果行星架固定(ω0 = 0),EGM转变为一个具有固定轴普通齿轮机制;因此,方程定义的比率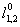 :
:
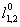 =
=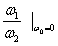 (7)
(7)
这个普通的机制,EGM常数定义为:
K=从动齿轮的齿数的乘积/主动齿轮的齿数的乘积
或者对于EGM表示常数:
K=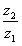 (8)
(8)
在一般情况下,根据EGM结构:
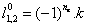 (9)
(9)
或者:
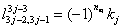 (10)
(10)
总之,2个自由度的EGM运动学是完全由有3个变量的一个单一的方程描述的。
EGM各要素之间的扭矩分配由以下方程组给出了:
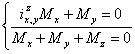 (11)
(11)
从第一个方程,得到下面的关系结果:
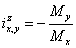 (12)
(12)
一个理想的EGM(无损耗),方程(12)是类似于方程(7),但有不同的含义。方程(7)定义的是运动比,方程(12)定义的是扭矩转化率。一个理想的EGM,两者的比值(各自的运动和转矩变换)分别是相等的数值。
对于EGM的每个外部元件,功率利用下面的公式计算:
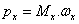 (13)
(13)
2个自由度的EGM,如图1中所示。它被认为是一种理想的齿轮啮合,所以没有功率损耗。在实际情况中,由于摩擦齿轮的啮合产生功率损耗,失去的功率转化为热耗散。
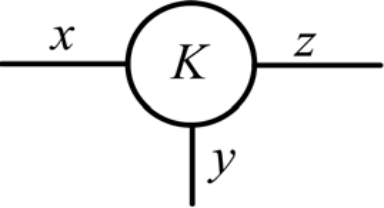
图2 2个自由度的EGM功率流图
对于功率损耗的存在要修改力矩,但对EGM的外部元件的速度没有影响。因此,方程(7)仍然是有效的,但真正的扭矩转化率由下式给出:
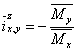 (14)
(14)
这里符号“~”(波浪线)表示实际的扭矩和功率,以表明他们不同于他们各自的理想值。
只考虑两个外部元素节点,传输效率的效率是由下式给出:
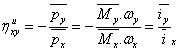 ; u=
; u=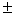 1 (15)
1 (15)
这里指数值需要根据的功率流的意义选择。包括行星齿轮在内的用于传输的指数,你可以使用下面的关系式计算出其值:
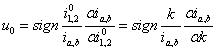 (16)
(16)
这里指数A和B分别代表输入轴和输出轴。
4.行星变速器分析
根据传动结构,在一个行星齿轮箱里,功率流从输入a到输出b有一个或多个路径。
分析行星齿轮变速箱需要计算每个阶段的变速箱总比、EGMS中功率流的分布以及每个阶段的整体效率。为了解决代数问题可以通过使用常用软件,用所提出的方法可以有效的计算这些数据。
使用的变速箱作为例子可以最好的说明这种方法;运动图如图3所示
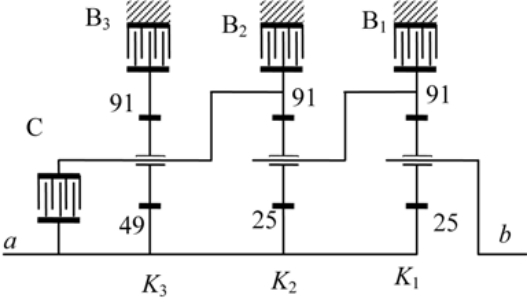
图3 变速箱的运动图
所考虑的变速箱由3个包含常数K1……K3的行星齿轮与3个用B1和B3……表示的制动器以及一个离合器组成。此外,它可以实现4个前进速度。输入轴是用a表示,输出轴用b表示。该变速箱是ZF 4 HP 250传动部分;相反的转速是使用一个EGM作为逆变器来实现的。刹车和离合器的使用顺序表2给出了。
行星齿轮箱的等效功率流图 如图4所示。
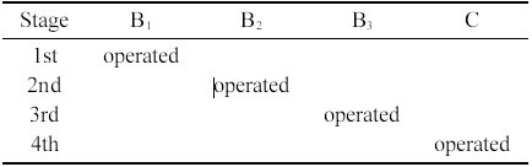
表2刹车和离合器序列
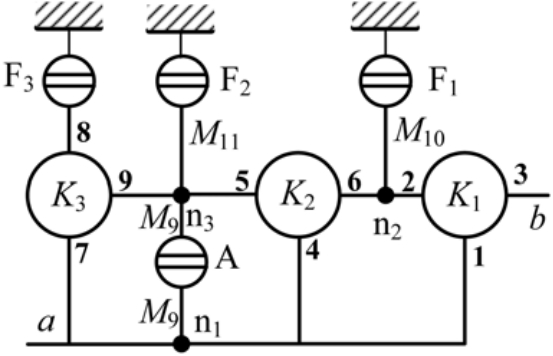
图4 行星变速箱的功率流图
行星变速箱分别由3个含有常数K 1,K 2,K3的行星齿轮机构,3个制动器F1,F2,F3和一个离合器A组成。功率流图包括分支节点N1,N3…。输入轴和输出轴分别标记为a和b.
从功率流图可以快速的看出EGM外部元素之间的联系,方便的变速箱比的计算。
分析行星齿轮箱的第一步是计算变速箱传动比。
对于每个EGM,都有一个单一的运动方程可以得到,通过重新排列的顺序,得到下面的方程:
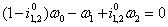 (17)
(17)
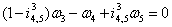 (18)
(18)
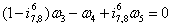 (19)
(19)
外部EGM要素之间的联系是由以下方程描述:
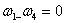 (20)
(20)
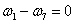 (21)
(21)
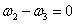 (22)
(22)
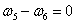 (23)
(23)
输入元素a假定有一个已知的速度:为方便起见,假设
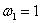 (24)
(24)
因此,齿轮箱的比例将会是:
 (25)
(25)
方程(17)~(24)对于变速箱各阶段都是有效的。根据移动图表2当一个单一的制动器或离合器运动时就是一个特定的阶段。因此,对于四个阶段下面的公式可为:
l 第一个阶段:
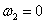 (26)
(26)
l 第二个阶段:
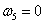 (27)
(27)
l 第三个阶段:
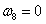 (28)
(28)
l 第四个阶段:
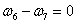 (29)
(29)
从关系式(26)~(20)添加一个等式(17)~(24)这组方程,得到9个方程的联立方程组。因此,这九个变量ω0……ω8可以计算出来。
计算可以象征性的进行;因此,变速箱的传动比可以用一个有理函数表示,有理函数的变量是EGM的常数函数。求解每个阶段的联立方程组,得到以下的速度。

表3 对于EGM的外部元件的速度。
为了计算力矩,每个节点可以推导出下面的方程:
l 对于EGM 1 :
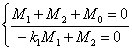 (30)
(30)
l 对于EGM 2 :
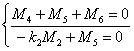 (31)
(31)
l 对于EGM 3 :
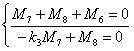 (32)
(32)
l 对于分支节点1:
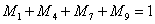 (33)
(33)
l 对于分支节点2:
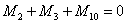 (34)
(34)
l 对于分支节点3:
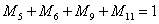 (35)
(35)
以下限制分别适用于每个阶段:
l 对于第1个阶段: ;
;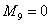 ;
;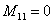 (36)
(36)
l 对于第2个阶段: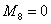 ;
; 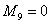 ;
;  (37)
(37)
l 对于第3个阶段: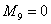 ;
;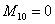 ;
;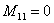 (38)
(38)
l 对于第4个阶段: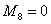 ;
;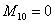 ;
; 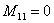 (39)
(39)
方程(30)~(35)和(36)~(39)的其中一个限制条件组成的联立方程组;例如,对于第一个阶段,联立方程组如下:
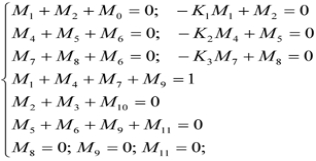 (40)
(40)
考虑到方程(9),(15),和(16)和功率损失的真实情况,系统的联立方程(40)成为:
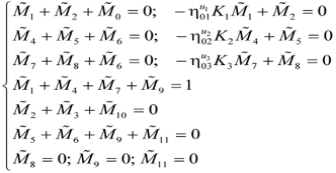 (41)
(41)
指数U1,U2和U3,可以用变速箱的传动比通过表3决定。
计算了变速器的效率时,方程(15)适用于EGM的总体结构:
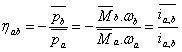 (42)
(42)
用变量是EGM常数的一个有理函数表示变速箱比:
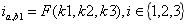 (43)
(43)
在功率损耗存在时,扭矩转化率是具有相同的有理函数,但具有不同的变量。
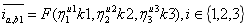 (44)
(44)
进行数值计算时,EGM的效率平均值为:η= 0.9653。最后的数值结果列于表4。
在第一阶段,功率降低的流程图如图5所示。可以看到的行星齿轮机构K1有助于的功率流传递。通过分析导出的第一阶段的功能结构方程可以得到同样的结论。
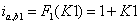
因为常数K1是唯一的变量,所以这个EGM只传递功率流。
第二阶段,传动比的计算:
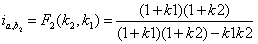
并且功率流的传输是由两个EGM实现;从图6中所示的图得到相同的结论。
这个阶段,功率流是通过两种途径传播,可以看到的功率流在每链中的传送是同一方向的。换句话说,在闭环系统里没有内部功率流。
在第三阶段,制动器F3是工作的。这个阶段的功率流图如图7所示。可以看到,在第三阶段中,所有的行星齿轮机构有助于功率流传递。输入功率将在三个EGM中分开,标记为K2和K1的EGM作为总的机制。
5.结论
分析行星齿轮箱所提出该方法的主要优点:
(1)它可以用来计算所有路径的齿轮传动比、速度、扭矩和功率。
(2)用计算机计算,并且所提出的算法可以使用常用软件求解。(3)如果传动比的数值是已知的它可以评估EGM常数。
此外,所提出的方法可以开发成适用的应用软件,造福汽车专业本科学生和汽车变速箱的专家。

表4 速度、扭矩和功率流的计算结果
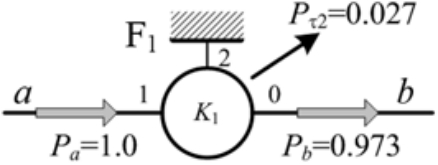
图5 功率流图的第一阶段
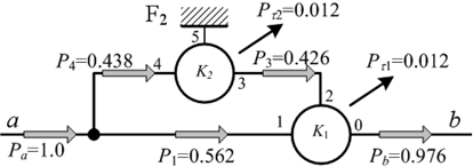
图6 功率流图的第二阶段
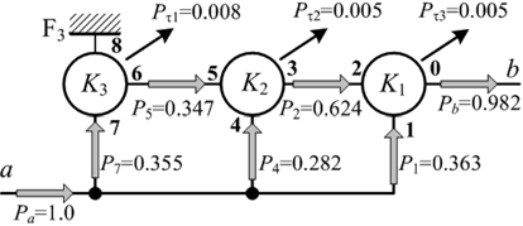
图7 第三阶段的功率流图



