车灯线光源的优化设计方案

[编者按]本文的主要特点是：在建立反射光强度的数学模型时，用反射点投影至测试屏目标点的变换的Jacobi行列式来刻画反射面元面积与该面元的反射光在测试屏照射到的微元面积之间的精确关系，并给出了相应的近似模型。

遗憾的是在实际离散化计算时，作者们做了过度的简化，未能真正应用上述模型，计算结果偏小。

[摘要]本问题是一个车灯线光源的优化设计问题。

首先，我们建立了一个连续的数学模型来描述这个优化问题，此模型研究了线光源上任意一点发出的光线经过抛物面反射后到达光屏的情况， 对于给定的考察点(B或C)得到一个联系该点与光的发射点，反射点这3个点关系的方程组。由于光在传播过程中会有发散的现象，我们用Jacobi行列式做了一个变换来描述这种散射。根据C点的光强度必须大于一个确定的值(文中设为1)，B点的光强度必须大于该值的2倍的约束条件将这个问题抽象成一个非线性规划问题。

由于解非线性规划问题是很复杂的过程，我们选择了将连续模型简化成一个离散模型。但是离散模型将光离散成一条一条光线时，一般不能考虑光在传播过程中的散射问题。根据我们连续模型中用Jacobi行列式算出的结果知可以考虑光在传播过程中的散射问题，但是Jacobi行列式是很难求出来的，为了解决这个困难我们将光的散射用连续的方法做了一个简化。简化的方法是用向量投影的方法粗略作出了两个面积微元之间的关系，从而得到了光线打在光屏上的散射效果与光线的起始单位方向向量和该光线经抛物面反射时的反射点的坐标的关系。

运用以上的离散模型的算法，得到最优的线光源长度为3.39mm。

[关键词]线光源,非线性规划,散射,Jacobi行列式,向量投影.

1.问题的重述(略)

2.基本假设:1.不考虑光在空气中传播时的损耗.

2.点光源发光时,在各个方向上产生的光强度是一样的.3.参数说明: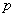      旋转抛物面的焦参数 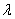     线光源光能线密度,可以表示单位长度光源产生的光强度量2 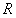     线光源的长度 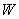     线光源半轴长发光的总强度量

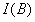    B点接收到的光强度(光强度量的面密度) 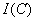   C点接收到的光强度(光强度量的面密度) 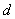      旋转抛物面的深度 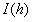    光在空间传播时在距离光源h处的光强度Q        某点光源的发光强度量n        每个发光点向空间发射的光线数 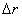     每个离散点光源的长度Δm      每束光线可以产生的光强度量 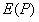 抛物面上可以将光线反射到P点的所有点的集合      光屏上每个小网格的面积

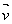        测试屏的单位法向量(沿z轴负方向)4.问题的分析:    本问题是一个面镜反射的几何光学问题.目的是要求在满足题目要求(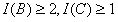)时对线光源的长度(2R)和单位发光密度(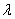)进行优化,使得线光源的发光总强度量最小.

对于其中的考察点,例如B,首先要考虑光源上哪些点可以经过抛物面哪些反射点反射到考察点B.然后根据他们之间的位置关系算出从线光源上某点射出的光线在到达考察点B时,考察点B所接收到的光的强度.再对该考察点上所接收到的所有光的强度进行积分,算出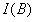,将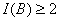,作为问题的一个约束条件,同理算出关于C点的一个约束条件.问题就变成了一个带约束条件的优化问题.

5.模型的构建

5.1反射点和发光点以及受光点之间的关系

考虑线光源上一点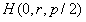发射一条光线经过抛物面上一点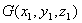射到光屏上某点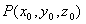的情况.

如图.1,抛物面方程为

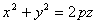
G点的单位内法向量为

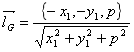
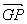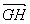将向量和单位化得

图.1

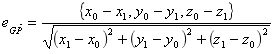
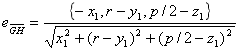
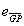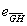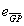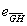若光线可以从H出发经过抛物面上的G到达光屏上的P,则向量和的和与G点的单位内法向量同向,即向量和的和与G点的单位内法向量的向量积为0,即

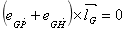
令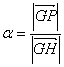,可以将原方程组化简为

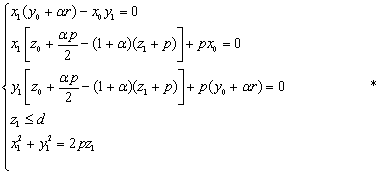
由于方程组*中前三个方程只有两个是独立的,则在前两个方程中可以任意去掉一个,方程组就决定H、P和G三点之间的位置关系.

5.2光线经光屏反射过程的数学描述

在线光源上取一点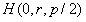,过该点沿单位向量

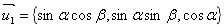
做一条直线交抛物面于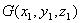,则

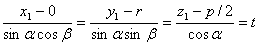
又G在抛物面上,则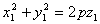         

则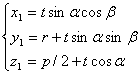        

G点的单位内法向量为

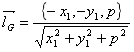
则表示反射光线方向的单位向量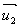如图.2,可知

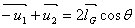
又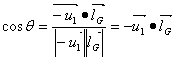          

则经抛物面反射的单位向量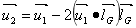      

5.3光在传播过程中的发散

光在空间传播时是在整个空间上均匀发散的. 我们用光强度量来表示光源在整个空间发射出去的光能,用光强度量的面密度来度量光发散到某个点在该点产生的光强度.当发光强度量为Q的点光源发出的光传播到空间某点时，由于光波是球面波,则可知

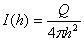
那么当长度为dr的线光源（当成点光源看）从H发出的光传播到G时,G点所接收到的光强度为

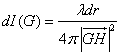
现在讨论光从G反射到P点时光强度的变化情况. 在G周围取一个小的面积微元

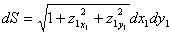
从方程组*中可以确定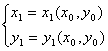              

则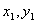对于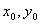的Jacobi行列式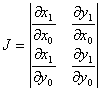       

则可得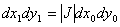                      

而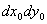为光屏上的面积微元,记为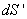,即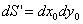     

则可以推出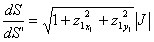                     

G点接收到的光强度量

又由于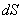上的所有光线全反射到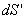,即它们两个面积微元上的光强度通量相等

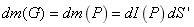
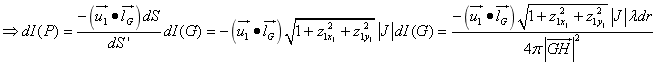则P点的光强度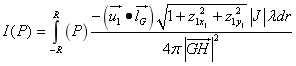      

5.4非线性规划问题

通过以上的分析可以知道B点的光强度为

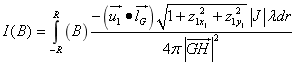
同理,C点的光强度为

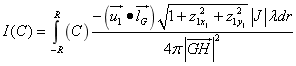
根据题意,本问题的约束条件为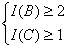            

我们的目标是使线光源半轴发光的总强度量最小,即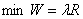       

那么本问题可以归结为一个求非线性规划最优解的问题

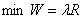
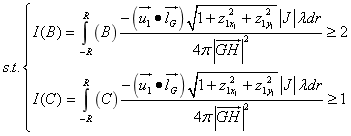
6.模型的简化与求解

6.1光源发光的离散化

以上的模型最终是要求解一个非线性规划问题,解这类问题通常需要很大的计算量,而且很容易陷入局部极小值.现在我们将模型中连续的线光源离散成许多点光源,而且将光的均匀发散离散化,考虑点光源的光以n条光线的形式对外发散. 将光屏也分割成许多小网格,将经过抛物面反射到屏上各个网格内的光所具有的光强度量进行求和再除以该网格的面积,定义为该网格内的光强.

若每个离散点光源的长度为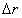,则该离散点发出的一条光线可以产生的光强度量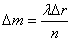                          

6.2光传播过程中发散的一个近似处理

对于光在传播过程中的散射对射到光屏上后强度的影响模型中是用Jacobi行列式体现的.但是这个Jacobi行列式的表达式是很复杂的,我们给出一种近似处理这种散射影响的方法.这个近似的简化是在连续条件下考察面积微元得到的,但是这个结果对于离散的模型同样适用.

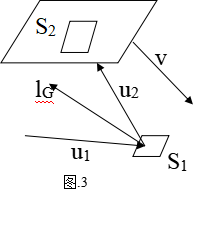如图.3,一束光线射到曲面上的一个单位法向量为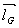的面积微元S1后反射到一个单位法向量为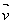的平面上形成一个面积微元S2.由于面积微元很小,我们近似的认为反射光线沿一个方向射出.

我们进行反向思考,由于S2是S1沿单位向量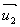投影后在单位法向量为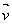的平面上的投影,那么S2和S1在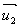方向上的投影面积应该是相等的,即

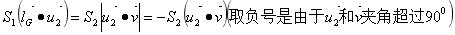
S1面上接收到的光强度量

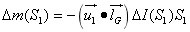
又由于S2和S1上通过的光强度通量相等,即

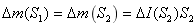
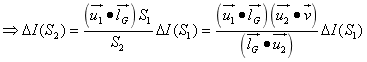
光线从线光源上的H到达抛物面上的G点时的光强度根据[5.3光在传播过程中的发散]可以得到,光从G传播至P时运用以上方法可以得到

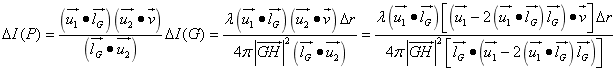
这时每条光线从H射到P时在P所在网格产生的光强度量

那么P点的光强度为

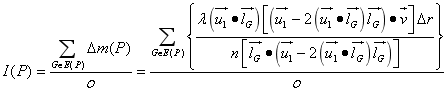
6.3问题的求解

根据以上对模型的离散简化得到一个离散优化模型

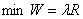
s.t.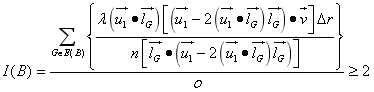 

为了方便用计算机求解，我们对上面的优化模型进行转化，得到

min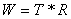    

s.t.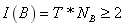     

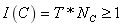
其中，T为每条光线带的光强，

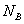为打到以B为圆心，以2cm为半径的圆内的光线条数，

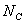为打到以C为圆心，以2cm为半径的圆内的光线条数。

对于这个问题的求解我们采取分步等步长搜索的方法.具体步骤如下:

步骤一

将线光源细化成许多个小的光源,每个小光源的长度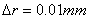.将整个空间的立体角4π分成n=40000份.在B和C点周围分别做一个半径为2cm的圆.

步骤二

将每个小光源发射出的光离散为以40000条光线的形式发射出去,每条可以射到抛物面上的光线经抛物面反射后会在光屏上打下唯一的一个点.如果该点在以B(或C)为中心的圆内,就将打在这个区域的光线条数加1.

步骤三

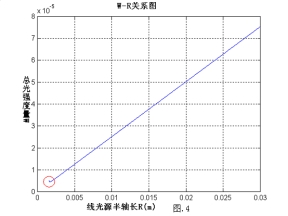
首先在R∈(0,30mm)内以为0.1mm步长对R进行搜索,得到的W-R的图象如下图.4,对图中划在圆圈内部的W-R曲线进行放大,如图.5.

我们从图中可以看出最优的R出现在1.5mm到3mm区域内.现将进一步搜索的区域定为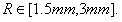

步骤四

在区间R∈[1.5mm,3mm]内以0.005mm为步长进行搜索,得到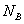和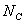关于线光源半轴长R图形(如图.6).

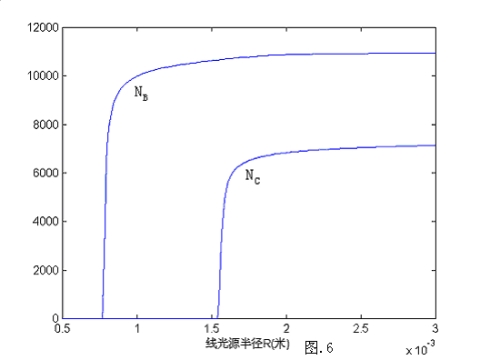
利用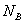、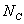的值,对优化模型进行求解,得到在R∈[1.5mm,3mm]区间内W-R图线,如图.7

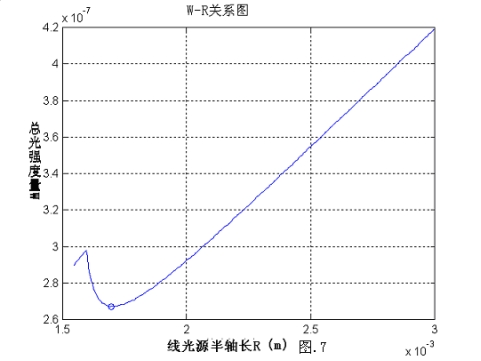
在图中圆圈（即最优化解）附近点的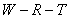数据列表如下

从优化的结果数据，我们得出最优的线光源的半轴长为R=1.695mm.此时这个线光源的长度2R=3.39mm.

7.问题第二问的解答(略)

8.设计规范的合理性验证

8.1合理性的分析

本题中涉及到的灯是车的前照灯.前照灯是汽车在夜间行车或在能见度较低的条件下,为驾驶员提供车道照明的重要设备,所以前照灯必须有足够的发光强度和正确照明区域.不合格的前照灯会使驾驶员对前方道路情况辨认不清,或者在与来车交会时造成对方驾驶员目眩等,从而导致事故的发生.

一个合理设计规范应该是在这个规范下做出的最合适的车灯具有以下照明效果:

1. 车灯正前方为了照亮车道,应该亮度很大.

2. 前照灯也要照亮邻道,使驾驶员能清楚把握邻道的情况,故车两侧附近也应该有较高的亮度.

3. 而更远一点的距离,如果太亮的话,就有可能使迎面而来车辆的驾驶员目炫,而使发生事故的机率加大,故亮度要较低.

8.2设计规范的随机模拟验证

根据以上的合理性分析,我们需要用实验的方法检验这个规范的合理性.我们在以上做的模型中要求点光源在空间各个方向上产生的光强度是一样的,但是考虑到光在实际传播过程中,由于种种因素的影响,会使光源在发光时在各个方向上发光的强度是不一样的.我们用计算机对线光源经过抛物面反射发光进行随机模拟实验.具体步骤如下:

步骤一

用Matlab随机数函数UNIFRND( )产生点光源向空间发射光线的随机单位方向向量.

步骤二

用这些随机单位方向向量对我们上文已经求出的最佳光源发光进行模拟,在离散成许多小区域组成的光屏上统计每个区域内的光强度.在光屏上作出如下光强度分布图.（图.9）

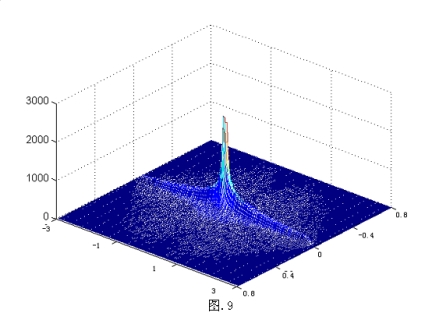
上图中,光屏上某点的光强度用高度来体现，高度越大，亮度越大.从上图可以很明显的看出来灯的正前方光的强度很大,而且两侧光的强度和正前方相比很小,但是和其他区域相比还是比较强的,这就从实验的角度验证了这个设计规范的合理性.以下作出该图象的俯视图.(图.10)

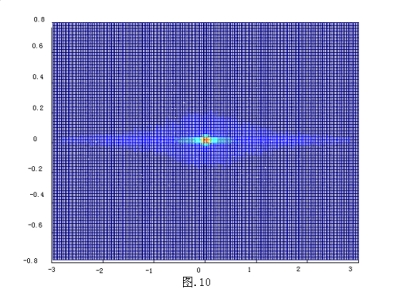
从这个图中就可以更直接的看出光屏上各区域光强度的分布.中间部分的很亮可以为夜间行车提供良好照明,一个车宽附近的区域也较亮,可以清楚看到邻道的情况,更远一点的距离亮度迅速减弱,这样与来车交会时不易造成对方驾驶员目眩,从而有效地避免事故的发生.

9.模型优缺点分析

对于本题可以建立连续和离散两种模型.前者可以将本题抽象成一个非线性规划问题,但是求解的过程比较复杂,很容易陷入局部极小值的情况,而且对于问题第二问的求解没什么帮助,但是优点是如果初值取的好可以很精确的求出本题的结果.后者的优点是对于算法而言不是很复杂,求解结果很快, 同时可以很方便的解决问题第二问,但是求解得到的结果不是很精确,而且只能给出数值解,并且将光离散成光线以后就不能体现光在传播过程中的散射.综合以上考虑,我们提出的这个模型既拥有离散模型的优点,又运用一个连续模型的变换结果,考虑了光在传播过程中的散射,比较精确地刻画了光在传播过程中的散射.

参考文献：

1．《解析几何》，方得植 编，高等教育出版社,1986.

2．《应用光学》（修订本），天津大学 张以谟 主编，机械工业出版社,1988.

3．《工程光学》，张凤林 孙学珠 主编，天津大学出版社,1988.

4．《科学计算技术与Matlab》,刘则毅 主编，科学出版社,2001.

5．《解析几何》，章学诚 编，北京大学出版社,1989.

6．中国汽车检测维修网：http://www.auto-tester.com

An Optimal Design of Linear light source

Abstract:Firstly, we developed a continual mathematic model to characterize this problem. It demonstrated how the beam reaches the screen by the reflection of the paraboloid. It was a nonlinear programming problem. Because it was very difficult to solve such a problem. Then we simplified it into a discrete model.  Based on this model, we wrote a Matlab program and got the optimal length of the linear light source was 3.39mm. Finally, we use random simulation to verify the design scheme.

Key word: linear light source, Jacobi determinant, nonlinear programming, projection of vector,