摘 要
随着战场电磁环境的日趋复杂,战场中截获到的雷达信号也日益繁杂,不仅调制种类繁多,而且叠加进入接收机的分量个数也在加剧。在复杂的截获信号中得到各分量的类型和参数,进而对各辐射源进行正确识别和高效干扰是制定战略决策的重要因素。要正确的分析截获的多分量雷达信号,将其包含的分量提取和重建是一个不可避免的过程,本文重点基于信号的时频分布特征对多分量信号的提取和重建技术进行探讨。
首先,总结了常见雷达信号类型的时频特征和稀疏特征,并进一步研究了多分量雷达信号在时频分布中存在的规律。研究发现计算时频分布时不可避免的需要在干扰项抑制和信号项模糊之间均衡选择,因此引入自适应方向核的二次时频分布。该时频分布根据信号项和干扰项在模糊域的特征,通过自适应选择模糊域方向核,在干扰项抑制和信号项模糊之间达到较为理想的均衡。
然后,为了获取信号的分量结构研究了信号的瞬时频率估计算法,研究发现已有算法不适用于存在交叉分量的信号,因此引入了梯度旋转方法来增强时频分布图像,并提出了基于端点梯度的片段连接和拟合算法,不仅消除分量瞬时频率跟踪错误,也降低了估计误差。
最后,在瞬时频率估计的基础上采用时变滤波方法提取和重建各个分量信号,分析发现时变滤波在分量交叉处存在较大的畸变,因此引入幅度校正算法并提出基于时变阶的短时分数阶傅立叶变换时变滤波算法。所提算法大幅度的提升了信号提取和重建的准确性,特别是针对非线性调频信号的提取和重建。论文针对多
分量信号时频分析中存在交叉项干扰与信号项模糊相矛盾问
题,引入了自适应方向核的时频分布算法获得了较理想的时频分布图像。进一步在该图像上使用旋转梯度增强和瞬时频率连接拟合算法,取出了各分量的瞬时频率。最后采用基于时变阶的短时分数阶傅立叶变换的时变滤波算法,提取并重建出各个分量的时域波形。将信号的提取和重建分解为信号建模、时频分析、瞬时频率提取和时变滤波四个步骤进行,形成了一套完整有效的多分量雷达信号提取和重建的方案。
关键词:时频分析;信号分离;时变滤波;短时分数阶傅里叶变换;瞬时频率
Abstract
With the increasingly complex electromagnetic environment in the battlefield, the intercepted radar signal is increasingly complicated. The complexity is reflected in the superimposed components which is modulated differently. To obtain the type and parameters of each component in the complex signals is the key factor of correct identification and efficient interference to each radiation source in strategic decision. To correctly analyze the intercepted multi-component radar signal, component extraction and reconstruction it is inevitable processes. This paper focuses on the extraction and reconstruction of multi-component signals based on the time-frequency representation (TFR) of signals.
Firstly, the time-frequency characteristics and sparse characteristics of radar signals are summarized. In addition, the laws of time-frequency analysis of multi-component radar signals is carried out. The inevitable balance between the interference suppression and signal fuzzification in the time-frequency analysis is found. Thus the adaptive direction quadratic TFR is introduced by adaptively selecting the optimal ambiguity domain direction kernel, the ideal equilibrium is achieved between interference suppression and signal fuzzification.
Secondly, in order to obtain the component structure of the signal, the instantaneous frequency (IF) estimation algorithm of the signal is studied. It is found that the existing algorithms may be wrong when the cross component exists. Therefore, the gradient rotation method is introduced to enhance the TFR image, and then a connection method based on endpoint gradient and curve fitting is proposed. Not only the IF tracking error of the component is eliminated, But also the estimation error is reduced.
Finally, based on the estimated IF, the time-varying filtering method is used to separate and reconstruct the individual compon ent. It is found that the time-varying filtering has large distortion at the intersection of the components. Therefore, the amplitude correction algorithm is introduced and a time -varying filtering algorithm based on time-varying order Short-time Fractional Fourier Transform is proposed. The proposed algorithm significantly improves the signal separation and reconstruction performance, especially for the nonlinear frequency modulated signal.
In this paper, the adaptive direction TFR algorithm is obtained to deal with the contradiction between cross-term interference and signal-term ambiguity, which achieved a relatively ideal TFR. Then the enhancement algorithm based on rotated gradient and segment connection followed with curve-fitting are proposed to overcome the track error of IF estimation. Finally, a time-varying order Fractional Fourier Transform based time-varying filtering algorithm is proposed to reconstruct the time domain waveform. This paper decomposes the signal separation and reconstruction into four steps: signal modeling, time - frequency analysis, IF extraction and time-varying filtering, which constitutes a complete and effective multi-component radar signal separation and reconstruction scheme.
Keywords: time-frequency analysis, signal decomposition, time-varying filte- ring, short-time fractional fourier transform, instantaneous frequency
摘 要 I
ABSTRACT II
第 1 章 绪 论 1
1.1 课题来源及研究的背景和意义 1
1.2 国内外研究现状及分析 2
1.2.1 非平稳信号的时频分析方法研究现状 2
1.2.2 瞬时频率估计方法研究现状 4
1.2.3 多分量信号的提取和重建方法研究现状 6
1.3 本文主要研究内容 8
第 2 章 多分量雷达信号建模及分析 10
2.1 引言 10
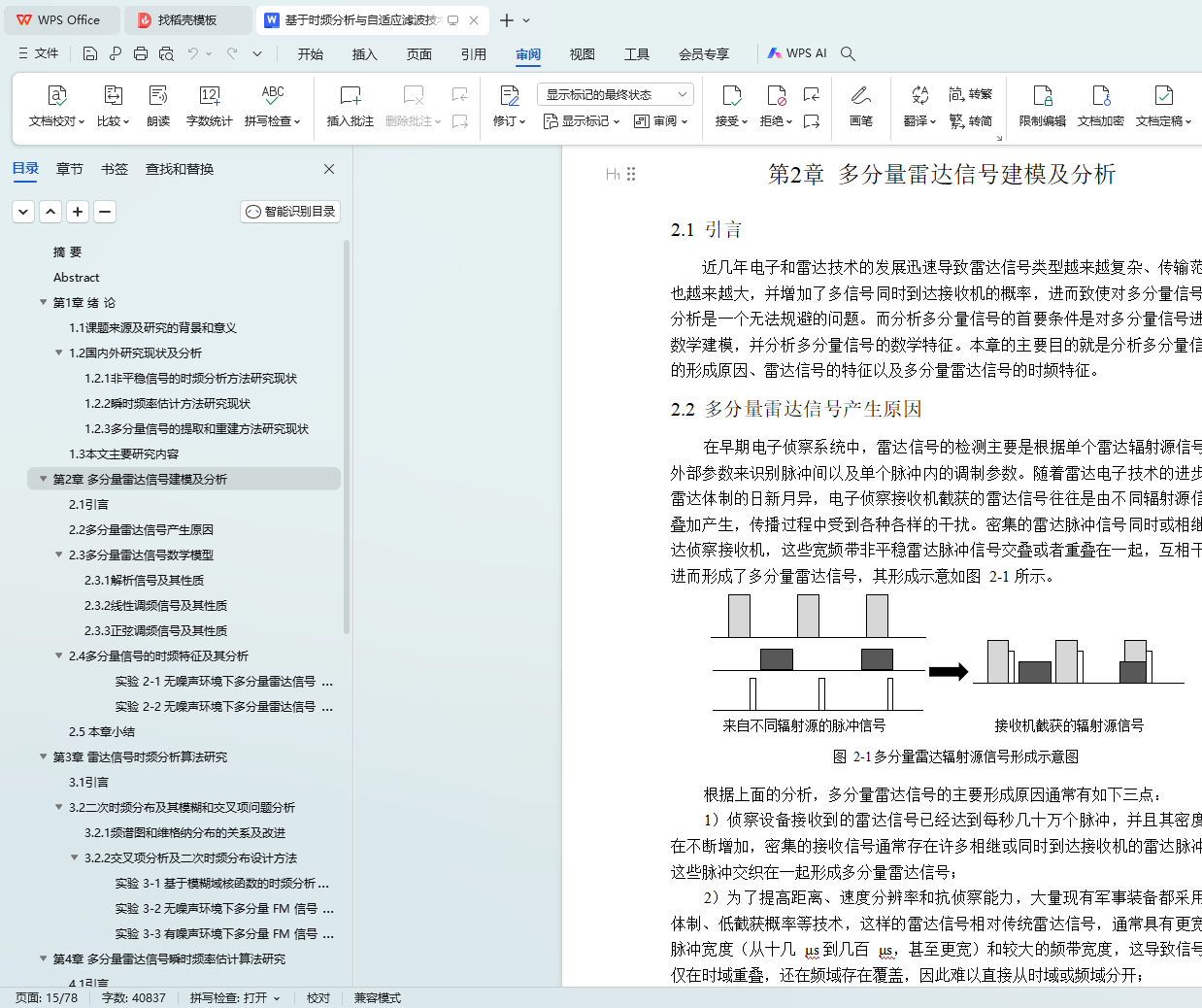
2.2 多分量雷达信号产生原因 10
2.3 多分量雷达信号数学模型 11
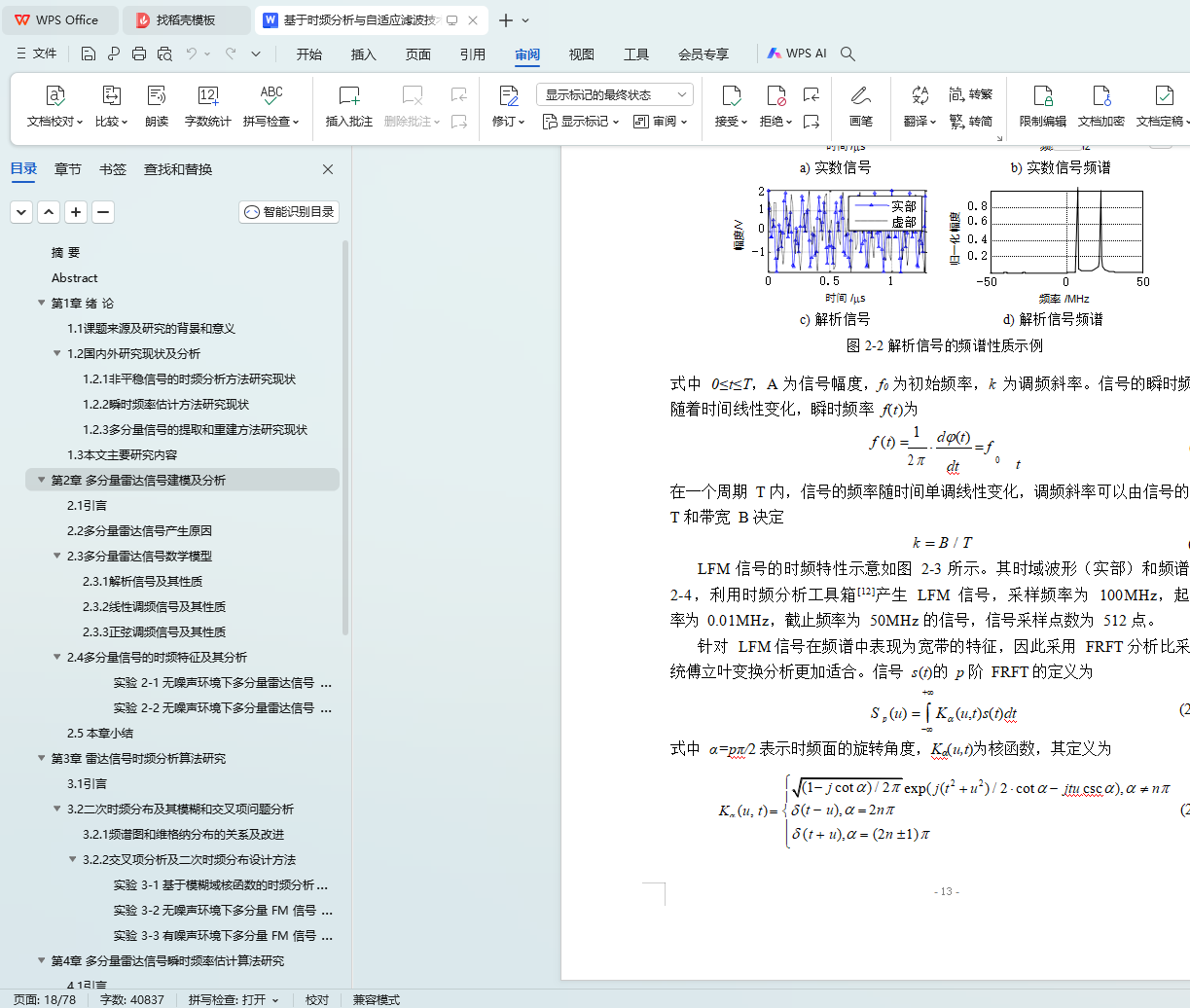
2.3.1 解析信号及其性质 11
2.3.2 线性调频信号及其性质 12
2.3.3 正弦调频信号及其性质 15
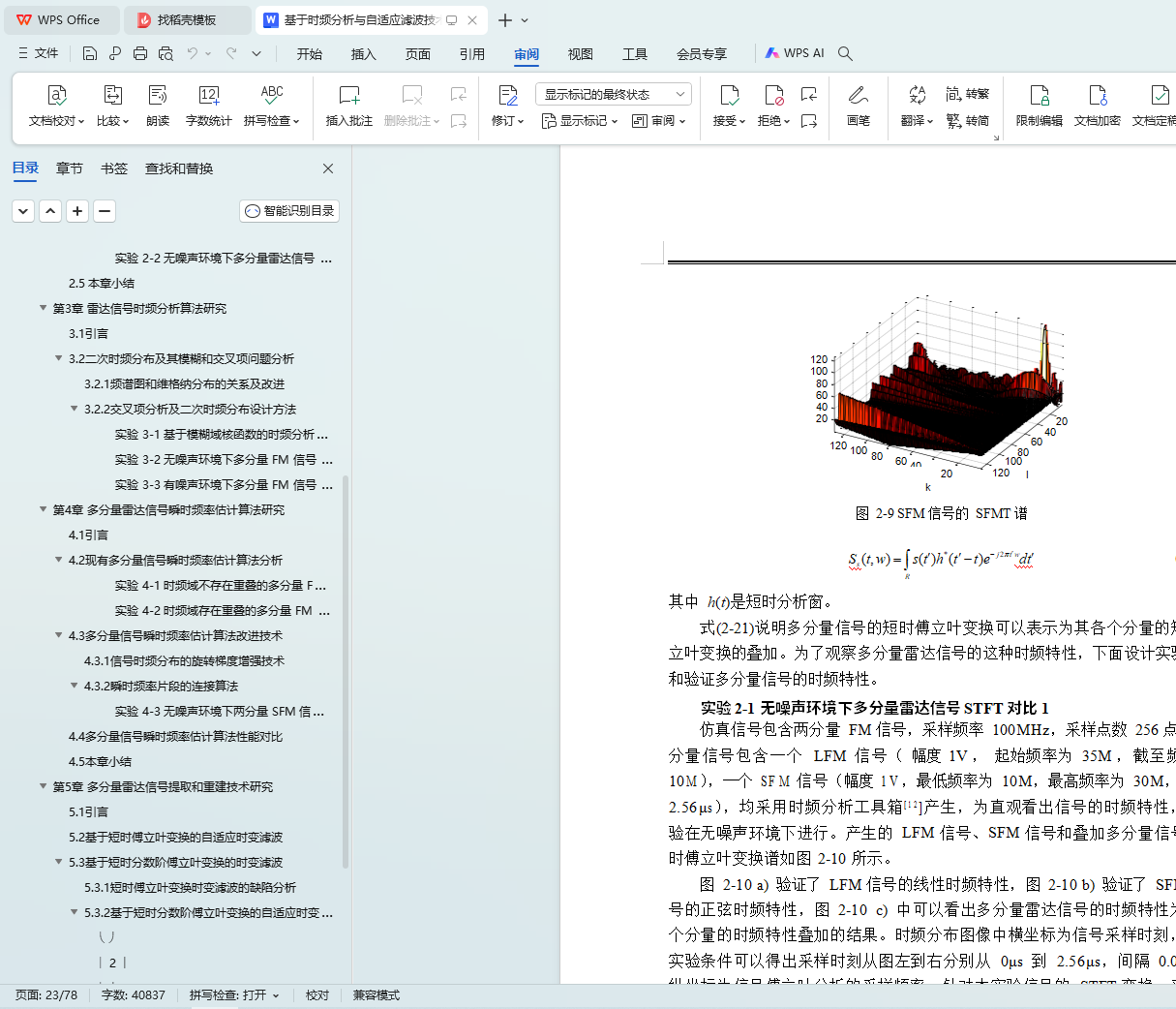
2.4 多分量信号的时频特征及其分析 17
2.5 本章小结 20
第 3 章 雷达信号时频分析算法研究 21
3.1 引言 21
3.2 二次时频分布及其模糊和交叉项问题分析 21
3.2.1 频谱图和维格纳分布的关系及改进 21
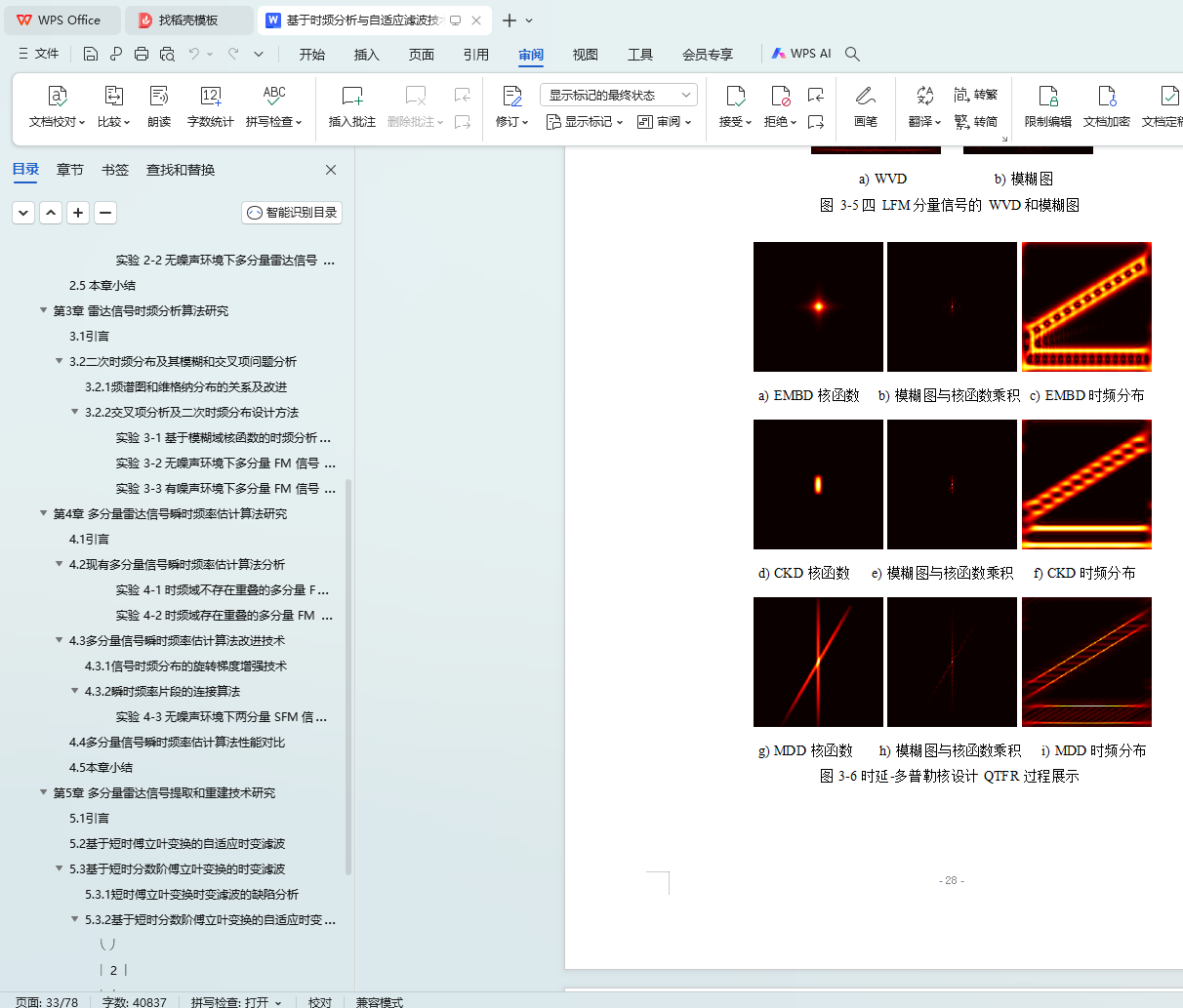
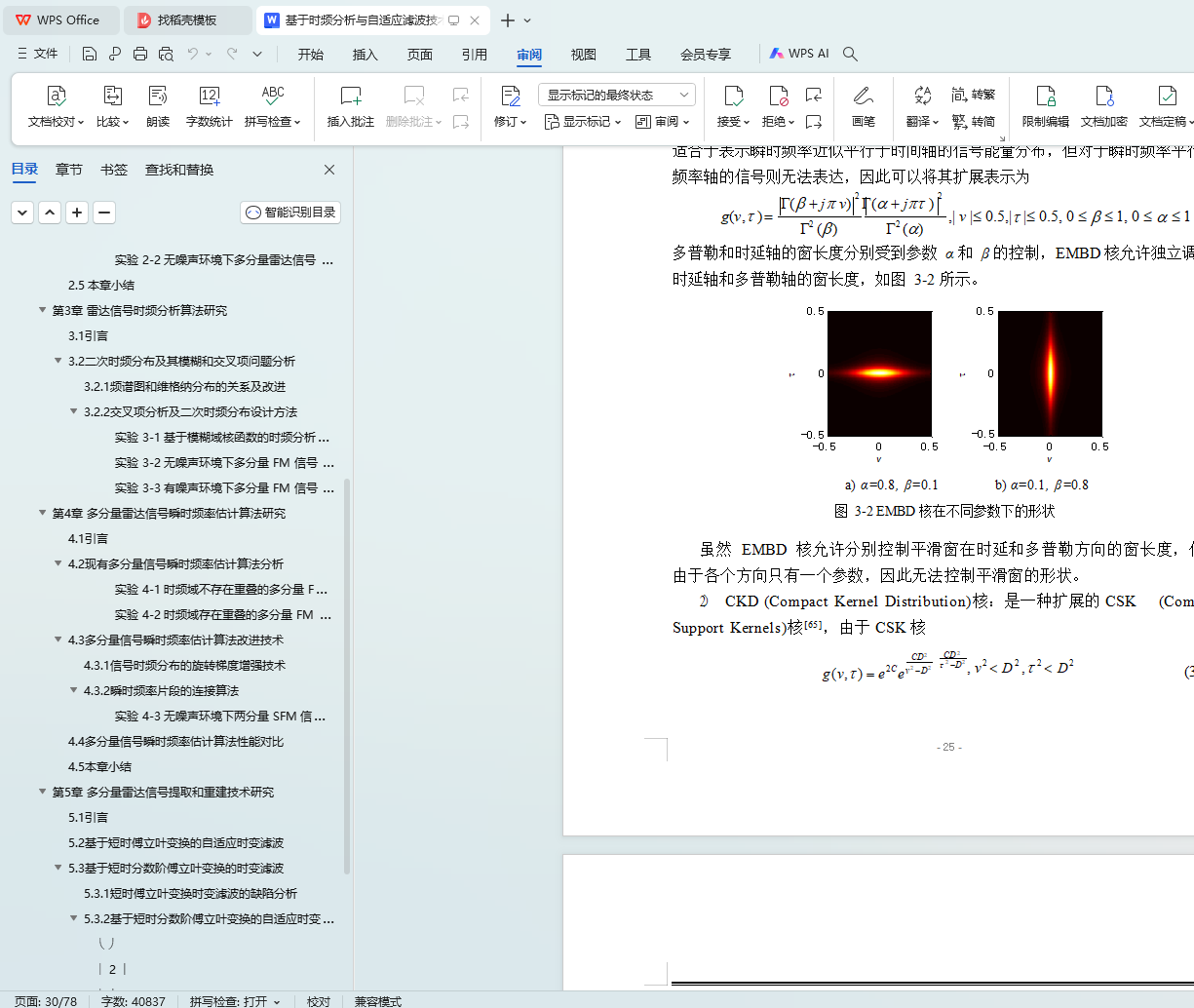
3.2.2 交叉项分析及二次时频分布设计方法 23
3.2.3 二次时频分布的性能评价指标 29
3.3 自适应角度二次时频分布算法 29
3.4 二次时频分布算法性能仿真 32
3.5 本章小结 34
第 4 章 多分量雷达信号瞬时频率估计算法研究 35
4.1 引言 35
4.2 现有多分量信号瞬时频率估计算法分析 35
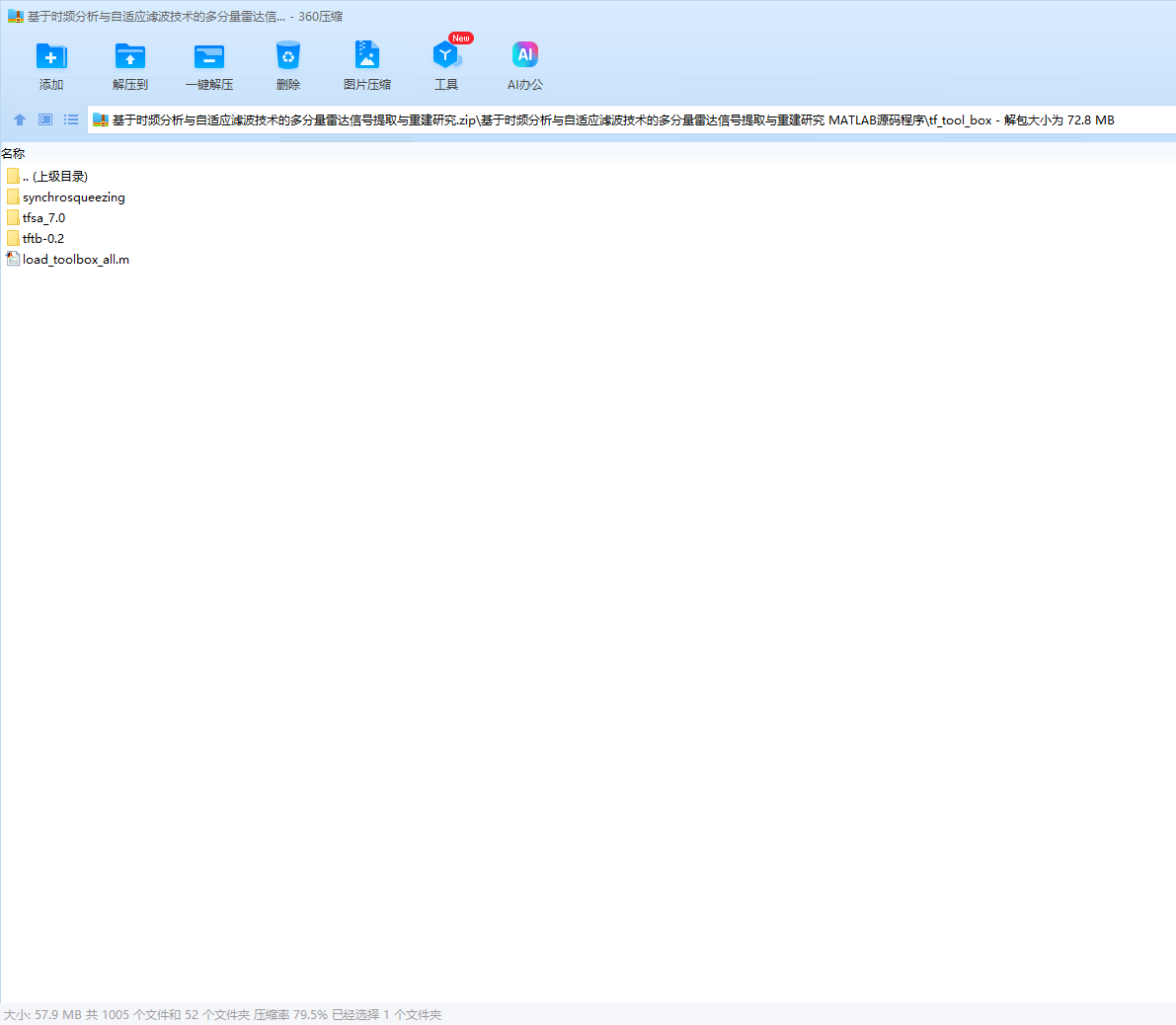
4.3 多分量信号瞬时频率估计算法改进技术 38
4.3.1 信号时频分布的旋转梯度增强技术 38
4.3.2 瞬时频率片段的连接算法 41
4.4 多分量信号瞬时频率估计算法性能对比 44
4.5 本章小结 45
第 5 章 多分量雷达信号提取和重建技术研究 46
5.1 引言 46
5.2 基于短时傅立叶变换的自适应时变滤波 46
5.3 基于短时分数阶傅立叶变换的时变滤波 49
5.3.1 短时傅立叶变换时变滤波的缺陷分析 49
5.3.2 基于短时分数阶傅立叶变换的自适应时变滤波 54
5.4 信号提取和重建算法性能对比 57
5.5 本章小结 61
结 论 62
参考文献 64
致 谢 73