1.各位老师好，我叫xx，指导老师为xx，我的答辩题目为xx

2.答辩内容分四个部分展开叙述

3.首先是研究背景与意义

4. 互联网用户规模的日益增长产生了庞大的数据量，据IDC预测到2025年我国数据总量将达到48.6ZB。关系型数据库由于关系定义严格、水平扩展能力较差无法满足需求。为了有效应对海量数据的存储与查询， 分布式数据库NoSQL逐渐兴起。HBase是NoSQL的杰出代表，但是它不支持基于非主键的多维查询。

然而，在许多应用场景下，基于非主键的多维查询是一种常见的需求。且在分布式集群上创建多维索引是一个复杂的问题，需要考虑到跨节点的数据分布和索引维护的成本。因此，提出一个简单易用、查询效率高的HBase多维索引结构具有重要的现实意义。

5. 接下来是研究现状与问题分析

6. 我们将索引方案分成三类：分别是二级索引、双层索引和基于线性化技术的索引。

二级索引结构简单、维护成本低，但在执行多维查询时效率较低，同时会占用较多的存储空间。

双层索引具有较好的拓展性，但是索引实现复杂，更新索引代价较高。

7. 基于线性化技术的索引具有较高的写入吞吐量和较低的维护成本，较前两种方案具有更好的插入和查询效率，本文基于这一方案开展研究。

8. 接下来是问题分析。存在的问题有：单一空间填充曲线无法良好适配多维查询的需求、对倾斜数据的查询缓慢和无法兼顾数据并发和高吞吐量。

针对这些问题，本文的研究思路是1.提出一种新的空间填充曲线，更好的服务于多维查询。2.建立辅助索引层，分配更多资源对倾斜数据进行查询。3.使用流计算技术支持数据并发，提高数据吞吐量。

研究目标为：1.提出一种具备优良性质、能够优化查询的混合空间填充曲线。2、在HBase之上建立查询优化、支持高性能插入的多维索引。3、设计这一多维索引的范围查询和KNN查询算法。

9. 本文的研究创新点有三条，一是提出了一种新的二分混合空间填充曲线，二是提出了一种基于流式批处理计算的HBase多维索引结构SFI-HBase。三是为SFI-HBase设计范围查询和KNN查询算法。

10. 接下来是研究内容

11. 空间填充曲线具备一些理论性质，包括局部性和聚集度。常见的Z曲线在局部性和聚集度均劣于Hilbert曲线。

自相似特性是指曲线的部分和整体之间存在着相似的结构。划分性质是指曲线裁剪多维空间的能力。Z曲线支持二分划分，而Hilbert曲线不支持二分划分。

因此，我们提出了二分混合空间填充曲线的概念，将二分划分特性与优良局部性、聚集度特性相结合起来。

12. 二分混合空间填充曲线的定义为：对一个m维n阶的欧几里德空间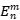，如果能够通过可变阶数值x划分阶数，使得高阶曲线H和低阶曲线L分别在高阶和低阶编码后的图像铺满该空间，则该图像为一个二分混合空间填充曲线。

它运用于多维索引有如下优点，包括支持二分划分多维空间，具有更优的理论性质和支持动态增加阶数。

13. 接着介绍二分混合空间填充曲线的编解码算法和时空复杂度分析，编码方法首先基于可变阶数值x对输入的多维数据点划分阶数，然后使用H和L分别划分的结果进行编码，最终合并得到编码结果，解码算法是编码算法的逆运算。

二分混合空间填充曲线的时空复杂度基于其组成曲线，取H与L中复杂度较高的那个曲线，第二个参数转变为可变阶数x或n-x。

14. 我们通过定义理论指标对多维查询效率进行衡量，包括：平均/最坏情况下的局部性、边界框面积比、边界框平方周长比和聚集度。

右图展示了一个矩形区域的指标计算示例，接着对这些理论性质进行实验对比。

15. 在图中的条件下，在每个维度、曲线和查询边长的组合下进行500次随机计算，取500次计算中指标的最大值作为最差指标，平均值作为平均指标。最终局部性、聚集度指标的实验结果如图所示。

16. 我们通过一个排序表格对实验进行总结，Hilbert曲线在所有曲线中拥有最好的理论性能，但是它不支持二分划分，在其余支持二分划分的曲线中，Blend_Z_Hilbert曲线具有综合最好的理论性质，因此我们选用该曲线作为本文多维索引的线性化方法。

17. 接着开始介绍流式全量索引SFI-HBase ，首先是问题描述。

GeoMesa和MD-HBase是两种典型的索引结构，GeoMesa查询构建速度较快，但是对倾斜数据的支持较差。MD-HBase对倾斜数据查询效率高，但是辅助索引表维护代价高，且不支持并发插入。

18. 基于GeoMesa和MDHBase，我们提出了流式全量索引SFIHBase。

其优点包括：支持索引桶的快速拆分、对并发插入的支持和多粒度查询优化。

19. 接着介绍SFI-HBase结构的存储结构。在图中的条件下，全量索引层包含16棵k-d树,存储二进制前缀和桶数据量大小两列。存储层为避免数据点主键重复加入了4个bit长度的UUID,包括维度值列和其他数据列

20. 范围查询是在指定范围内检索数据的一种方式。

SFI-HBase的范围查询分为两个步骤：1.根据范围查询条件设置最佳查询桶大小。2.根据最佳查询桶大小计算索引信息，并根据索引信息向存储层查询数据。

21. KNN查询的目的是找到距离多维数据点最近的K个点。

SFI-HBase的KNN查询分为两个步骤1.找出能够满足查询数量K的索引桶2.从这个索引桶中进行搜索，并判断是否满足查询结果，若满足返回，否则执行基于索引块排序的KNN查询。

22. 接下来是实验部分。我们在3、4、5三个维度下设计了SFI-HBase与多个系统的插入、范围查询、knn查询的对比实验。右图为服务器的配置信息。

23. 插入实验对比了SFI-HBase与其他系统在不同维度下的插入效率。插入时间对比如图所示。除原生HBase和GeoMesa没有辅助索引表插入时间更短外，SFI-HBase具有最好的插入性能。

24. 接着是范围查询实验结果。

在3/4/5三个维度下，SFI-HBase具有各个选择率下相对最佳的范围查询效率。

25. 最后是KNN查询实验结果。

在三个维度下，SFI-HBase均具有各个K值下相对最佳的KNN查询效率。

26. 为了验证SFI-HBase在真实场景下使用的可行性，我们基于开放数据实现了一个网约车离线分析平台。

系统架构有四个分层，分别为 数据采集层、存储计算层、接口层和应用层。

系统功能模块共包含七个模块，其中数据同步和订单查询模块为本文关键模块，运用了前文所提到的SFI-HBase索引结构。

27. 然后是关键模块流程，数据同步模块定义了JDBC到SFI-HBase的数据同步流程，订单查询模块定义了向SFI-HBase请求数据的流程。

28. 系统的部分界面展示如图所示

29. 最后是系统的演示

30. 最后是总结与展望

31. 本文首先提出一种结合了二分划分与优良局部性、聚集度的二分混合空间填充曲线，并给出了它的编码解码算法。其次，提出了一种基于流式批处理计算的HBase多维索引结构SFI-HBase，并为其设计了高效的范围、KNN查询算法。最后，基于开源网约车数据集实现了一个网约车离线分析平台。

32. 最后是展望部分：包括三个点，1是研究更多性质优良的空间填充曲线，以期通过结合获得理论性质更优的二分混合空间填充曲线。二是提出一种耗时短、精准度好的计算最佳桶大小的算法。三是为SFI-HBASE设计编写离线同步模块。

33. 以上是我的答辩内容，请各位老师批评指正