古塔的变形

摘要

本文要求根据测绘公司对古塔的 4 次测量数据，给出确定古塔各层中心位置的通用方法，并分析古塔的变形情况及其变形趋势。为了计算的精度，我们首先对各变形量进行了合理的数学定义，并对附录的缺失数据进行合理的赋值。

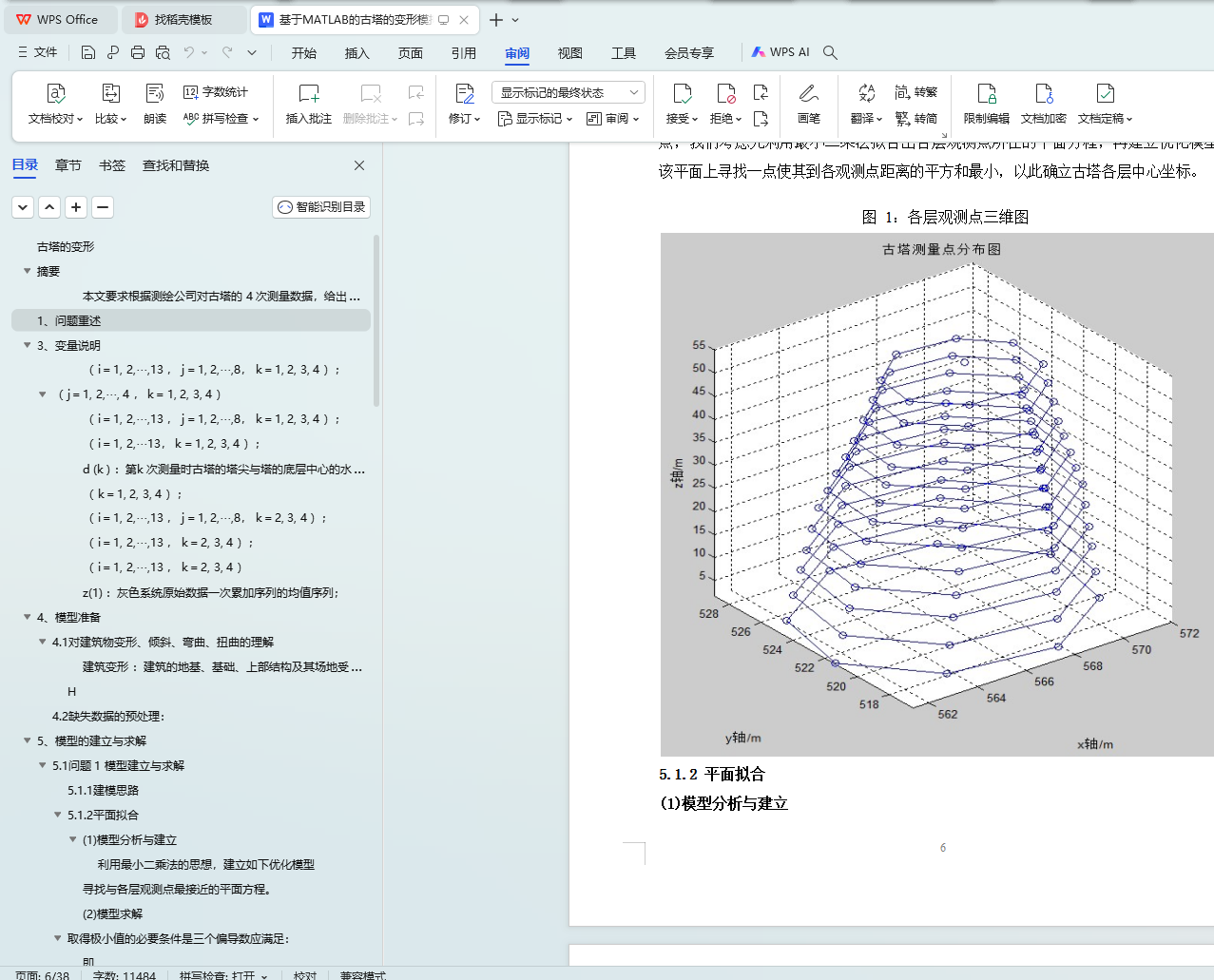
对于问题一，我们通过最小二乘法拟合出观测点所在平面，再建立优化模型，在拟合平面上寻找到各观测点距离的平方和最小的点作为古塔该层的中心点。利用 MATLAB 编程求解，得到了每次观测古塔各层中心坐标的通用方法及各层的中心点坐标。

对于问题二，我们将古塔的倾斜、弯曲和扭曲等变形情况，分别给予合理的数学描述。对于倾斜变形，我们定义了倾斜角a，即塔尖与底层中心的水平距离与塔高的比值； 对于弯曲变形，我们定义了弯曲率 K ，即用中心点所拟合出的空间曲线的曲率来描述古塔各处弯曲率；对于扭曲变形，我们定义了相对扭曲度q，利用坐标的旋转变换角度描述古塔的扭曲变形情况。利用空间曲线拟合、坐标变换等方法以及 MATLAB 程序，分别求出了三个变形刻画量的量化指标。

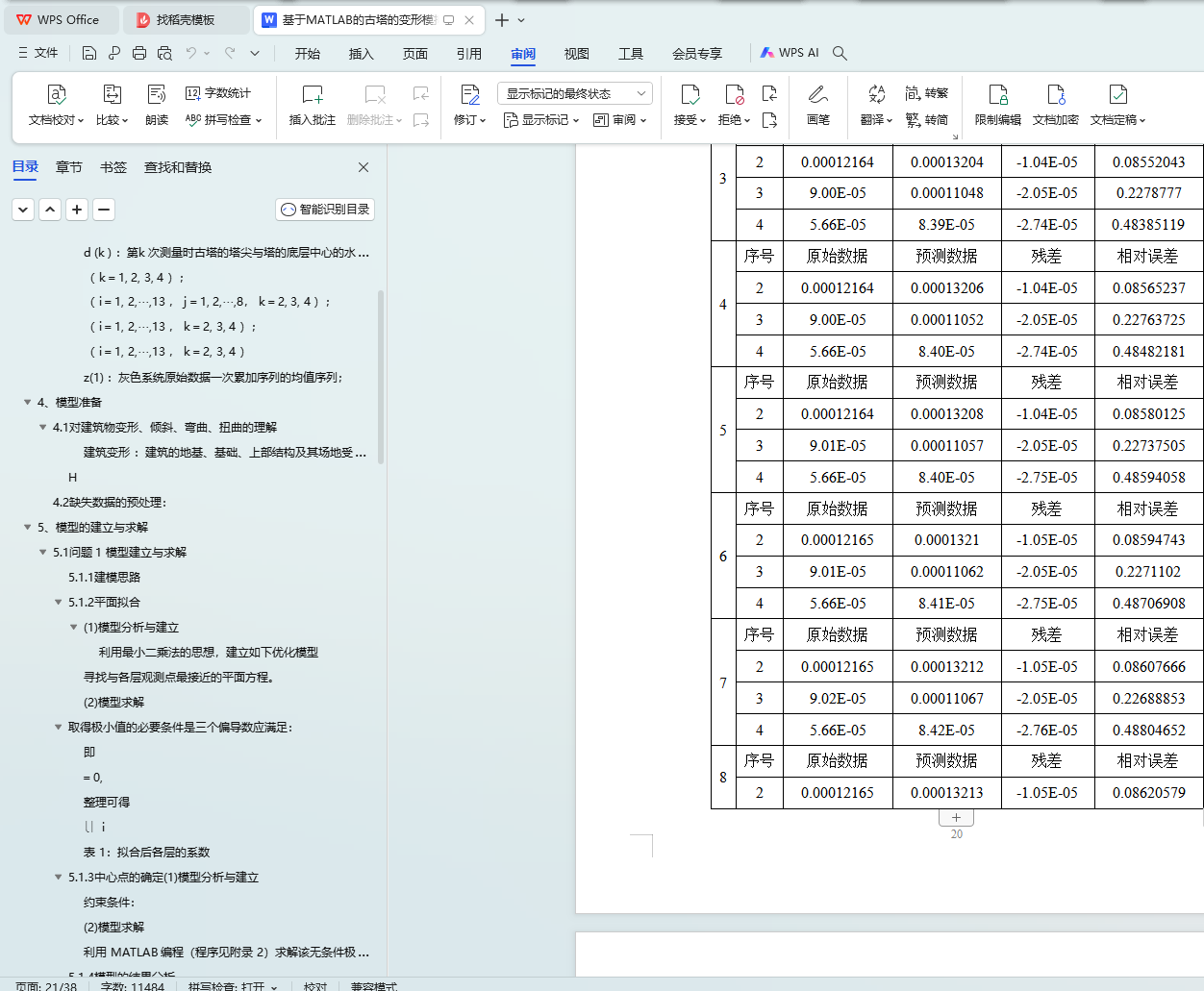
对于问题三，我们考虑通过古塔的倾斜、弯曲及扭曲程度来分析古塔的变形趋势。由于数据量较少，我们建立灰色预测模型分析这三种变形因素的变化趋势，利用相应的

MATLAB 程序，得到了倾斜角、弯曲率以及相对扭曲度的预测函数和误差检验，验证了模型的可靠性，并继而分析古塔的变形趋势。

本文巧妙地将各种变形量给予了合理的数学描述及模型，并运用最小二乘法、曲线投影拟合、坐标变换等数学方法实现了求解，并利用灰色预测对未来变形趋势进行了预测，具有较好的实用性和可推广性。

关键词：古塔变形；最小二乘拟合；空间曲线曲率；坐标矩阵变换；灰色预测；