基于统计分析的公共自行车服务系统评价模型研究
摘要
本文针对温州市鹿城区公共自行车管理中心提供的数据，首先对所给数据进行预处理，建立了相关统计模型，运用SPSS20.0、matlab等软件进行统计分析，最后应用关联度分析法对系统进行评价，并提出改进建议。
针对问题一：在已处理好的数据基础上，建立了频率与频数、用车时长的统计模型，利用SPSS软件分别统计各站点20天中每天及累计的借车及还车频次，得到每天和累计的借车和还车频次（见表五和表六）；并对所有站点按累计的借车和还车频次排序（见表七和表八）；对每次用车时长的分布情况进行统计分析，画出其分布图（见图一和图二），由图可知：每天用车时长分布形状非常相似且近似服从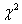
分布。
针对问题二：在已处理好的数据基础上，建立了使用公用自行车的不同借车卡数量的统计模型,利用SPSS统计20天中每天使用不同借车卡数量，其中最大的为第20天的19885；统计了每张借车卡累计借车次数的分布图（见图三），对图形分析可得：借车次数在10次以内的占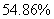
，借车次数在10至30次占
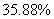，借车次数在30至50次占
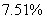，借车次数在50以上占
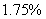，最大借车次数高达
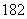次。
针对问题三：根据问题一的分析，已给站点累计所用公共自行车次数最大的一天是第20天。对于第一小问：利用第20天数据，运用floyd算法求得两站点间最短时间，将站与站间的距离定义为两站间的最短时间与自行车速度之积，同时考虑到了速度和时间的随机误差影响；利用距离的定义，通过matlab计算得两站点最长距离为：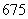
，最短距离为:
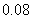。利用问题一中的频数模型,对借还车是同一站点且使用时间在１分钟以上的借还车情况进行统计，得借车频次表（见表十一）和用车时间分布图（见图四）。对于第二小问:根据问题一的统计，第20天的借车和还车频次最高的站点分别为42（街心公园）和56（五马美食林），利用SPSS统计出两站点借、还车时刻和用车时长的分布图（见图五，图六，图七），由图形分析可知：借还车的高峰期与人们上下班的时间非常吻合，在借还车时间上大体都在一小时以内。第三小问:将第20天数据从６点到22点每半小时作为一时段，分别统计各站点各时段借还车频数，利用matlab编程求出借还车高峰时段（见表十二），并对具有借车高峰时段与还车高峰时段的站点进行归类。（见表十四）
针对问题四：根据前三个问题的统计结果，结合公共自行车服务指南，确定评价公共自行车服务系统站点设置和锁桩数量的配置的主要指标有：借车频数、还车频数、可借比例、可还比例、锁桩数目，建立了基于灰色关联分析法和聚类分析的公共自行车服务评价模型，得到评价结果：180个站点分成有优劣之分的三个类（见表十五）。
针对问题五：通过查阅相关资料知：公共自行车的其他运行规律主要是借还车时间有限制，用车时间集中在短时间内等。针对此问题提出了相关建议。
关键词：公共自行车服务系统 统计分析 灰色关联度分析 聚类分析
目录
基于统计分析的公共自行车服务系统评价模型研究
摘要
一、 问题重述
1.1问题背景
1.2问题提出
5. 找出公共自行车服务系统的其他运行规律，提出改进建议。
二、问题分析
2.4问题四分析
2.5问题五分析
五、数据预处理
六、模型的建立与求解
6.1问题一的解答
6.1.1模型一的建立
6.1.2模型一的求解
6.2问题二的解答
6.2.1模型二的建立
6.2.2模型二的求解
6.3问题三的解答
6.3.1模型三的建立
6.3.2模型三的求解
6.3.3 问题三（2）求解
6.3.4 问题三中（3）求解
6.4问题四的解答
6.4.1模型四的建立：
6.4.2模型四的求解
6.5问题五的解答
2. 在借车高峰时段，可能会存在无车可借，无桩可还的情况
七、模型评价与推广
7.1模型的优点
7.2模型的缺点
7.3模型的推广
八、参考文献
附录2：各站点20天中每天及累计的借车频次和还车频次
附录3：各天及累计用车时长频次分布图
附录4：计算两站点之间的最小时间（程序3_1）
for j=i:181
if x(i,j*2-1)~=0
附录7：各站点的借车高峰时段和还车高峰时段
附录8：高峰时段各站点的借车频次和还车频次
附录9：具有共同借车高峰时段和还车高峰时段的站点的分类
