题 目空间飞行器主动段轨道估计与误差分析
摘 要
本文通过微分方程组数值解法计算观测卫星的三维位置,在此基础上利用双星逐点交汇思路得到空间飞行器的轨道及残差估计,并对存在的三轴指向误差进行估计,最后给出单星观测的模型及多星观测的展望。
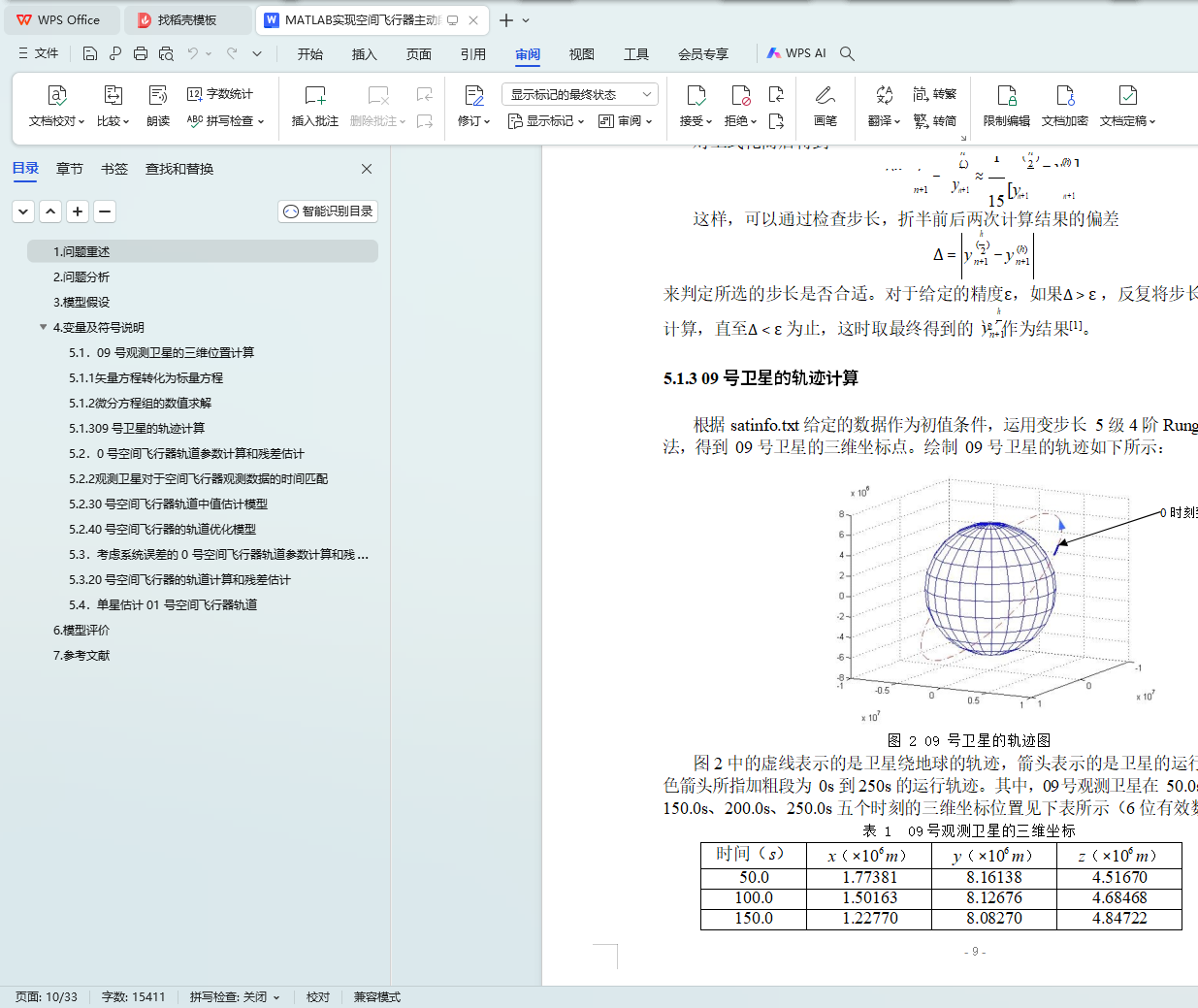
根据给定的观测卫星简化运动方程,利用惯性坐标系下 09 号观测卫星的位置和速度初值,使用变步长 5 级 4 阶 Runge-Kutta 算法求解常微分方程组,计算出 09 号卫星的绕地运行轨迹和速度,同理可以计算 06 号卫星的运行参数。
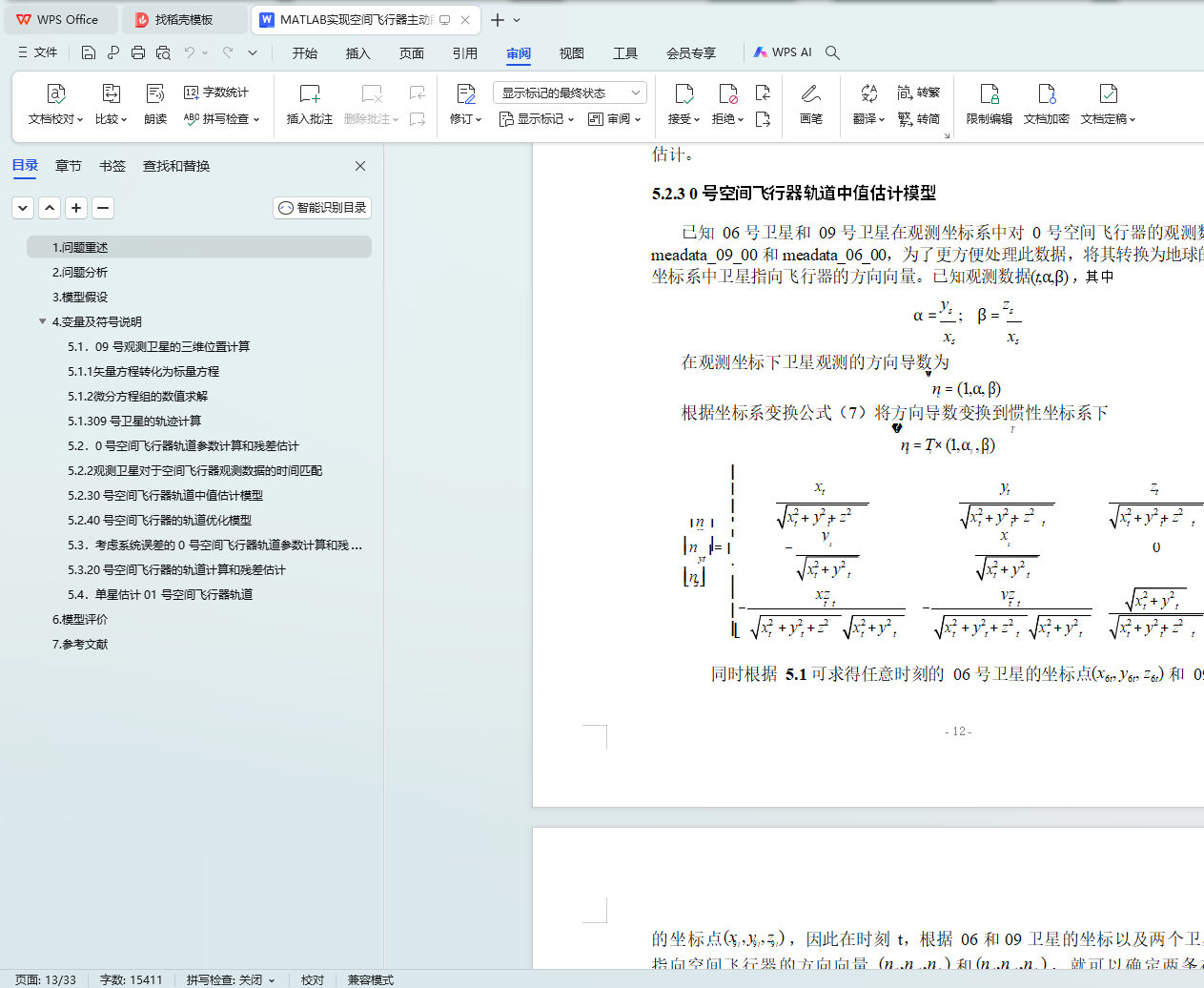
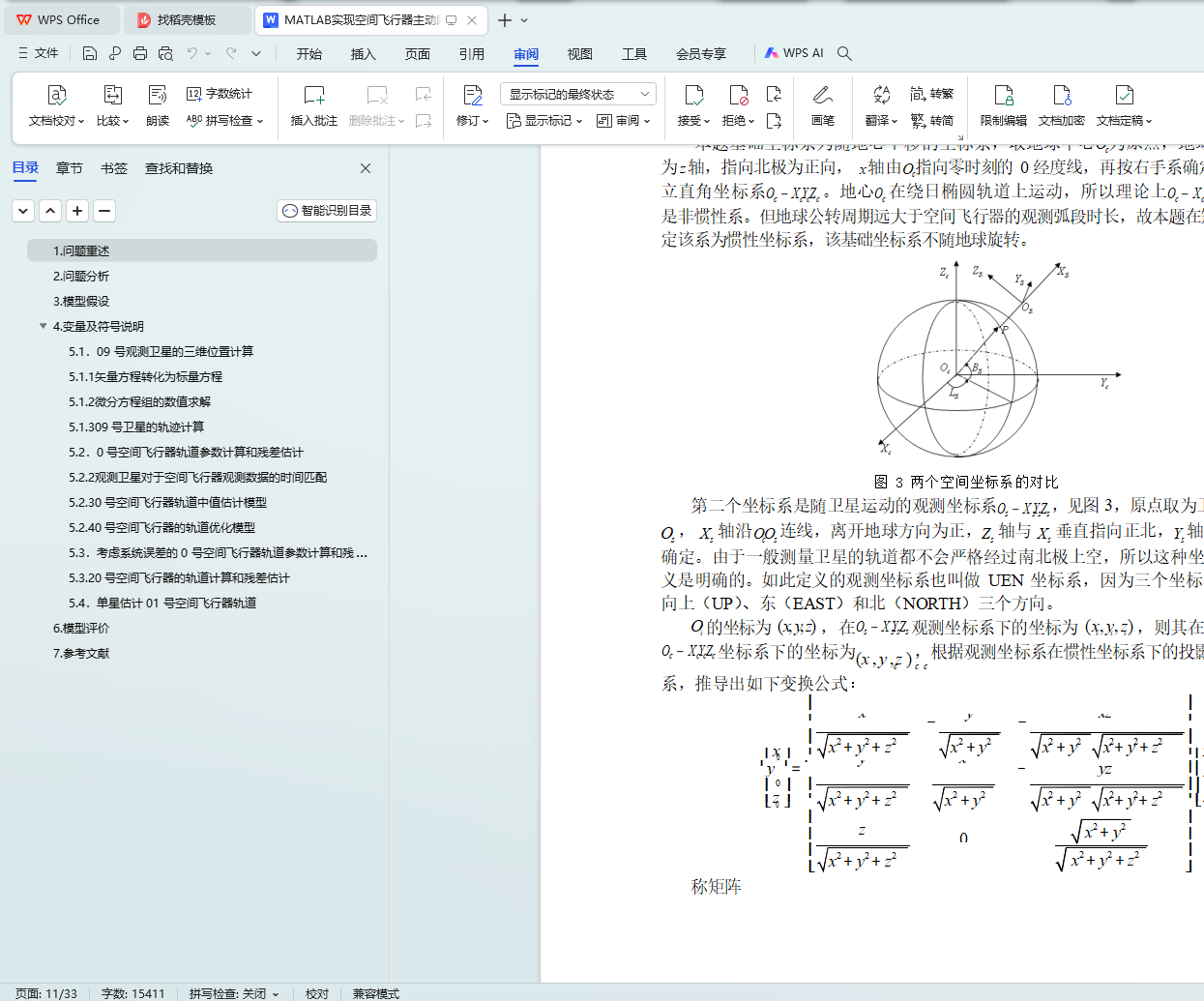
在计算 0 号空间飞行器参数的过程中,利用立体几何知识,推导出坐标转
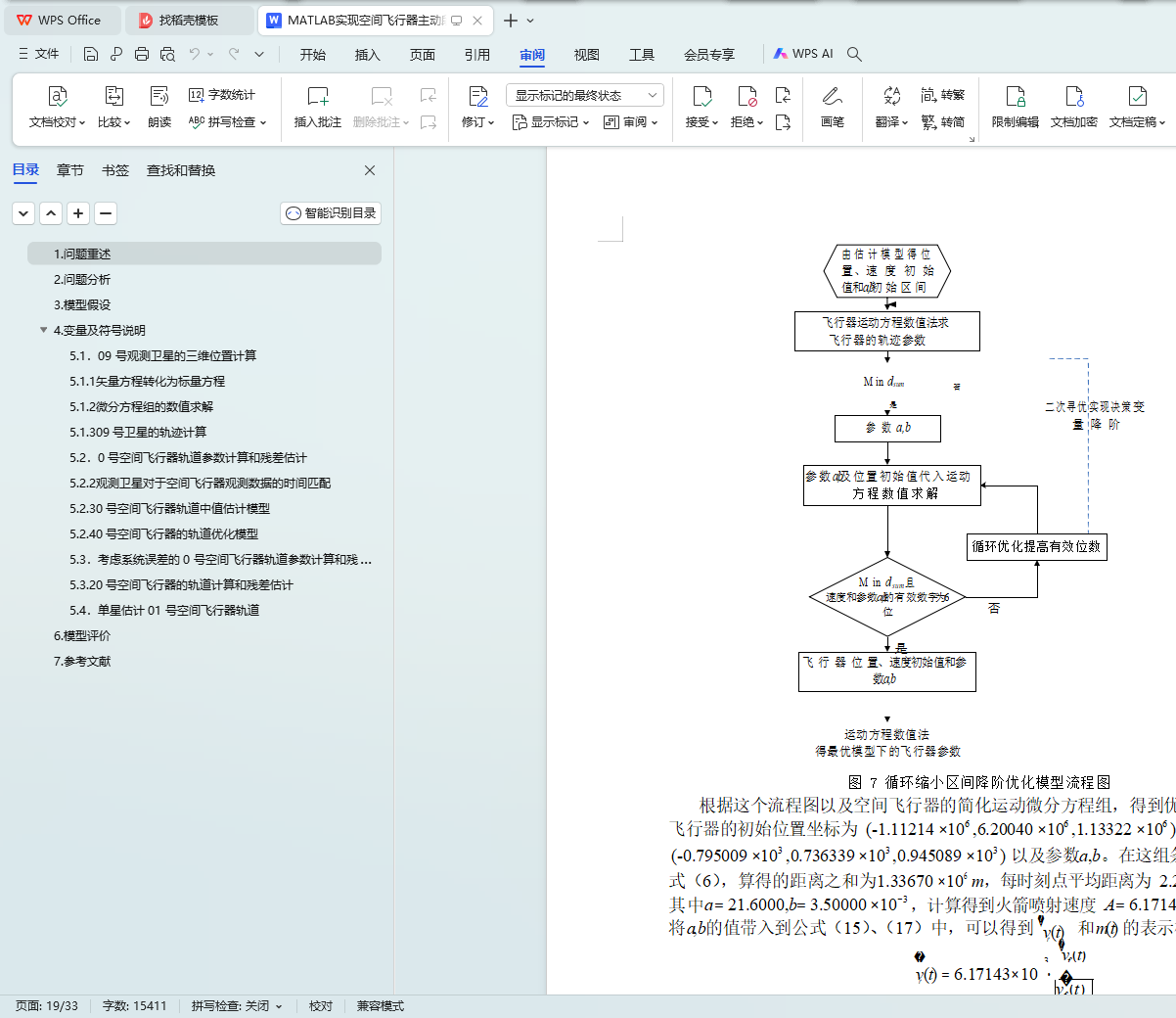
换矩阵T,将观测坐标系转化为地球惯性坐标系。文中建立了 0 号飞行器的两个轨迹模型:双星定位中值估计模型与双星定位优化模型。根据 meadata_09_00 和 meadata_06_00 得到双星观测飞行器的方向向量,并依据T 变换到惯性坐标系下,得到各个时刻下的两条异面直线,确立它们的公垂线段,用公垂线段的
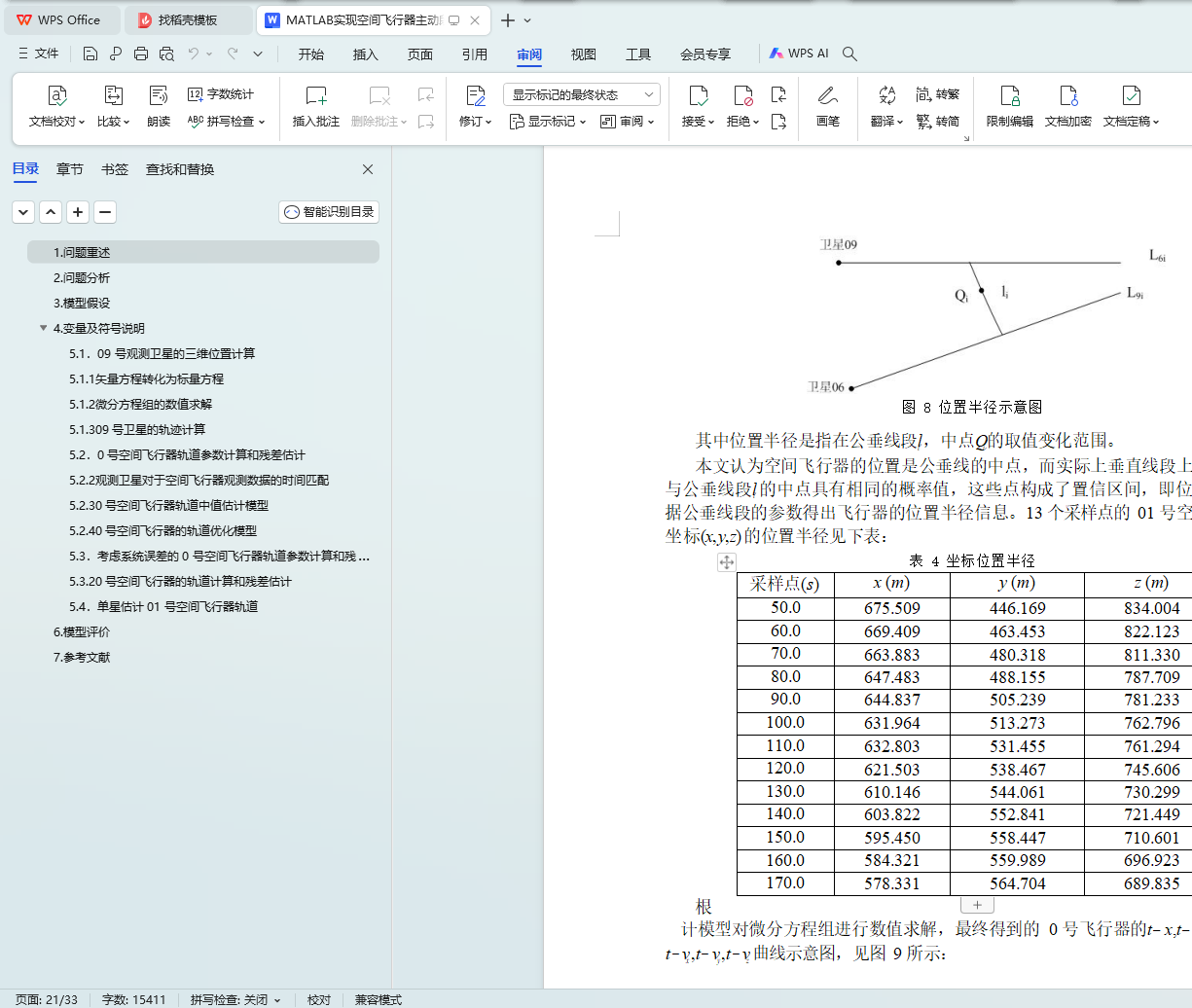
中点来建立空间飞行器轨道的中值估计模型,并给出此估计轨迹的位置半径作
�
为置信区间;建立vr(t) 大小稳定、方向变化的模型及
m(t)
单调递减的非负函数
模型,根据飞行器主动段简化运动方程,以飞行器空间轨迹点到两条异面直线
�
距离和最短来建立优化模型,对飞行器的速度及vr(t) 、
m(t)
的模型参数进行循
环降阶缩小区间算法优化,得到 50.0s、100.0s、150.0s、200.0s 以及 250.0s 五个 时 刻 空 间 飞 行 器 轨 迹 的 优 化 参 数 。 其 中 50.0s 时 刻 的 三 维 坐 标 为(1.77381×106 ,8.16138×106 ,4.51670×106 ) 。对比估计模型与优化模型求得的参
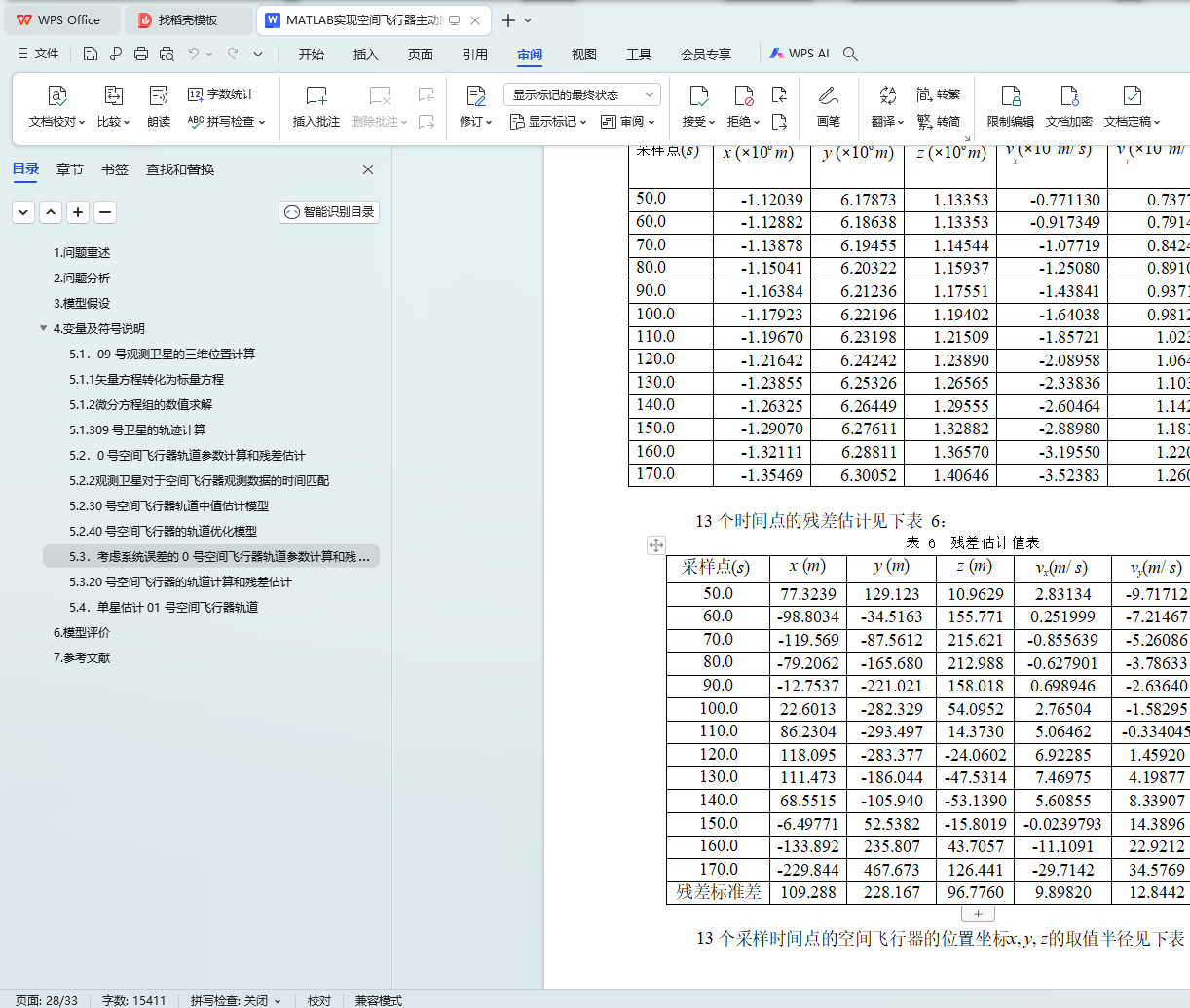
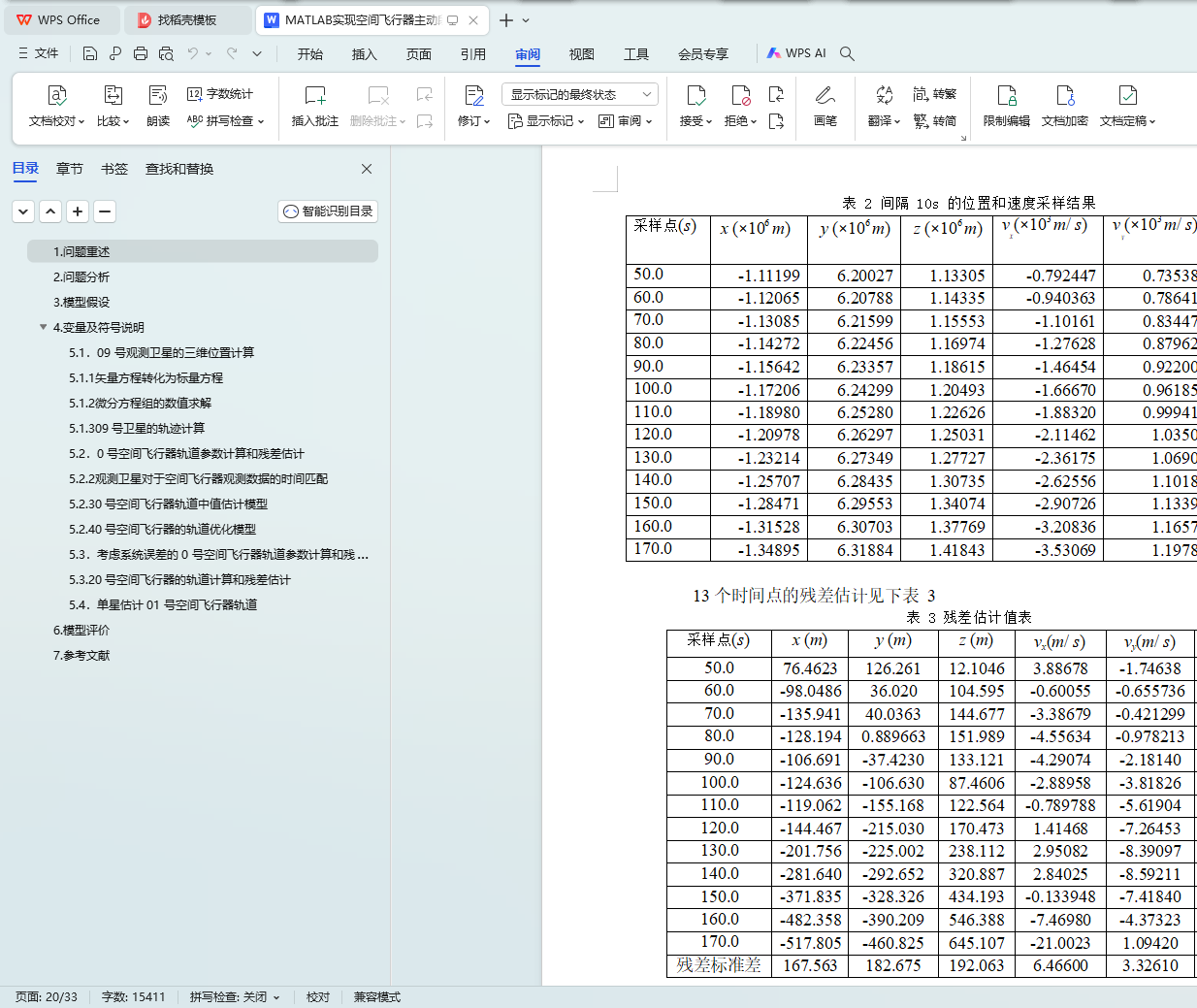
数,给出 13 个采样点的估计残差。
将双星测量定位过程中的系统误差(三轴指向误差) dα, dβ, dθ 带入到 0
号空间飞行器的轨道计算中,在双星观测飞行器的两条方向向量异面直线之间
最短距离的最小寻优下,得到两颗卫星的系统误差 dα, dβ, dθ 值。将求得的 dα, dβ, dθ 值代入双星定位中值估计模型与双星定位优化模型中,此为考虑系统误差下的飞行器轨迹与残差估计。根据计算,09 号观测卫星的系统误差为dα9 = 0.00309 , dβ9 = −0.00365 , dθ9 = 0.00033 ,06 号观测卫星的系统误差为 dα6 = −0.00425 , dβ6 = 0.00139 , dθ6 = 0.00293 ,并计算得到位置半径减小两 个数量级的更为精确的 0 号空间飞行器轨迹。
09 号卫星对 01 号空间飞行器进行单星定位时,首先根据卫星坐标以及其与空间飞行器之间的方向向量,确定一条包含飞行器的直线,再根据飞行器主动段简化运动方程确定一条空间飞行器的估计轨道,以同一时刻空间飞行器的轨迹点与其对应的方向向量的距离最优,实现空间飞行器的定位。
本文结合立体几何原理建立了两个模型用以估计飞行器的轨迹及残差,其中双星定位优化模型采用了循环缩小区间的算法和随机跳跃法达到了多决策变量降阶的目的,并提出位置半径作为考虑系统误差下模型精度提高的判断标准。
关键词:逐点交汇法,轨道估计,位置半径,循环降阶优化,三轴指向误
差
目录
1.问题重述
2.问题分析
3.模型假设
4.变量及符号说明
5.1 .09 号观测卫星的三维位置计算
5.1.1 矢量方程转化为标量方程
5.1.2 微分方程组的数值求解
5.1.3 09 号卫星的轨迹计算
5.2 .0 号空间飞行器轨道参数计算和残差估计
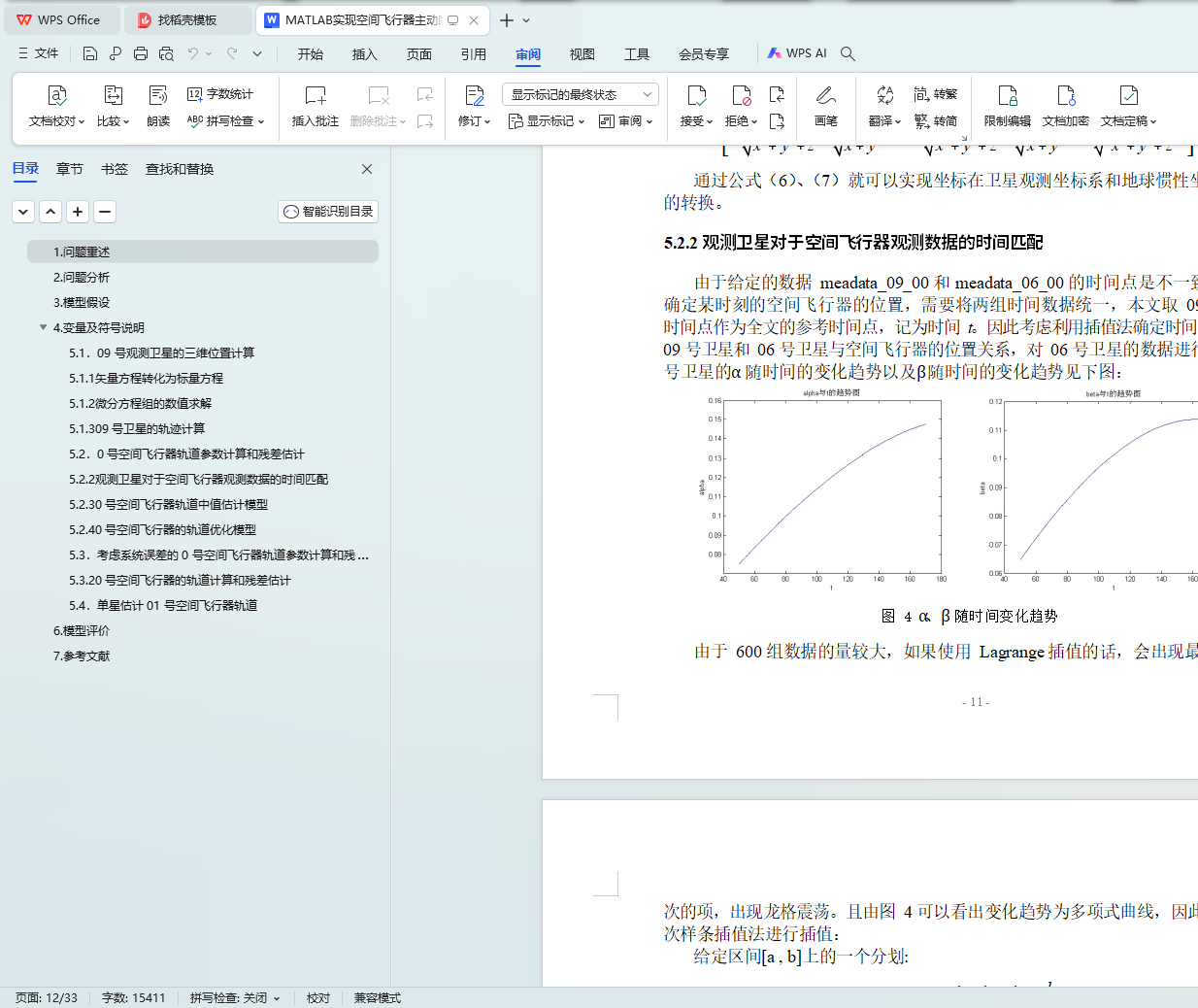
5.2.2 观测卫星对于空间飞行器观测数据的时间匹配
5.2.3 0 号空间飞行器轨道中值估计模型
5.2.4 0 号空间飞行器的轨道优化模型
5.3 .考虑系统误差的 0 号空间飞行器轨道参数计算和残差估计
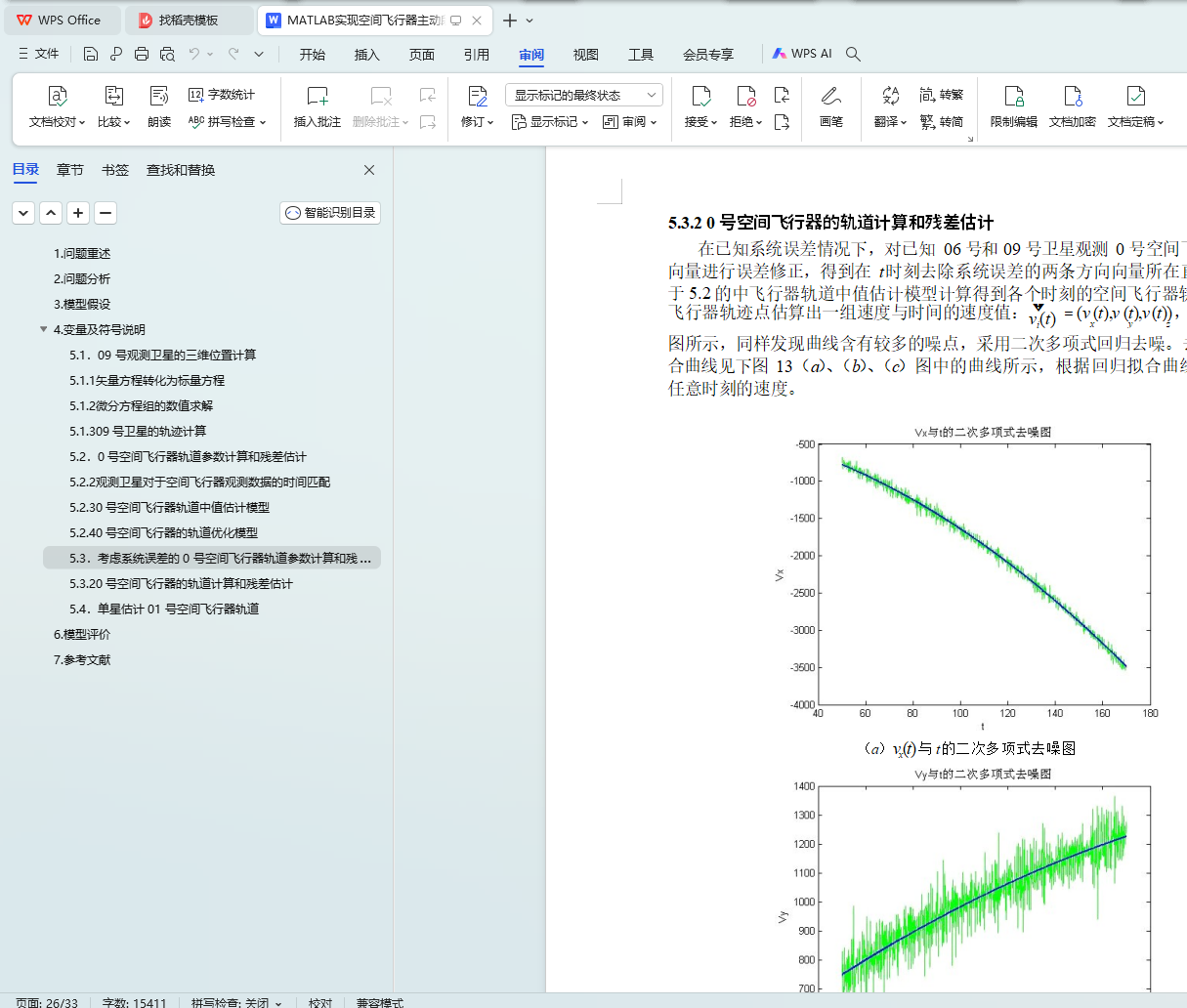
5.3.2 0 号空间飞行器的轨道计算和残差估计
5.4.单星估计 01 号空间飞行器轨道
6.模型评价
7.参考文献