微分方程的对称性和积分方法

Bluman G W¹, Anco S C²

1 英属（不列颠）哥伦比亚大学 温哥华 加拿大

2 布鲁克大学 圣凯瑟琳 加拿大

2 李变换群和无穷小变换

2.1 介绍

   在量纲分析中，基本维数的缩放（1.86），可测量物理量的诱导缩放(1.88)，所有物理量的诱导缩放(1.88、1.89)，以及保持常数的诱导缩放(1.88、1.91)，都是李变换群的例子。从寻找偏微分方程组的解的角度上看，如果变换仅限于缩放，平移，或旋转，那李变换群的一般理论是不必要的。然而，事实证明还有更广泛类别的变换可以使偏微分方程保持不变。为了利用和发现这样的变换，李变换群的无穷小特性是至关重要的。

Sophus Li推出了用连续的变换群采用各种技巧来求解常微分方程的观念。他被他的朋友Norwegian Sylow关于Abel和Galois解代数方程组的演讲所激励。

李变换群的特点是无穷小生成元。Lie给出了一个来找出给定的微分方程所具备的点变换和更具一般的切变换的全部的无穷小生成元的算法。显著地，对于给定的微分方程而言，李变换群的基本应用仅仅只要求微分方程本身所拥有的无穷小算子的信息。

    一个点变换作用于一个微分方程的自变量与因变量所张成的空间上。李群的点变换自然地延伸到空间上，该空间中包括因变量的任何有限阶导数。出现在李变换群的无穷小生成元中的函数满足线性微分方程的超定组。点变换中的待定函数只有自变量与应变量，而切变换中的待定函数还包括一阶导数。一般来说，计算的方法，以及切变换的无穷小生成元的许多应用，扩展到高阶局部变换的无穷小生成元，其生成元中的函数允许取决于有限的较高阶导数。

由微分方程承认的李变换群相当于一种一个解对应同一微分方程另一个解的映射。有无数种方法表示这样的一种映射，可允许自变量任意变化的映射。如果自变量固定则表示方法是唯一的。当扩展李的算法来计算和使用微分方程承认的高阶局部变换，以及当扩展李的算法作用于一阶常微分方程到高阶常微分方程的积分因子，这种观点是必不可少的。

2.2李变换群

我们先从一个群的定义开始，接着考虑一个群的变换，更具体地考虑单参数李变换群。在这里，变换作用于实数Rⁿ。

2.2.1 群

  定义2.2.1-1 若在集合G上定义了运算Φ且集合G满足下面公理则称为群：

  (Ⅰ) 封闭性。a,bG，使得Φ(a,b)G。

  (Ⅱ) 结合性。a,b,c∈G，使得Φ(a,Φ(b,c))=Φ(Φ(a,b),c)。

  (Ⅲ) 有单位元。e∈G，对aG，使得Φ(a,e)=Φ(e,a)=a。

  (Ⅳ) 有逆元。aG，a^-1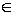G，使得Φ(a,a^-1)=Φ(a^-1,a)=e。

  定义2.2.1-2 若a,bG并且Φ(a,b)=Φ(b,a)，则集合G是阿贝尔群。

  定义2.2.1-3 G的子群是由G中拥有同一运算Φ的子集所组成的。