递归神经网络和有限自动机
H. T. Seigelmann
信息系统工程,工业工程与管理学院,理工,以色列,海法32000
目录
译文及原稿
摘要
关键词:递归神经网络 有限状态自动机 计算能力
1.引言
1.1.自动机
1.2.神经网络和有限自动机
我们表明,ρ-神经元形如
2.以往工作
3.模拟
4.主要结果
5.引理证明
致谢
参考文献
摘要
本文研究由同步进化的处理器相互连接构成的有限规模网络。每个处理器通过应用一个激活函数于所有单位的先前状态的一种线性组合来更新其状态。我们证明,任何存在左右极限且极限不等的函数能够被应用于神经元,来产生一个至少和有限自动机具有一样强大的计算能力的网络。我们推断,如果这就是所需要的能力,那么人们可以根据可用硬件或优先于特定应用程序的学习软件,来选择任何一个前述的神经元。
关键词:递归神经网络 有限状态自动机 计算能力
1.引言
递归神经网络能够逼近任意动力系统,这是在自适应控制和信号处理中运用的结果(Sontag 1992,Matthews 1992,Polycarpou和Ioannou 1991)。它们也构成了一组强大的计算模型(Siegelmann 1993)。在语音处理应用和语言归纳方面,递归网络模型被用作识别模型,且通过某些成本标准梯度下降优化的方法(所谓的“反向传播”技术)使其适应于实验数据(Cleeremans等 1989,Elman 1990,Giles等 1992,Pollack 1990,Williams and Zipser 1989)。
在这些网络中,根据在前一时刻某种类型的激活(xj)和输入(uj)的函数以及实系数——也被称为权重——(aij,bij,ci),更新每个处理器的激活。每个处理器的状态是通过以下所述类型的方程进行更新的。
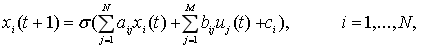 (1)
(1)
其中N是处理器的数量,M是外部输入信号的数量。函数σ被称为激活函数。递归神经网络的计算的和一般动力学的性质密切地取决于激活函数的选择。例如,如果σ是一个线性函数,那么该系统基本上是对一个初始矢量进行重复的矩阵乘法计算。如果,σ是Heaviside函数,且每个神经元取值于{0,1},那么系统变成有限状态。这些质的不同的行为激励了,关于在不同激活函数下的神经网络能力的研究。特别是,我们想知道各种(普及)的神经元能否构成一个足够强大的机器。为了这个目标,我们考虑到一种数学工具:一个自动机。
1.1.自动机
自动或时序机,是一个时间上演化,对外界刺激做出反应,并通过自身动作来依次影响它的环境的装置。在计算机科学和逻辑学中,自动机理论涉及了这个概念的各种形式化。在这种正式的意义上,神经网络构成了一个(非常)特殊类型的自动机。因此,通过在计算机科学上被研究的经典自动机的更抽象的一般模型与它们的比较,分析神经网络的信息处理与计算能力是自然的。这给出在明确数学术语中,神经系统能力的描述。
实际自动机的部件可以采取多种物理形式,如在机械设备上的齿轮,机电的那些继电器,以及在现代数字计算机的集成电路,或神经元。这样一个对象的行为将取决于适用的物理原理。然而,从自动机理论的角度看,所有这些都是相关的,是一组内部状态的识别,该内部状态在给定的一个时刻描述了设备的状态,连同在当前状态和从外界输入的基础上预测下一状态的操作规则的特化。用于产生输出信号的规则也可以被纳入该模型。
虽然自动机的数学形式化发生在数字计算机出现之前,但为了解释基本原则,把计算机作为一个自动机的范例是非常有用的。在这个范例中,在一个给定的时间t,一个自动机的状态,对应于所有RAM内存地址中完整的内容,



