行星齿轮固有频率
摘要
在行星齿轮的应用中为了减少噪音和振动的,主要设计参数往往是不同的,以避免共振,优化负荷分配,降低重量。在固有频率与行星齿轮参数对比的图表中,当两个特征值的轨迹彼此接近时出现转向,但后来突然转向了。转向的重要性体现在固有频率的改变和由此产生的响应影响的急剧的变化上。这个工作分析行星齿轮特征值转向规则的特点.通过扰动分析得到两个靠近的固有值轨迹的耦合系数是接近的。特别的转向模式是通过使用独特性能的行星齿轮振动方式获得的。 这个结果通过一个例子说明。对关键设计参数进行研究,概括性推广是为行星齿轮固有频率的调整做准备。
导言
减振降噪对于行星齿轮的应用至关重要。在设计过程中,系统参数是多种多样的,以评估比较设计选择,避免共振,优化负荷分配,降低重量。它的特点有非常重要的影响对固有频率和振动方式的参数变化的有效调整。在行星齿轮动态模型(图1) ,主要设计参数包括啮合刚度,支座/轴承刚度,部件质量,转动惯量。一些固有频率的图表与行星齿轮参数由Cunliffe等人 [1],Botman [2], Kahraman [3,4],and Saada and Velex [5]提供。
固有频率特性曲线在这些研究中,特别是编号3,显示固有

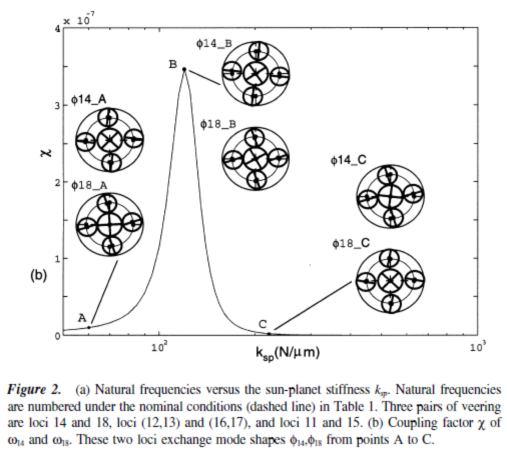
频率转向现象在当两个相互靠近的固有频率轨迹作为一个参数时是多种多样的,但后来突然转向就像两个电荷相互排斥(B点的图2A)。振动模式转向特征值在临近转向时进行了关联性强且急剧的变化。这一现象已被广泛的研究[6-9] ,但在行星齿轮中还没有被研究过。特征值转向也与模式定位有联系,就会发生名义上对称系统的混乱引入,如涡轮叶片,空间天线,多跨梁,和其他结构[6] 。在特别的情况下急剧转向,有时通过固有值轨迹图很难区分转向和交叉。曲线转向/交叉严重妨碍在特征参数变化时的固有值轨迹的描图。此外,当多个曲线转向或交叉紧密时(图3),强大的模态耦合及相关的操作条件发生变化的反应在特性曲线图中是无法识别的。
这项工作的目标是双重的。首先是简单的分析预测行星齿轮固有值转向的简单规律。第二是利用转向结果,连同以前制定模态特性和特征值分析,以确定自由振动模型参数更全面的影响,,并在调整固有频率时给予指导。Lin and Parker [10,11]分析了高度结构化的特性行星齿轮固有频率谱和振动模式独特特点。他们还提供了简单,封闭形式表达式来表达固有频率和振动模式设计参数的灵敏度[12] 。这些分析结果提供必要的基础研究行星齿轮转向规则。转向规则产生具体的结论可以在简单的表格表达两个特征值转向接近或交叉。转向规则的重要性是查明那些在小范围内的变化设计参数,可大大改变振动模式和相应结果。结论由在一个基准行星齿轮(模型参数和自然频率给出了表1和表2 )中使用的直升机动力传动系统说明。
来自参考10的集总参数模型用在这里。该模型适用于有N行星的一般行星齿轮。每个组成部分都有两个平移和一个旋转自由度(自由度)在平面运动中,因此该系统具有L = 3(N + 3) 个自由度。在这种情况下固定配置和L = 3(N + 2)可以用数学公式表达。有关特征值问题是
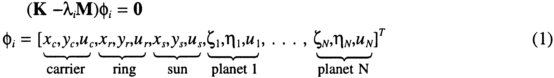



二.转向/交叉准则
在一般动态系统上检测特征值转向/交叉的方法介绍。图2AB点就是一个转向例子。当有两个特征值轨迹相互远离时,他们的轨迹曲率显示曲线方向有突然的变化。Perkins 和 Mote [7]提出了转向/交叉标准俩估计在临近转向去的轨迹曲率的独特特征。让λr和λs做为两个特征值围绕B点接近对方作为一个参数r是多种多样的。在B处特征值不受干扰的是(λr,Φr) 和 (λs,Φs)。在B处应用泰勒展开,位点的特征值近似
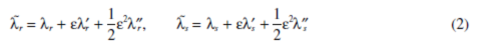
å是一个小扰动可变参数。λ¢=¶λ/¶r;λ¢¢=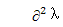
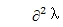 。二阶导数λ¢¢r andλ¢¢s 用来描述轨迹曲线。假如λ¢¢r = λ¢¢s = 0,两个轨迹是独立且自由的相互交叉。假如λ¢¢r , λ¢¢s ¹0,轨迹交叉且转向发生。作为一个特殊的特征值,特征值二阶导数是
。二阶导数λ¢¢r andλ¢¢s 用来描述轨迹曲线。假如λ¢¢r = λ¢¢s = 0,两个轨迹是独立且自由的相互交叉。假如λ¢¢r , λ¢¢s ¹0,轨迹交叉且转向发生。作为一个特殊的特征值,特征值二阶导数是
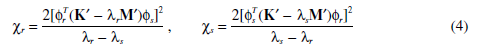
在临近转向是当λr≈λs时λ¢¢r andλ¢¢s被一个小分母限制,那是

耦合系数cr和cs 近似局部曲率。它们被用于估计转向强度。
2b图显示c = c14 = -c18转向轨迹w14和w18在图2a中的可变参数ksp。注意图2b急剧变化的振动模式。这两个转向位点交换模式从点A至C ,即使轨迹不相交。这个模式在B点有很强的联系性且不像任何在转向区外的转向模式。在转向区当参数调整,振动模式的急剧变化可以对工况动态响应,齿轮负载,负载分配,轴承强度产生巨大影响而且可能导致模态局部化。在何种程度上个体模式的动态啮合力(即模态力)也变化急剧作为转向改变模。
转向准则可以应用在当λs=…=λs+m-1退化多个m时。特征值二阶导数是
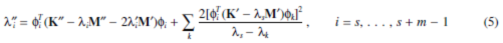
当指数总和k=1,…L,但k ¹s,…, s+m -1。当另一个特殊特征值λr接近λi,这个主项在公式5和3中时
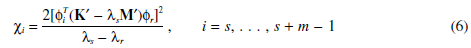

假如λr=…λr+n-1也去掉,耦合系数是


假如耦合系数全为零,λr和λs轨迹重合,否则转向发生。下面是检验条件
三.行星齿轮转向模型
当适用于行星(或任何行星)齿轮,上述结果归纳为特别简单的形式,因为独特的结构振动模式。所有行星齿轮振动模式可在假设下的循环对称行星之间分为以下类型[10] 。分析仅限于本常用的行星齿轮。
1.有特殊固有频率的六旋转方式。它们有绝对旋转的轴,环和恒星轮。xh = yh = 0, h = c, r, s。所有的行星轮有相同的挠度
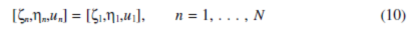
2 六对平移模式缺少两个固有频率。它们有绝对平移的轴,环和恒星轮。uh = 0, h = c, r, s,作为一对标准正交的平移模式Φi 和 Φj (
 MΦj = 0),
MΦj = 0),
 ,上标i和j各自表示Φi 和 Φj。行星挠度存在联系
,上标i和j各自表示Φi 和 Φj。行星挠度存在联系
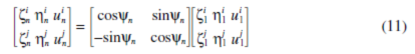
当行星轮相同时Yn=2(n-1)
 /N
/N
3.三个成组的行星轮模式其中缺少N-3个固有频率。他们有不动的轴,环和恒星轮,xh= yh =uh= 0, h=c,r, s,行星挠度关系式
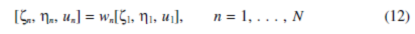
wn是N-3的独立标量满足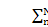
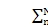 nsinYn
nsinYn
 ,
,
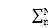 ncosYn
ncosYn
 ,
,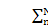
 n=0
n=0
两个接近行星齿轮轨迹可以与任何上述三种类型的模式有关。这特殊的模型如公式10-12可以用于分析行星轮转向。具体来说,让恒星行星啮合刚度ksp是可变参数(图1)和M¢=0。
案例1.两个旋转模式轨迹λr和λs 。转动方式有不同的特征值,ksp二阶导数是[ 12 ]

当dsn=yscos(Yn-as)-xssin(Yn-as)-hncosas-znsinas+us+un是第n个恒星行星啮合刚度动态描述模式挠度。as是恒星行星啮合的啮合角;上标r和k在指示振动方式jr和jk。第n个恒星行星啮合的应变能是d¢sn = ksp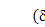
 /2。转动模式公式10是
/2。转动模式公式10是
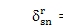 ,
,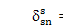
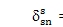 公式4的耦合系数是公式13的主项
公式4的耦合系数是公式13的主项
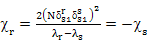
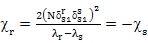 (14)
(14)
假如
 ,
,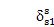
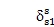 且cr, cs
且cr, cs
 0,接近的特征值轨迹转向远离,假如
0,接近的特征值轨迹转向远离,假如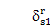
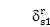 or
or
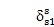 , then cr=cs=0且cr=cs=0,轨迹彼此交叉。这要求振动方式
, then cr=cs=0且cr=cs=0,轨迹彼此交叉。这要求振动方式
 r 或js所有恒星行星啮合的应变能Usn=0。可是,所有的转动方式除了缸体模式有应变能在恒星行星啮合中。因此两个转动模式的轨迹(例如w14 和 w18在图2a)总是远离且不交叉。同样的更多的应变能在恒星行星啮合意味着大量cr 和 cs和剧烈的转向。双方轨迹有相同的曲率,则cr-cs;
r 或js所有恒星行星啮合的应变能Usn=0。可是,所有的转动方式除了缸体模式有应变能在恒星行星啮合中。因此两个转动模式的轨迹(例如w14 和 w18在图2a)总是远离且不交叉。同样的更多的应变能在恒星行星啮合意味着大量cr 和 cs和剧烈的转向。双方轨迹有相同的曲率,则cr-cs;
转向行星齿轮等同起来的耦合因素,零利率的条件,没有曲线转向;这个是典型的结论。
案例2.两个平移模式的轨迹λr=λp且λs=λq。减轻重量例5平移模式模型,导数λ¢¢r 和λ¢¢p和公式13有相同的形式,除了指数和k=1,… ,L, but k¹r, p。公式8和公式9的耦合系数是λ¢¢主项:


公式11的平移模式性质导出此项关系
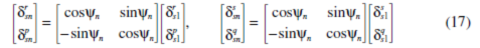
运用公式17,15和16得到
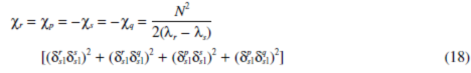
耦合系数等于零(轨迹交叉)要求
 or
or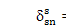
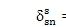 = 0,对于所有的n。总的说来,这意味着平移模式副(jr,jp) 和 (js,jq)的恒星行星啮合没有任何应变能。这不会发生,且轨迹总是远离由cr 和 cs决定 (图2a例 w12,13 和 w16,17 )。
= 0,对于所有的n。总的说来,这意味着平移模式副(jr,jp) 和 (js,jq)的恒星行星啮合没有任何应变能。这不会发生,且轨迹总是远离由cr 和 cs决定 (图2a例 w12,13 和 w16,17 )。
案例3.转动模式轨迹λr和平移模式轨迹λs,λq,由公式6和7得,耦合系数是

上述
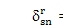 和 公式 17, cs=q=cr=0 是自然满足的因为
和 公式 17, cs=q=cr=0 是自然满足的因为
 Yn
Yn
 ,
,
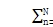 Yn
Yn
 0。此处对任意dsn没有任何条件限制,这不同于以上例子。一个转动模式的轨迹与一对没有转向的平移模式的轨迹交叉。通过类似分析,行星模式轨迹总是与转动和平移模式的轨迹交叉。
0。此处对任意dsn没有任何条件限制,这不同于以上例子。一个转动模式的轨迹与一对没有转向的平移模式的轨迹交叉。通过类似分析,行星模式轨迹总是与转动和平移模式的轨迹交叉。
案例4.两个行星模式的轨迹λr…λr+m-1 和
 s=…=λsm-1,当m=3(N-3)时。λr, …, λr+m+1的二次导数与公式13有一样的形式,除了指数总和k=1,…, L, 但 k¹r,…,r+m-1。公式8和9的耦合系数是
s=…=λsm-1,当m=3(N-3)时。λr, …, λr+m+1的二次导数与公式13有一样的形式,除了指数总和k=1,…, L, 但 k¹r,…,r+m-1。公式8和9的耦合系数是

那些耦合系数都为零导出不发生转向的条件

利用公式12的行星模式模型,恒星行星啮合变形与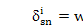
 和
和 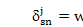
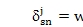 有联系。公式22导出
有联系。公式22导出
 0,i= r,…,r+ m -1 且
0,i= r,…,r+ m -1 且 
 0= 0, j=s,…,s++ m-1,总体来说,这些条件要求一对退化振荡模在恒星行星啮合中没有应变能。这大体上不会发生,因此两个行星模式的耦合系数不为零,且他们的轨迹转向远离(图2aw11 和w15),特殊讨论的除外。
0= 0, j=s,…,s++ m-1,总体来说,这些条件要求一对退化振荡模在恒星行星啮合中没有应变能。这大体上不会发生,因此两个行星模式的耦合系数不为零,且他们的轨迹转向远离(图2aw11 和w15),特殊讨论的除外。
案例5。两个减弱行星模式轨迹相互接近时,kp,mp或Ip是各种各样的此金伯利进程,这个例子当ksp=krp且压力角ar=as= a时,三个行星模式有额外的模型除了公式 12 ,并且可进一步划分为如下[ 10 ] :模式P1只有行星轮切向运动hn (zn=un=0);(2)模式P2没有切向运动(hn = 0)而且径向运动占支配地位(zn=un) ;(3)模式P3没有切线运动(zn =un);而且行星旋转占支配地位(hn=0),行星模式P1从P2和P3减弱得来。假如压力角a=0P2和P3也会减弱,也就是说,P2中un= 0和P3中 zn=0 。由于这些附加的模型两个减弱的行星模式轨迹能相交。例如,kp作为一个可变参数。一个行星退化振荡模的特征值λr…,λr+m-1的二阶导数是
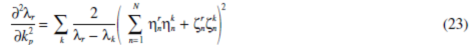
当指数总和k=1,…, L, 但 k ¹r,…, r+m-1时耦合因数是
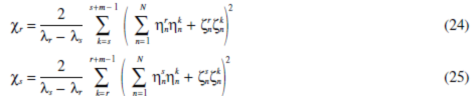
|
假如λr是模式P1,λs 是模式P2或P3, 保证cr= cs=0,因为   = 0, i=r, … , r+m-1 且 = 0, i=r, … , r+m-1 且   =0,j=s,…, s++ m -1。所以模式P1的轨迹与P2和P3的轨迹交叉(例图3 ,w11 和 w15交叉在ksp=krp,ar= as时)。可是P2和P3模式轨迹转(图3,w5 和 w15)向远离,因为它们在a¹0时相连。假如条件ksp=krp和ar=as不满足,三个耦合行星振型转向远离如同案例4中所讨论的一样。 =0,j=s,…, s++ m -1。所以模式P1的轨迹与P2和P3的轨迹交叉(例图3 ,w11 和 w15交叉在ksp=krp,ar= as时)。可是P2和P3模式轨迹转(图3,w5 和 w15)向远离,因为它们在a¹0时相连。假如条件ksp=krp和ar=as不满足,三个耦合行星振型转向远离如同案例4中所讨论的一样。
上述分析(例1-4 )使用ksp作为变参数和显示两个相同的模式的特征值轨迹转向远离和两个不同的模式类型相互交叉。这种模式通常是有效的,其他参数(或刚度或惯性)是多种多样的。改变刚度(ksp, krp, kp, kh, khu, h= c,r,s),在动态描述刚度时特征值导数与挠度 d 相关[12]。如果两个轨迹有相同的模式类型,如在案件1,2和4中,耦合因子c =0总是要求在相应的振动模式中挠度d= 0。这一要求是不可能得到满足,除非特殊情况的讨论情况
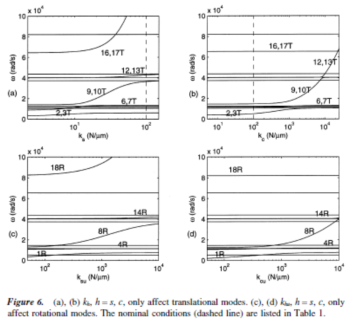
因此c¹0适用于两个同一类型轨迹靠近和转向发生。如果两个轨迹属于不同的类型,模式的情况如同案例3,c= 0自动满足由于模式模型公式10-12,轨迹一直交叉。对于变换惯量(mh,Ih,h= c,r,s,p),分析是类似的刚度。一般转向/交叉模型的摘要列于表3和很明显的例子如图4。改变惯性(其中参数不同于图2) 。
四.应用
该转向模式有助于追查的特征值轨迹的演变,并确定设计参数对行星齿轮振动的影响。行星齿轮传动系的直升机是用来作为一个例子。名义模型参数见表1表2列出了模式及类型占主导地位的应变能在每一个模式。固有频率的编号的名义条件(所显示的虚线在图2-7 )。
啮合刚度ksp和krp (图2和5 )没有多大的影响力对低
|
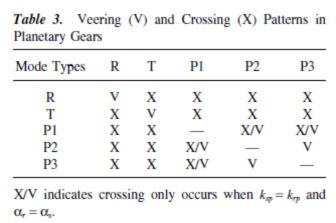

固有频率w1~w10。这是因为,这些模式是由轴承刚度支撑(表2)那些远小于啮合刚度。15-18模式有很大的应变能在恒星行星啮合和受ksp(见图2 )影响 ;模式11-14有大量应变能在环行星啮合和受krp (图5 )影响。当ksp从公称值减少,w15 -w18变化接近 
 11 -w14的轨迹。由于同一类型的轨迹不能相交,转向发生转动模式18和14间,平移模式对(16,17) 和(12,13),行星模式15和11.在转向区以下(ksp=100N/mm),模式11到14非常接近在转向区之上的模式15至18 (ksp=800N/mm)。以同样的方式,人们可以预测的固有频率krp增长时轨迹趋势(见图5 )。支撑刚度kh, khu,和轴,环,恒星轮的h=c, r, s,分别可以随各种不同的配置(固定或浮动这些组件)。旋转和行星模式是完全独立于横向刚度Kh,因为他们没有平移轴,环和恒星轮只有平移模式受到变化的Kh影响(图6A,6b)。当转动支座刚度khu改变,类似的结果(图6c,6d),除非它是旋转模式,很容易受到khu的变化影响。
11 -w14的轨迹。由于同一类型的轨迹不能相交,转向发生转动模式18和14间,平移模式对(16,17) 和(12,13),行星模式15和11.在转向区以下(ksp=100N/mm),模式11到14非常接近在转向区之上的模式15至18 (ksp=800N/mm)。以同样的方式,人们可以预测的固有频率krp增长时轨迹趋势(见图5 )。支撑刚度kh, khu,和轴,环,恒星轮的h=c, r, s,分别可以随各种不同的配置(固定或浮动这些组件)。旋转和行星模式是完全独立于横向刚度Kh,因为他们没有平移轴,环和恒星轮只有平移模式受到变化的Kh影响(图6A,6b)。当转动支座刚度khu改变,类似的结果(图6c,6d),除非它是旋转模式,很容易受到khu的变化影响。
改变行星轮参数影响固有频率就像所有模式一般包括行星挠度。运用转向结果得到,五对转向被确定为行星轴承刚度变化如图3 :旋转模式8,18,4和14;平移模式( 9,10 )和(16,17),(6,7)和(12,13);和行星模式5和15对于大刚度kp=5000N/mm,8固有频率迅速增加,超出影响范围以外.行星轮质量mp和转动惯量Ip也对固有频率有重大影响(图7 ) 。

五.讨论及结论
行星轮在行星齿轮应用可以不等间隔。行星齿轮的行星相位角度 Yn满足
 Yn
Yn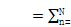
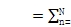 Yn
Yn
 0 ,振动模式保留结构性能[ 11 ]:6独特的旋转方式,12个独特的平移模式和3个行星模式有多重N-3。平移模式成为独特的,因为损失循环对称。在这种情况下,转向模型如表3仍然适用,但轨迹曲率的分析有一个更复杂的形式。一个重要案件有几乎截然相反的行星相位的角度
0 ,振动模式保留结构性能[ 11 ]:6独特的旋转方式,12个独特的平移模式和3个行星模式有多重N-3。平移模式成为独特的,因为损失循环对称。在这种情况下,转向模型如表3仍然适用,但轨迹曲率的分析有一个更复杂的形式。一个重要案件有几乎截然相反的行星相位的角度 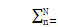
 Yn
Yn
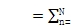 Yn
Yn
 0。图8显示一个四行星例Yn= 0,82,169,262,
0。图8显示一个四行星例Yn= 0,82,169,262,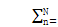
 Yn
Yn
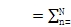 Yn
Yn
 0,而其他参数保持不变。平移模式第9和第10,这是平等的星球退化间距,与转动模式8交叉,但转向远离平移模式16,17
0,而其他参数保持不变。平移模式第9和第10,这是平等的星球退化间距,与转动模式8交叉,但转向远离平移模式16,17

间隔任意,公式10-12振动模式失去结构性能,所以得出的转向模式是无效的。
固有值轨迹转向也会发生当退化模式系统被一个小干扰分开时。在行星齿轮中,循环对称性可以打破由于不同的行星啮合啮合,制造业的变化,以及装配错误。对于周期性对称或定期系统由于小干扰,弱结构耦合模式,模式定位,往往伴随着固有值轨迹转向[ 6 ] 。行星齿轮有相对坚固的耦合当行星轮之间通过轴和齿形啮合时,因此大幅模式定位是不可能即使存在轨迹转向。经过
审查各种配置和参数,我们还没有找到一个行星齿轮模式定位的现实的例子。
特殊转向模式行星齿轮特征基因很容易总结。同一类型两个接近的特征值轨迹(旋转模式,平移模式,行星模式)转向了,而两个不同的模式类型的轨迹相互交叉。这种模式振型在通过转向区时交换。在转向区,耦合模式坚固而且与区域有显着不同。但可以预见的显着性差异响应这些变化模式。这些规则产生的独特的模态性能的行星齿轮和适用于所有的设计参数。转向模式的特点,再加上独特的模态特性和固有值分析,可以深入了解行星齿轮自由振动。
关键设计参数的影响概括如下:
1 .啮合刚度。ksp和krp控制三个不同的固有频率与一个旋转模式,一双转化模式,一组行星模式。在这些振动模式的齿形啮合中应变能占支配地位。
2.轴,环和恒星参数kh, khu, h=c,r,s,每个只影响一个固有频率。横向刚度Kh控制一双平移模式,扭转刚度khu控制一个旋转模式。浮动或固定轴,环,或恒星轮对行星齿轮模态属性有一定影响。轴,环,或恒星轮质量和转动惯量影响同一频率,相应的支座刚度,虽然频率变化有相反的方向。
3 .行星轮参数。行星轴承刚度和行星惯性是最有影响力的参数和影响大多数固有频率。一个硬的行星轴承,可以有利于共振调整,因为它大大降低了一些在较低的频率范围的固有频率。



